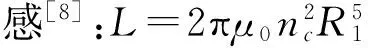散热通道式线圈电感分析与计算*

逯博文，邱望标，潘　振，陈伟兴

(贵州大学机械工程学院，贵州贵阳550025)



散热通道式线圈电感分析与计算*

逯博文，邱望标，潘振，陈伟兴

(贵州大学机械工程学院，贵州贵阳550025)

摘要：针对工程应用中线圈长期工作散热困难现象,设计了一种有利于散热的新型通道式线圈；为解决常规方法无法求解新型线圈电感值问题，提出了一种计算新型线圈电感的方法，将线圈尺寸转换为当量尺寸，转化后的线圈起名为等效线圈，并利用矢量磁场的方法求出线圈的电感，所求数值与实际测量值相吻合，为线圈在工程中的应用打下基础。

关键词：散热通道等效当量线圈当量尺寸矢量磁场

0引言

国内外应用线圈产生的磁场做磁处理时都是层层密绕，线圈层与层之间的热量不易被释放，大多使用风扇进行散热处理，线圈层与层之间的空气无法流通，若长期工作，热量积累易导致线圈损坏，故不能应用到实际工程中。为解决线圈散热困难问题，设计了一种新型绕线方式的散热通道式线圈，加快了线圈层与层之间热量的释放，突破了传统线圈绕线形式的局限。

1散热通道式线圈结构设计

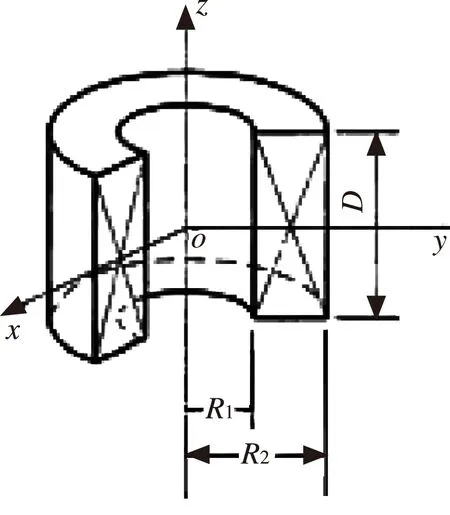
新型散热通道式线圈结构设计如图1所示，绕线体的断面有通气孔和竹签孔，竹签穿过整个腔体以支撑线圈，使得线圈之间留有空气通道，以达到散热的目的，竹签按照圆形排布在腔体内，每层竹签绕两层线圈，线圈产生的热量通过竹签间的散热通道从端面的通气孔排出，此时热量储存在端面夹层之间；端面夹层之间的柱面上有排气孔(图2)，热量通过排气孔排入大气以解决线圈长期工作散热问题。

图1　侧面剖视图　　　　　　图2　轴测剖视图

2空心圆柱线圈的电感分析

线圈由细导线密绕而成，设通电电流I，线圈总匝数W,匝流密度即安匝每米是NC,线圈绕线区域所占空间为V′，截面面积为s0。

则第m匝导线所匝链磁链[1]为：

ψm=∫SmB·dS

=∮lmA·dl

(1)

式中：B—通电线圈产生的磁通密度；

Sm—线圈第m匝导线所围成曲面；

lm—线圈第m匝导线所围成曲面的边界。

由式(1)可写出线圈所匝链总磁链[2]：

(2)

JC是线圈电流密度。式(2)变为：

(3)

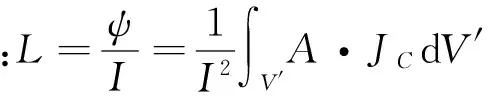
(4)

通电空心圆柱线圈矢量磁位有周向分量Aφ,在任意点(ρ，φ，z)处矢量磁位A和电流密度JC同方向，所以：

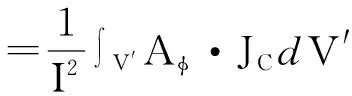
(5)

整理得到：

A1-2=A′+A″

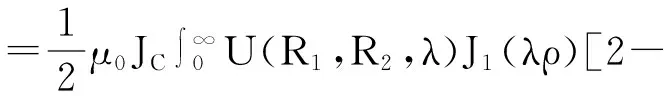
(6)

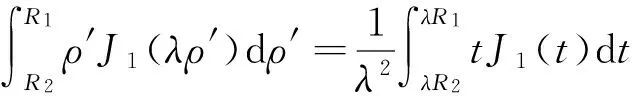
=λU(R1，R2，λ)[3]

其中令t=λρ′

(7)

利用JC=ncI得：[4]

(8)

以线圈内半径R1为基准把线圈各个长度量归一化，令：

工作时调速电机通过链传动带动轴旋转，轴通过支撑轮带动滚筒旋转。在旋转过程中，滑板受到凸轮槽的限位作用，在滚筒及支撑轮组成的滑道内上下运动。凸轮槽结构如图2所示。

其中p和q称为形状参数，则：

(9)

比照U(R1，R2，λ)的定义令：

(10)

(11)

利用以上结果,式(8)转化成

(12)

式中：

(13)

式(12)是所求空心圆柱线圈自感解析的表达式。

函数T(q，p)的计算应用图表法，对应如表1[6]。

1)函数表最左一列为形状参数q,最上一行为形状参数p。

2)函数表T值最大绝对误差是5×10-5。

3)当所给形状参数在函数表中没有对应T值时,使用下面的插值公式计算可得到所需T值[7]。

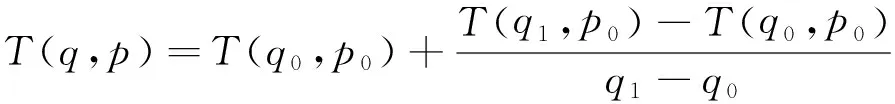
(14)

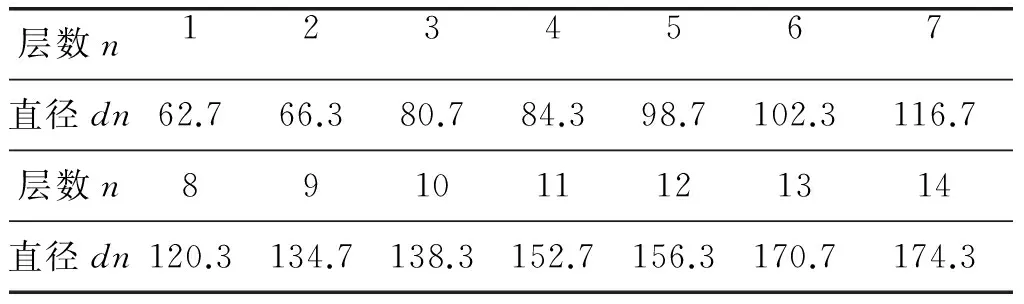
式中，q和p为待求函数T所对应形状参数,q0

表1　q、p相邻形状参数

3等效当量线圈尺寸的确定及电感计算

由线圈支撑结构尺寸得知线圈共绕14层，每两层之间用竹签隔开(图3)，线圈缠绕长度为300 mm,导线直径为1.7 mm，经计算确定每层导线的缠绕直径如表2所示。

表2　线圈各层绕线长度

经计算缠绕线圈总长度：

图3　等效当量线圈

实际密绕至18层时接近计算长度，故当量层数为18层，此时散热通道式线圈当量截面积当量外径R2为125.8 mm，当量内径R162.7 mm(图3)，当量匝数3 176匝，q=D/R1=4.78，p=R2/R=2，查表1得出相邻形状参数，根据公式(14)计算得T=3.26。

参考文献

[1]盛剑霓.工程电磁场数值分析[M].西安:西安交通大学出版社,1991.

[2]Witkowski L M, Marty P, Walker J S. Multidomain analytical-numerical solution for a rotation magnetic field with a finite-length conducting cylinder. IEEE Transactions on Magnetics,2000,36(2):452-460.

[3]陈乔夫,李湘生.空心电抗器的电感计算[J].华中理工大学学报,1994,22(4):11-15.

[4]王昕,王宗欣,袁晓军.圆形螺旋线圈自感和分布电容的计算[J].固体电子学研究和进展,2000,20(4):424-432.

[5]卡兰塔罗夫.采伊特林.电感计算手册[M].陈汤铭，等译.北京:机械工业出版社,1992:263-279.

[6]张善杰,唐汉，等.实用计算方法[M].南京:南京大学出版社,1998.

[7]丁斌，杨宁，王志萍．电感线圈分布电容和谐振频率的仿真与测量[J]．变压器，2010，47(9): 41-43．

[8]齐立荣,李海波,朱义胜.平面螺旋电感参数的计算和仿真研究[J].林区教学,2007(2)57-58.

中图分类号：TB131;TH123+.1

文献标识码：A

文章编号：1002-6886(2016)03-0030-03

基金项目：贵州省科学技术基金(黔科合J字LKS[2013]42号)。

作者简介：逯博文(1991-)，男，硕士研究生，研究方向：机电工程。

收稿日期：2016-03-16

Analysis and calculation of the inductance of the coil with cooling channels

LU Bowen, QIU Wangbiao, PAN Zhen, CHEN Weixing

Abstract:To solve the problem of difficulty in cooling of coils in long-term operation, we designed a new type of coil with cooling channels. Since the conventional method can’t calculate the inductance of the new coil, we introduced a new method to calculate its inductance. We converted the coil size into an equivalent size, and named the converted coil an “equivalent coil”. Then vector magnetic field was applied to calculate the inductance of the coil. The results were in correspondence with the measured data. This study laid the foundation of the engineering application of the coil.

Keywords:cooling channel; equivalent coil; equivalent size; vector magnetic field