大气隙混合磁悬浮轴承-转子系统耦合特性仿真分析

任茂发，郑　好，李博宇

(武汉理工大学机电工程学院，湖北武汉430070)



大气隙混合磁悬浮轴承-转子系统耦合特性仿真分析

任茂发，郑好，李博宇

(武汉理工大学机电工程学院，湖北武汉430070)

摘要：磁悬浮支承技术是利用可控电磁力使物体沿着一个方向或几个方向保持一定位置，从而使物体与基础之间无机械接触，根据磁力轴承工作原理，磁悬浮转子在实际工作时，在结构和控制系统中存在着多种耦合现象。介绍了大气隙混合磁悬浮轴承的结构以及这种轴承的工作特点与工作原理；建立其等效磁路模型；针对大气隙混合磁悬浮轴承结构，利用有限元软件分析其磁场耦合特性，以偏心距为变量，分析大气隙混合磁悬浮轴承-转子系统的力耦合与力矩耦合。结果表明：偏心距越大，耦合越强。

关键词:大气隙混合磁悬浮轴承耦合特性仿真

0引言

磁悬浮支承技术是利用可控电磁力使物体沿着一个方向或几个方向保持一定位置，从而使物体与基础之间无机械接触，它是集电磁学、控制工程、电子技术、信号处理、动力学、机械学为一体的典型的机电一体化技术[1]。

根据磁力轴承工作原理，磁悬浮转子在实际工作时，在结构和控制系统中存在着多种耦合现象。例如磁极之间的磁耦合、径向磁力轴承横截面内两个相互垂直方向的力耦合、转子前后径向磁力轴承之间的力矩耦合、径向磁力轴承与轴向磁力轴承的力矩耦合、位移传感器间的信号耦合、转矩耦合、控制与结构的耦合等[2]。混合磁悬浮轴承中的磁场是由电磁磁场和永磁磁场组成，存在电磁磁场和永磁磁场之间的磁耦合，力耦合以及运动耦合；大气隙条件下的磁悬浮轴承漏磁严重，磁场分布不均匀，所以，对其耦合特性关系的研究十分重要，不仅对寻求解决耦合的方法有重要作用，还为其控制系统设计提供重要参考。

本文针对大气隙混合磁悬浮轴承结构，利用有限元模型分析其磁场耦合特性，以偏心距为改变参数，分析大气隙混合磁悬浮轴承-转子系统的力耦合与力矩耦合。总结大气隙混合磁悬浮轴承-转子系统耦合特性规律。

1大气隙混合磁悬浮轴承结构及等效磁路模型[3-4]

1.1混合磁悬浮轴承的工作原理

永磁磁通和电磁磁通共同组成混合磁悬浮轴承的磁通系统，永磁磁通和电磁磁通一般情况下都有各自的磁通源和磁路，两种磁场最后在混合磁悬浮轴承工作气隙中叠加形成混合磁场，利用混合磁场实现转子的悬浮支承。

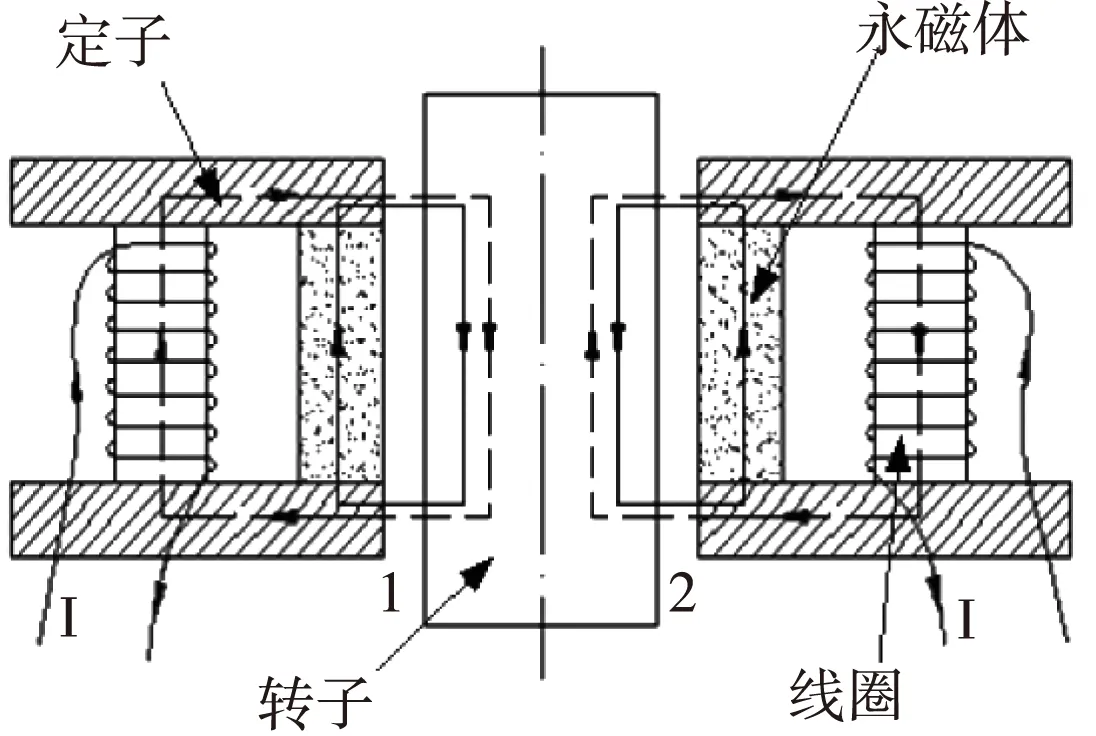
图1　混合磁悬浮轴承工作原理图

如图1所示，电磁极产生的主动磁通由虚线表示，永磁极产生的偏置磁通由实线表示。

由结构的对称性可知，每个永磁极长度相同，即气隙1与气隙2的长度相等，则永磁极产生的静态偏置磁通相等(设对应的磁通为φ1和φ2，磁力为F1与F2)即φ1=φ2，偏置磁通产生的电磁力相等，即F1=F2，在不考虑重力的情况下，电磁极不通电时，则系统所受合力为0，系统处于平衡状态。

假设，在转子处于平衡状态时，受到一个向左的扰动，转子将偏离平衡位置，向左产生一定的位移。此时，左边气隙减小，右边气隙增大，所对应的磁通将发生改变，即φ1>φ2，此时，所对应的磁场力也会随之发生改变，即F1>F2。转子将在磁场力的作用下，继续向左运动。与此同时，位移传感器将检测到位移偏移信号，将此信号传输给控制器，控制器将位移信号转换成控制信号，并将此控制信号输送给功放，功放将此控制信号转换成电流信号，此时，即电磁极通电，则电磁极产生对应的控制磁通(设为φk)，在气隙1处，电磁磁通和永磁磁通方向相反，相互削弱，使得左边的磁通变为φ1-φk，电磁力减小；在气隙2处，电磁磁通和永磁磁通方向相同，相互叠加，使得右边的磁通变为φ2+φk，电磁力增大；最后使得左右电磁力相等，使转子处于平衡位置，同理，由结构的对称性可知，受到其他方向的扰动时，系统有相同的工作过程。

1.2大气隙混合磁悬浮轴承结构及等效磁路模型

根据文献[2]，可采用气隙-定子内径比值k来界定普通气隙与大气隙混合磁悬浮轴承。当k≥0.02时，可看作大气隙混合磁悬浮轴承。本文研究的混合磁悬浮轴承的k=0.05(气隙为3mm，定子内径60mm)，满足大气隙混合磁悬浮轴承的定义。

图2　大气隙混合磁悬浮轴承结构图

如图2所示，大气隙混合磁悬浮轴承由永磁体、定子铁芯、永磁体极靴、线圈、转子铁芯构成。定子铁芯包括4个电磁磁极与4个永磁磁极，径向8极均匀分布，电磁磁极与永磁磁极相间布置。4个永磁磁极径向充磁，永磁回路由永磁磁极与相邻的电磁磁极构成。电磁磁极沿水平和垂直方向布置，分别形成Y通道与X通道的电磁控制磁通。

图3所示大气隙混合磁力轴承的等效磁路，图中实线表示偏置磁通(又叫永磁磁通)，由永磁磁极提供，其路径为永磁体-气隙-转子-气隙-电磁磁极；虚线表示控制磁通(又叫电磁磁通)，由电磁磁极提供，其路径为电磁极-气隙-转子。由图3可知，Y通道方向上气隙处偏置磁通与控制磁通相互叠加，下气隙处偏置磁通与控制磁通相互抵消，混合磁悬浮轴承在Y方向形成差动控制使转子稳定悬浮。

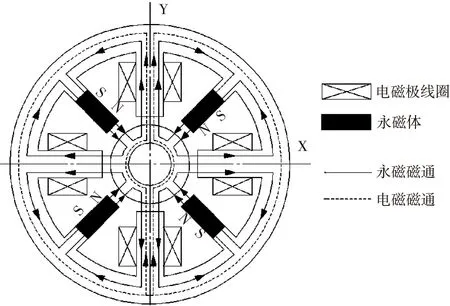
图3　大气隙混合磁悬浮轴承磁路图

2大气隙混合磁悬浮轴承-转子系统耦合特性仿真分析[5-9]

2.1永磁磁通磁场分析

图4　大气隙混合磁悬浮轴承三维模型网格划分图

使用有限元软件ANSYS work bench11.0建立了大气隙混合磁悬浮轴承的三维模型，分析磁力线分布，磁感应强度分布，其三维模型网格划分如图4。

图5所示为转子处于平衡，不通控制电流，仅有永磁偏置磁通的条件下，大气隙混合磁悬浮轴承的磁感应强度分布情况。图中不同的颜色，代表着不同大小的磁感应强度。

图6所示为转子处于平衡，不通控制电流，仅有永磁偏置磁通的条件下，大气隙混合磁悬浮轴承的磁力线分布情况。

由图5与图6可知，当转子处于平衡，不通控制电流，仅有永磁偏置磁通的条件下，磁场对称均匀分布，并且在永磁极处磁感应强度最大，在各电磁极处大小相等，且比永磁极处的磁场强度小很多，漏磁较为严重，但耦合现象不明显。

2.2大气隙混合磁场以X、Y方向的偏移量为变量，混合磁悬浮轴承-转子系统力耦合分析

现以X、Y 方向的偏移量为变量，来讨论两大气隙混合磁力轴承之间电磁耦合特性，即当转子X、Y 方向电流为一定值时，研究x0、y0对大气隙混合磁悬浮轴承承载力Fy的影响。

为确保Y方向磁力有一定大小同时消除X方向电流的影响，保证仅受单一要素影响，取ix=0，iy分别为1A、3A与5A，X方向偏移为-1.2mm～1.2mm， Y方向偏移为-1.2mm～1.2mm。利用ANSYSworkbench11.0仿真计算每组数值，将计算结果导入Matlab软件中三维图型指令，得到相关三维网格图：

iy=1A，ix=0A，Fy与x0、y0之间的关系如图7；

iy=3A，ix=0A，Fy与x0、y0之间的关系如图8；

iy=5A，ix=0A，Fy与x0、y0之间的关系如图9。

图9　Y方向电流为5 A时，偏心距对承载力Fy的影响

由图7到图9可知，随着电流的增加，轴承承载能力增强。由图中偏心距对承载力影响可知，曲面的线性度较差，曲面不平整，随着X、Y方向偏心距的增加，出现了较为明显的非线性弯曲。说明混合磁悬浮轴承-转子系统存在着耦合。

2.3大气隙混合磁场以X、Y方向的偏移量为变量，混合磁悬浮轴承-转子系统力距耦合分析

和混合磁悬浮轴承-转子系统力耦合采用相同的方法，仿真分析，得到的数据图如下所示：

iy=1A，ix=0A，Ty与x0、y0之间的关系如图10；

iy=3A，ix=0A，Ty与x0、y0之间的关系如图11；

iy=5A，ix=0A，Ty与x0、y0之间的关系如图12。

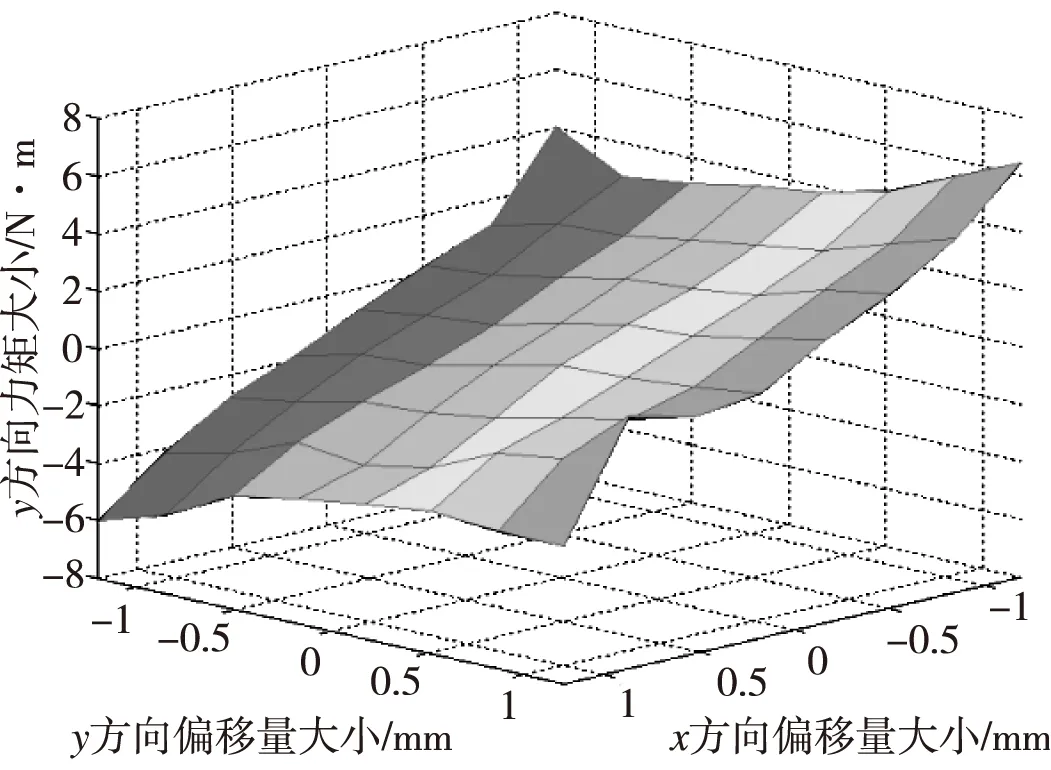
图12　Y方向电流为5 A时，偏心距对Ty的影响

由图10到图11可知混合磁悬浮轴承-转子系统存在着由耦合力引起的力矩耦合，该耦合力矩有正有负，且随着电流的增加，混合磁悬浮轴承-转子系统的耦合力矩变大。

2.4大气隙混合磁场以偏心距e为变量，混合磁悬浮轴承-转子系统沿转子圆周角度方向力耦合分析

现以偏心距e为变量，来讨论混合磁悬浮-转子系统电磁耦合特性，即当转子X、Y 方向电流为一定值时，研究e 对大气隙混合磁悬浮轴承承载力Fy的影响。

为确保Y方向磁力有一定大小同时消除X方向电流的影响，保证仅受单一要素影响，取ix=0，iy分别为1A、3A与5A，e分别取0.2mm～1.2mm。利用ANSYSworkbench11.0仿真计算每组数值，将计算结果导入Matlab软件中三维图型指令，得到相关三维网格图。

iy=1A，ix=0A，Fy与e、圆周角度θ之间的关系如图13；

iy=3A，ix=0A，Fy与e、圆周角度θ之间的关系如图14；

iy=5A，ix=0A，Fy与e、圆周角度θ之间的关系如图15。

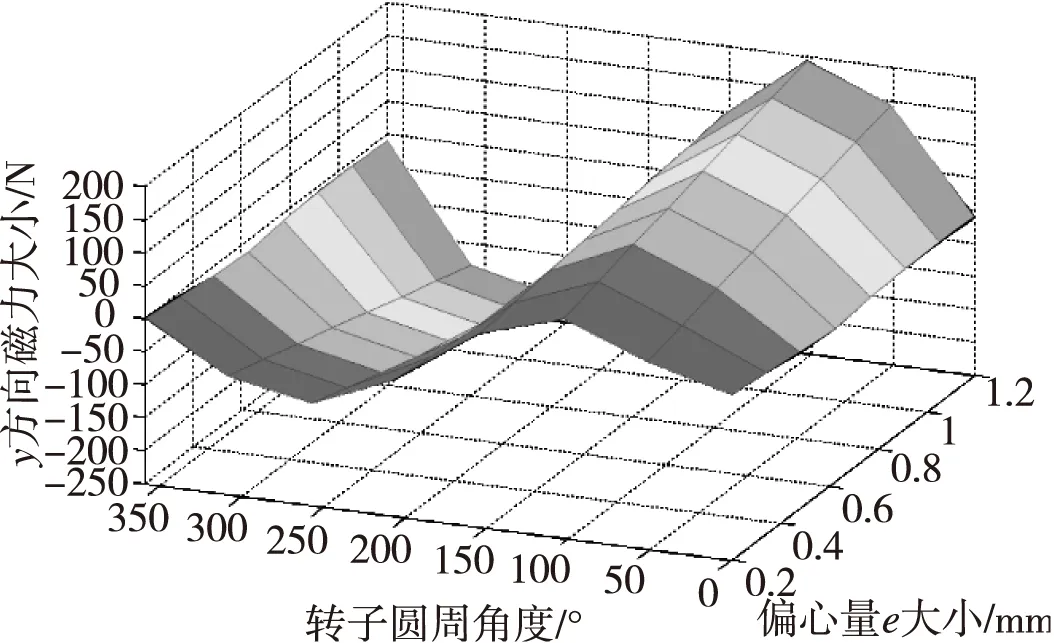
图15　Y方向电流为5 A时，偏心距e对承载力Fy的影响

由图13到15可知在相同偏心距e下，偏心的方位不同，承载不同；在同方位，不同的偏心距e，承载力也不相同。在同一偏心距e下，不同方位的承载力有正有负。由图中不同方位偏心距e对承载力影响图可知，曲面的线性度较差，曲面不平整，随着偏心距e的增加，出现了较为明显的非线性弯曲。说明混合磁悬浮轴承-转子系统存在着耦合。

2.5大气隙混合磁场以偏心距e为变量，混合磁悬浮轴承-转子系统沿转子圆周角度方向力矩耦合分析

图16　Y方向电流为1 A时，偏心距e对Ty的影响

和分析混合磁悬浮轴承-转子系统力耦合采用相同的方法，仿真分析，得到的数据图如下所示：

iy=1A，ix=0A，Ty与e、圆周角度θ之间的关系如图16；

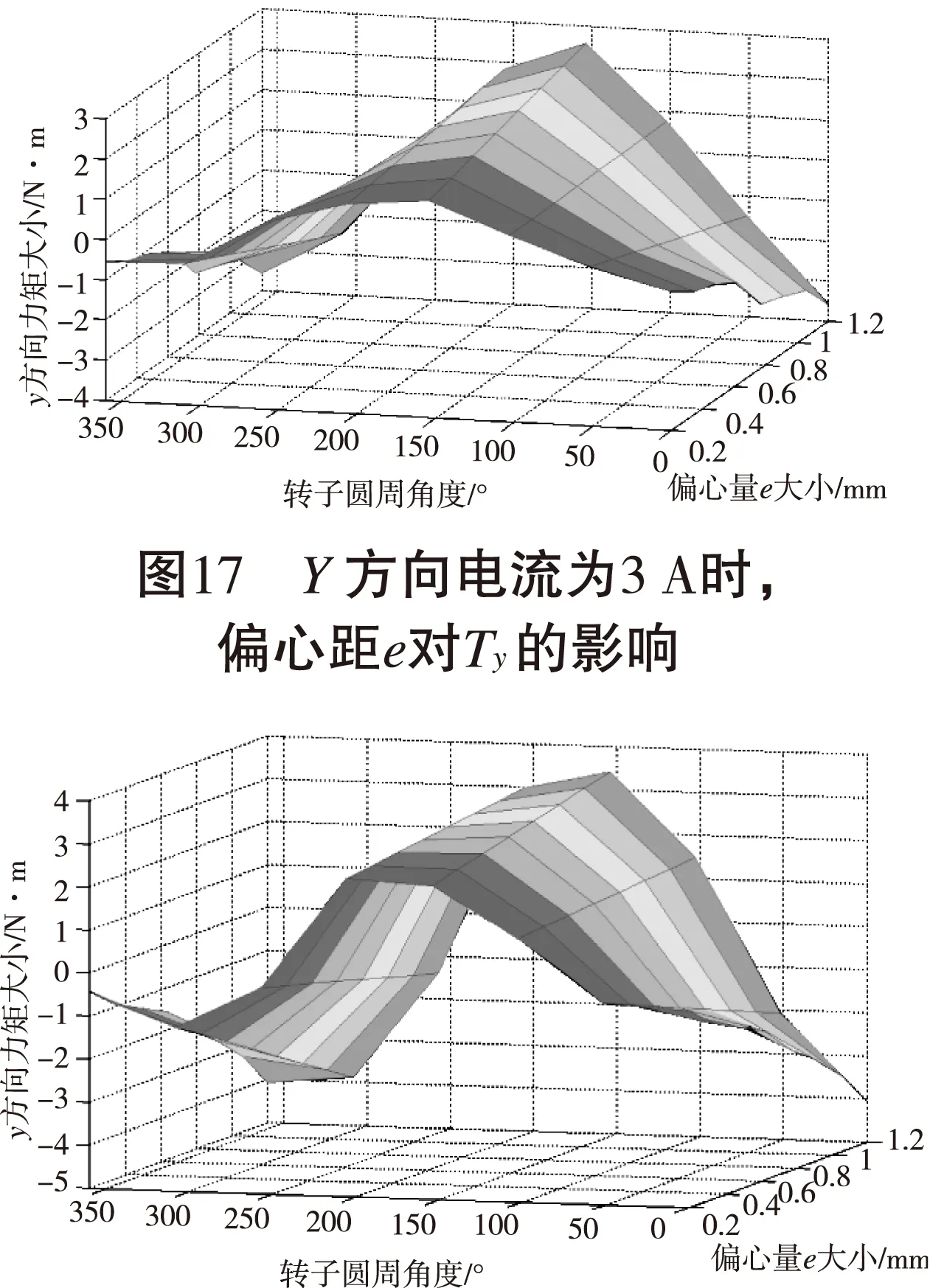
图18　Y方向电流为5 A时，偏心距e对Ty的影响

iy=3A，ix=0A，Ty与e、圆周角度θ之间的关系如图17；

iy=5A，ix=0A，Ty与e、圆周角度θ之间的关系如图18。

由图16到18可知混合磁悬浮轴承-转子系统存在着由耦合力引起的力矩耦合，该耦合力矩有正有负，且随着电流的增加，混合磁悬浮-转子系统的耦合力矩变大。在相同偏心距e下，不同偏心角θ对应的耦合力矩不同，有正有负，大小不一；在相同偏心角θ下，不同的偏心距e也对应不同的耦合力矩。

3结论

1)当转子处于平衡，只存在永磁偏置磁场时，进行永磁磁场磁场磁力线分布，磁感应强度仿真分析，发现漏磁较为严重，但耦合现象不明显。

2)利用ANSYS workbench 11.0 对大气隙混合磁悬浮轴承混合磁场以X、Y方向的偏移量为变量，发现混合磁悬浮轴承-转子系统存在力耦合与力矩耦合，且偏移量越大，耦合越明显。

3)利用ANSYS workbench 11.0 对大气隙混合磁悬浮轴承混合磁场以偏心距e、偏心角度θ为变量，发现混合磁悬浮轴承-转子系统存在力耦合与力矩耦合，且在相同偏心距e下，不同的偏心角θ对应的力与耦合力矩大小不一，有正有负；相同偏心角θ下，不同偏心距e对应大小不一的耦合力和耦合力矩。

参考文献

[1]胡业发,周祖德,江征风著.磁力轴承的基础理论与应用[M].机械工业出版社,2006.

[2]王晓光. 磁悬浮转子系统的耦合理论分析及实验研究[D].武汉理工大学,2005.

[3]王念先. 大气隙混合磁悬浮轴承相关理论及设计方法的研究[D].武汉理工大学,2013.

[4]高宇. 永磁偏置混合磁悬浮轴承的研究[J]. 机械设计与制造,2010(05)162-163.

[5]程昌利, 周瑾. 径向磁悬浮轴承磁场仿真及电磁力耦合分析[C]. 第五届中国磁悬浮轴承学术会议论文集, 2013.

[6]胡业发,周祖德,王晓光,吴华春. 磁力轴承转子系统的力耦合和力矩耦合分析[J]. 机械工程学报,2002,38(12):25-28.

[7]孙玉坤,朱熀秋,蔡兰. 三自由度混合磁悬浮轴承耦合特性[J]. 江苏大学学报(自然科学版),2006,27(04):342-346.

[8]王曦,房建成,樊亚洪,刘彬,李光军,刘刚. 磁悬浮飞轮用轴向力偏转永磁偏置轴向磁轴承磁路耦合特性[J]. 航空学报,2011,32(04):649-663.

[9]Han B C, Zheng S Q, Le Y, et al. Modeling and analysis of coupling performance between passive magnetic bearing and hybrid magnetic radial bearing for magnetically suspended flywheel[J]. IEEE Transactions on Magnetics, 2013,49(10): 5356-5370.

中图分类号：TH39

文献标识码：A

文章编号：1002-6886(2016)03-0010-05

作者简介：任茂发(1989-)，男，湖北荆州人，武汉理工大学机电工程学院硕士研究生，研究方向为磁悬浮技术。

收稿日期：2015-11-05

Simulation analysis of the coupling characteristics of large-air-gap hybrid magnetic levitation bearing-rotor system

REN Maofa, ZHENG Hao, LI Boyu

Abstract:Magnetic levitation is a method by which an object is suspended in certain position by controlled electromagnetic force, in no contact with its foundation. The working principle of the magnetic levitation bearing indicates that in working, there exists various coupling phenomena in its structure and control system. In this paper, we introduced the structure, characteristics and working principle of the large-air-gap hybrid magnetic levitation bearing, established its equivalent magnetic circuit model, and analyzed its magnetic field coupling characteristics using finite element method. With eccentricity as variable, we analyzed the force coupling and the torque coupling of the large-air-gap hybrid magnetic levitation bearing-rotor system. The results showed that, the larger the eccentricity was, the stronger the coupling would be.

Keywords:large air gap; hybrid magnetic levitation bearing; coupling characteristics; simulation