低维约当D-双代数的性质*

杜丽华，王　红

(辽宁师范大学 数学学院，辽宁 大连116029)



低维约当D-双代数的性质*

杜丽华，王红

(辽宁师范大学 数学学院，辽宁 大连116029)

摘要:主要研究低维约当D-双代数及其基本性质,它们是在约当代数的基础上得到的.首先找到上边界约当D-双代数的构造方法以及低维约当代数的分类,计算了这类约当代数上Yang-Baxter方程的张量形式的解.然后利用约当代数的配对可以得到每一类约当代数上对应的上边界约当D-双代数的代数运算,从而得到了低维上边界约当D-双代数的分类.

关键词:约当代数；约当D-双代数；约当Yang-Baxter方程

上世纪30年代,物理学家P.Jordan在研究量子力学时给出了约当代数的概念,从此约当代数走上了历史舞台.随着科技的发展,约当代数很快成为一个独立的代数体系并渗透到其他领域,除了在数学中有许多应用,在其他方面的应用也有很多,例如量子力学、量子群等等.本文主要讨论它的基本问题,例如约当D-双代数.本文利用约当Yang-Baxter方程,在经典Yang-Baxter方程的基础上,对于每一类约当代数找到约当Yang-Baxter方程的一个反对称解,在约当D-双代数结构的基础上,得到2、4、6维上边界约当D-双代数的分类.

1基础知识

定义1设J是域F上的线性空间,J中定义乘法运算:(x,y)→x•y,若满足下面的等式

x•y=y•x

(1)

((x•x)•y)•x=(x•x)•(y•x)

(2)

(∀x,y∈J)，则称J是域F上的一个约当代数.

定义2(J,•)是一个约当代数,V是域F上的线性空间,如果线性映射ρ:J→gl(V)满足下面的方程

[ρ(x),ρ(y•z)]+[ρ(y),ρ(z•x)]+

[ρ(z),ρ(x•y)]=0

ρ(x)ρ(y)ρ(z)+ρ(z)ρ(y)ρ(x)+ρ((x•z)•y)=

ρ(x)ρ(y•z)+ρ(y)ρ(z•x)+ρ(z)ρ(x•y)

其中，x,y,z,u∈J,[ρ(x),ρ(y)]=ρ(x)ρ(y)-ρ(y)ρ(x).则ρ是J的一个表示或一个模,记为(ρ,V)或ρ.

定义4设(J,•)是一个约当代数,如果线性映射Δ:J→J⊗J满足下面三个条件:

(1)Δ是对称的(或交换的),即Δ(x)=σ(Δ(x)),∀x∈J;

(2)Δ*:J*⊗J*→J*定义了线性空间J*上的一个约当代数结构;

(3)Δ满足,

Δ((x•y)•z)+(y⊗1)•((z⊗1)•Δ(x))+

(1⊗y)•((1⊗z)•Δ(x))+

(x⊗1)•((z⊗1)•Δ(y))+

(1⊗x)•((1⊗z)•Δ(y))+

(x⊗y+y⊗x)•Δ(z)=

(x⊗1)•Δ(y•z)+(y⊗1)•Δ(z•x)+

(z⊗1)•Δ(x•y)+(1⊗(y•z))•Δ(x)+

(1⊗(z•x))•Δ(y)+(1⊗(x•y)•Δ(z));

(3)

(Δ⊗id)((x⊗1)•Δ(y))+

(id⊗Δ)((1⊗x)•Δ(y))+

(σ⊗id)((id⊗Δ)((1⊗x)•(y)))+

(Δ⊗id)((1⊗y)•Δ(x))+

(id⊗Δ)((y⊗1)•Δ(x))+

(σ⊗id)((id⊗Δ)((y⊗1)•Δ(x)))=

(Δ⊗id)Δ(x•y)+

(1⊗x⊗1)•((id⊗Δ)Δ(y))+

(1⊗y⊗1)•((id⊗Δ)Δ(x))+

(x⊗1⊗1)•((id⊗σ)((Δ⊗id)Δ(y)))+

(y⊗1⊗1)•((id⊗σ)((Δ⊗id)Δ(x)))+

(1⊗Δ(x))•((id⊗σ)((Δ(y)⊗1)))+

(1⊗Δ(y))•((id⊗σ)((Δ(x)⊗1))).

(4)

则称该线性映射是一个约当D-双代数结构,记为(J,Δ)或(J,J*).

Δ(x)=(rg•(x)⊗id-id⊗rg•(x))r=

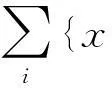
(5)

则约当D-双代数(J,Δ)称为上边界约当D-双代数.

定义6设(J,•)是一个约当代数,r∈J⊗J,方程(6)称为J上的约当Yang-Baxter方程,简记为JYBE.它也称为经典的Yang-Baxter方程在约当代数上的“约当代数类似”.

定理1设(J,•)是一个约当代数,r∈J⊗J.若r是反对称的,且[[r,r]]=0，其中,

[[r,r]]=r12•r13-r12•r23+r13•r23

(6)

则Δ:J→J⊗J可以诱导出J*上的一个约当D-双代数结构(J,Δ).

命题1设(J,•)是一个约当代数,r∈J⊗J是J上的约当Yang-Baxter方程的一个反对称解,则约当双代数D(J)上的约当代数结构“*”由如下关系给出.

a**b*=rg•*(r(a*))b*+rg•*(r(b*))a*,

∀a*,b*∈J*

(7)

x*a*=x•r(a*)-r(rg•*(x)a*)+rg•*(x)a*,

∀x∈J,a*∈J*

(8)

2低维约当D-双代数

(9)

同理可得:

(10)

设r是J上的约当Yang-Baxter方程的一个反对称解,则rij=-rji,于是

(11)

命题21维约当代数有两类R1,R2,其中,R1:e*e=e;R2:e*e=0.

3所得结果

定理22维上边界约当D-双代数的分类如下:

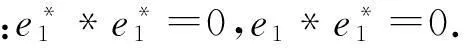
证明由(9)式和(10)式即可得出结论.

命题32维约当代数的分类如下:

定理34维上边界约当D-双代数的分类如下:

(1)对于B1:r矩阵为r=0.对应约当双D-代数中代数运算如下:

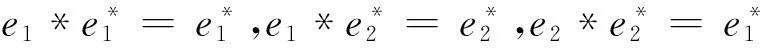
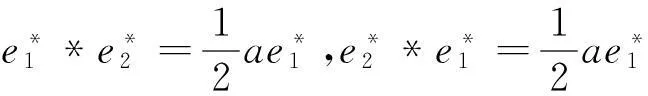
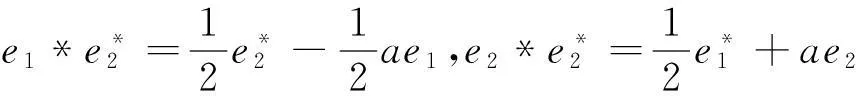
命题43维约当代数的分类如下,

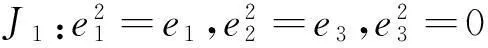
e1e2=e2,e1e3=e3,e2e3=0;

e1e2=e2,e1e3=e3,e2e3=0;

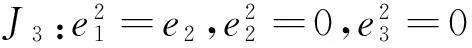
e1e2=e3,e1e3=0,e2e3=0;

e1e2=0,e1e3=e2,e2e3=0;

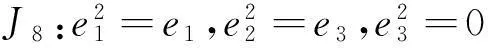
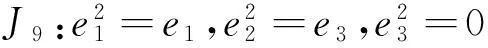
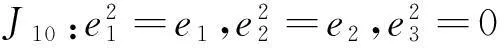
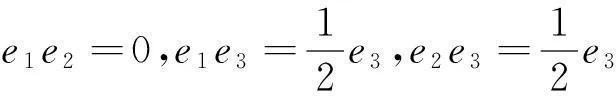
定理46维上边界约当D-双代数分类如下

(1)对于J1:r矩阵r=0,对应约当D-双代数中代数运算如下:

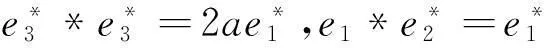
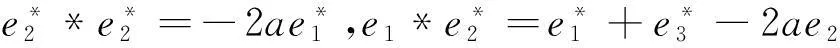
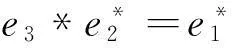
(5)对于J5:r矩阵r=0,对应约当D-双代数中代数运算如下:

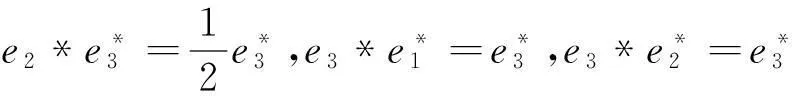
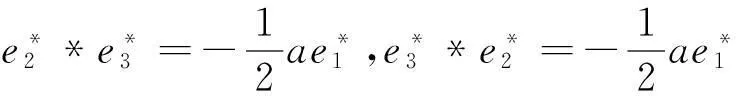
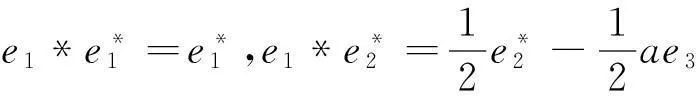
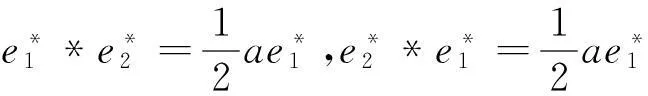
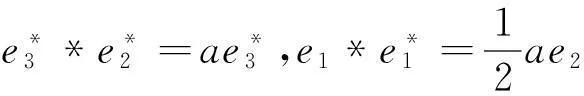
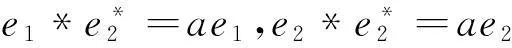
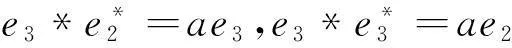
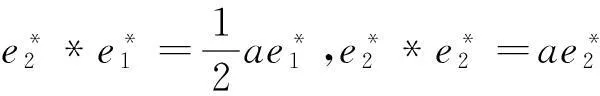
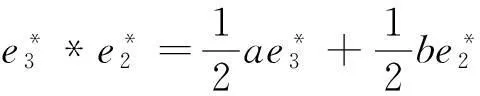
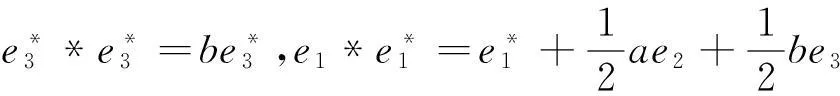
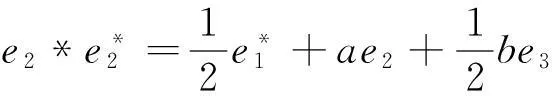
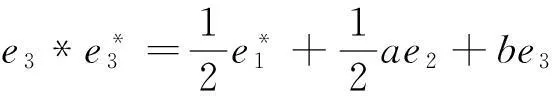
(8)对于J8:r矩阵r=0,对应约当D-双代数中代数运算如下:

(9)对于J9:r矩阵r=0对应约当D-双代数中代数运算如下:

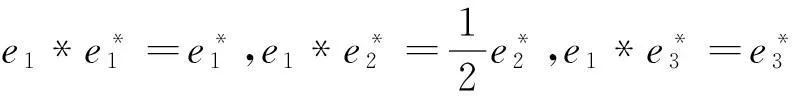
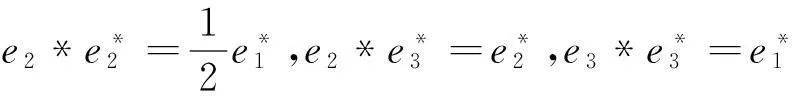
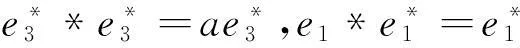
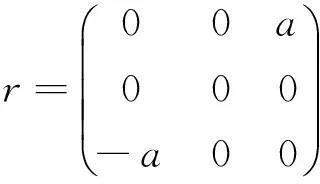
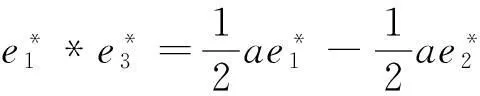
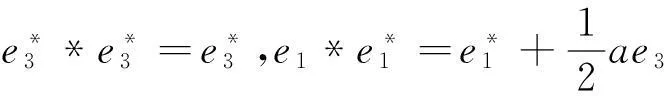
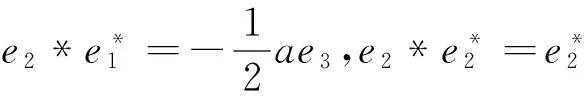
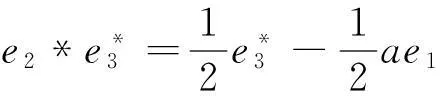
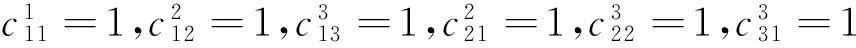
同理可算得其余9种情况.

参考文献：

[1]侯冬平.预约当代数和Loday代数的约当代数类似[D].天津:南开大学,2010.

[2]N Jacobson. Structure and representation of Jordan algebras[J].New York: Amer. Math. Soc. Colloq. Publ.,1968.

[3]V N Zhelyabin. Jordan D-bialgebras and symplectic form on Jordan algebras[J].Siberian Adv. Math, 2000,10(2): 142-150.

[4]N Jacobson. General representation theory of Jordan algebras[J]. Trans. Amer. Math. Soc.,1951,70: 509-530.

[5]Kashubal, M E Matin. Four dimensional Jordan algebras[J]. Int. J. Math. Game theory algebr,, 2012, 20(4):430-436.

[6]C M Bai. A unified algebraic approach to the classical Yang Baxter equation[J]. J. Phy. A: Math. Gen, 2007, 40(36): 11073-11082.

(责任编辑:陈衍峰)

DOI:10.13877/j.cnki.cn22-1284.2016.06.012

*收稿日期：2015-11-20

基金项目：辽宁省自然科学基金项目(20140428)

作者简介：杜丽华,山东济宁人,辽宁师范大学数学学院在读硕士．

中图分类号：O151.2

文献标志码：A

文章编号：1008-7974(2016)03-0032-04