基于排队论的航空通信频率干扰修复问题研究*

徐雪飞，李建华，杨迎辉，郭蓉

(1. 空军工程大学 信息与导航学院，陕西 西安　710077； 2. 中国人民解放军95983部队，甘肃 酒泉　732750)



指挥控制与通信

基于排队论的航空通信频率干扰修复问题研究*

徐雪飞1，李建华1，杨迎辉1，郭蓉2

(1. 空军工程大学 信息与导航学院，陕西 西安710077； 2. 中国人民解放军95983部队，甘肃 酒泉732750)

摘要：航空通信频率极易受到战场复杂电磁环境的影响。针对航空通信频率干扰普遍情形，提出了一种基于排队论的航空通信频率干扰修复资源调度方法。首先，分析了航空通信频率干扰问题，并从航空通信网络角度对频率干扰等级进行界定；然后，分析了实时、非实时频率资源调度模型，并以此为基础构建了混合频率资源调度模型，对其运算流程进行详细阐明；最后，对2种不同算例条件下混合频率资源调度模型的系统运行指标进行计算分析。结果表明：混合频率资源调度模型能够较好适应具有等级差异通信链路干扰修复情况，且不同频率资源调度子系统的数量配比对于混合频率资源调度模型的系统运行指标存在差异性影响。

关键词：航空通信频率；干扰修复；排队论；频率干扰等级；资源调度模型；运行指标

0引言

复杂电磁环境是现代战场的重要环境特征，是影响航空通信效果的重要因素。复杂电磁环境条件下的航空通信无时不刻不面临着各种各样的频率干扰问题。解决频率干扰问题一方面需要对干扰进行积极主动的对抗，另一方面则需要对干扰进行及时有效地修复。频率干扰修复问题可以划分为2个阶段性的问题。一是通过对频率干扰修复的环节和步骤进行分析，建立频率干扰修复模型；二是运用适当的评估手段和方法，对频率干扰修复的效果进行反馈式评价。本文主要针对前一个问题进行研究。

频率干扰修复问题本质上可以看作一个随机服务系统的排队服务问题[1]。修复频率干扰所造成的链路中断或损毁是服务对象，为其进行干扰修复服务的频谱管控系统则是服务系统，频谱管控系统修复干扰的能力和资源是有限的。因此，运用排队论方法可以较好地解决受约束条件下的频率干扰修复问题。现阶段，排队论在军事领域应用已经比较广泛。文献[2]基于排队论，构建了防空导弹服务概率模型，并对两种防空导弹武器系统进行作战效能的评估，并针对不同目标来袭密度，给出了各作战单元的作战效能。文献[3]运用排队论建立了舰艇编队协同防空排队模型，运用理论分析得到了整个编队毁伤目标概率为指标的防空效能，并通过对其进行计算仿真，分析了集中重要参数对防空效能的影响。类似相关军事应用领域运用排队论解决作战问题的文献还有很多，并且分别提出了针对性较强的排队论模型并进行了仿真计算[4-10]。但是，应用排队论在频谱管理领域进行资源的优化和调度还比较少见。为此，本文针对航空通信频率干扰修复资源调度问题，提出了一种基于排队论的频率干扰修复资源调度方法。通过对军事航空通信频率干扰问题进行分析，对频率干扰等级进行界定。在此基础上，结合实时、非实时频率资源调度模型，建立了混合频率资源调度模型。最后，通过对混合频率资源调度模型在不同算例条件下进行计算和分析，验证了模型的有效性。

1频率干扰问题分析

1.1频率干扰定义

定义1：军事航空通信频率干扰是指发生在航空通信过程中，针对航空通信网络以及通信链路所实施的各类能够导致有用信号接收质量下降、损害或阻碍等一切状态和事实的统称[11]。

根据对军事航空通信频率干扰的定义，本文对所研究军事航空通信频率干扰存在以下方面假定：

假定1：军事航空通信频率干扰主要发生在频率分配完成后、频率使用过程中。且此时的干扰是人为、积极主动式的干扰。即干扰的来源是敌对方主动的、有意识的通信对抗活动。因此，由于装备内部噪声和外部噪声造成的频率干扰不在本文研究范围内。

假定2：军事航空通信频率分配属于NP-完全问题，构成的航空通信网络具有复杂性和鲁棒性。因此，对航空通信网络进行毁灭性的全频段干扰只能在理想环境下实现。在实际作战环境中，全频段的干扰不仅难以发生，且需要付出极大的能量和资源代价。故假设对军事航空通信进行全频域毁灭性的干扰不存在，且此时对频率干扰进行修复也无意义。

假定3：军事航空通信依赖于无线信道进行信息传输，由于无线信道的开放性，故对其媒介特性的破坏和扰乱也会造成干扰，如核武器会造成电离层变化，从而导致短波通信完全失效。但对媒介特性的研究属于物理传播学领域的范畴。因此本文对由于媒介破坏造成的干扰修复问题也不做研究。

1.2频率干扰分析

军事航空通信频率干扰修复可以划归为排队论的研究范畴，但不同于传统排队论，军事航空通信频率干扰主要存在以下特殊问题：

(1) 是研究领域偏向信息域。军事航空通信频率干扰虽然和物理域存在密切联系，尤其是信道媒介的物理特性会对频率干扰造成严重影响。但军事航空通信频率干扰是承载于体系化和复杂化用户构成的通信网络结构之中，其干扰效果与通信网络的组织形式、承载业务的数量类型以及数据流转的方法方式都存在密切联系。故对军事航空通信频率干扰修复要从信息域角度进行考虑。

(2) 是研究内容网络性突出。军事航空通信频率干扰修复不仅是对通信链路干扰的修复，更是对通信网络干扰的整体修复。因此在对军事航空通信频率干扰进行修复过程中，一方面要从频率干扰修复的局部入手，从数据链路传输方面对频率干扰进行修复；更重要的是要从通信网络频率干扰的全局出发，从通信网络连通性角度对频率干扰进行全局的修复。

(3) 是研究角度等级性较强。军事航空通信频率干扰实质是对通信网络干扰。军事航空通信网络并不是简单的对等网络，其通信链路随着通信节点的重要性而存在等级区分，如由指挥节点构建的通信骨干网络比由功能任务节点构建的通信子网络通信级别要高，因此在受到频率干扰后，其修复的优先级也相对应较高。

1.3频率干扰等级界定

军事航空通信网络是由位于地面和空中各类固定和机动节点构成的网络结构，以节点之间的通信组织和指挥关系相互联结。根据文献[12-13]中关于军事作战复杂网络的描述和构建方法，将军事航空通信网络结构表示为一系列功能和类型不同的节点：指挥控制节点、火力打击节点、传感器节点、侦察监视节点等以及表示节点之间通信的连接边。军事航空通信频率承载于每一条通信链路之上，且军事航空通信频率干扰产生于信道传输过程中。军事航空通信网络结构如图1所示。

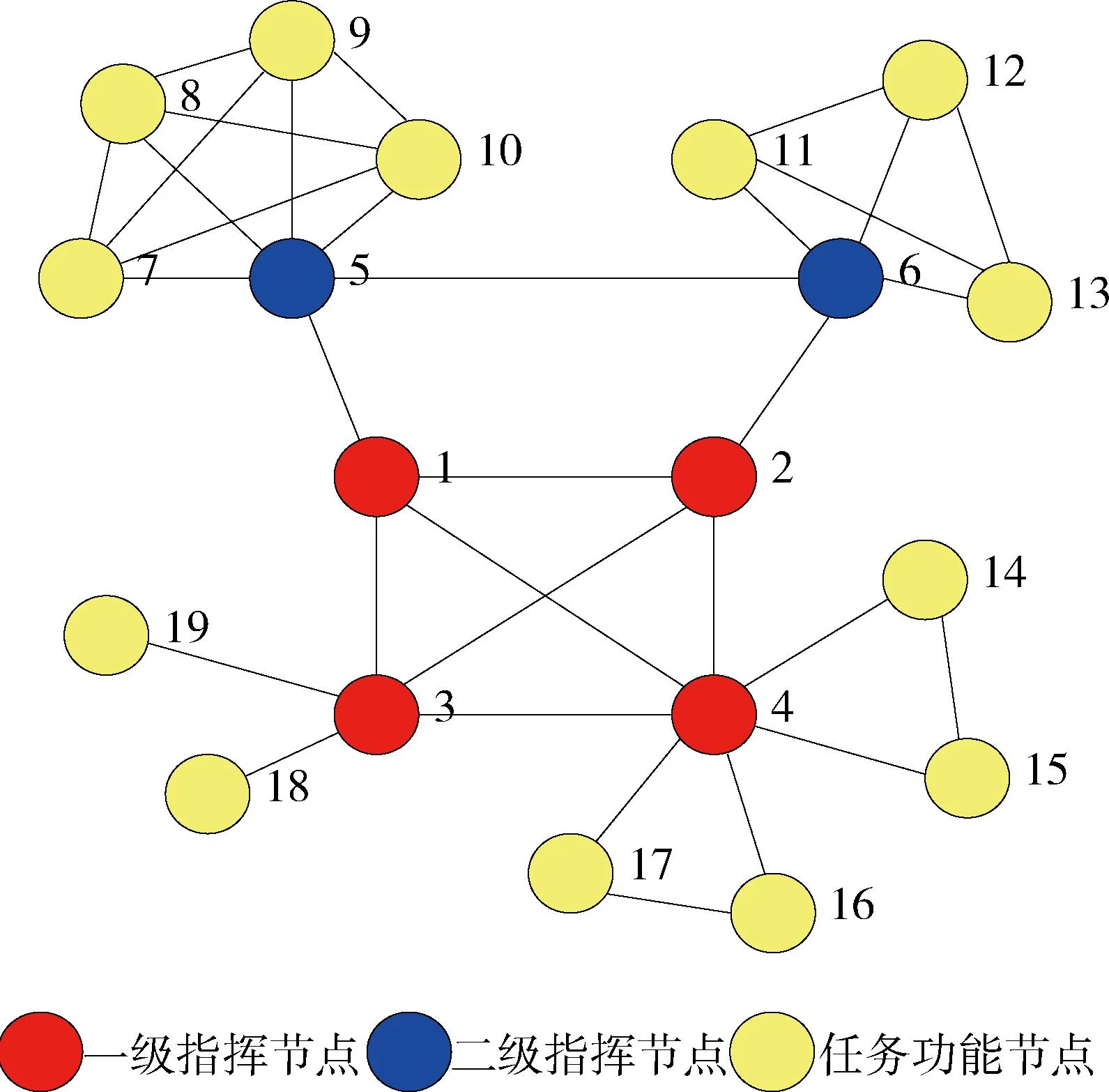
图1　军事航空通信网络Fig.1　Military aeronautical communication network

军事航空通信网络主要由3类节点构成。其中，一级指挥节点和二级指挥节点构成基本骨干网络，其他任务功能节点则以骨干节点为中心，构成社团结构的子网络。将军事航空通信网络用加权无向图的形式进行表现，可以表示为

G=(V,E)，

(1)

式中：V表示节点，即一级、二级指挥节点和任务功能节点；E表示连接节点的边，即节点之间互相通信分配的频率。由于军事航空通信频率分配网络图的邻接矩阵A可以表示为

A=(aij)N×N，

(2)

(3)

节点等级的差异势必会造成节点之间边的重要性差异，故将权值wij表示为以下三元组

(4)

式中：i,j=1,2,3，且分别表示一级指挥节点、二级指挥节点和任务功能节点。

2频率干扰修复资源调度分析

2.1排队论基本理论

排队论是研究系统随机聚散现象、随机服务系统工作过程的数学理论和方法[14-15]。其中，随机服务系统或排队系统是指对随机发生的事件提供一定服务的系统。其基本特征主要包括3类要素：①是输入过程。输入过程是指顾客到达服务系统所遵循的规律和时间分布情况，在军事航空通信频率干扰修复资源调度中特指需要被修复的链路；②是排队规则。排队规则是指顾客进入排队系统后，面对服务机构中其他需要被服务的顾客，所采取的排队的方法和方式。在军事航空通信频率干扰修复资源调度中具体指待修复链路的先后顺序；③是服务机构。服务机构是指为修复链路提供资源和信息帮助的组织和个体。在军事航空通信频率干扰修复资源调度中具体指频谱管控机构。根据上述描述，可以得出军事航空通信频率干扰修复资源调度排队系统模型如图2所示。

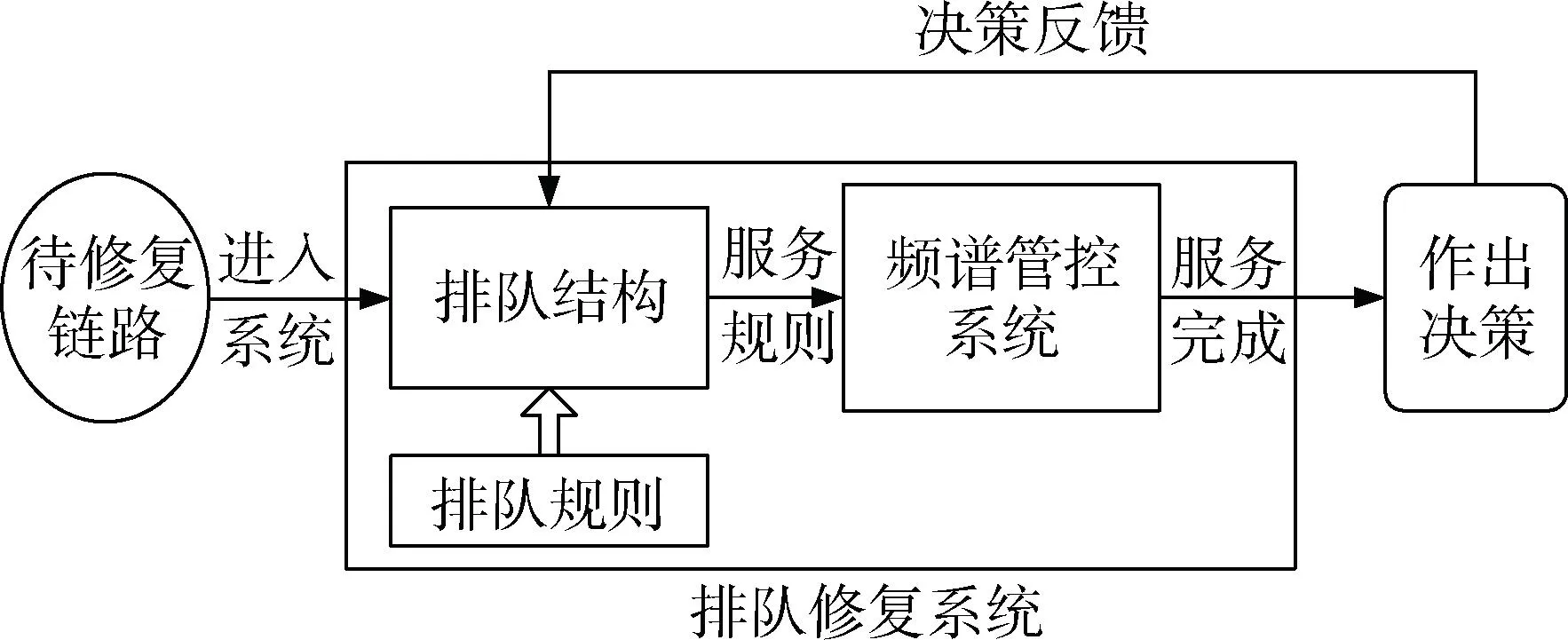
图2　频率干扰修复资源调度排队系统Fig.2　Frequency interference repairing resources schedule queuing system

2.2资源调度方法分析

军事航空通信频率干扰修复资源调度可以描述为以下过程：频率干扰发生于频率干扰网络中某一通信链路。首先，频谱管控系统将修复该链路作为一个事件录入排队修复系统。然后，排队修复系统根据该通信干扰链路的基本属性确定其重要等级，并作出修复决策。最后，排队修复系统结合频谱管控系统当前所处的状态为该事件调度合适的频谱管控资源进行修复。

在军事航空通信的场景环境中，频谱管控系统是由多个频谱管控子系统构成，每一个子系统都能够独立地同时对一个干扰链路进行修复。频率干扰网络中不同通信链路承担的任务不同，所以针对不同通信链路的修复存在优先级别和紧迫程度的差异。可以根据情况将资源调度的方式划分为3类：

(1) 实时频率资源调度方式

实时频率资源调度适合于对频率修复时间限制要求较高的通信链路。实时调度要求干扰修复在规定时间内开始并完成。如果干扰不能迅速得到修复和资源调度，则待修复通信链路重新向新的频谱管控子系统请求资源调度和修复工作。

(2) 非实时频率资源调度方式

非实时频率资源调度适合于对频率修复时间限制要求不敏感的通信链路。非实时调度对时间的要求并不严格，所以待修复的通信链路可以排队等待修复。但是，非实时调度还需要综合考虑修复通信链路所需资源和时间的均衡问题，使频谱管控子系统处于较均衡的修复工作负载状态。

(3) 混合频率资源调度方式

混合频率资源调度适合于对频率修复时间限制要求存在差异的通信链路。这些通信链路由于基本属性和功能的区别存在重要等级差异。骨干通信链路对修复的实时性要求高，非骨干类通信链路频率对修复实时性要求低。所以，修复这些通信链路可以综合运用实时与非实时资源调度方法，从而有效利用频谱管控系统的资源。

3频率干扰修复资源调度模型

将频谱管控系统和待修复的通信链路看做一个排队服务系统，通信链路受到随机的频率干扰导致断链，频谱管控系统根据通信链路的优先级别确定排队规则，待修复的通信链路按照制定好的排队规则进行修复。相关定义如下：

定义2：干扰输入分布

干扰输入是指在通信运用过程中，刻画敌方干扰我方正常通信而进行的通信频率干扰事件的到达规律。由于频率干扰发生的时间间隔具有一定的特征，通过对其进行特征分析，可以验证干扰输入分布服从的概率分布函数。

(1) 对于足够小的时间范围Δt内，在时间区间[t,t+Δt]内，频率干扰发生的概率Px与t无关，而与Δt成正比，可以表述为Px(t,t+Δt)=λΔt+o(Δt)，其中，o(Δt)表示当Δt趋近于0时关于Δt的高阶无穷小，λ为单位时间内频率干扰发生的概率。

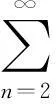
基于以上特征分析，可以将干扰输入过程描述为一个服从参数为λ的Poisson分布：

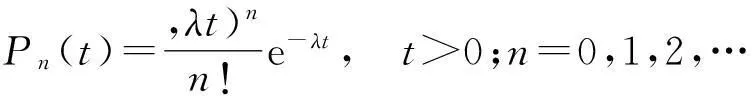
(5)

式中：n为频率干扰发生的次数。

定义3：干扰修复时间分布

干扰修复时间是指频率干扰被完全修复好的时间，即频率干扰从被修复的时刻起，到被修复完成时刻止的时间间隔。其通常也是一个随机变量。不同于干扰输入，干扰修复时间是时间段的概念。由于每个通信链路频率的干扰修复时间v是相互独立的随机变量，且服从相同的负指数分布。若假设对通信链路的干扰修复平均服务率为μ，即单位时间内被修复完成的通信链路的个数。进一步可得出干扰修复时间v的分布函数为

Fv(t)=P{v≤t}=1-e-μt,t≥0,

(6)

其分布密度为

fv(t)=μe-μt,

(7)

其数学期望为

E(v)=1/μ.

(8)

3.1实时频率资源调度模型

实时频率资源调度可以描述为以下过程：当通信链路发生频率干扰事件后，由于通信链路重要等级较高。所以频谱管控系统马上调度相关的频率资源进行干扰修复，此时不存在排队现象。具体可以运用M/M/n/0排队模型对该情况下的资源调度进行描述。

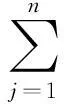
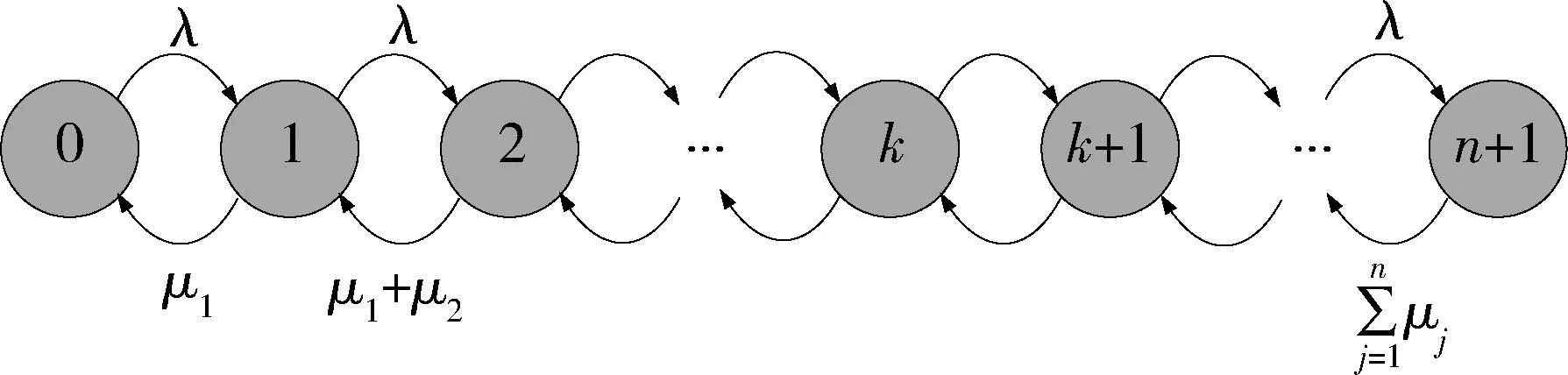
图3　实时频率资源调度状态转换图Fig.3　Real time frequency resources schedule state transition diagram

对实时频率资源调度进行分析，当频率干扰事件和干扰修复数量相等时，此时的实时频率资源调度处于一个稳定状态。此时可以建立平衡方程为

(9)

进一步可以得出实时资源调度运行指标分别为：

(1) 平均等待时间：Wq=0；

(2) 平均排队长度：Lq=0；

(3) 平均修复时间：Ws=1/μ；

(4) 平均队长：Ls=λ/μ(1-Pn+1)。

3.2非实时频率资源调度模型

非实时频率资源调度可以描述为以下过程：当通信链路发生频率干扰事件后，由于事件数量大于可以进行干扰修复的频谱管控子系统，即频谱管控子系统全部都处于工作状态。故没有接受频谱管控子系统进行干扰修复的事件处于一个排队等待的状态。进一步可利用M/M/n/m排队模型对该情况下的资源调度进行描述。

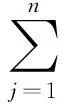
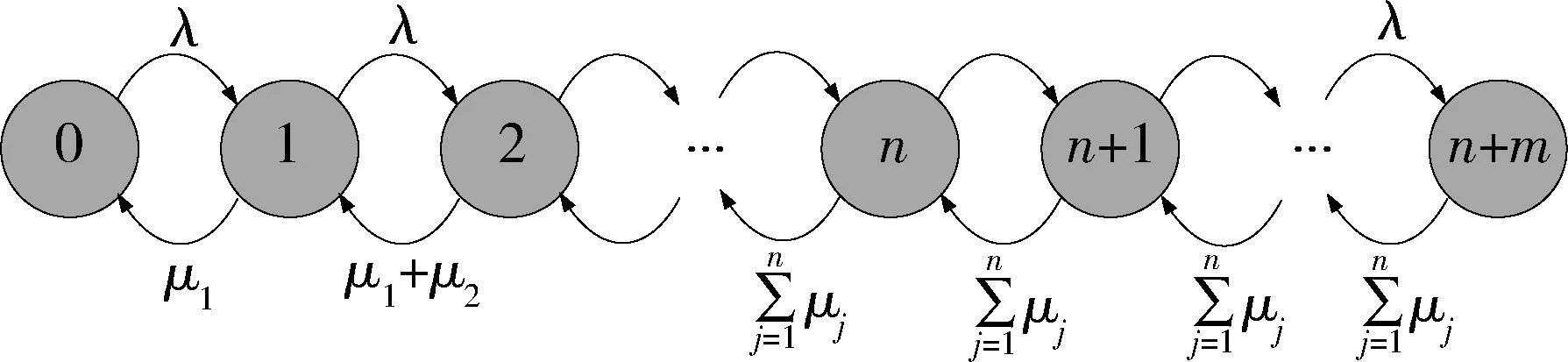
图4　非实时频率资源调度状态转换图Fig. 4　Non-real time frequency resources schedule state transition diagram

同样地，对非实时频率资源调度进行分析，当频率干扰事件和干扰修复数量相等时，此时的非实时频率资源调度处于一个稳定状态。此时可以建立平衡方程为

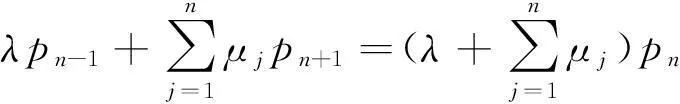
(10)

进一步可以得出非实时资源调度运行指标分别为

(1) 平均等待时间：Wq=Lq/λ；

(3) 平均修复时间：Ws=Wq+1/μ；

(4) 平均队长：Ls=Lq+λ/μ。

3.3混合频率资源调度模型

3.3.1模型构建

通常，实时资源调度和非实时资源调度是共同存在，且实时资源调度效率比非实时资源调度效率高。因此，混合资源调度能够更好地描述这种比较普遍的资源调度情况。混合资源调度可以描述为以下过程：当通信链路发生频率干扰事件后，各种不同的链路干扰事件相继到达，等待频谱管控系统的修复。此时，频谱管控系统遵循3条原则对通信链路进行修复：①优先级高的通信链路优先进行修复；②优先级相同的通信链路先到达先进行修复；③若全部频谱管控子系统都被占用，此时通信链路则按照优先等级排队等待修复。混合频率资源调度模型如图5所示。

运用概率的形式化方法对混合资源调度进行描述：若频率干扰事件i以参数为λ的一定分布规律到达，干扰事件以α的概率进入实时资源调度系统，以β的概率进入非实时资源调度系统，且α+β=1。且α和β可以分别表示为

(11)

(12)

由于实时资源调度系统和非实时资源调度系统之间可以相互转换，设ω1为实时修复的通信链路被调度至非实时资源调度系统的概率，ω2为非实时修复的通信链路被调度至实时资源调度系统的概率。故可得混合资源调度系统的状态方程为

(13)

3.3.2运算流程

混合资源调度模型的基本运行方式如下：

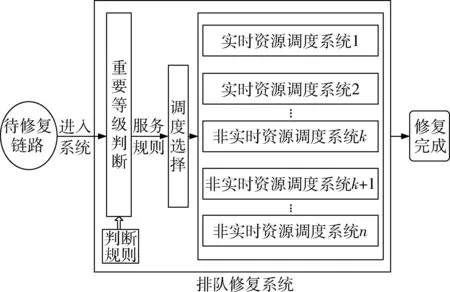
图5　混合频率资源调度模型Fig. 5　Hybrid frequency resources schedule model

Step 1：频率干扰事件以一定的分布规律进入排队修复系统。

Step 2：排队修复系统首先对待修复的通信链路进行重要度判断，如果通信链路的重要等级较高，则立即转入实时资源调度系统，全面调度有效资源对上述通信链路进行修复。

Step 3：如果通信链路的重要等级较低，则转入非实时资源调度系统，并根据情况调度有限的资源对上述通信链路进行修复。

Step 4：当实时资源调度系统全部处于工作状态，此时若有重要等级较高的频率干扰事件到达，则可以即时调用非实时资源调度系统进行修复。

Step 5：当非实时资源调度系统全部处于工作状态，实时资源调度系统处于空闲状态。此时若有重要等级较低的频率干扰事件到达，则在非实时资源调度系统中进行排队等待修复；若此时实时资源调度系统空闲，则可以向其发出资源调度请求，请求得到批准后方可利用实时资源调度系统进行修复。

Step 6：当所有实时和非实时资源系统都处于工作状态时，排队修复系统处于饱和状态，此时若有新的频率干扰事件进入，则根据该通信链路的重要等级进行选择性处理。如果其重要等级较高，则进入Step 4进行处理；如果其重要等级较低，则进入Step 5进行处理。

Step 7：当所有干扰修复完毕，排队修复系统进入修复值班状态。

4算例验证与分析

4.1同等级通信链路干扰修复

假设通信链路的重要等级相同，则该频率资源调度模型属于普通的M/M/n/m排队系统。若排队修复系统中资源调度子系统的数量为c，每个资源调度子系统的平均修复率为μ，则当排队修复系统的状态为n时，可得排队修复系统的平衡状态方程为

(14)

(15)

此时可以得出排队修复系统的运行指标分别为

(16)

4.2非同等级通信链路干扰修复

通信链路的重要等级可分为高、中、低3个等级，且高、中等级通信链路不仅可以利用实时资源调度系统进行干扰修复，在实时资源调度系统繁忙时也可以利用非实时资源调度系统进行干扰修复，而低等级通信链路只能利用非实时资源调度系统进行干扰修复。假设频率干扰事件的平均到达率为λ，且高、中、低3个等级通信链路发生干扰的概率相同。由于高、中等级通信链路修复是不允许排队等待，即一旦高、中等级通信链路出现干扰断链的情况，频率干扰修复资源调度系统需要立即发出响应，故此时可认为N=c，且此时的频率干扰修复资源调度系统是一个即时的排队系统，则可以得出此时排队修复系统的平衡状态方程为

(17)

进而可以得出排队修复系统的运行指标分别为

(18)

由于实时资源调度系统数量有限，当所有实时资源调度系统处于繁忙状态时，根据混合频率资源调度机制，干扰修复事件则转换到非实时资源调度系统进行修复，转换概率ω1为

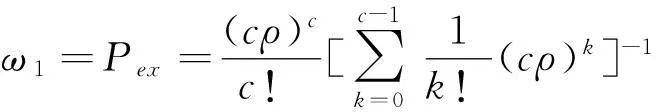
(19)

进而根据式(12)，(13)可得转换概率ω2为

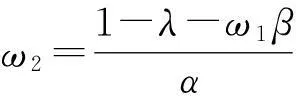
(20)

4.3结论计算与分析

通过对式(16)，(18)进行分析对比，显然，混合频率资源调度模型对于处理非同等级通信链路干扰修复具备优势，系统的运行指标Ls，Ws，Wq和Lq皆较小。下面对混合频率资源调度模型在不同数量资源调度子系统配置条件下的运行情况进行计算分析。假设干扰事件服从Poisson分布，平均到达率λ=1.0次/min，实时资源调度系统的个数为x个，非实时资源调度系统的个数为y个，且x,y≥1，x，y皆为整数。实时资源调度系统的平均修复率μx=0.5次/min，非实时资源调度系统的平均修复率μy=0.2次/min，则混合频率资源调度系统的平均修复率为μ=0.5x+0.2y/x+y次/min，ρ1/0.5x+0.2y≤1。

假设x+y=10，则根据上述约束条件可得x,y=(1,9)；x,y=(2,8)；x,y=(3,7)；x,y=(4,6)；x,y=(5,5)；x,y=(6,4)；x,y=(7,3)；x,y=(8,2)；x,y=(9,1)，分别计算出混合频率资源调度系统的运行指标如表1所示，绘制出系统运行指标变化趋势如图6所示。

从图6可以看出：总体上整混合频率资源调度模型的系统运行指标Ls，Ws随着实时资源调度系统

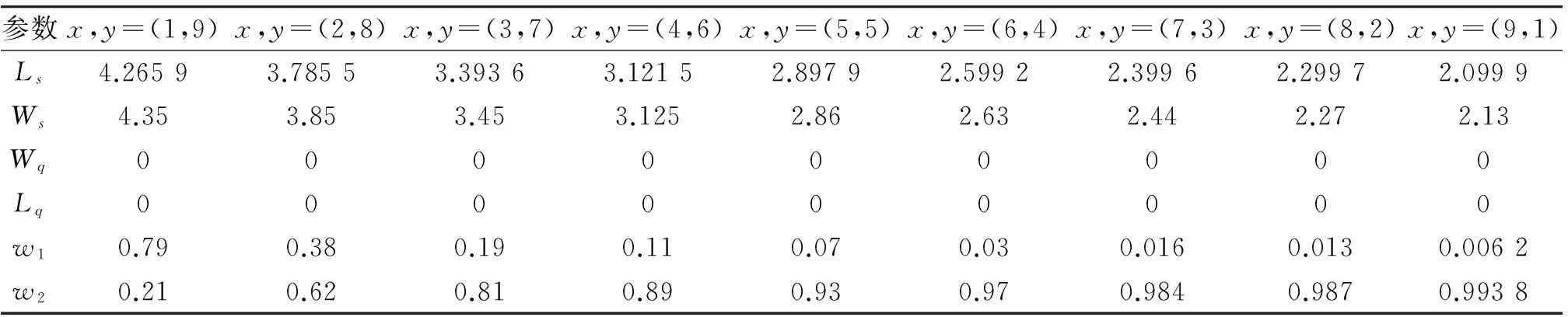
表1　不同配置条件下混合频率资源调度系统运行指标

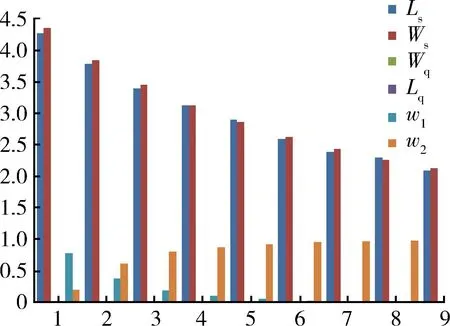
图6　混合频率资源调度系统运行指标变化趋势Fig. 6　Transformation direction of hybrid frequencyresources schedule system operation indexes

数量的增加、非实时资源调度系统数量的减小而逐渐降低。说明实时资源调度系统能够有效改善混合频率资源调度模型的系统运行指标，降低干扰事件在系统中的数量，并且能够降低每一个干扰事件在系统中的修复时间。同时，混合频率资源调度系统运行指标ω1随着实时资源调度系统数量的增加、非实时资源调度系统数量的减小而逐渐升高。意味着实时资源调度系统数量减少会导致干扰修复能力的下降，使得干扰事件从实时资源调度系统向非实时资源调度系统的转换概率增大。即混合频率资源调度模型的系统干扰修复能力下降。

对上述结论分析可得：混合频率资源调度模型系统的运行指标与资源调度子系统的数量配比密切相关。究其原因，是由于实时资源调度系统与非实时资源调度系统的干扰修复能力差异所导致。故从通信链路角度考虑，实时资源调度系统数量越多，每一个干扰事件的排队等待时间就越短，同时每一个干扰事件的修复效率也越高。但从混合频率资源调度系统的角度考虑，增加实时资源调度系统的数量意味着增加更多的运行成本开销，且当干扰事件的数量较少时，还会造成混合频率资源调度系统的闲置与浪费。所以要根据干扰事件的实际情况，结合混合频率资源调度系统的修复能力，合理规划配置实时与非实时资源调度系统的数量，使得混合频率资源调度系统能够有效完成干扰修复工作。

5结束语

本文对军事航空通信频率干扰问题进行分析，对航空通信频率干扰等级进行界定。基于排队论分析了实时、非实时频率资源调度模型，在此基础上构建了混合频率资源调度模型，给出了模型的运算流程和基本方法。在不同算例条件下对提出的模型进行计算分析，验证了模型的有效性和普适性，为军事航空通信频率干扰修复问题提供较好的理论支撑和技术指导。

参考文献：

[1]逯昭义. 通信业务量理论与应用[M]. 北京： 电子工业出版社, 2011.

LU Zhao-yi. Tele-Traffic Theory and Applications[M]. Beijing： Publishing House of Electronics Industry, 2011.

[2]赵广彤, 俞一鸣, 刘群，等. 基于排队论的防空导弹武器系统作战效能研究[J]. 现代防御技术, 2014, 42(1): 19-24.

ZHAO Guang-tong, YU Yi-ming, LIU Qun, et al. Research on Combat Effectiveness of Antiaircraft Missile Weapon System Based on Queuing Theory[J]. Modern Defence Technology, 2014, 42(1): 19-24.

[3]庞学亮, 程锦房. 基于排队论的协同防空作战效能分析[J]. 指挥控制与仿真, 2014, 36(3): 66-69.

PANG Xue-liang, CHENG Jin-fang. Combat Effectiveness Analysis of Cooperative Anti-Air of Warship Formation Based on Queuing Theory[J]. Command Control and Simulation, 2014, 36(3): 66-69.

[4]曹雷, 董强, 彭伟，等. 基于排队论的导弹防御系统的效能分析[J]. 南京理工大学学报, 2011, 35(4): 470-474.CAO Lei, DONG Qiang, PENG Wei, et al. Effectiveness Evaluation of Ballistic Missile Defense System Based on Queuing Theory[J]. Journal of Nanjing University of Science and Technology, 2011, 35(4):470-474.

[5]姜海波, 邱国新. 针对随机编队攻击的防空武器系统效能分析[J]. 舰船电子工程, 2014, 34(4):141-144.

JIANG Hai-bo, QIU Guo-xin. Effectiveness Evaluation of Air-Defense Weapon System Against Random Formation Attacking[J]. Ship Electronic Engineering, 2014, 34(4): 141-144.

[6]赵轶飞, 齐和平, 刘伶平，等. 排队论在军事信息服务中的应用[J]. 火力与指挥控制, 2011, 36(7): 111-118.

ZHAO Yi-fei, QI He-ping, LIU Ling-ping, et al. Application of Queuing Theory to Military Information Service[J]. Fire Control and Command Control, 2011, 36(7): 111-118.

[7]刘立佳, 李相民, 颜骥. 基于高维多目标多约束分组优化的要地防空扇形优化部署[J]. 系统工程与电子技术, 2013, 35(12): 2513-2520.

LIU Li-jia, LI Xiang-min, YAN ji. Key-point Air Defense Fan-Shaped Deployment With Large-Dimensional Multi-Objective Multi-Constraint Group Divided Optimization[J]. Systems Engineering and Electronics, 2013, 35(12): 2513-2520.

[8]喻春明, 迟玉红, 方艳东，等. 排队系统的非平衡动态指派模型及战时维修应用[J]. 东北大学学报, 2008, 29(11): 1617-1620.

YU Chun-ming, CHI Yu-hong, FANG Yan-dong, et al. Non-equilibrium Dynamic Assignment Model of Queuing System and Its Application in Wartime Equipment Maintenance[J]. Journal of Northeastern University, 2008, 29(11): 1617-1620.

[9]潘书山, 马大为, 李志刚. 混合类型防空体系作战效分析的排队网络方法[J]. 兵工学报, 2006, 27(5): 862-864.

PAN Shu-shan, MA Da-wei, LI Zhi-gang. Queuing Network Method for the Combat Effectiveness Analysis of Mixed-Mode Air-Defense Systems[J]. Acta Armamentarii, 2006, 27(5): 862-864.

[10]孟宪福, 张晓燕. 基于排队理论的对等网络任务调度模型[J]. 计算机集成制造系统, 2009, 15(11): 2140-2146.

MENG Xian-fu, ZHANG Xiao-yan. Peer to Peer Task Scheduling Model Based on Queue Theory[J]. Computer Integrated Manufacturing Systems, 2009, 15(11): 2140-2146.

[11]苟彦新, 王永民, 郭建新，等. 无线电抗干扰原理及应用[M]. 西安：西安电子科技大学出版社, 2005.

GOU Yan-xin, WANG Yong-min, GUO Jian-xin, et al. Radio Antijamming Communications Fundaments and Applications[M].Xi′an: Xidian University Press, 2005.

[12]金伟新, 肖田元. 作战体系复杂网络研究[J]. 复杂系统与复杂性科学, 2009, 6(4): 12-25.

JIN Wei-xin, XIAO Tian-yuan. Research on the Combat SoS Complex Network[J]. Complex Systems and Complexity Science, 2009, 6(4): 12-25.

[13]张勇, 杨宏伟, 白勇. 基于复杂网络的武器装备重要度评估方法[J]. 装甲兵工程学院学报, 2012, 26(1): 5-9.

ZHANG Yong, YANG Hong-wei, BAI Yong. Evaluation Method for Weapons Important Degree Based on Complex Networks[J]. Journal of Academy of Armored Force Engineering, 2012, 26(1): 5-9.

[14]陈永光, 柯宏发. 电子装备试验与训练最优化技术和方法[M]. 北京: 国防工业出版社, 2010.

CHEN Yong-guang, KE Hong-fa. Optimization Technology and Method for Electronic Equipment Test and Training[M]. Beijing: National Defense Industry Press, 2010.

[15]曹迎槐, 尹健. 军事运筹学[M]. 北京: 国防工业出版社, 2013.

CAO Ying-huai, YIN Jian. Military Operations Research[M]. Beijing: National Defense Industry Press, 2013.

Repair of Aeronautical Communication Frequency Interference Based on Queuing Theory

XU Xue-fei1, LI Jian-hua1, YANG Ying-hui1, GUO Rong2

(1.AFEU，Information and Navigation College,Shaanxi Xi’an 710077, China;2. PLA,No. 95983 Troop,Gansu Jiuquan 732750, China)

Abstract:Aeronautical communications frequency is vulnerable to interference under the war-field complex electromagnetic environment. Aiming at the common condition of aeronautical communication frequency interference, a method of resource scheduling of aeronautical communication frequency interference repairing based on queuing theory is proposed. Firstly, the frequency interference problem is analyzed, and the levels of frequency interference from the perspective of aeronautical communication network are defined; secondly, the real-time frequency resources schedule model and non-real time frequency resources schedule model respectively, and a hybrid frequency resources schedule model is structured on this basis, then the calculate processes of it is given in details; Finally, calculated and analyzed the system operation indexes under two different examples. The result showed that: the hybrid frequency resources schedule model could adapt the difference-levels communication link interference repairing better, and different number proportion of frequency resources schedule sub-systems could reach the difference effects for operation indexes of it.

Key words:aeronautical communications frequency; interference repairing; queuing theory; levels of frequency interference; resources schedule model; operation index

*收稿日期：2015-06-12；修回日期：2015-09-01

基金项目：国家社科基金资助项目(12GJ003-130)

作者简介：徐雪飞(1986-)，男，陕西西安人。博士生，主要研究方向为频谱管理控制与规划运用。

通信地址：710077西安丰镐路1号空军工程大学信息与导航学院E-mail：xxf19861128@sina.com

doi:10.3969/j.issn.1009-086x.2016.03.010

中图分类号：TP399

文献标志码：A

文章编号：1009-086X(2016)-03-0057-09