非线性分类结合平面变换的雷达信号分选方法*

刘志鹏，张国毅，田润澜

(空军航空大学，吉林 长春　130022)



探测跟踪技术

非线性分类结合平面变换的雷达信号分选方法*

刘志鹏，张国毅，田润澜

(空军航空大学，吉林 长春130022)

摘要：现有的对已知雷达分选方法存在识别速度慢、效率低，脉冲丢失敏感以及脉冲序列提取不完整等问题，为此提出了一种非线性分类器结合平面变换的雷达信号分选方法。该方法首先提取载频、脉宽、脉內调制等单脉冲分类特征，利用非线性分类器实现单脉冲识别，然后根据识别结果调取对应参数，通过平面变换完成对脉冲串的抽取。仿真实验表明，该方法具有速度快，准确率高，易于实现等优点。

关键词：雷达；分选；非线性分类器；平面变换；矢量神经网络；识别率

0引言

现代电磁环境日趋复杂，脉冲数量急剧增多，未来可能达到120万脉冲/s的量级[1]。如此高脉冲密度的环境对算法的准确性和实时性提出严峻考验；另一方面，如果能充分利用数据库中的雷达数据，对环境中的已知雷达脉冲进行预先分选，将极大提高分选的速度和准确度，同时降低脉冲流密度，进而大大减小对未知辐射源信号的分选难度[2]。

目前对已知雷达信号分选的方法主要有：PRI关联法、多参数匹配法，脉冲样本图法。PRI关联法需多次选择PRI进行试探性匹配，分选效率低，对脉冲干扰和脉冲丢失敏感[3]。多参数匹配法利用已装订的RF,PW等参数的上下限，将介于其间的脉冲分选出来[4-5]。该方法仅限于脉冲参数固定且不同雷达参数域不交叠的情况，不适用现代复杂高密度的脉冲环境。脉冲样本图法[6]综合了多参数匹配法和PRI关联法，虽然减少了试探性匹配的盲目性，但判别阈值及加权距离需人为先验设定，同时该方法对脉冲丢失敏感。

针对上述问题，本文提出一种非线性分类结合平面变换(nonlinearclassifiersandplanetransformation，NCPT)方法，可以适用于复杂体制雷达信号的分选，且具有速度快，准确率高，对干扰和脉冲丢失不敏感及易于实现等优点。

1NCPT方法

NCPT方法由2部分算法串联构成。第1部分为非线性分类器算法；第2部分为平面变换脉冲串抽取算法。算法示意如图1所示。

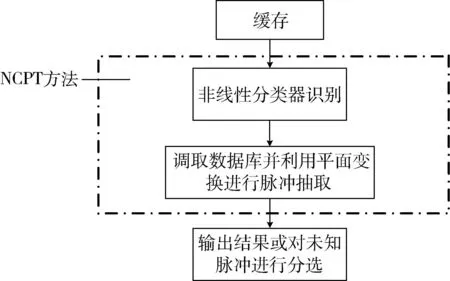
图1　NCPT方法示意Fig.1　NCPT method

首先将一定数量的脉冲序列放入缓存，读取某一未标记脉冲，经非线性分类器初识别后，记录识别结果，并标记此脉冲；根据识别结果调取数据库对应雷达的平面变换参数，并利用该参数对缓存内剩余脉冲进行平面变换并抽取；直到缓存内脉冲全部被抽取或被标记，输出分选结果或对剩余脉冲进行处理，同时更新缓存，继续按以上步骤进行处理。

1.1非线性分类器的选择及改进

由于现代复杂体制雷达信号在参数域上交叠，具有不连续，线性不可分的特点，故本文选用非线性分类器对其进行识别。人工神经网络是典型的非线性分类器，具有成熟的理论基础及良好的现实表现，其可以自适应数据，逼近任意函数及较强的容错能力使其始终为模式识别中讨论的焦点[7-8]。常见的神经网络分类器有BP神经网络，径向基函数神经网络及概率神经网络，这些分类器虽然在处理标量类型的数据时取得了良好的效果，但无法对参数捷变这种区间类型的数据进行有效识别[9]。对此，文献[10]提出一种矢量神经网络(vectorneuralnetwork,VNN)，兼备有处理区间类型和标量类型数据的能力。

1.1.1矢量神经网络

VNN的网络结构为n-l-m，即有n个输入节点，l个隐层节点，m个输出节点，如图2所示，实线箭头表示正向传播，虚线箭头表示反向传播，其激活函数f为sigmoid函数。

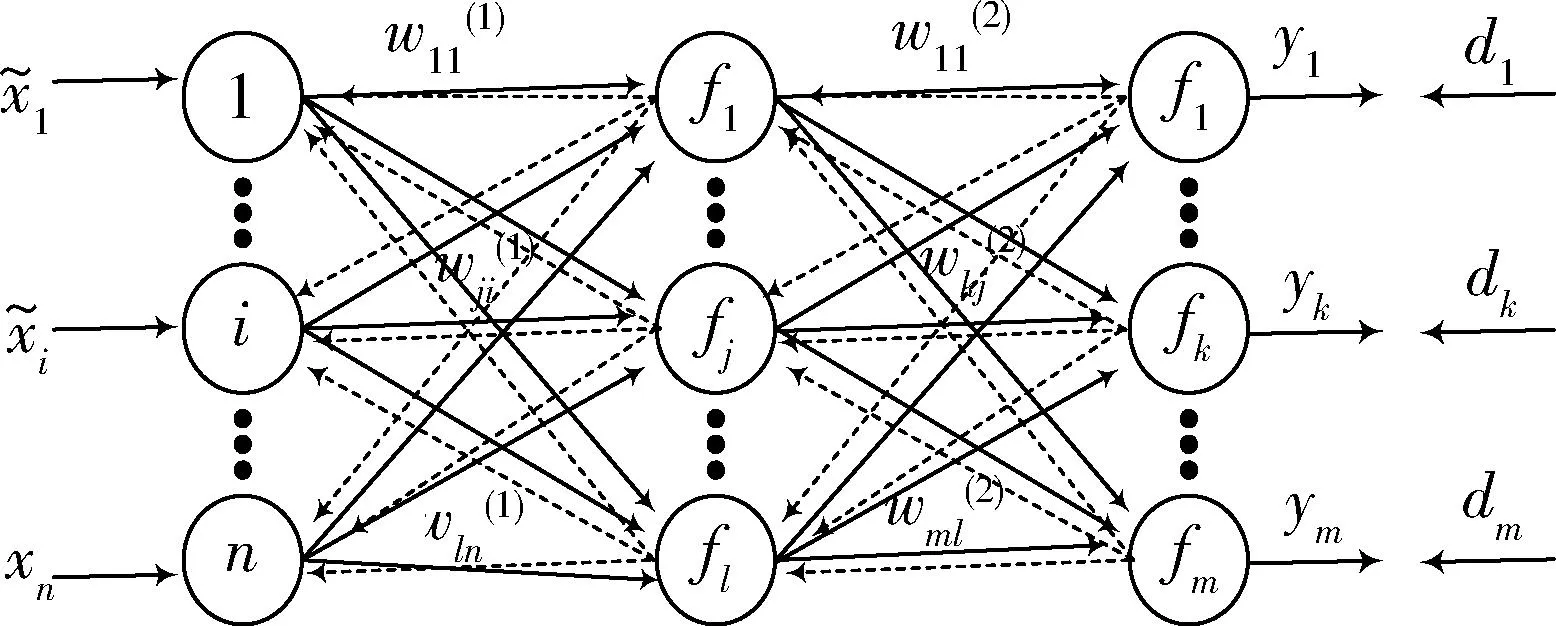
图2　VNN结构示意Fig.2　Structure of VNN

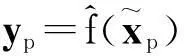
(1)

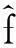
其误差计算方法为NVTBP[8]：

(2)

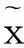
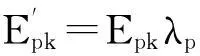
(3)

进而VNN的总误差为

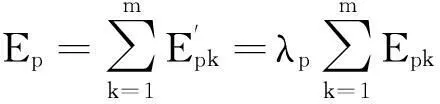
(4)

样本可靠性系数λp的引入进一步提高了矢量神经网络的识别准确率，然而文献[11]求解系数λp的方法为主观人为设定，缺乏计算依据。本文提出一种利用熵权值确定样本可靠性的方法，该方法使得求解系数λp具有了实际可操作性，实验证明，该方法可大大提高VNN网络的识别率和容错能力。

1.1.2基于熵权的样本可信度计算

信息熵反映了系统提供信息量的大小，信息熵值越大，则系统提供信息量越小，信息就越不可靠，因此，考虑利用样本的信息熵所确定的权值来表征其可信度。

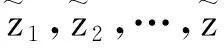
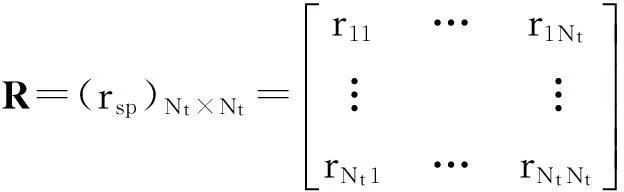
(5)

对参数Ci的第s个区间，其信息熵：

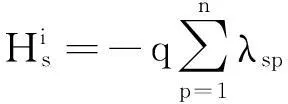
(6)

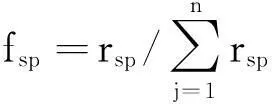
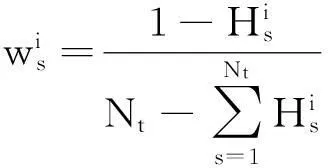
(7)

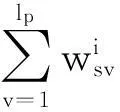
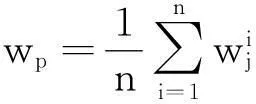
(8)

将wp归一化后即可作为VNN网络的样本可靠性系数，改进后的后向传播方法称为熵权值矢量后向传播算法(entropyweightvector-typebackpropagation，EWVTBP)。

1.2PRI平面变换

文献[13]提出了对PRI周期调制信号的平面变换方法，当PRI未知时，该方法可操作性不强。本文通过引入平面变换因子，充分发挥出该方法的搜索速度快，对脉冲丢失不敏感等优点。

1.2.1平面变换原理

假设第i个脉冲的到达时间为TOAi，按式(9)计算：

(9)

式中：⎣x」表示向下取整，mod(x,y)表示取余函数，W为平面变换窗长度，N为脉冲个数。文献[14]证明，当信号PRI与平面变换窗W满足一定关系时，若将(xi,yi)以坐标形式表示到平面上，则PRI周期调制信号的点迹会在二维平面形成规律曲线；反之，若信号PRI与变换窗长度不满足相应关系，则变换的点迹在平面上呈无规律散乱的分布。由此启发，通过选择窗宽，利用平面变换得到的点迹曲线就可以完成对脉冲的提取。

1.2.2平面变换抽取算法

假设某已知雷达信号在工作模式i时，其PRI有N种调制类型，定义平面变换因子(planetransformationfactor，PTF)：

PTF=(W,P,T),

(10)

式中：W=(w1,w2,…，wN)为平面变换窗宽向量；P=(p1,p2,…，pN)为曲线搜索模式向量；T=(t1,t2,…,tN)为搜索容差向量。

于是对于交叠的脉冲串，一旦得到其中某部雷达的PTF，就可以根据窗宽W做平面变换，得到规律点迹曲线，再由搜索模式P和搜索容差T将曲线上点对应脉冲全部快速抽取出来。

PTF由其对应的PRI值和类型确定，对于PRI调制类型为固定、参差的信号，选择窗宽使W与PRI值相等(PRI固定信号)或W与PRI骨架周期相等(PRI参差信号)，此时平面变换点迹为垂直于x轴的直线，故搜索模式P为寻找所有与x轴垂直曲线上的点，搜索容差T由雷达发射机本振及侦察接收机测量误差决定，一般取值较小，其他几种常见PRI调制类型的PTF确定规则总结见表1。

1.3NCPT技术流程

NCPT技术流程总结如下：

(1) 对侦察到的辐射源信号进行特征提取，将提取特征后的脉冲送入缓存，直到缓存中脉冲个数到达一定数量或脉冲累积时间达到门限。

(2) 读取缓存中首个未处理脉冲并标记，利用VNN采用EWVTBP算法进行识别并根据识别结果调取数据库中对应雷达的PTF。

(3) 利用PTF中的窗宽对缓存中未标记脉冲进行平面变换，再根据PTF中的搜索模式和容差参数进行脉冲抽取；若PTF存在多值情况，则对PTF依次取值。

(4) 重复步骤(2)、(3)，直到缓存内所有脉冲均被抽取或被标记，输出结果或进行后续处理。

(5) 清空缓存，开始步骤(1)。

2雷达信号分选实验

设计3组仿真实验，分别测试VNN识别部分的效果，平面变换抽取算法的有效性以及NCPT方法的有效性。仿真环境：Windows7,AMDCPUA6, 4GB内存，编程工具为Matlab7.10.1。

2.1VNN识别测试

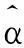
在测试阶段， 构造160个测试样本，4部雷达中每部对应40个测试样本，测试样本随机在训练样本中对应雷达参数区间中取值。为验证VNN对测试样本测量误差的容错能力，定义误差偏离范围EDL(errordeviationlevel)[10]：

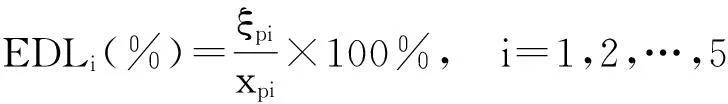
(11)

式中：xpi表示第p个测试样本第i个参数值，ξpi为随机添加到xpi的误差偏离值。将测试样本的EDL从0开始逐渐增加到16%，分别利用NVTBP算法和EWVTBP算法进行测试， 结果见图3。实验表明，

表1　PTF确定规则

一旦VNN训练完成，即可实时的给出测试样本对应类别， 在测试样本参数没有偏差的情况下，EWVTBP算法的识别正确率可达98.8%，而NVTBP算法只有93.2%。当EDL为0时，EWVTBP算法的识别率比NVTBP算法高6%，随着EDL的增加，NVTBP算法性能下降明显，而EWVTBP算法表现出了更好的对测量偏差的容错性能。

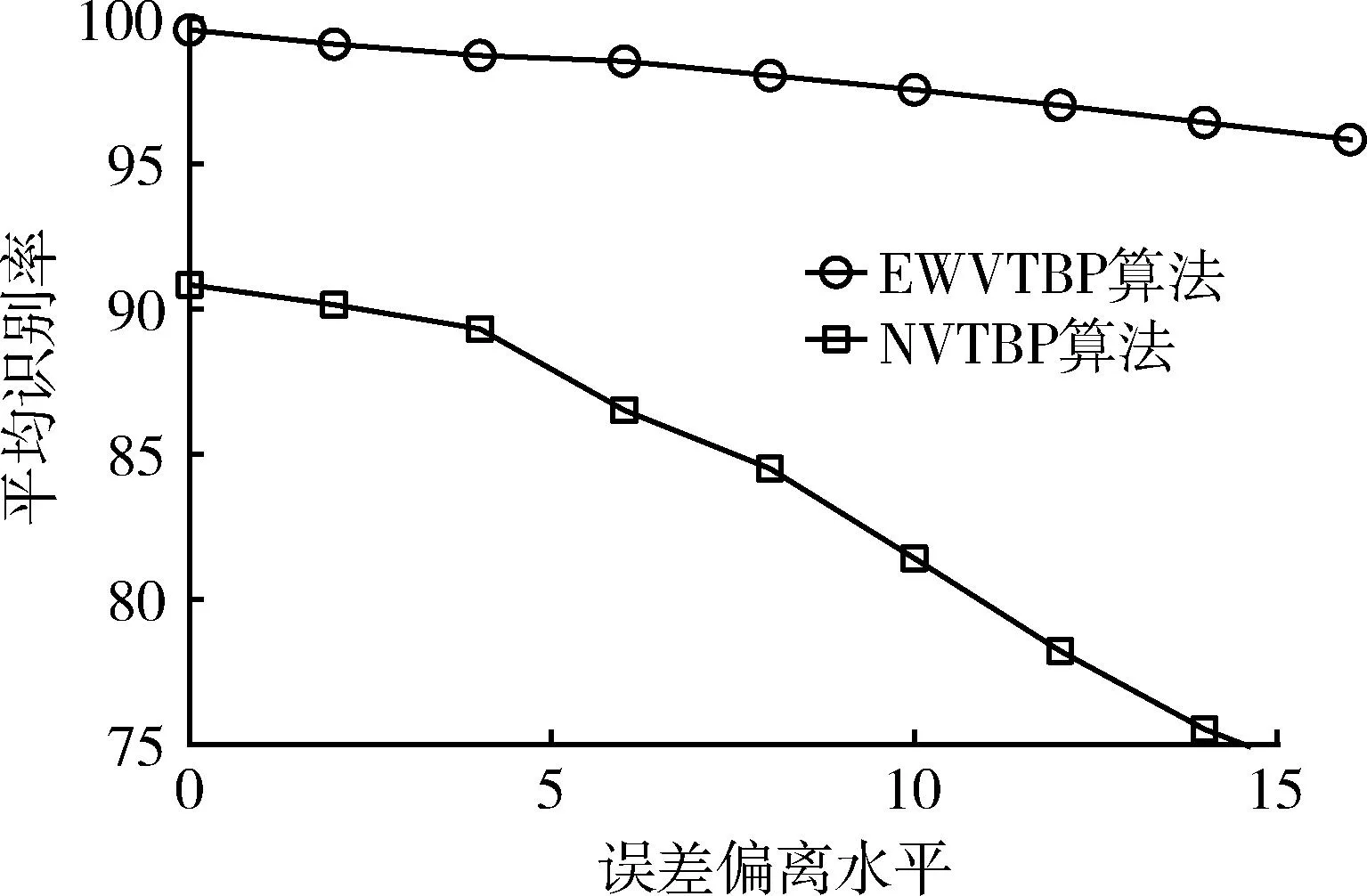
图3　EWVTBP算法识别效果Fig.3　Performance of EWVTBP

2.2平面变换抽取技术实验

定义脉冲分选准确率和脉冲抽取率分别为

(1) 脉冲分选准确率

RC=(SC/S)×100%，

(12)

式中：S是分选出同一部雷达的脉冲数，SC是分选正确的脉冲数；

(2) 脉冲抽取率

RE=(SC/SR)×100%，

(13)

式中：SR是所分选雷达实际脉冲数，SC同上。

易见，RC越高，分选效果越好，分选结果的可信度越高；而对于已知信号的分选，还要求有较高的RE指标，这是为了减小脉冲密度，保证下一步对未知雷达信号的分选有较高的准确率和处理速度。

为检验平面变换算法的效果及PTF选取的合理性，对不同类型雷达进行仿真实验，实验数据参数和PTF取值见表3。实验中将脉冲串按到达时间进行混叠，分别考虑脉冲丢失和混入干扰脉冲的影响，实验结果如图4所示。从图4a)可知，脉冲丢失对平面变换抽取算法效果影响不大，在脉冲丢失率为40%的时候，总的脉冲分选准确率RC及脉冲抽取率RE仍大于99%；从图4b)可知，随着干扰脉冲的增多，平面变换抽取算法效果略有下降，这是由于平面点密度增高所造成的，然而即使混入干扰脉冲达到已知雷达脉冲数目的200%时，RC和RE值仍高于94%，证明平面变换抽取算法几乎可以彻底的抽取已分选雷达脉冲。

2.3NCPT方法实验

利用某次侦察的一段实测数据对NCPT技术进行测试，经人工分析，测试数据中共包含11部不同雷达的脉冲数据，选择其中7部雷达编入数据库。

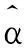
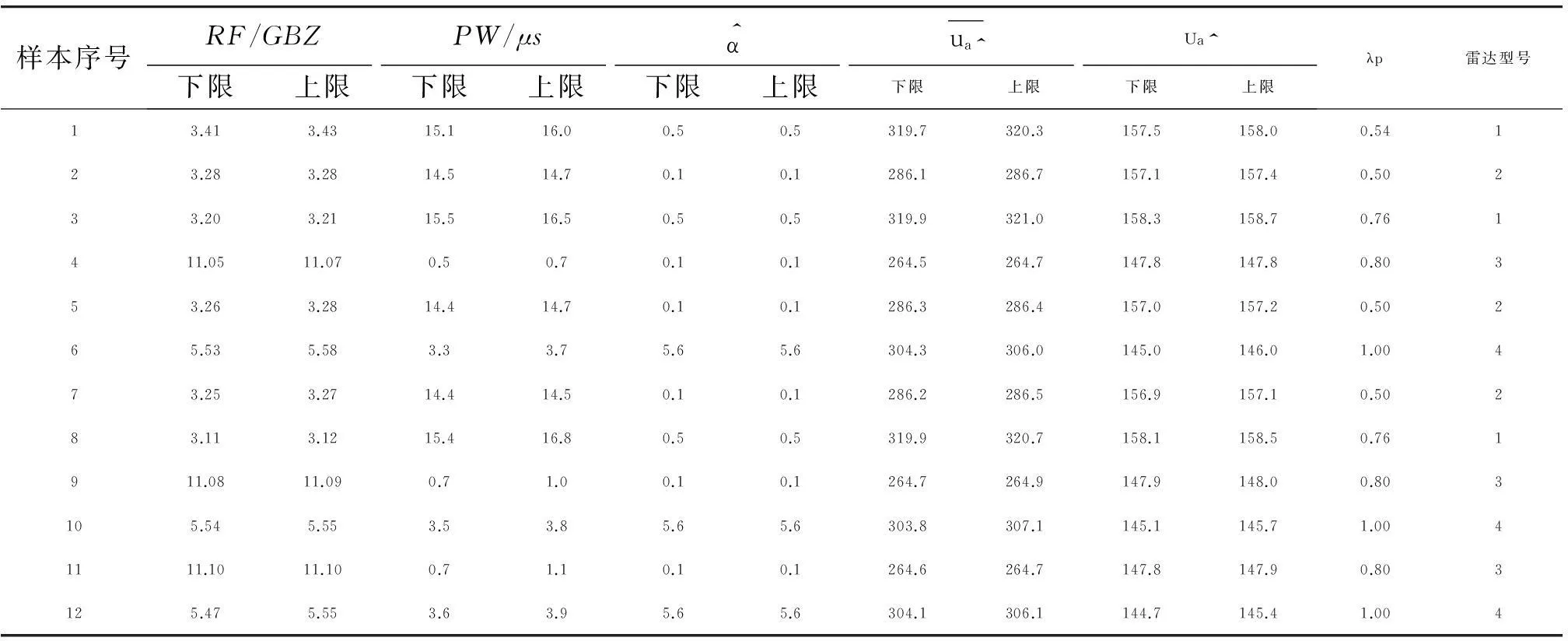
表2　样本数据及样本可信度计算结果

5-13-7的结构，学习速率η=0.01，惯性系数α=0.7，收敛误差Emax=0.05；平面变换因子PTF设置规则见表1。

表3　仿真雷达数据及PTF取值

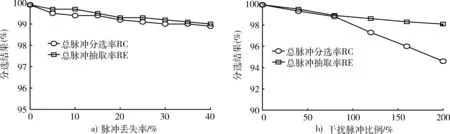
图4　平面变换分选效果Fig.4　Performance of pane transformation

将NCPT的分选结果与PRI关联法、多参数匹配法及脉冲样本图法3种算法进行比较，实验结果见表4。可见，3种现有算法中，脉冲样本图法的分选准确率最高，为88.5%，仍低于NCPT方法约9%；PRI关联法的脉冲抽取率为73.0%，高于多参数匹配法和脉冲样本图法，但远低于NCPT方法的99.1%。在处理速度上，通过100次蒙特卡罗实验得到脉冲数与处理时间的关系如图5所示，易见，NCPT方法在高脉冲密度条件下更容易满足实时性的要求。

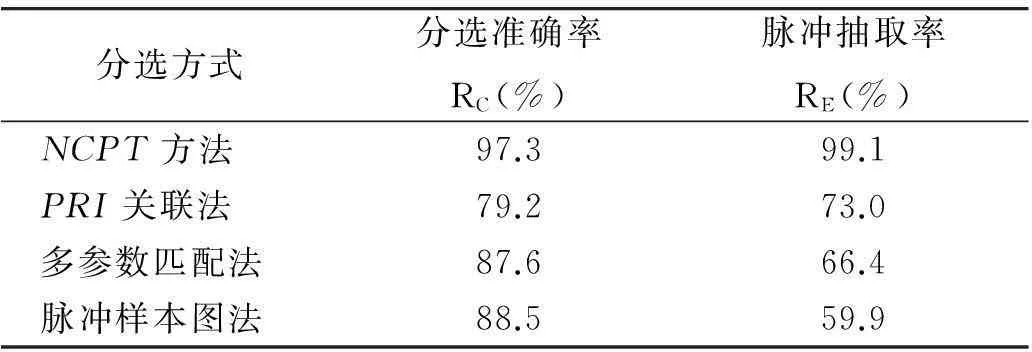
表4　不同分选方法效果比较

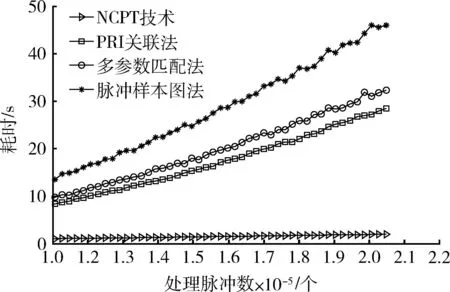
图5　处理时间与脉冲个数关系Fig.5　Processing time and the pulse number

3结论

对电磁环境中已知辐射源信号的预先分选可以大大提高信号分选的速度和准确度，但现有的预分选方法存在对脉冲丢失敏感，脉冲序列提取不完整等问题。本文提出的非线性分类器结合平面变换的分选方法，采用改进的矢量神经网络作为分类器，通过平面变换完成对脉冲串抽取，仿真实验验证了NCPT的有效性和可行性。得到结论如下：

(1) 利用熵权值后向矢量传播算法(EWVTBP)的矢量神经网络可有效完成对单脉冲的非线性分类，其识别率和容错性能均高于传统的NVTBP算法。

(2) 通过调用平面变换因子PTF，平面变换抽取算法可快算准确的提取出属于一部雷达的完整脉冲序列，且具有良好的抗干扰脉冲性能，几乎不受脉冲丢失的影响。

(3)NCPT方法相比于现有的对已知雷达分选方法，无论是在脉冲分选准确率、脉冲抽取率还是在处理时间上，均有较为明显的优势。

参考文献：

[1]ELBIRTAJ.InformationWarfare:AreYouatRisk[J].IEEETechnologyandSocietyMagazine, 2003, 22(4): 13-19.

[2]HASSANHE，CHANF，CHANYT．AdaptiveDeinter-LeavinginDenseESMSystemEnvironments[C]∥TheThirdInternationalConferenceonElectricalEngineering．Carlo，Egypt：MilitaryTechnicalCollege，2002．

[3]杨学永，宋国栋，钱轶，等. 现代雷达信号分选跟踪的几种方法[J]. 现代雷达，2014, 36(3): 43-48.

YANGXue-yong，SONGGuo-dong，QIANYi,etal.SeveralMethodsofRadarSignalSortingandTracking[J].ModernRadar, 2014,36(3): 43-48.

[4]ELTONSD．ACross-CorrelationTechniqueforRadarEmitterRecognitionUsingPulseTimeofArrivalInformation[C]∥Proc．ofDefenceApphcalionsofSignalProcessingWorkshop．BarossaValley，SouthAustralia：[s.n.]，2002．

[5]刘旭波，司锡才. 雷达信号分选实现的新方法[J]. 系统工程与电子技术，2010,32(1): 53-56.

LIUXu-bo,SIXi-cai.NewMethodforSortingRadarSignals[J].SystemsEngineeringandElectronics, 2010,32(1): 53-56.

[6]孟祥豪，罗景青. 基于合成特征参数和脉冲样本图的雷达信号分选[J]. 火力指挥与控制，2012,37(9): 50-54.

MENGXiang-hao，LUOJing-qing.RadarSignalSortingBasedonCompositiveCharacteristicParameterandPulsePattern[J].FireControl&CommandControl, 2012,37(9): 50-54.

[7]张国柱，姜文利，周一宇. 基于神经网络的辐射源识别系统设计[J]. 系统工程与电子技术，2004,26(2): 269-272.

ZHANGGuo-zhu,JIANGWen-li,ZHOUYi-yu.RadiatorIdentificationSystemBasedonNeuralNetworks[J].SystemsEngineeringandElectronics, 2004,26(2): 269-272.

[8]郑子扬，陈永游，张君，等. 基于SOFM网络聚类雷达信号分选预处理改进算法[J]. 航天电子对抗，2013,29(3): 42-50.

ZHENGZi-yang，CHENYong-you，ZHANGJun,etal.AnImprovedPre-ProcessingAlgorithmofRadarSignalSortingBasedonSOFMClustering[J].AerospaceElectronicWarfare, 2013,29(3): 42-50.

[9]周玉，朱安福，周林，等. 一种神经网络分类器样本数据选择方法[J]. 华中科技大学:自然科学版，2012，40(6)：39-43.

ZHOUYu,ZHUAn-fu,ZHOULin,etal.SampleDataSelectionforNeuralNetworkClassifiers[J].HuazhongUniv.ofSci. &Tech：NatureScienceed, 2012，40(6)：39-43.

[10]SHIEHC，LINC．AVectorNeuralNetworkforEmitterIdentification[J]．IEEETransactionsonAntennasandPropagation, 2002, 50(8): 1120-1127．

[11]刘海军，柳征，姜文利，等. 基于云模型和矢量神经网络的辐射源识别方法[J]. 电子学报，2010,38(12):2797-2799.

LIUHai-jun，LIUZheng，JIANGWen-li，etal.ApproachBasedonCloudModelandVectorNeuralNetworkforEmitterIdentification[J].ActaElectronicaSinica, 2010,38(12):2797-2799.

[12]IgorAizenberg,ClaudioMoraga.MultilayerFeedforwardNeuralNetworkBasedonMuti-ValuedNeurons(MLMVN)andaBackpropagationLearningAlgorithm[J].SoftComput,2007， 11: 169-183.

[13]樊甫华，张万军，谭营. 基于累积变换的周期性对称调制模式的快速自动搜索算法[J]. 电子学报，2005,33(7): 1266-1270.

FANFu-hua，ZHANGWan-jun，TANYing.AFastandAutomaticSearchingAlgorithmofPeriodicandSymmetricPatternsBasedonAccumulativeTransformationTechnique[J].ActaElectronicaSinica, 2005,33(7): 1266-1270.

[14]张西托，饶伟，杨泽刚，等. 平面变换技术脉冲分选自动实现方法[J]. 数据采集与处理，2012,27(4): 496-500.

ZHANGXi-tuo,RAOWei,YANGZe-gang,etal.AutomaticFulfillmentofDeinterleavingPulsesBasedonPlaneTransformation[J].JournalofDataAcquisition&Processing, 2012,27(4): 496-500.

[15]普运伟，金炜东，朱明，等. 雷达辐射源信号模糊函数主脊切面特征提取方法[J]. 红外与毫米波学报，2008,27(2): 133-137.

PUYun-wei,JINWei-dong，ZHUMing，etal.ExtractingtheMainRidgeSliceCharacteristicsofAmbiguityFunctionforRadarEmitterSignals[J].InfraredMillimWaves, 2008,27(2): 133-137.

Approach Based on Nonlinear Classifiers and Plane TransformationforRadarSignalDeinterleaving

LIU Zhi-peng, ZHANG Guo-yi，TIAN Run-lan

(Aviation University of Air Force, Jilin Changchun 130022, China)

Abstract:Aiming at the fact that the existing methods for known radar deinterleaving has disadvantage of low speed of identification, low efficiency, sensitive to pulse missing and sequence extracting incompletely, a new radar signal deinterleaving method called nonlinear classifiers and plane transformation is proposed. This technology firstly extracts the features including radio frequency, pulse width and intra-pulse modulation and so on, which are presented to nonlinear classifiers to achieve the identification of emitter for single pulse, then the corresponding parameters got by identification results are utilized to conduct the plane transformation which come true the extraction of the pulse train. Simulation experiments show that this method has advantage of fast speed, high accuracy, easy to implement, etc.

Key words:radar; signal deinterleaving; nonlinear classifier; plane transformation;vector neural network

*收稿日期：2015-04-30；修回日期：2015-12-02

作者简介：刘志鹏(1990-)，男，吉林长春人。硕士生，主要从事电子情报处理。

通信地址：130022吉林省长春市南湖大路2222号学员11队E-mail：1179283747@qq.com

doi:10.3969/j.issn.1009-086x.2016.03.021

中图分类号：TN957.52

文献标志码：A

文章编号：1009-086X(2016)-03-0127-07