基于可变增益的动力翼伞反步降高控制

陈自力 张 昊 邱金刚 苏立军

军械工程学院无人机工程系，石家庄050003



基于可变增益的动力翼伞反步降高控制

陈自力 张 昊 邱金刚 苏立军

军械工程学院无人机工程系，石家庄050003

针对无人动力翼伞稳定航速下的降高控制问题，提出一种基于可变增益的自适应反步控制策略。根据翼伞纵向模型推导了稳定航速下尾沿偏转反步控制律，并通过对增益参数的合理设计，消除了控制律中的复杂非线性项，避免了传统反步法中虚拟量的复杂导数问题，使控制器具有简单的参数可调节形式。利用模糊逻辑系统对可变增益参数进行在线调节，优化了控制器性能。将控制器应用于外部干扰条件下的动力翼伞降高控制中，结果表明控制器具有较小的稳态误差和较高的跟踪精度。

无人动力翼伞；可变增益；反步法；降高控制；模糊系统

无人动力翼伞(Unmanned Powered Parafoil, UPP )作为一种新型无人飞行系统，以其优秀的飞行性能和在侦察监视、物资投送和防火治霾等任务中的应用优势，逐渐成为无人软翼飞行器领域的研究热点[1]。UPP仅对翼伞空投系统的结构稍加改进，增加了以螺旋桨为主的动力装置，增强了高度与速度的可控性以及姿态的灵活性，扩展了其应用空间，因此，纵向通道的高度控制是UPP不同于空投系统的特殊控制问题。

目前高度控制主要依靠改变推力的方式，该方式在起飞与爬升阶段具有一定优势，但在降高过程中，存在跟踪精度不高，姿态稳定性差的缺陷。针对以上问题，研究人员提出了一些降高控制方法。Gideon[2]建立了对象六自由度线性化模型，并对两通道PD控制方法进行了研究和验证。Chrystine[3]分析了不同自由度模型对PID控制器控制精度的影响，并提出了增稳方案。Michael[4]提出了基于翼伞尾沿偏转的可变迎角自适应滑翔率控制策略，并进行了相应的实验研究。Alex[5]采用上下翼面增加扰流切口的方式，提高了尾沿偏转的气动效率，提高了控制的有效性。Formal'skii[6]和Yang[7]等建立了翼伞非线性模型，研究了结构参数、马力以及尾沿下偏量对纵向运动性能的影响，为控制策略研究提供了模型基础。国内对这一领域研究起步较晚，张兴会[8-9]针对翼伞系统降落过程建立了六自由度模型，设计了PID控制器，对航迹跟踪过程中的纵向误差进行了有效修正。以上研究中，基于改进物理结构的方法增加了系统的可控性，但对所增加的控制通道缺乏系统的控制策略；基于线性化模型的控制方法具有局限性，当模型在实际运动中表现为非线性特性时，无法保证系统的稳定性。

为克服上述线性控制方法的不足，提出了一些非线性控制方法，比如反馈线性化、动态逆和反步法等。其中，反步法在此方面发展较快，其原理是通过构造Lyapunov函数，逐层递推并设计虚拟控制量实现对前一层系统的镇定，然而，反步法递推过程中需不断对虚拟控制量进行求导，当系统阶数较高时，计算过程变得非常繁琐[10]。

本文以无人动力翼伞纵向模型为对象，针对反步控制方法存在的缺陷，提出了一种基于可变增益的自适应反步控制策略。首先，基于反步法和Lyapunov稳定性思想，推导了尾沿偏转反步控制律，通过合理设计增益参数消除了控制器中的部分非线性项，避免了对虚拟控制量多次求导后的复杂形式，减少了可调增益个数，简化了控制器结构；然后，采用模糊逻辑系统对增益参数进行在线调节；最后，将所提算法应用于不同初始状态和外界干扰条件下的降高控制中，仿真结果验证了控制器的有效性。

1 UPP纵向平面模型

不考虑橫侧面滚转运动，在稳定航速uc下，采用尾沿下偏进行降高控制，UPP纵平面动力学方程为

(1)

其中：

(2)

式中，系统状态量[qw]T分别为俯仰角速度q和纵向速度w；u为前向速度；m表示UPP质量，mq和mw分别表示翼伞绕机体轴作俯仰运动和沿机体轴作垂向运动时，流体产生的附加质量；M(·)为气动力参数；Ιy为绕y轴的转动惯量；G为重力；δa为尾沿下偏产生的纵向控制力矩；Δτ表示有界扰动项和与系统状态相关的模型不确定性。

假设进行稳定航速下的低空降高控制，纵向速度w相对于前向速度u较小，可以忽略，运动学方程可简化为：

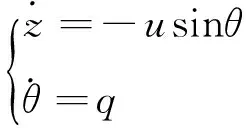
(3)

式中，系统状态量[zθ]T分别为飞行高度与俯仰角。

2 控制器设计

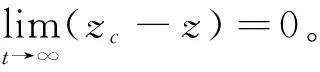
2.1 可变增益反步控制方法

Step1 定义高度误差ze=zc-z，构造如下Lyapunov函数

(4)

求导，并将式(3)代入(4)得

(5)

k1=-l1ze,l1>0

(6)

对式(5)进行变换，并将式(6)代入式(7)，整理得

(7)

定义

θe=θ-k1

(8)

Step2 结合式(4)，构造Lyapunov函数

(9)

式中，c1>0，对上式两边求导，将式(7)代入得

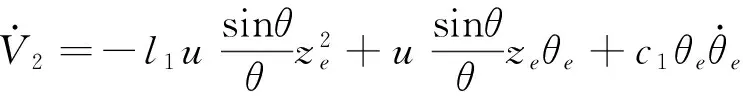
(10)

由式(8)可得

(11)

将上式代入式(10)，得

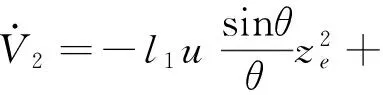
(12)

进一步，由θ=θe+k1，式(12)可变换为

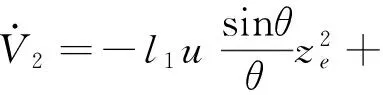
(13)

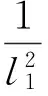
(14)

此时设计俯仰角速度虚拟控制量k2为

k2=-l2θe,l2>0

(15)

将式(15)代入式(14)得

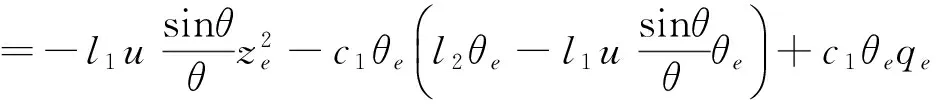
(16)

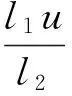
Step3 结合式(9)，构造如下Lyapunov函数

(17)

式中,c2>0，对上式求导，并将式(16)代入得

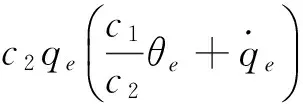
(18)

由式(15)可得

(19)

将上式代入式(18)得

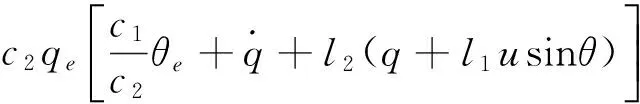
(20)

根据UPP动力学模型式(1)和(3)，最终控制输入可表示为

(21)

式中，l3>0，将控制输入代入式(20)得

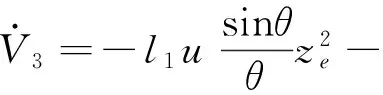
(22)

将式(21)中间变量替换为系统状态变量得

δa=-mq(p1ze+p2θ+p3q)-
(mql1l2sinθ+Δτ)

(23)

式中，

(24)

由式(21)可以看出，控制输入中仅有一项为非线性项，其余均为系统状态的线性组合，具有简单的增益调节形式。

为了进一步说明所提方法的有效性，现采用传统反步法设计控制器[11]，最终控制输入为：

δa=-mq[(β1β2β3+β3u)zesecθ+sinθcosθ+
(β1u+β2)·qtan2θ+(β1u+β2+β3)q+
(u+β1β2)qzesinθsec2θ+β1zecosθ+
(u2+β1β2u+β1β3u+β1β3)tanθ-Δτ]

(25)

式中，βi>0为控制器增益系数。

对比控制输入式(23)与(25)可以看出，相比于传统反步法，所提方法具有更简单的结构形式，更有利于工程实现。

2.2 增益参数调节

由所设计控制器式(23)可以看出，控制输入中仅包含一项非线性项，其余均为系统状态的线性函数组合，具有明显的PID参数组合形式，因此可借鉴PID参数调节方法，采用模糊策略对增益参数(p1,p2,p3)进行在线调节，优化控制器性能。

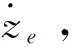
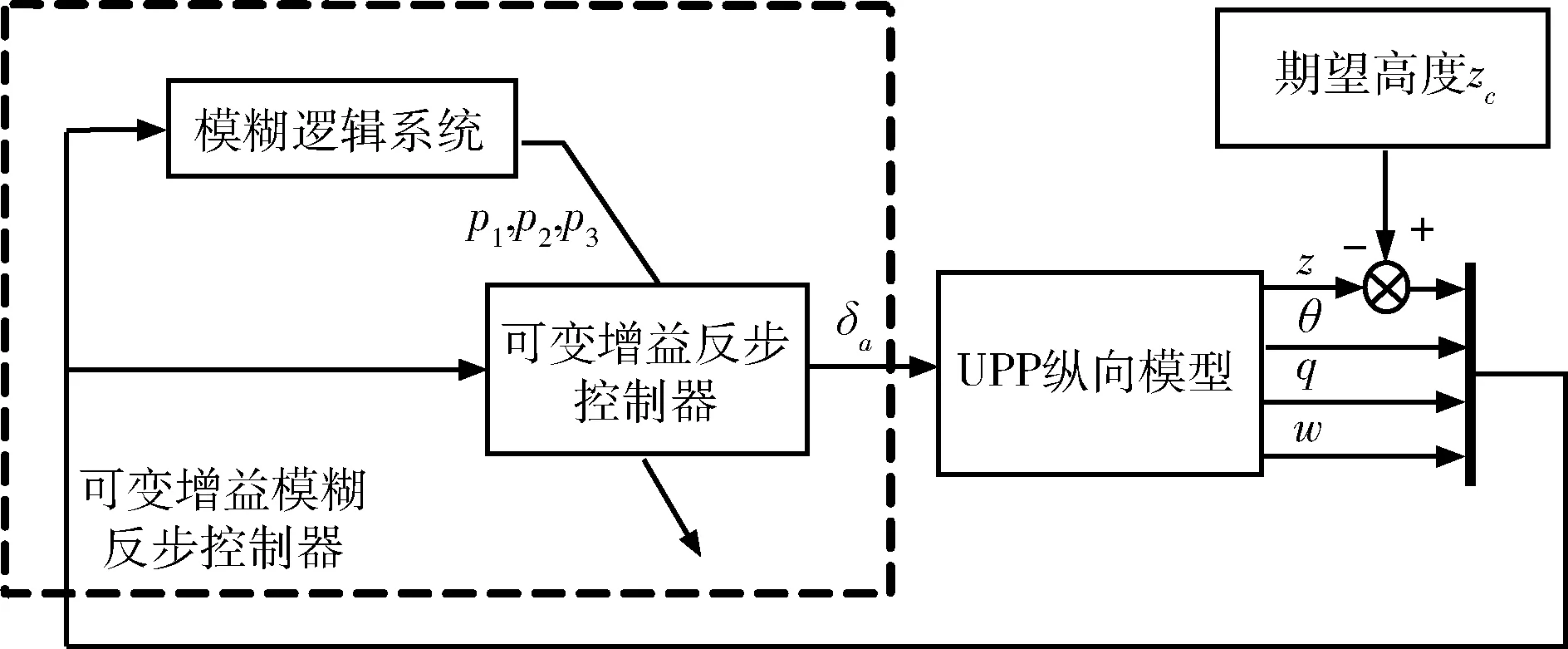
图1 控制器结构框图

3 仿真分析

以实验室自行设计改造的试验型无人动力翼伞为研究对象，建立动力学模型，其结构参数如表1所示，气动参数参考不同展弦比翼伞辨识数据[13]，采用本文提出的可变增益反步控制器进行降高控制，分别对不同初始条件和存在外部干扰时的控制效果进行仿真分析。

在含有干扰作用条件下对所提方法进行仿真分析。设定高度变化如式(26)，初始状态为[zθqw]T=[50 0 0 0]T，初始增益参数

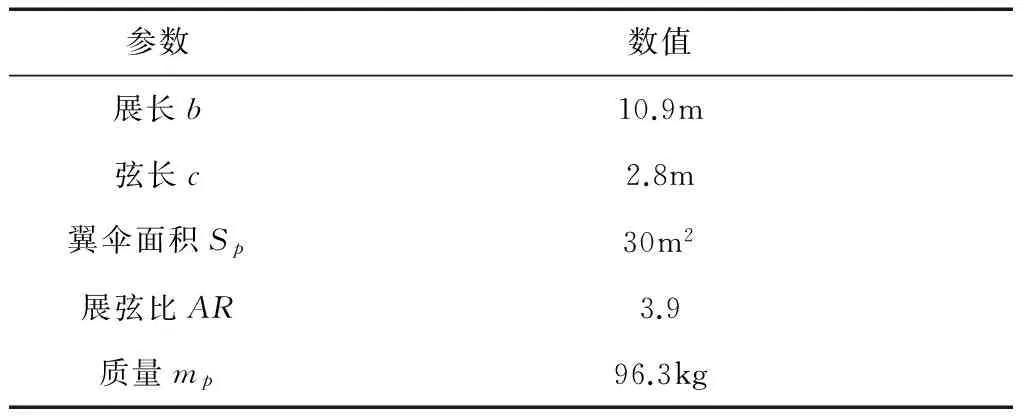
表1 UPP主要结构参数

为p1=0.06，p2=0.5，p3=20，仿真过程中加入式(27)所示的干扰作用，

(26)

Δτ=5sin(0.03πt)+3w+5q

(27)

图2比较了含有外界扰动情况下可变增益模糊反步控制器与自适应PID及传统反步法的高度跟踪情况。图中可见，PID控制器在遇到外界干扰作用时效果变差，无法实现对时变扰动的抑制，控制输入容易陷入饱和区，无法保证跟踪精度，而本文提出的方法具有自适应机制，能够对扰动进行补偿，保证了跟踪性能，且相比于传统反步法，对参数摄动的适应性更强，响应速度更快。在图3～4中对3种方法的控制输入和系统状态做比较，且由图4的状态变化可以看出，系统纵向速度相对于前向速度很小，设计控制律时可以忽略。图5为增益参数调节曲线，优化后的增益值为p1=0.063，p2=0.505，p3=12.9。

图2 高度控制曲线

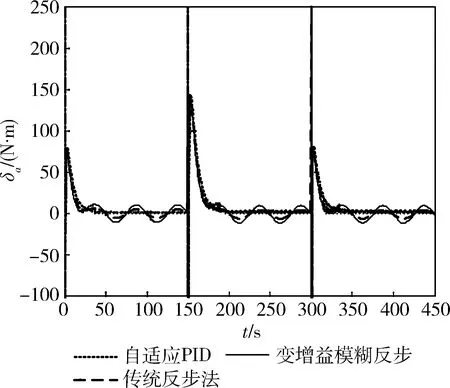
图3 控制输入曲线

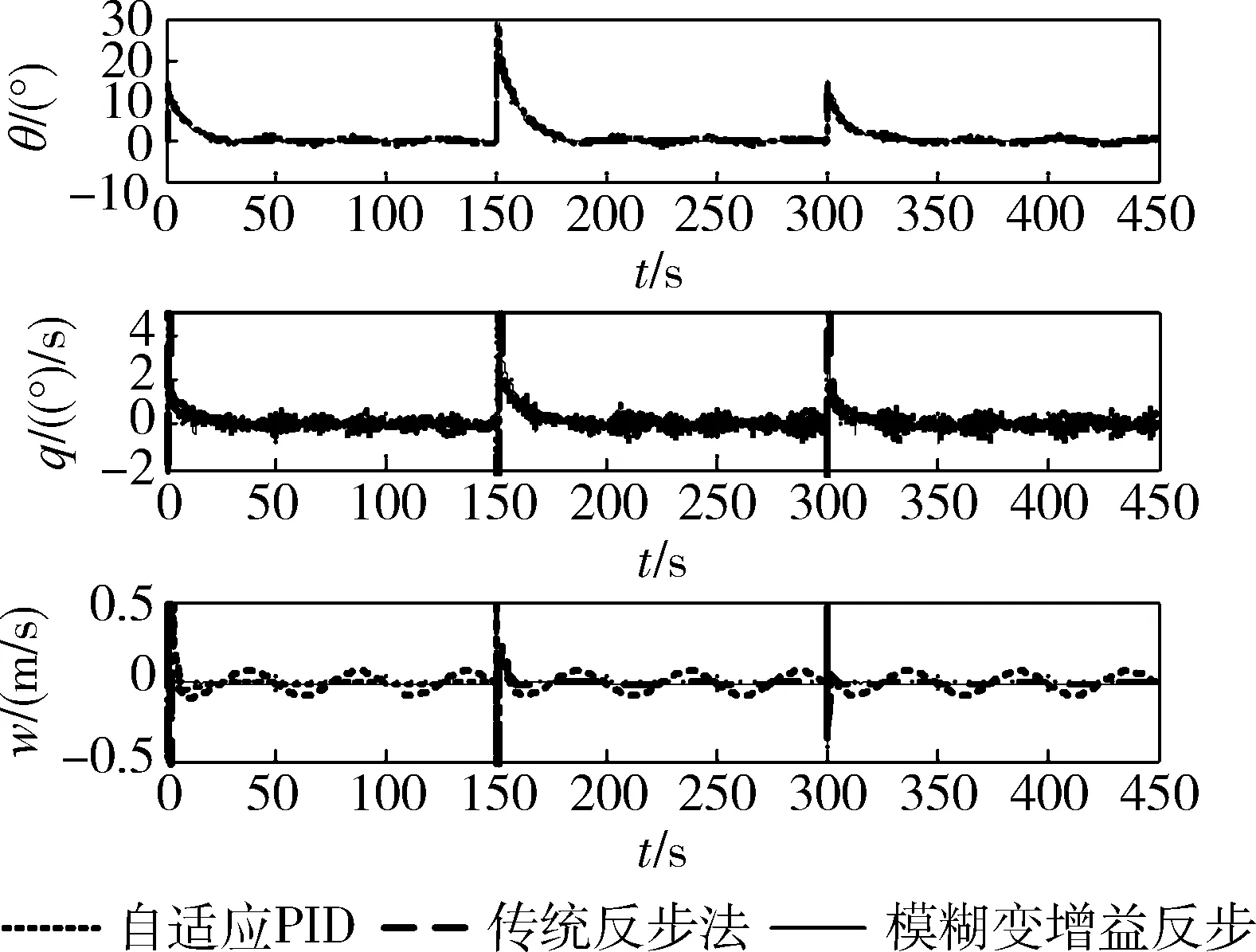
图4 系统状态响应曲线

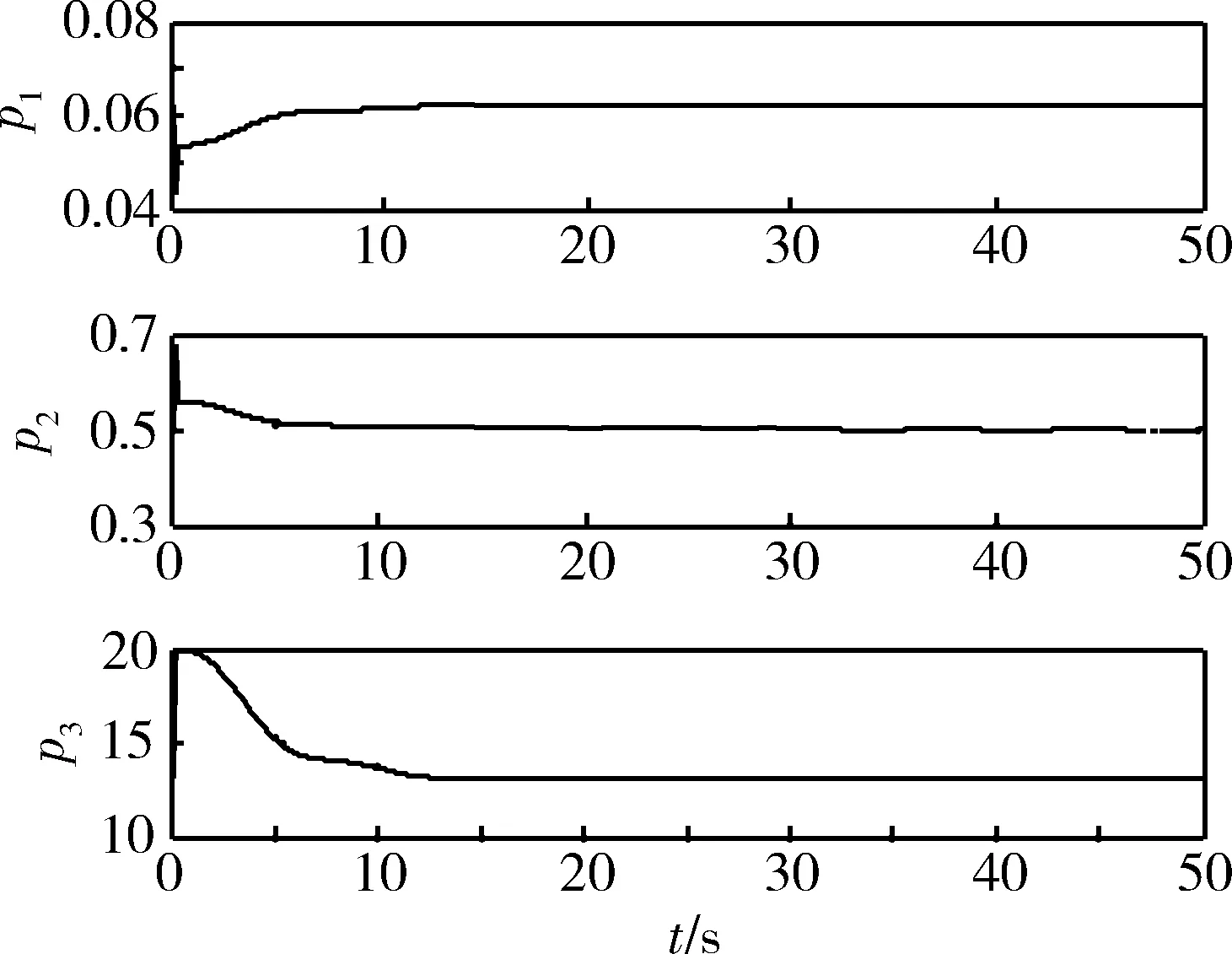
图5 增益参数调节曲线

4 总结

针对无人动力翼伞稳定航速下的降高控制问题，提出了一种基于可变增益的自适应模糊反步控制方法。根据系统数学模型逆向反推构建了高度控制器，通过合理设计控制参数，避免了传统反步法中虚拟量的复杂导数问题，控制器具有更简单的形式，并采用模糊逻辑系统对控制器增益进行在线调节。针对不同初始状态和外部干扰条件下的控制效果进行了仿真实验，结果表明，所提方法与自适应PID及传统反步法相比具有较小的稳态误差和较高的跟踪精度，适合于UPP的自主降高控制。

[1]LiuH,GuoL,ZhangY.AnAnti-DisturbancePDControlSchemeforAttitudeControlandStabilizationofFlexibleSpacecrafts[J].NonlinearDynamics, 2012, 67(3): 2081-2088.

[2]GideonK.FlightControlSystemforAnAutonomousParafoil[D].Stellenbosch:StellenboschUniversity, 2013.

[3]ChrystineM,SlegersN.EvaluationofMultibodyParafoilDynamicsUsingDistributedMiniatureWirelessSenors[J].JournalofAircraft, 2012, 49(2): 546-555.

[4]MichaelW,AlekG,MarkC.GlideSlopeControlAuthorityforParafoilCanopieswithVarialeIncidenceAngle[J].JournalofAircraft, 2013, 5(5): 1504-1513.

[5]AlekG,MichaelW,CostelloM.ParafoilControlAuthoritywithUpper-SurfaceCanopySpoilers[J].JournalofAircraft, 2012, 49(5): 1391-1397.

[6]Formal'skii.MathematicalModelingofControlledLongitudinalMotionofaParaglider[J].ComputationalMathematicsandModeling, 2013, 24(3): 418-431.

[7]YangH,LiuC.StudyonPowered-ParafoilLongitudinalFlightPerformancewithaFastEstimationModel[J].JournalofAircraft, 2013, 50 (5): 1660-1667.

[8] 张兴会,朱二琳. 翼伞系统雀降性能及控制研究[J]. 航天控制, 2012, 30(1): 29-32,39.(ZhangXinghui,ZhuErlin.TheStudyoftheFlare-LandingPerformanceandControlofParafoilSystem[J].AerospaceControl, 2012, 30(1): 29-32,39.)

[9] 张兴会,朱二琳. 基于能量约束的翼伞系统分段归航设计与仿真 [J]. 航天控制, 2011, 29(5), 43-47.(ZhangXinghui,ZhuErlin.DesignandSimulationintheMultiphaseHomingofParafoilSystemBasedonEnergyConfinement[J].AerospaceControl, 2011, 29(5): 43-47.)

[10] 贾鹤鸣, 宋文龙, 陈子印. 基于自适应反步法的自主水下航行器变深控制[J]. 控制理论与应用, 2013, 41(1): 15-20. (JiaHeMing,SongWenLong,ChenZiYin.DivingControlofAutonomousUnderwaterVehicleBasedonAdaptiveBacksteppingMethod[J].ControlTheory&Applications, 2013, 41(1): 15-20.)[11] 胡云安, 晋玉强, 李海燕. 非线性系统鲁棒自适应反演控制[M]. 北京: 电子工业出版社, 2010:158-164.(Hu Yunan, Jin YuQiang, Li HaiYan. Robust of Adaptive Backstepping Control for Nonlinear Systems [M]. Beijing: Publishing House of Electronics Industry, 2010:158-164.)

[12] 佟绍成. 非线性系统的自适应模糊控制[M]. 北京: 科学出版社, 2010.(Tong ShaoCheng. Adaptive Fuzzy Control of Nonlinear System [M]. Beijing: Science Publishing House, 2010.)

[13] Majeed M, Jatinder S. Identification of Aerodynamic Derivatives of a Flexible Aircraft [J]. Journal of Aircraft, 2012, 49(2): 654-658.

The Backstepping Altitude Reduction Control of Powered ParafoilBased on Variable-Gain

Chen Zili， Zhang Hao, Qiu Jingang, Su Lijun

Department of UAV Engineering, Ordnance Engineering College, Shijiazhuang 050003，China

Todealwiththealtitudereductioncontrolproblemofunmannedpoweredparafoil(UPP)underastablevelocity,anadaptivebacksteppingcontrolapproachisdeveloped,whichisbasedonvariable-gain.Thebacksteppingcontrolstrategyoftrailingedgedeflectionwithvariable-gainisproposedunderastablevelocitybasedonthelongitudinalmodelofUPP,andthenonlineartermiseliminatedbychoosingthecontrollerparametersreasonably.Andtherequirementofthecomplicatedderivativeofvirtualcontrolvariableintraditionalbacksteppingmethodisavoided,whichsimplifiestheparameteradjustmentofcontroller.Thegainparameterisadjustedonlinebythefuzzylogicsystemwhichoptimizesthecontrollerperformance.SimulationexperimentisimplementedforthecontrollerappliedtoUPPreducingheightcontrolwithexternaldisturbances,theresultsvalidatethesmallsteady-stateerrorandtheaccuratetrackingability.

Unmannedpoweredparafoil;Variable-gain;Backstepping;Altitudereduction;Fuzzysystem

2015-10-08

陈自力(1964-)，男，山西运城人，教授，主要研究方向为无人机导航、制导与控制；张 昊(1988-)，男，山西临汾人，博士研究生，主要研究方向为无人机控制理论与应用；邱金刚(1979-)，男，洛阳人，硕士，讲师，主要研究方向为无人机控制技术；苏立军(1981-)，男，石家庄人，硕士，讲师，主要研究方向为无人机系统一体化设计。

TP273

A

1006-3242(2016)03-0003-05