伺服机械系统共振模态的数值仿真方法研究*
2016-07-20季冬冬刘红俐朱其新朱永红
季冬冬 刘红俐 朱其新 朱永红
1. 苏州科技学院,苏州215009 2. 景德镇陶瓷学院,景德镇333001
伺服机械系统共振模态的数值仿真方法研究*
季冬冬1刘红俐1朱其新1朱永红2
1. 苏州科技学院,苏州215009 2. 景德镇陶瓷学院,景德镇333001

在进行高精度伺服控制系统的设计时,闭环仿真环节必不可少。要进行伺服系统的闭环仿真,就必须考虑该共振模态的数学模型。本文首先介绍了伺服机械系统共振模态的数学模型, 其可以看成由一个二阶微分环节和一个振荡环节相乘得到。其次,提出用一个二阶微分环节来仿真共振模态中的反共振部分,用一个振荡环节来仿真共振模态中的共振部分。最后,给出了一个共振模态的数值仿真实例。
共振模态;数值仿真;微分环节;振荡环节;伯德图
伺服系统(Servomechanism)又称随动系统,是用来精确地跟随或复现某个过程的反馈控制系统。伺服系统是使物体的位置、方位、状态等输出被控量能够跟随输入目标(或给定值)任意变化的自动控制系统。它的主要任务是按控制命令的要求,对功率进行放大、变换与调控等处理,使驱动装置输出的力矩、速度和位置控制非常灵活方便。在很多情况下,伺服系统专指被控制量(系统的输出量)是机械位移或位移速度、加速度的反馈控制系统,其作用是使输出的机械位移(或转角)准确地跟踪输入的位移(或转角),其结构组成和其他形式的反馈控制系统没有原则上的区别。伺服系统最初用于国防军工, 如火炮的控制, 船舰、飞机的自动驾驶,导弹发射等,后来逐渐推广到国民经济的许多部门,如自动机床、无线跟踪控制和半导体生产设备等[1-5]。
机械共振是伺服控制中的常见难题之一,其通常是由2个惯性物体间的弹性部分引起的。其中,最常见的是由马达和负载之间的传动装置的弹性引起的,共振是指机械系统所受激励的频率与该系统的某阶固有频率相接近时,系统振幅显著增大的现象。共振时,激励输入机械系统的能量最大,系统出现明显的振型称为位移共振。此外还有在不同频率下发生的速度共振和加速度共振。
机械共振中常见的激励有直接作用的交变力、支承或地基的振动与旋转件的不平衡惯性力等。共振时的激励频率称为共振频率,近似等于机械系统的固有频率。对于单自由度系统,共振频率只有一个。对于多自由度线性系统,有多个共振频率。对于非线性系统,共振区出现振幅跳跃现象,共振峰发生明显变形,并可能出现超谐波共振和次谐波共振。共振时激励输入系统的功同阻尼所耗散的功相平衡,共振峰的形状与阻尼密切相关。大多数情况下共振是有害的,会引起机械和结构很大的变形和动应力,甚至造成破坏性事故。从机械的角度,防共振有如下措施:改进机械的结构或改变激励,使机械的固有频率避开激励频率;采用减振装置;机械起动或停车过程中快速通过共振区。从控制的角度,减少共振对系统的影响常采用带阻滤波器[6]。
进行高精度伺服控制系统的设计时,闭环仿真环节必不可少,而进行伺服系统的闭环仿真,就必须考虑该共振模态的数学模型,如果不考虑共振模态的影响,则所得到的闭环仿真结果会与实际伺服系统有较大差别。所以研究共振模态的数值仿真具有重要意义,但国内外尚未见关于机械共振模态的数值仿真方法的研究报道。本文在分析共振模态数学模型的基础上,将共振模态看成由一个二阶微分环节和一个振荡环节相乘,并提出用一个微分环节来仿真共振模态中的反共振部分,用一个振荡环节来仿真共振模态中的共振部分。
1 共振模态的数学模型
多数情况下共振由电机与负载之间的柔性引起,如图1所示。事实上,所有的传输元件都有一个弹性系数,多个弹性系数加在一起就构成了电机与负载之间的弹性连接[7]。

图1 电机与负载之间的柔性示意图
其中,TE为转矩,AM为电机的加速度,VM为电机的速度,PM为电机的位置,AL为负载的加速度,VL为负载的速度,KS为位置弹性系数。当电机轴开始旋转时,耦合的传输弹性(这里用KS来表示)会收紧,并在负载上产生一个转矩,该转矩与电机和负载的位置差或速度差成比例,其中与电机和负载的位置差成比例的转矩称为弹性转矩,与电机和负载的速度差成比例的转矩称为阻尼转矩;电机产生的驱动负载的转矩也会反传回来,从而降低了电机的速度。
由文献[6-7]可知,当伺服系统只具有一个共振模态时,其共振模态可表示如下:

(1)
其中,JM是伺服电机的转动惯量,JL是负载的转动惯量,KS是位置弹性系数,KCV是速度弹性系数。在低频时,由于s很小,共振模态接近单位1,换句话说,在低频时弹性耦合对系统影响很小,其波特图如图2所示。
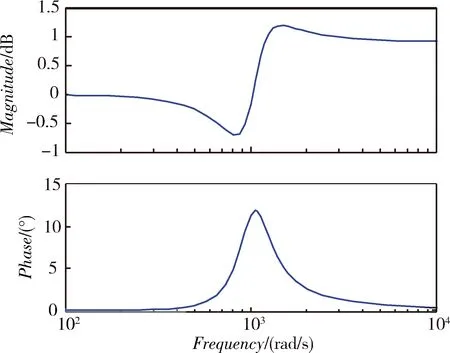
图2 伺服系统共振模态的波特图
2 共振模态的数学模型的数值仿真实现
在进行闭环伺服系统仿真时,式(1)中的KC和KCV很难知道,对这2个参数用户也可以不关心,所关心的是共振频率wR、共振幅值MR、反共振频率wAR和反共振幅值MAR。有了这4个参数,便可以设计如式(1)所示的共振模态。在进行共振模态的仿真时,可考虑模型:

(2)
现在的问题是如何设置式(2)中的待定系数ξ1,ξ2,wn1,wn2,使L(s)的频率特性与期望的频率特性一致,即其频率特性具有共振频率wR、共振幅值MR、反共振频率wAR和反共振幅值MAR。
为设计式(2)中的待定系数,不妨先考察式(2)中的振荡环节

(3)
在ξ2=0.02,wn2=200πrad/s时,ZD(s)的频率特性如图3所示。

图3 典型振荡环节的波特图
该波特图明显存在一个谐振,目的是用该谐振峰值M2来产生共振模态中的共振幅值MR。容易证明,该振荡环节的谐振频率发生在Wr2处,且其谐振峰值M2与阻尼比ξ2的关系如下[8]:
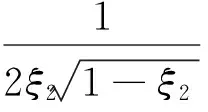
(4)

(5)
如果已知谐振峰值来反求所需要的阻尼比,式(4)改写为式(6)便可

(6)
但式(4)和(6)中谐振峰值的单位都不是dB,如果已知共振幅值MR(单位为dB)来求合适的阻尼比,则应先将共振幅值变换为对应的谐振峰值,变换公式如下:
(7)
将式(7)代入(6)可得

(8)
在伺服系统中,当共振模态的共振幅值较小时,其对系统影响很小,可以不去考虑。需要考虑的共振模态的共振幅值一般都比较大,所以由式(8)可知,此时的阻尼比ξ2小。
再由式(5)可知,当ξ2很小时有
wr2≈wn2
(9)
在进行共振模态的仿真时,可以简单地认为谐振频率为wn2。所以当共振频率wR和共振幅值MR给定时,便可以确定ξ2和wn2,也即确定了式(3)所示的振荡环节的模型。
再来考察式(2)中的二阶微分环节
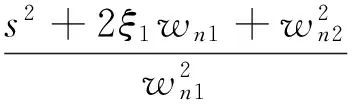
(10)
在ξ1=0.03,wn2=140πrad/s时,WF(s)的频率特性如图4所示。
该波特图明显存在一个反谐振,目的是用该反谐振峰值M1来产生共振模态中的反共振幅值MAR。容易证明,该振荡环节的谐振频率发生在wr1处,且其谐振峰值M1与阻尼比ξ1的关系如下[8]:

(11)

(12)

图4 典型二阶微分环节的波特图
但式(11)中的反谐振峰值的单位不是dB,如果已知反共振幅值MAR(单位为dB)来求合适的阻尼比,则应先将反共振幅值变换为对应的反谐振峰值,变换公式如下:
(13)
将式(13)代入(11)可得

(14)
由于反共振幅值MAR的数值为负,所以此时的阻尼比ξ1很小。再由式(12)可知,当ξ1很小时有
wr1≈wn1
(15)
在进行共振模态的仿真时,可以简单地认为反谐振频率为wn1。所以当反共振频率wAR和反共振幅值MAR给定时,便可以确定ξ1和wn1,也即确定了式(10)所示的二阶微分环节的模型。
在知道了对应的振荡环节和二阶微分环节的数学模型之后,将这2个环节的数学模型相乘,在波特图上表现为将这2个环节的波特图相叠加。当这2个环节的波特图叠加到一起时,这2个环节在共振频率和反共振频率处相互影响,按给定的MAR和MR设计的阻尼比ξ1和ξ2已不能满足要求,此时可以根据2个共振幅值误差的符号,通过循环的方式微调阻尼比ξ1和ξ2。微调的原则是:阻尼比越小,谐振幅值越大;阻尼比越大,谐振幅值越小。在循环程序内,逐渐微调阻尼比ξ1和ξ2,直到共振幅值和反共振幅值满足精度要求便可。
3 数值仿真示例
用本文的方法产生的反共振频率为250Hz,反共振幅值为20dB,共振频率为380Hz,共振幅值为20dB的共振模态的数学模型如式(16)所示。

(16)
该模型的波特图如图5所示。由图可以清楚地看到,在250Hz处有一个幅值为-20dB的反共振,在380Hz处有一个幅值为20dB的共振,与设计要求一致。

图5 共振模态的波特图
4 结论
在分析了伺服机械系统共振模态数学模型的基础上,提出用一个微分环节来仿真共振模态中的反共振部分,用一个振荡环节来仿真共振模态中的共振部分,从而实现了对单个共振模态的数值仿真。但在实际的伺服机械系统中往往存在多个共振模态,多个共振模态的数值仿真有待于进一步研究。
[1]ShenTL,JiaoXH,ZhangJY.Anadaptiveservocontrolstrategyforautomotiveelectronicthrottleandexperimentalvalidation[J].IEEETransactionsonIndustrialElectronics. 2014,61(11),6275-6284.
[2]ChenYS,MaoYL,ZhaoSH.Adaptiveloadobserver-basedfeed-forwardcontrolinPMSMdrivesystem[J].TransactionsoftheInstituteofMeasurementandControl. 2015,7(3), 414-424.
[3]DelpouxR,FloquetT.High-orderslidingmodecontrolforsensorlesstrajectorytrackingofaPMSM[J].InternationalJournalofControl. 2014, 87(10), 2140-2155.
[4]Taktak-MeziouM,ChemoriA,GhommamJ.LinearandnonlinearMPCfortrackfollowinginthedesignofHDDservosystems[J].InternationalJournalofSystems,ControlandCommunications. 2014, 6(1):20-47.
[5] Zhu Qixin, Xiong Lei. Higher order modeling of position loop plant and controller design in PMSM servo system [J]. Innovative Computing, Information and Control -Express Letters, Part B: Applications, 2015, 6(6): 1691-1696.
[6] 朱其新,刘红俐,Nokolay Krys. 伺服系统中一种新的带阻滤波器的设计[J].微计算机信息,2008,7(1): 56-58.(Zhu Qixin, Liu Hongli,Nokolay Krys. A new design of notch filter in servo systems[J]. Control & Automation, 2008,7(1): 56-58.)
[7] George Ellis. Control System Design Guide[Z]. Boston:Academic Press, 2000.
[8] 胡寿松.自动控制原理(第6版)[M]. 北京:科学出版社,2013.(Hu Shousong. Automatic Control Theory[M]. Beijing: Science Press, 2013.)
The Numerical Simulation Approach for Resonance Modes of Servo Mechanical System
Ji Dongdong1, Liu Hongli1, Zhu Qixin1, Zhu Yonghong2
1. Suzhou University of Science and Technology, Suzhou 215009, China 2. Jingdezhen Ceramic Institute, Jingdezhen 333001, China
Theclosedloopsimulationsarerequisitewhentheservocontrolsystemwithhighprecisionisdesigned.Themathematicalmodelofresonancemodemustbeconsideredwhentheclosedloopsimulationsofservosystemsareperformed.Firstly,themathematicalmodelofresonancemodeisintroducedinthispaper.Then,thismodelcanberegardasaproductofadifferentiationelementandanoscillatingelement.Thesecond-orderdifferentiationelementisproposedtosimulatetheresonantpartandtheoscillatingelementisproposedtosimulatetheanti-resonantpart.Finally,anumericalsimulationcasestudyofaresonancemodeisshown.
Resonancemode;Numericalsimulations;Differentiationelement;Oscillatingelement; Bodediagram
*国家自然科学基金(51375323,61164014,61563022);江西省自然科学重大基金(20152ACB20009);江苏省青蓝工程、苏州科技学院科研基金(XKZ201409);苏州科技学院大学生创新基金(2013067)
2015-09-21
季冬冬(1992-),男,江苏大丰人,本科,主要研究方向为机电控制;刘红俐(1972-),女,陕西米脂人,硕士,副教授,主要研究方向为伺服控制;朱其新(1971-),男,安徽定远人,博士,教授,主要研究方向为伺服控制与网络控制;朱永红(1963-),男,江西鄱阳人,博士,教授,主要研究方向为网络控制与信息融合。
TP15
A
1006-3242(2016)03-0073-04
