耦合的合成负反馈环路单参数分析

刘彩霞，毕小山

(河南理工大学，河南 焦作 454150)



耦合的合成负反馈环路单参数分析

刘彩霞，毕小山

(河南理工大学，河南 焦作 454150)

摘要：由于真实基因调控网络的复杂性,无论是定性还是定量分析都很难在系统水平上整体进行。然而,生物系统中存在大量的、相对独立的、具有特定生物功能的调控网络模块。比如正反馈环路、负反馈环路、前馈圈等。复杂的基因调控网络是由众多简单的调控环路所组成的,研究整合的简单调控环路的功能有助于进一步理解更复杂的真实网络的生物物理机制。本文主要研究了耦合的合成负反馈环路在整合之后所表现的振动、双韵律、硬激励等动力学功能。双韵律,即不同振幅和频率的振动在相同参数的模型中共同存在;硬激励,即在相同参数的模型中系统由于初值的不同可以表现为稳定的平衡态或稳定的周期轨。这两种动力学现象已经在生物实验中验证是真实存在的。

关键词：合成基因；基因调控网络;耦合反馈环；单参数

1引言

基因调控网络是由很多相互关联的组件构成的,某些有特定功能的子网称作网络单元,这些网络单元作为整体又可以相互关联。在这里,反馈环路扮演者很重要的角色。很多情况下,我们如果在已有基因调控网络的基础上添加反馈环路可以出现多样的动力学行为。但是,即使是拓扑等价的调控网络在添加拓扑等价的前反馈和后反馈后还是有很大的区别,甚至会出现相差迥异的动力学行为。

2模型的建立

这里,用小写字母“x、y、z、s”分别代表基因,用大写字母“X、Y、Z、S”分别表示对应基因产生的蛋白质。不妨考虑在含有(X,Y,Z)3个相互抑制的因子组成的负反馈环路的基础上耦合1个含有(X,Y,Z,S)4个因子组成的负反馈环路,在原有负反馈环路的基础上再耦合一个负反馈,形成如下模型(图1)。

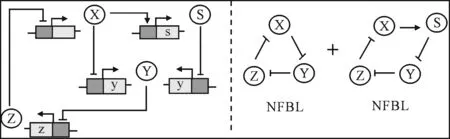
图1　模型示意

(1)

如果蛋白质X促进基因z的表达同时蛋白质Y抑制基因z的表达,那么,调控系数记作：

(2)

当蛋白质X和Y共同抑制基因z表达的时候,记调控系数为：

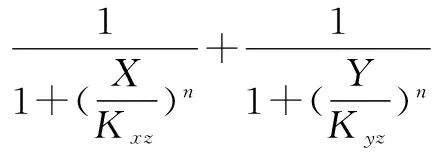
(3)

基于以上模型的假设,假如不考虑其他因素,那么它们的时间演化可由下列微分方程来确定,即：

(4)

方程中的参数取值见表1。

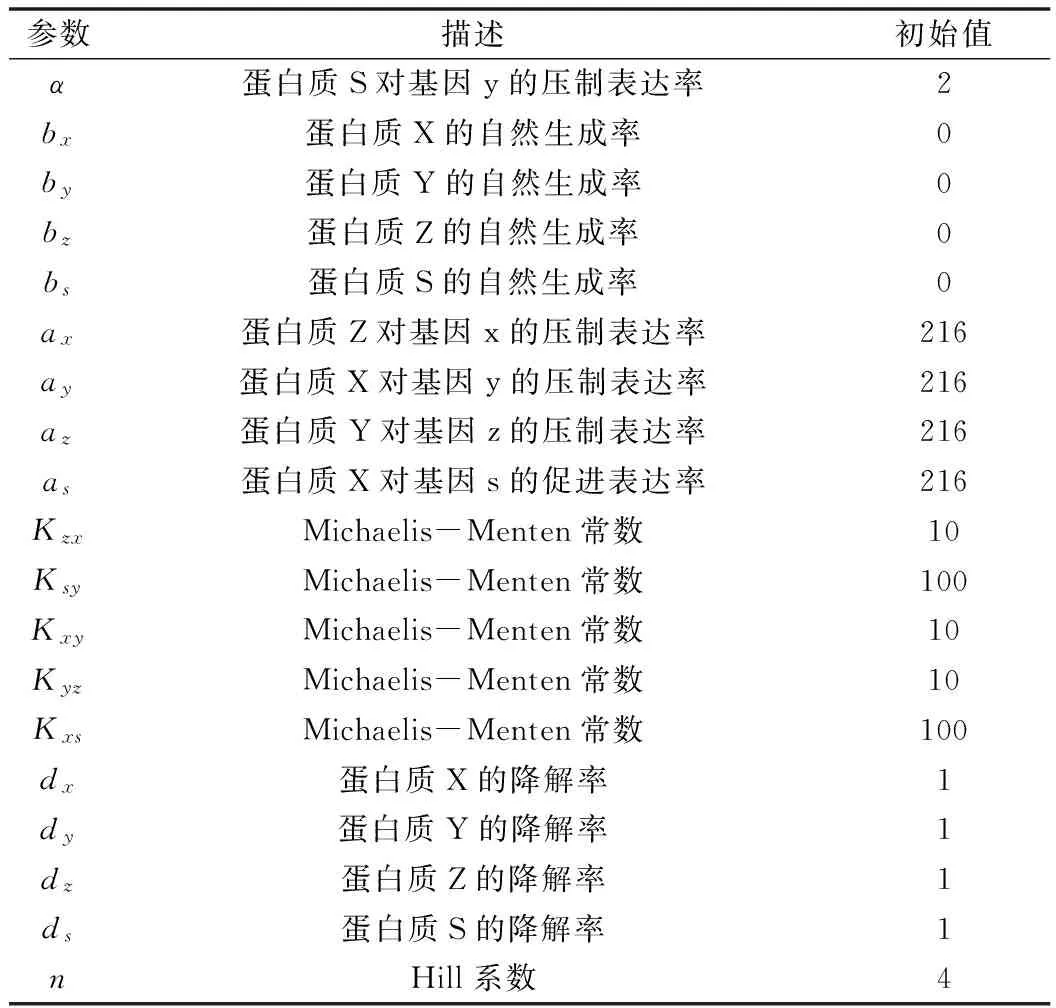
表1　随着时间演化微分方程参数取值

3单参数分析

借助XPPAUTO通过数值模拟,在生物网络的背景下,把参数α作为分岔参数。这里,考虑参数的取值区间是[0,200]。奇怪的是,当两个负反馈耦合的时候,并不是振荡减弱或者消失,相反地,还有可能随着调控参数的增加,出现更复杂的振荡,甚至还出现振荡和稳定共存的情况。

借助XPPAUTO数据分析,发现考虑的参数α∈

[0,200],被分成了5个小区间(I-V),第5个区间的参数取值范围是[21.32,200],为了更清楚的研究动力系统的解的动态,可以将参数α的取值选为[0,30],形成图2的分岔图。其中,区域I(α∈[0,14.91])和区域V(α∈[21.32,30])表示微分方程有不稳定的平衡解(图2 中黑色虚线部分)和稳定的周期解(图2 中蓝色实线部分)共存的情形,上方的蓝色线表示振动的最高位置,下方的蓝色线表示振动的最低位置。其中,点α=14.91和点α=21.32是分支点。

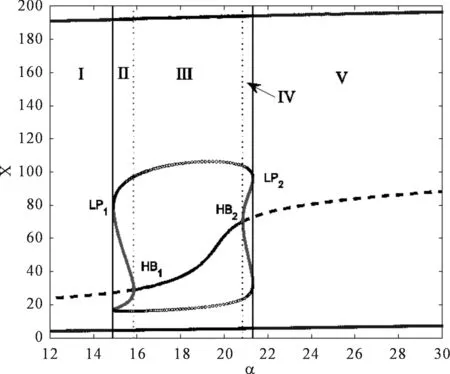
图2　α与X的分岔

在区域Ⅱ(α∈[14.91,15.85])和区域Ⅳ(α∈[20.85,21.32])系统出现丰富的动力学行为:①不稳定的平衡解(图2中黑色虚线线部分);②一个小振幅的稳定周期解(图2中红色部分),如果在这两个区域中做纵坐标轴的平行线,与红色的线部分出现两个交点,上方的交点表示振动的最高位置,下方的交点表示振动的最低位置;③一个中等振幅的不稳定的周期解(图2中黑色圆圈组成的线);④一个大振幅的稳定的周期解(图2中黑色实线部分),上方的黑色线表示振动的最高位置，下方的黑色线表示振动的最低位置。这就是说,如果参数α∈[14.91,15.85]或者α∈[20.85,21.32],系统会出现两个稳定的周期解共存的情况,点α=15.85和点α=20.85是Hopf分支点。当参数α∈[15.85,20.85]变化时,系统出现丰富的动力学行为:①稳定的平衡解(图2中黑色实线部分);②不稳定的周期解(图2中黑色圆圈组成的线);③一个大振幅的稳定的周期解(图2中黑色实线部分)。

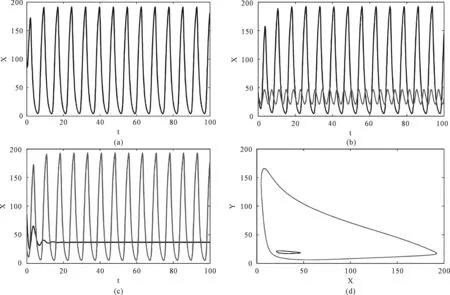
图3　X关于t的分岔以及X与Y的相

通过以上分析知道,随着参数α的变化,系统平衡点的个数也在发生变化,尤其是当α∈[15.85,20.85]时,系统会有两个稳定的周期解出现。但是,由微分方程解的存在定理可知:微分方程的解依赖于初始值,具体属于哪个稳定的周期解还要看具体初值属于哪类解的吸引域。

借助Matlab软件画出参数α不同初始值时系统解的状态,见图3。

其他参数不变,图3(a)中,取参数α=14和初始值取X(0)=95,Y(0)=96,Z(0)=15,S(0)=97时,系统有稳定的周期解; 图3(b)中，取参数α=15和初始值取X(0)=42,Y(0)=91,Z(0)=79,S(0)=95时,系统有大振幅的周期解;如果初始值取X(0)=25,Y(0)=16,Z(0)=11,S(0)=49时，系统有小振幅的周期解; 图3(c)中,取参数α=18和初始值取X(0)=85,Y(0)=34,Z(0)=58,S(0)=22时,系统有稳定的平衡解; 取参数α=18和初始值取X(0)=25,Y(0)=34,Z(0)=58,S(0)=22时,系统有周期解。图3(d)中，取与图3(b)中有相同参数值和初始值的相图，即两个极限环。这与上面分析的α取值的五个区域分别对应的稳定解的个数是吻合的。

参考文献：

[1]王高雄,周之铭,朱思铭，等,常微分方程[M].3版.北京：高等教育出版社,北京,2006.

[2]陈爱敏,生化网络中噪声信号的传播机制研究[D].广州:中山大学,2009.

[3]傅祖芸.信息论：基础理论与应用[M].北京：电子工业出版社,2006.

[4]周天寿,系统生物学[M].北京：科学出版社,2009.

[5]TOSTEUIN F, WOLDE P. Mutual Information in Time-varying Biochemical Systems[J].Physical Review,2010,81:061917.

收稿日期：2016-04-10

作者简介：刘彩霞(1988—),女,助理教师，主要从事应用数学的教学与研究工作。 毕小山(1966—),男,副教授,主要从事应用数学的教学与科研工作。

中图分类号：Q-332

文献标识码：A

文章编号：1674-9944(2016)10-0236-03