认识三角形(第1课时)教学设计
2016-07-18刘雪
刘雪
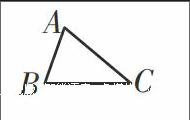
一、学情分析
学生在第二章对两直线平行的条件及平行线的性质进行了探索,具备了利用平行线的性质得出三角形内角和结论的基本知识和基本技能。小学学习三角形内角和的结论时是通过撕、拼的方法得到的,具备了直观操作的经验,同时以前的数学学习,学生经历了合作学习的过程,具备了合作学习的经验和能力。
二、教学目标
(1)知识与技能:认识三角形的有关概念及要素,掌握三角形内角和等于180°和直角三角形两锐角互余,会对三角形按角分类。
(2)过程与方法:通过观察、操作、想象、推理的活动过程,发展空间观念,推理能力和有条理地表达能力。
(3)情感与态度:在探究学习中体会数学的现实意义,培养学生学习数学的信心,体验解决问题方法的多样性。
三、教学重点、难点
重点:三角形的相关概念,三角形内角和等于180°,直角三角形两锐角互余。
难点:三角形内角和等于180°的探究与合情推理。
四、教学方法
引导发现法,合作探究法。
五、教学准备
三角板,多媒体。
六、教学过程
第一环节:活动引入
活动内容:让学生画出一个三角形,用三根笔摆出一个三角形。
活动目的:使学生能从活动中回顾旧知,引起学习兴趣,为后续探究做好铺垫。
第二环节:概念讲解
参照学生所画图形,提出问题——这些三角形有什么共同的特点?
归纳:
1.三角形定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫作三角形。符号表示:△,如图△ABC。
2.三个基本要素:边,角,顶点。
活动目的:通过画图、摆图,引导学生归纳三角形的概念、基本要素,培养学生观察分析及归纳总结的能力。
3.练习题:
如图,图中共有几个三角形?其中以AB为边的三角形有几个?AB是哪几个三角形的公共边?∠C是哪几个三角形的公共角?
习题目的:加深对三角形概念的理解。
第三环节:操作探究
1.4人小组合作,利用课前准备的任意三角形纸片,撕、拼等方法验证三角形内角和为180°,然后各小组选派代表展示设计的方案并合情说理。
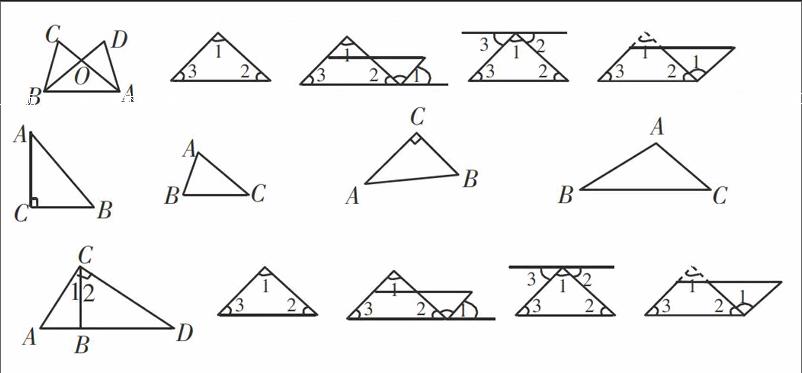
2.学生设计验证方法图:
3.第三个图拼出的学生不多,第四个图有困难,需老师启发引导:
生答:三个角拼出了平角。(第二个图学生容易拼出,并说理清楚)
师问:撕两个角还可怎样拼?(一角的两侧)
师说:第二章,我们也学习了180°,在什么情况下会有180°的角出现呢?
生答:两直线平行,同旁内角互补。
师问:那能不能只撕一个角去拼呢?
启发:利用PPT动画效果,让学生感受角的位置发生变化,但角的大小没变。
学生小组讨论动手撕拼,老师指导,学生合情说理。
归纳:三角形三个内角的和等于180°。
活动目的:学生在探究过程中,教师到各小组指导,参与他们的讨论,有针对性地启发和指导,从而突出和解决了本节课的重、难点。
4.练习题:在△ABC中,
(1)∠C=70°,∠A=50°,则∠B=______。
(2)∠B=100°,∠A=∠C,则∠C=______。
(3)2∠A=∠B+∠C,则∠A=______。
习题目的:运用并掌握三角形三个内角和等于180°,掌握用方程思想求三角形的角度问题。
2.一个三角形最多有几个直角?几个钝角?几个锐角?
第四环节:三角形分类
1.观察下图三角形三个内角的特点,可以将三角形按角分类:
分类:锐角三角形,直角三角形,钝角三角形。
2.直角三角形的符号、斜边、直角边,有一个内角为90°的三角形,叫作直角三角形(数学符号:Rt△)。
夹直角的两边称为直角边,
直角的对边称为斜边。
3.师问:直角三角形有许多性质,你能发现它的两个锐角之间有什么关系吗?
发现:直角三角形两个锐角互余。
活动目的:使学生借助图形,根据三角形内角的大小,把三角形按角分类。通过对三角形分类的学习,使学生了解分类讨论的思想。
4.练习题:
(1)直角三角形一个锐角为70°,另一个锐角( )度。
(2)一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和60° (2)40°和70° (3)50°和20°
(3)已知∠ACB=90°,CD┴AB于D,
(1)图中有几个Rt△?分别是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?
习题目的:练习是由易到难,由简到繁设计的,便于学生循序渐进地掌握知识。在练习的过程中使不同的学生得到不同的发展,特别是“学习有困难”的学生也能够积极参与。
第五环节:课堂小结
1.这节课你学到了哪些知识?
2.你学会了哪些解决问题的方法?
3.你还有哪些问题?
活动目的:鼓励学生结合本节课的学习谈自己的收获与感想,并敢于说出自己的困惑。
第六环节:布置作业
习题4.11,2(直接填写在教材上),3,5。
七、板书设计
认识三角形。
1.三角形定义。
2.三角形三个内角的和等于180°。
3.三角形按角分类。
锐角三角形,直角三角形,钝角三角形。
4.直角三角形两个锐角互余。
八、教学反思
1.学生在教师创设的情境下,动手操作、思考、表达三角形内角和等于180°,发展了学生的实践能力。
2.通过让学生剪、拼及合情说理,使学生的感性认识和理性认识都得到提高。
3.每个环节都配有练习题,便于学生及时加深对知识的理解。
4.若能更好地把握时间和节奏,效果会更好。在备课时,更应思考学生怎么学,教师如何促进学生学。
(作者单位:西北大学附属中学)
