对非合作目标逼近的非奇异终端滑模控制

刘海龙，　史小平

(哈尔滨工业大学 控制与仿真中心，黑龙江 哈尔滨 150001)



对非合作目标逼近的非奇异终端滑模控制

刘海龙，史小平

(哈尔滨工业大学 控制与仿真中心，黑龙江 哈尔滨 150001)

摘要:针对失控慢速翻滚非合作目标终端逼近过程的六自由度控制问题进行研究。首先，建立适用于任意偏心率的相对轨道和姿态动力学模型。其次，将系统的外部扰动、模型不确定性及系统非线性项统一表示为“总扰动项”，并基于扩张状态观测器的相关理论，设计用以获得“总扰动项”估计值的扩张状态观测器。在此基础上，利用非奇异终端滑模控制理论，设计仅需相对位置和姿态测量信息的非奇异终端滑模输出反馈控制器。基于Lyapunov理论证明了系统稳定性。所设计控制器具有模型独立的特点，克服了航天器动力学参数的不确定性，并且可在有限时间内跟踪期望轨迹。最后，通过数值仿真验证了控制器的正确性和有效性。

关键词:非合作目标；相对运动；输出反馈；非奇异终端滑模；扩张状态观测器

0引言

随着空间技术及应用的不断发展，对非合作目标的在轨服务技术引起了学界的广泛关注。空间非合作目标泛指一类不能提供有效合作信息的空间物体，包括故障或失效卫星、空间碎片以及对方航天器等。国内外对此投入大量经费进行研究，例如日本在1997年成功发射的无人自主交会对接试验卫星(ETS-VII项目)，美国于2007年进行的“轨道快车(orbital express, OE)”试验[1-2]，以及由DLR与轨道恢复(orbital recovery, OR)公司合作，用以研制寿命10～15年的在轨服务卫星轨道寿命延长飞行器(orbital life extension vehicle, OLEV)[3-4]。

航天器近距离运动的六自由度控制是控制领域的重要问题，由于在近距离操作中，姿态和轨道的相互耦合作用，使得空间操作的安全性受到威胁，从而加大了控制的难度。Xu在文献[5]中建立了六自由度位置姿态耦合动力学模型，针对自由旋转目标设计了全局稳定的滑模控制器，并将遗传算法应用到对控制器参数的选取中。Kristiansen[6]针对“leader-follower”飞行器的协同控制问题，分别应用积分反步法、PD+以及滑模控制方法进行控制器的设计，并通过仿真对三种控制器的控制效果进行了比较。Shan[7]在考虑周期摄动和参数不确定性的情况下，通过设计滑模控制器，使得飞行器能够以同步飞行模式对期望姿态和位置进行跟踪，并通过仿真验证了所设计控制器的有效性。Chung[8]等通过拉格朗日形式的动力学模型对飞行器的姿轨同步控制问题进行了研究，设计了全局指数稳定的分散跟踪控制律。Lv[9]等在考虑输入约束与参数不确定性的情况下，针对飞行器的编队飞行问题设计了反步控制器，利用Lyapunov稳定性理论证明了系统的稳定性。Welsh[10]对非合作目标的同步逼近问题进行了研究，设计了PID制导律以及自适应姿态控制律，通过仿真验证了控制器的有效性。Matsumoto[11]针对旋转目标的终端交会过程，提出了飞越逼近和瞬间捕获的策略，并通过仿真验证了这一方法。李九人[12]等通过设计参考轨迹及参考姿态，并利用滑模控制方法实现了对无控旋转目标的逼近。

冯勇等人在文献[13]中提出了一种新型滑模控制方法——非奇异终端滑模控制，该方法在继承终端滑模控制有限时间收敛特性的同时，解决了现有终端滑模存在的奇异性问题。扩张状态观测器作为自抗扰控制的核心技术，除能对系统的状态进行估计之外，还能对系统的非线性项及外界干扰进行有效估计[14-15]，在航天器的控制研究中得到广泛应用。袁国平[16]基于扩张状态观测器，提出了一种仅需要姿态角测量值的自适应输出反馈控制策略，仿真结果表明，在多种任务模式下，航天器均可很好地完成姿态机动任务。

本文首先建立了用以描述近距离相对运动且适用于任意偏心率的相对轨道和姿态动力学模型。其次为了获取系统的非线性耦合项及外界干扰信息，设计了扩张状态观测器。在此基础上，基于非奇异终端滑模控制理论设计了输出反馈控制器。

1模型建立

1.1相对轨道动力学

将对旋转非合作目标逼近所涉及到的两个卫星分别定义为目标星和追踪星，且假设目标星自由运行于开普勒轨道，追踪星具有轨道和姿态机动能力。首先对目标星轨道坐标系进行定义，如图1所示，目标星轨道坐标系Oxyz，原点O位于目标星质心，x轴沿轨道切线方向，z轴沿地球矢径方向且指向地心，y轴与x轴和z轴构成右手坐标系。 下文将通过二体运动方程推导出相对轨道动力学方程。

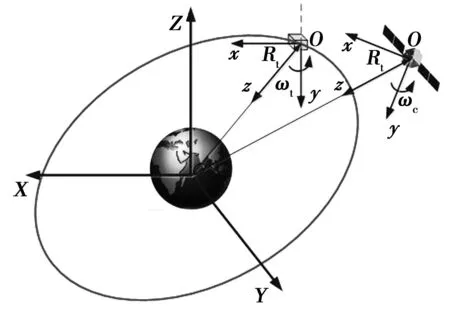
图1　坐标系定义Fig.1　The definition of coordinate system

由二体运动方程可知[17]

(1)

式中：rc和rt分别为追踪星和目标星质心的地心矢量；μ为地球引力常数；fdc、fdt分别为追踪星与目标星上的摄动力；Fc为作用在追踪星上的控制力；mc、mt分别为追踪星和目标星的质量。

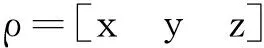
(2)

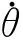
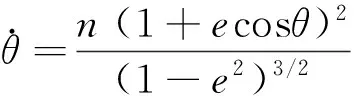
(3)

(4)

其中，n为目标器平均角速度，e为轨道偏心率。根据式(2)可得如下形式的非线性相对轨道动力学方程

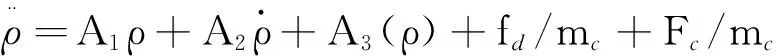
(5)

其中

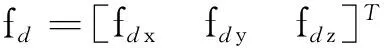
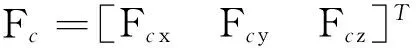
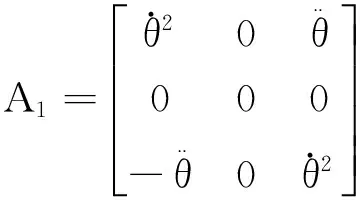
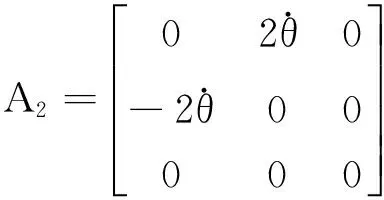
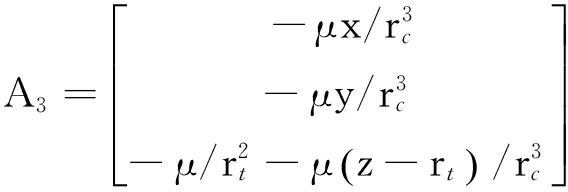
1.2相对姿态动力学方程

将分别建立追踪星和目标星的姿态动力学方程，进而推导出两卫星之间的相对姿态动力学方程。假设两卫星均为刚体，则追踪星和目标星的姿态动力学方程可分别表示为

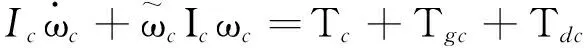
(6)

(7)

其中，Ic和It为两卫星的转动惯量；ωc和ωt为两卫星本体坐标系相对于惯性坐标系且表示在本体坐标系下的姿态角速度；Tc为追踪星姿态控制力矩；Tgc，Tgt为重力梯度力矩；Tdc，Tdt为干扰力矩。

注1对Euclidean空间中任意n维向量x∈Rn，其范数均指2范数。

式(6)、式(7)中的重力梯度力矩可由下式给出：

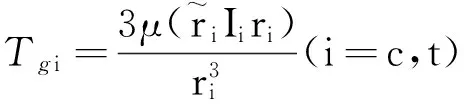
(8)

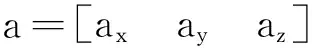
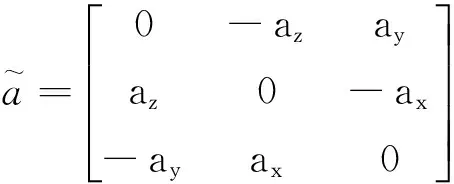
(9)

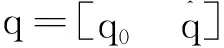
(10)

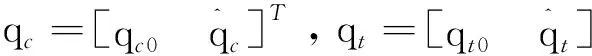
Act=Aci(Ati)T=A(qc)A(qt)。

(11)

设qr为追踪星相对于目标星的误差四元数，则有

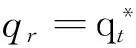
(12)

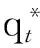
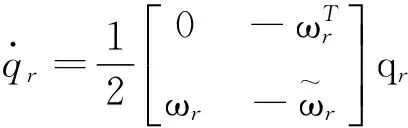
(13)

对式(13)求导，可以得到

(14)

设ωr为追踪星相对于目标星的姿态角速度在追踪星本体坐标系下的表示，则有

ωr=ωc-Actωt。

(15)

对式(15)求导有

(16)

式中

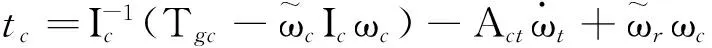
(17)

将式(16)代入式(14)中可得

(18)

由此便可得到非线性相对姿态动力学方程：

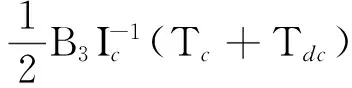
(19)

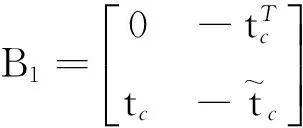
1.3六自由度耦合动力学模型

(20)

式中

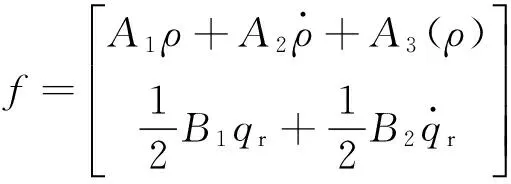
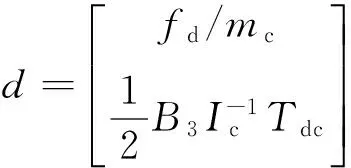
2扩张状态观测器设计

在实际航天器任务中，由于研制过程中经济性和使用性的限制，有时将选择不安装姿态角速度敏感器，或者由于敏感器故障使得姿态角速度信息无法输出，上述两种情况都将无法实际获得系统的全部状态，从而使状态反馈的物理实现难以进行。另外，考虑到存在外部干扰和转动惯量不确定性，以及系统中存在着未建模动态，故在系统(20)中，f这样的非线性耦合项往往很难精确获得。为此，本文在只有相对位置和姿态测量信息的条件下，通过ESO估计出系统的其他状态和未知的非线性耦合项。

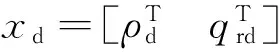
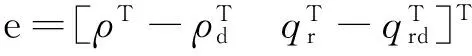
(21)

对式(21)求导，可得误差矢量的一次导数为

(22)

则系统的误差状态方程为

(23)

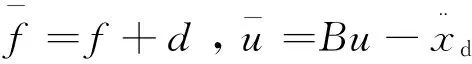
(24)

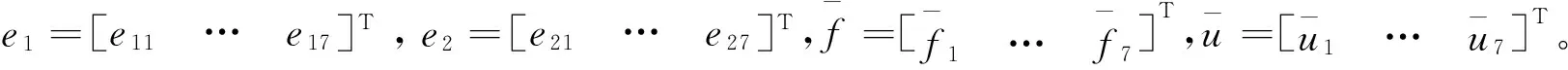
将误差状态方程(24)写成分量形式为

(25)

式中，i=1,2,…,7。

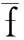
(26)

按式(26)对这个被扩张的系统建立扩张状态观测器

(27)

式中，fal(e0i,αi,δi)为在原点附近有线性段的非线性函数

(28)

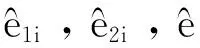
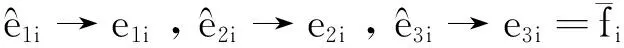
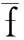
3非奇异终端滑模控制器设计

非奇异终端滑模(nonsingularterminalslidingmode,NTSM)控制方法是近年来出现的一种新型滑模控制方法[13],它通过有目的地改变切换函数，直接从滑模设计方面解决了现有终端滑模控制存在的奇异性问题，实现了系统的全局非奇异控制；同时它又继承了终端滑模的有限时间收敛特性，与传统的线性滑模控制相比，可令控制系统有限时间内收敛到期望轨迹，且具有较高的稳态精度，特别适用于高速、高精度控制。本文将基于NTSM控制方法，结合ESO对“总扰动项”的估计结果，对系统(20)进行控制器设计，控制目标为在有限时间内实现对期望相对位置和相对姿态的精确跟踪。

针对姿轨耦合动力学系统(20)，首先给出下述合理假设

假设1：两航天器的三轴相对位置、相对姿态角信息可测量、光滑且有界。

假设2：系统所受的外界干扰有界，即

式中，dm为已知函数，表示外部扰动上界。

假设3：主动航天器的未知质量特性满足

mmin≤m≤mmax,

Jijmin≤Jij≤Jijmax,i,j=1,2,3。

其中，mmin和mmax分别为航天器质量m的最小值和最大值；Jijmin和Jijmax分别为对应的转动惯量矩阵元素Jij的最小值和最大值。

目前，常用的滑模控制律设计方法是滑模等效控制方法，控制律通常包含等效控制项和切换控制项两部分[17]。

(29)

式中，F为已知函数，用以表示“总扰动项”的估计误差上界。

首先设计切换函数如下式所示

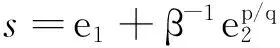
(30)

定理1对于跟踪误差系统(24)，选取非奇异终端滑模面(30)，如果采取如下控制策略，则跟踪误差系统将在有限时间内收敛到零。

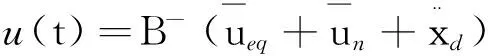
(31)

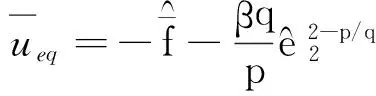
(32)

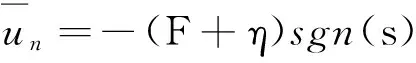
(33)

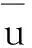
η=diag(η1,…,η7)，ηi>0，i=1,2,…,7

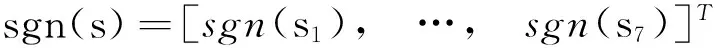
B-为B的广义逆矩阵，根据广义逆矩阵的基本理论可知B-的计算表达式为

B-=(BTB)-1BT。

(34)

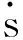
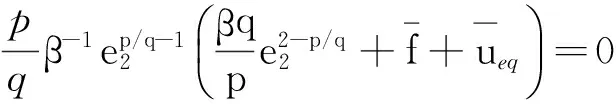
(35)

故可以得到等效控制如式(32)所示。由式(32)可以看到，由于1

0，与终端滑模的等效控制项相比，可以从理论上保证非奇异终端滑模控制器不会存在控制奇异区域。本文选取非线性控制项如式(33)所示。

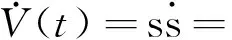
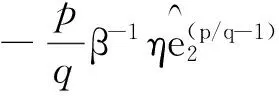
(36)

因此，在控制律(31)作用下，含有系统不确定性的跟踪误差系统(24)将在有限时间内收敛到零，即追踪星将在有限时间内到达期望的相对位置与相对姿态，且对系统不确定性具有强鲁棒性。

由文献[13]可知，若滑动模态s在tr时刻到达滑模面s=0，则e1和e2将在有限时间内收敛至零，收敛时间为

(37)

证毕。

4仿真分析

设目标星的轨道六要素为a=6 900 000m，e=0.001，i=100°，Ω=70°，w=30°，f=125°考虑地球非球星摄动和大气阻力的影响，对非合作目标的终端逼近过程进行了高精度数值仿真。假设在距离目标星约10 m处追踪星开始进行对目标星地终端逼近，在距离目标星轨道面法线方向2 m处进行悬停，故可设初始相对位置和相对速度矢量为

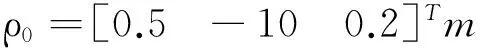
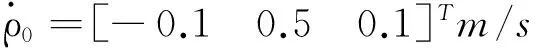
设期望的相对位置和相对速度矢量为：

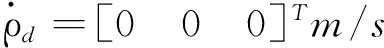
追踪星的质量为45 kg,目标星质量为6 kg，由于逼近过程较短，本文在仿真过程中暂不考虑质量变化及转动惯量的不确定性，将其视为常值，并设转动惯量的值为

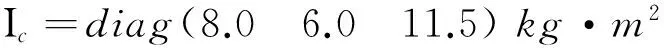
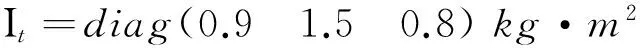
初始时刻追踪星和目标星的姿态四元数分别为

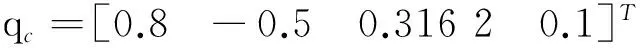
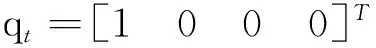
追踪星和目标星的初始姿态角速度分别为

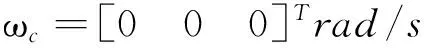
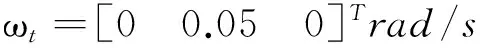
βi=0.05，i=(1,2,…,7)，

p=5，q=3。

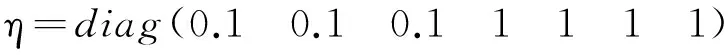
假设未建模的相对摄动力和摄动力矩表达式为

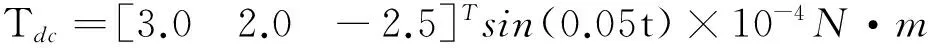
如图2和图3所示分别为目标星轨道坐标系下的相对位置曲线和相对速度曲线，在非奇异终端滑模控制器作用下，追踪星沿参考轨迹约在50s内完成终端逼近过程，到达指定的悬停位置。

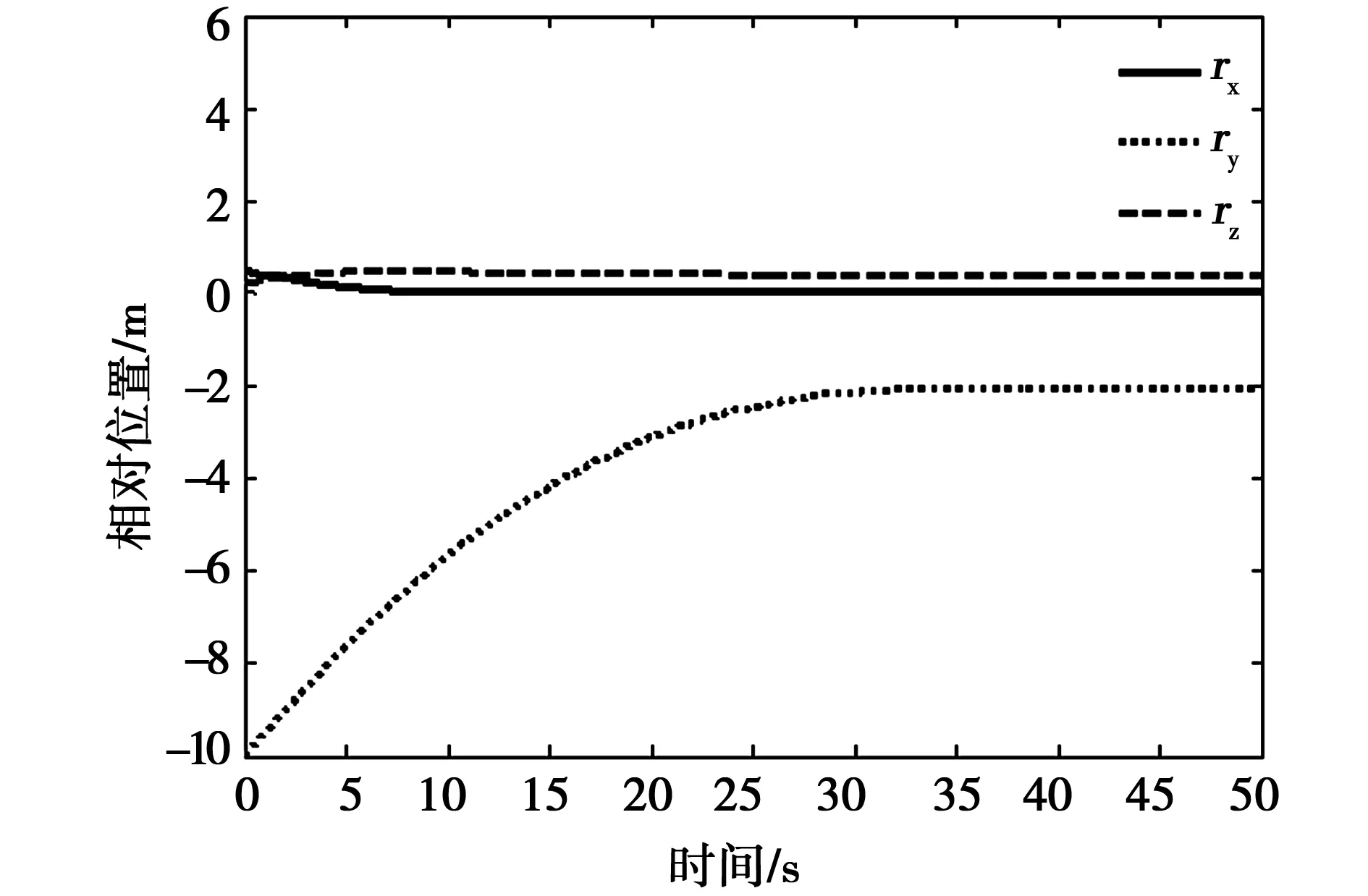
图2　相对位置曲线Fig.2　Relative position versus time

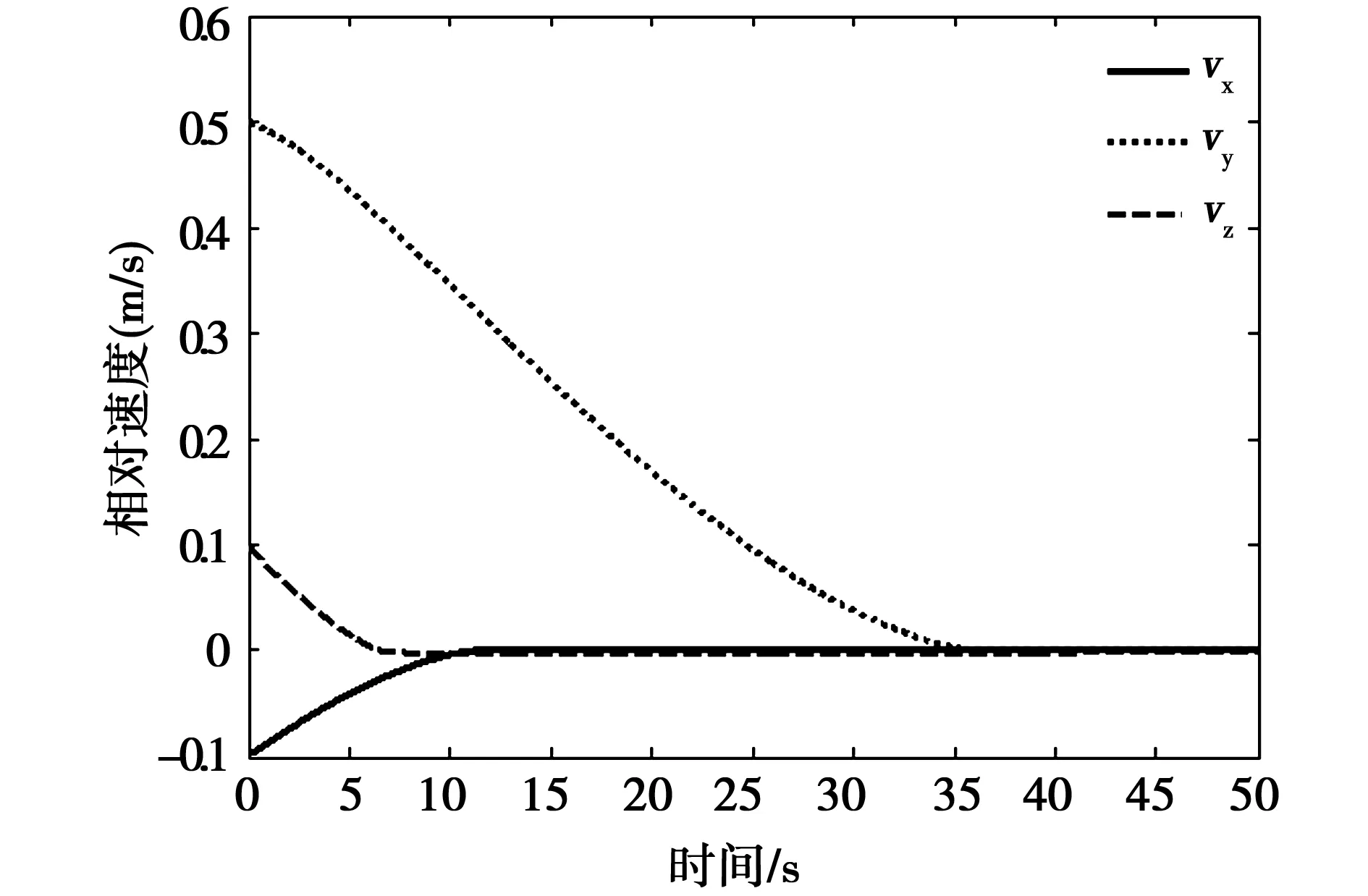
图3　目标星轨道坐标系下相对速度曲线Fig.3　Relative velocity versus time

如图4所示为追踪星姿态与目标星姿态之间的误差四元数曲线，根据仿真计算结果，追踪星在15 s内完成了对目标星初始相对姿态的捕获，而在接下来的逼近过程中对目标星姿态进行跟踪。图5和图6为追踪星在终端逼近过程中的控制力与控制力矩变化情况。由于初始阶段追踪星要尽快追踪参考轨迹，所以控制力在初期较大，但随着相对距离的减小，控制力呈减小趋势。由控制力矩的变化过程可知，由于初期追踪星要尽快进行姿态捕获以实现对目标器的姿态跟踪，所以控制力矩较大。后续只需要较小的力矩便可实现对期望姿态的追踪。

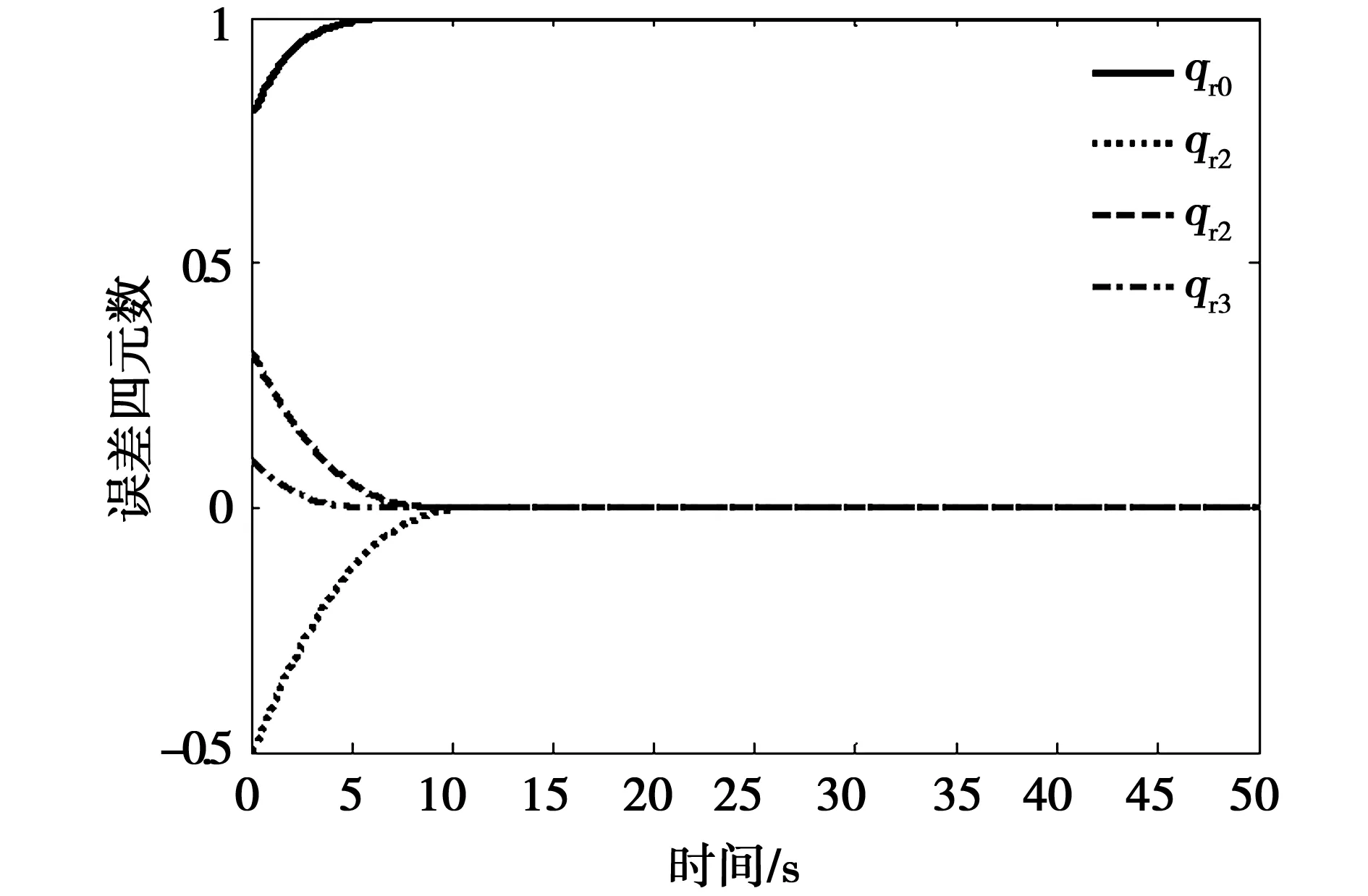
图4　误差四元数曲线Fig.4　Error quaternion versus time

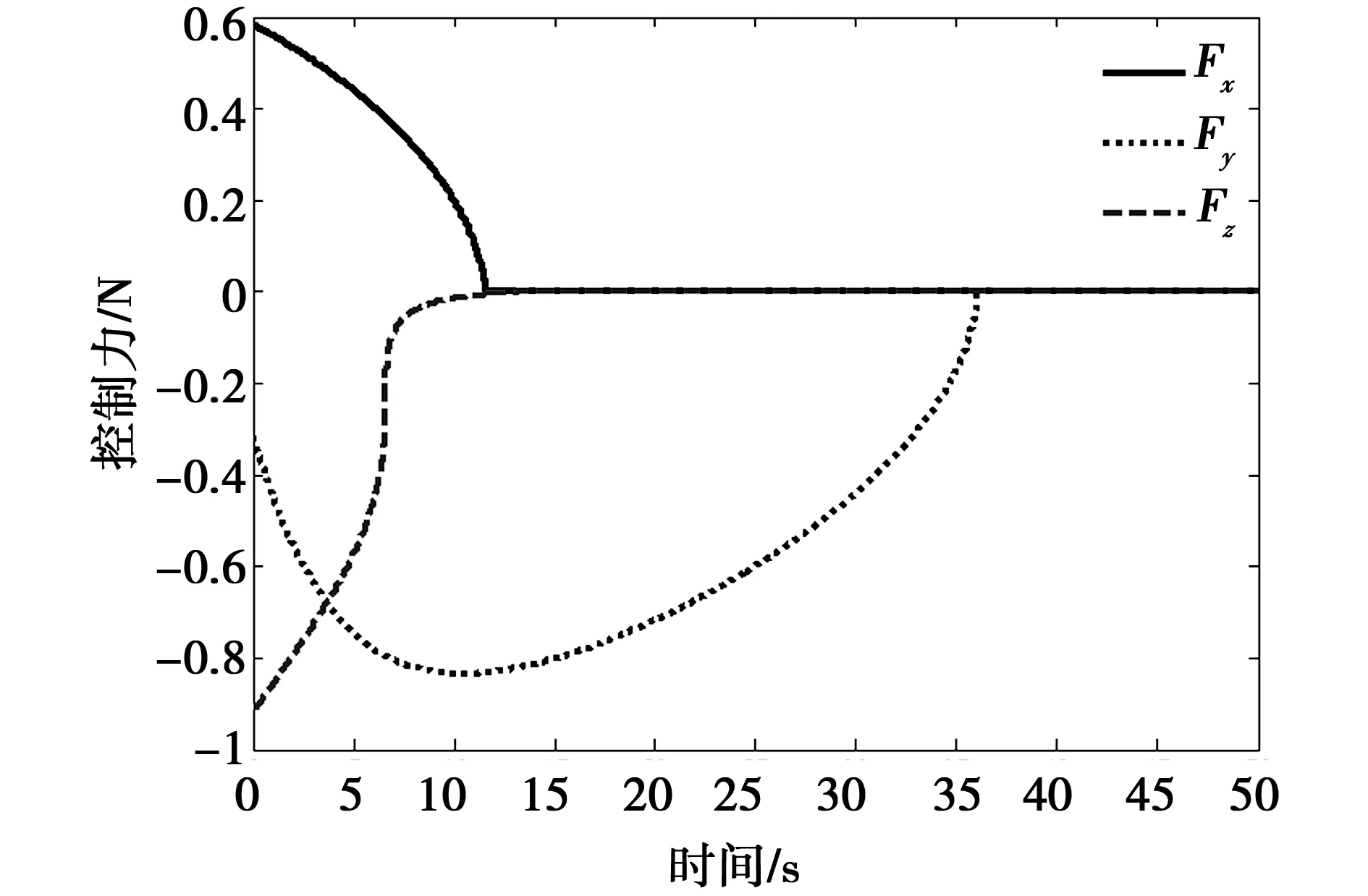
图5　控制力变化曲线Fig.5　Control force versus time

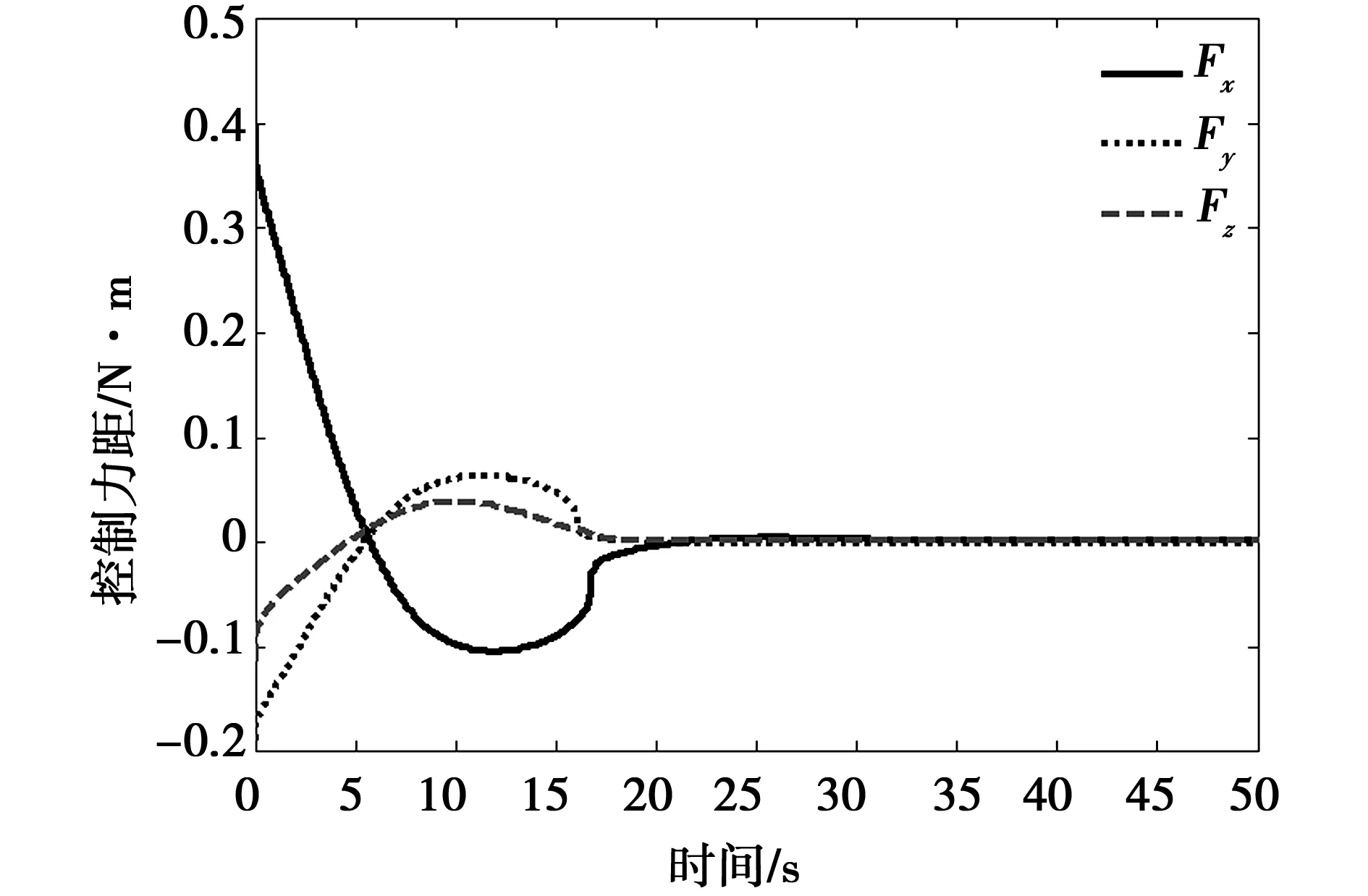
图6　控制力矩变化曲线Fig.6　Control torque versus time

如图7所示为相对位置、相对速度及相对姿态跟踪误差估计情况，由此可以看出扩张状态观测器可以对相对位置、相对速度及相对姿态与控制指令之间的偏差可以进行很好的估计，此跟踪误差在20 s内趋于零，这也反映了在控制器的作用下，相对位置、相对速度及相对姿态精确地跟踪了参考指令。

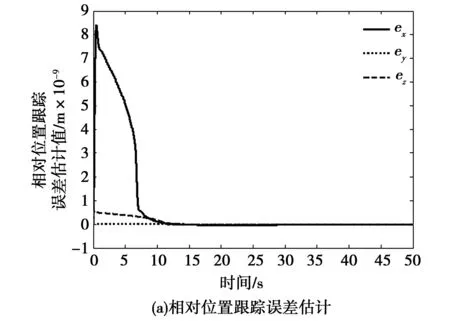
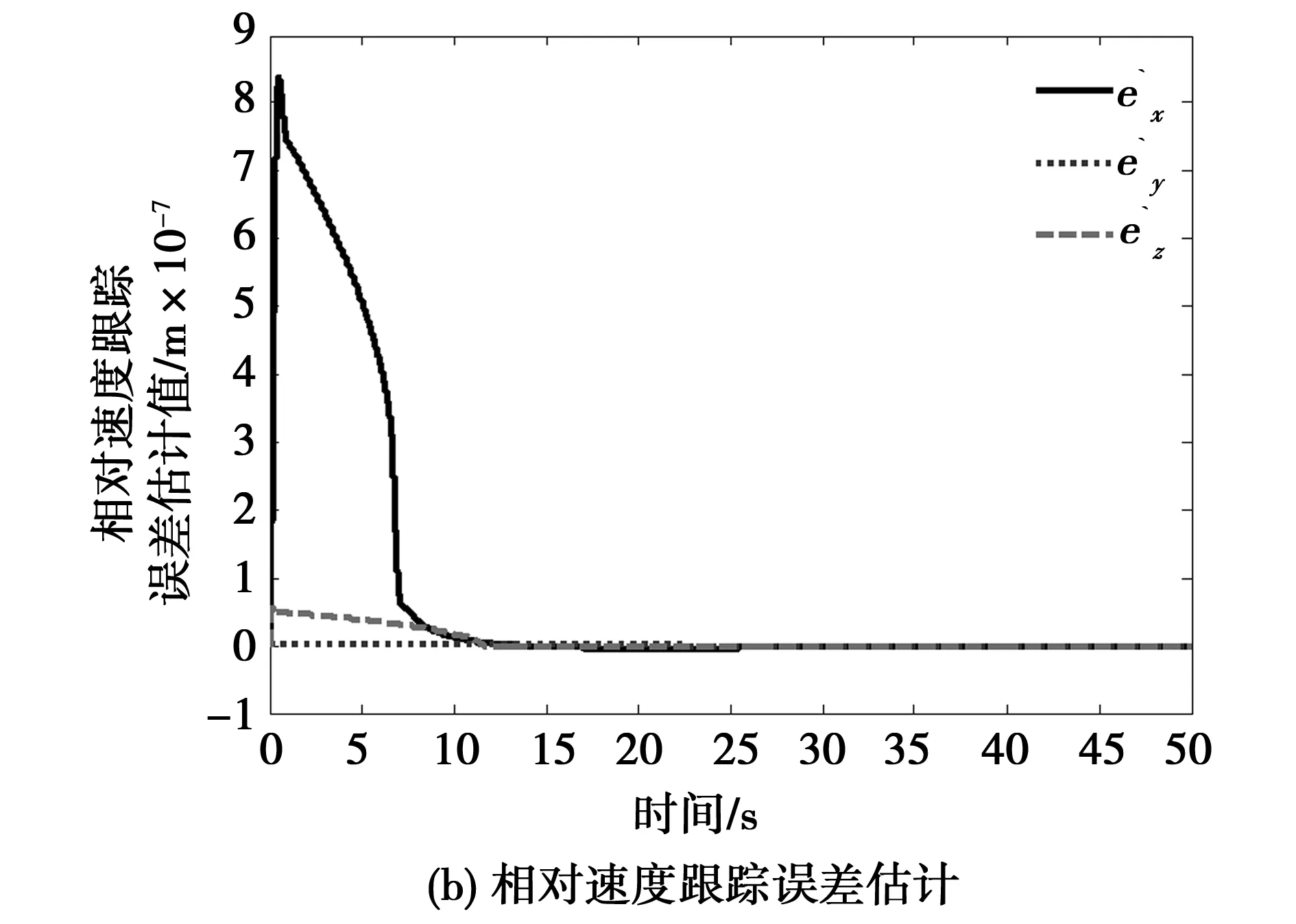
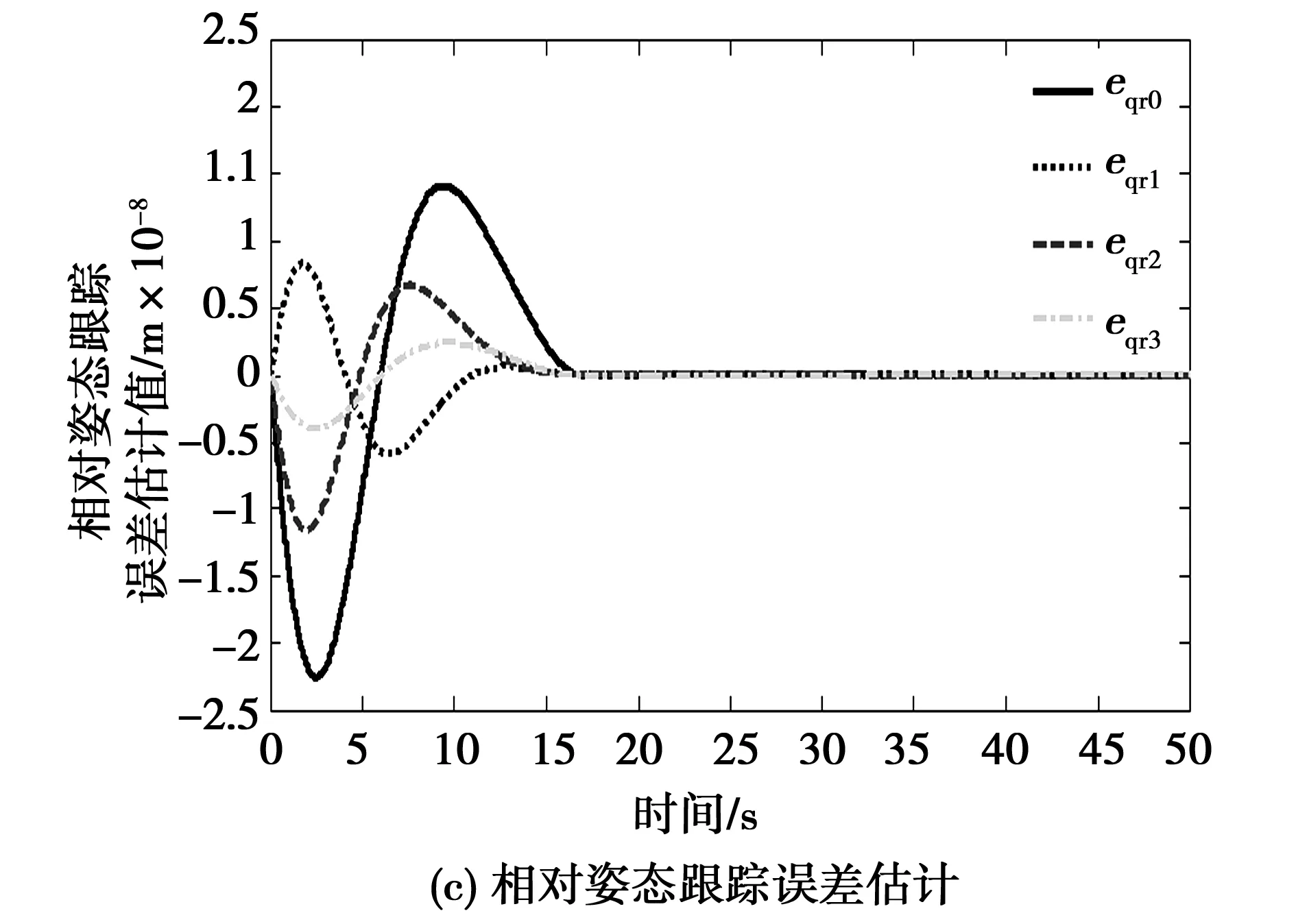
图7　相对位置、相对速度及相对姿态跟踪误差估计Fig.7　　　　Estimation of relative position,relative velocity,　　　relative attitude tracking error

5结论

1)建立了适用于任意偏心率的六自由度轨道姿态耦合动力学模型，对非合作目标终端逼近过程进行了描述；

2)设计了扩张状态观测器，从而对系统的“总扰动项”(包括系统状态、非线性耦合项以及外界干扰)进行了估计，实现了在仅具有相对距离和相对姿态角测量值情况下的系统状态估计，以及为后续设计非奇异终端滑模输出反馈控制器打下基础；

3)设计了基于扩张状态观测器的非奇异终端滑模输出反馈控制器，从而实现了在仅有相对距离和相对姿态角情况下的姿轨一体化控制。利用Lyapunov直接法证明了系统的稳定性。仿真结果验证了所设计控制器的有效性。

参 考 文 献:

[1]PINSON R M, HOWARD R T, HEATON A F. Orbital express advanced video guidance sensor: ground testing, flight results and comparisons[C]//Proceedings of AIAA Guidance, Navigation and Control Conference, August 18-21, 2008, Honolulu, United States. Reston:AIAA,2008: 2008-7318.

[2]HEATON A F, HOWARD, R T, PINSON R M. Orbital express AVGS validation and calibration for automated rendezvous[C]//Proceedings of AIAA/AAS Astrodynamics Specialist Conference, August 18-21, 2008, Honolulu, United States. Reston:AIAA,2008: 2008-6937.

[3]DELCURA J M, SAAVEDRA G, SANCHEZ-MAESTRO R, et al. Conexpress orbital life extension vehicle (CX-OLEV) GNC[C]//Proceedings of AIAA 57th International Astronautical Congress, October 2-6, 2006, Valencia, Spain. Reston:AIAA,2006: 4720-4733.

[4]TARABINI L, GIL J, GANDIA F. Ground guided CX-OLEV rendezvous with uncooperative geostationary satellite[J]. Acta Astronautica, 2007, 6(12): 1014-1018.

[5]XU Y J, TATSCH A, FITZ-COY N G. Chattering free sliding mode control for a 6-DOF formation flying mission[C]//Proceedings of AIAA Guidance, Navigation and Control Conference, August 15-18, 2005, San Francisco, United States. Reston:AIAA,2006: 6210-6219.

[6]KRISTIANSEN R, NICKLASSON P J, GRAVDAHL J T. Spacecraft coordination control in 6 DOF: integrator backstepping vs passivity-based control[J]. Automatica, 2008, 44(11): 2896-2901.

[7]SHAN J. Six-degree-of-freedom synchronised adaptive learning control for spacecraft formation flying[J]. IET Control Theory and Applications, 2008, 2(10): 930-949.

[8]CHUNG S J, AHSUN U, SLOTINE J-J E. Application of synchronization to formation flying spacecraft: lagrangian approach[J]. Journal of Guidance, Control and Dynamics, 2009, 32(2): 512-526.

[9]LV Yueyong, HU Qinglei, MA Guangfu, et al. 6-DOF Synchronized control for spacecraft formation flying with input constraint and parameter uncertainties[J]. ISA Transactions, 2011, 50(4): 573-580.

[10]WELSH S J, SUBBARAO K. Adaptive synchronization and control of free flying robots for capture of dynamic free-floating spacecrafts[C] //Proceedings of AIAA/AAS Astrodynamics Specialist Conference, August 16-19, 2004, Providence, United States. Reston:AIAA,2004: 1193-1214.

[11]MATSUMOTO S, DUBOWSKY S, JACOBSEN S, et al. Fly-by approach and Guidance for uncontrolled rotating satellite capture[C]//Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit, August 11-14, 2003, Austin Texas. Reston:AIAA,2004: 2003-5745.

[12]李九人, 李海阳, 唐国金. 对无控旋转目标逼近的自适应滑模控制[J]. 宇航学报, 2011, 32(4): 815-822.

LI Jiuren, LI Haiyang, TANG Guojin. Adaptive sliding mode control for approach to uncontrolled rotating satellite[J]. Journal of Astronautics, 2011, 32(4): 815-822.

[13]冯勇, 鲍晟, 余星火. 非奇异终端滑模控制系统的设计方法[J]. 控制与决策, 2002, 17(2): 194-198.

FENG Yong, BAO Sheng, YU Xinghuo. Design method of non-singular terminal sliding mode control systems[J]. Control and Decision, 2002, 17(2): 194-198.

[14]韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策, 1995, 10(1)：85-88.

HAN Jingqing. A class of uncertain objects of the extended state observer[J]. Control and Decision, 1995, 10(1): 85-88.

[15]黄一, 韩京清. 非线性连续二阶扩张状态观测器的分析与设计[J]. 科学通报, 2000, 45(13): 1373-1379.

HUANG Yi, HAN Jingqing. Analysis of nonlinear continuous second order extended state observer and the design[J]. Chinese Science Bulletin, 2000, 45(13)： 1373-1379.

[16]袁国平, 史小平, 李隆. 基于扩张状态观测器的航天器自适应姿态控制[J]. 中国空间科学与技术, 2011, 31(5)：9-17

YUAN Guoping, SHI Xiaoping, LI Long. The adaptive attitude control for spacecraft based on the extended state observer[J].Chinese Space Science and Technology, 2011, 31(5)：9-17.

[17]章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社，1998:1-7.

ZHANG Renwei. Dynamics and control for satellite attitude and orbit [M]. Beijing: Beihang University Press, 1998:1-7.

(编辑：刘素菊)

Nonsingular terminal sliding mode control for approach to non-cooperative target

LIU Hai-long，SHI Xiao-ping

(Control and Simulation Center, Harbin Institute of Technology, Harbin 150001, China)

Abstract:The problem of final approach to a non-cooperative tumbling target was researched. The relative orbit and attitude dynamics model with arbitrary eccentrics was established. Then, the system’s external disturbance, model uncertainty and the system nonlinear term were expressed as total disturbance. Based on the theory of extended state observer (ESO), ESO was designed to estimate the total disturbance. Furthermore, by applying the nonsingular terminal sliding mode control method, the nonsingular terminal sliding mode control law was designed, which just needs the relative position and attitude measurement information. The stability of the control law was demonstrated via a Lyapunov analysis. The designed controller is model independent, which overcomes the problem of unknown dynamics parameters and can track the desired trajectory in finite time. The numerical simulation shows the effectiveness of the controller.

Keywords:non-cooperative target; relative motion; output feedback; nonsingular terminal sliding mode; extended state observer

收稿日期:2015-09-12

基金项目：国家自然科学基金(61203191)；航空科学基金(20140177006)

作者简介：刘海龙(1987—)，男，博士研究生，研究方向为飞行器控制、非线性控制等； 史小平(1965—)，男，博士，教授，研究方向为系统仿真、飞行器控制等。

通讯作者:刘海龙

DOI:10.15938/j.emc.2016.06.014

中图分类号:V 448.2

文献标志码:A

文章编号:1007-449X(2016)06-0109-08