消纳大规模风电并网的多目标鲁棒调度

王中夫，华栋

(华南理工大学 电力学院，广东 广州 510640)



消纳大规模风电并网的多目标鲁棒调度

王中夫，华栋

(华南理工大学 电力学院，广东 广州 510640)

摘要：考虑风电在波动范围内的所有误差场景，建立了预测场景下最优地适应所有误差场景的多目标鲁棒调度模型。一方面通过采用极限场景法识别出有效场景，使模型得到了简化；另一方面通过模糊评价法将多目标问题转化成单目标问题，目标函数取2个目标的满意度的平均值。最后在12台机组系统上进行算例分析，通过比较传统调度和鲁棒调度的功率缺额，证明了鲁棒调度能更好地适应风电的不确定性，同时也验证了基于模糊评价法的多目标优化能同时兼顾经济和环保两方面因素，使两者均获得较高的满意度。

关键词：风电功率不确定性；鲁棒调度；极限场景；多目标优化

绿色低碳将成为今后我国电力增长的主要形式，风电是我国实现节能减排和2020年非化石能源发展目标的最重要的可再生能源。截至2015年，我国累计风电装机容量达到145.104GW，占全球市场份额的33.6%，居世界首位。传统的电网经济调度建立在对负荷的准确预测上，而风电的间歇性及波动性大大增加了风电功率预测的难度。虽然国内外已经有很多学者对风电功率预测进行了研究，并取得了一定的成果，但仍不能满足工程上的需求。目前，风电预测功率误差控制在20%左右，远大于负荷预测的误差控制，这给电力系统经济调度带来了相当大的困难[1-3]。

在电力系统调度中，处理风电不确定性问题主要有两种方法。其一，分配发电功率来满足负荷，并留有足够的备用容量来满足风电的不确定性[4-6]。这种强加备用的方法原理简单，容易实现，在以往的电力系统调度中得到了广泛的应用。但是这种方法过于保守，而且当风电功率变化较大时，由于机组的爬坡率约束，电网仍会在一定时间内出现容量不足的情况。其二，采用随机优化技术处理风电的不确定性[7-8]。随机优化技术能获得统计意义上的最优期望成本，但为保证计算的准确性，需考虑海量场景，因此难以工程应用。

目前，鲁棒优化受到了广泛的关注。鲁棒优化通过预计各种可能出现的误差场景，建立优化模型，保证调度方案能适应所有的误差场景，当系统发生扰动时，仍能保证系统稳定运行。可见，鲁棒优化对不确定性因素具有一定的适应能力。文献[9]提出基于两阶段零和博弈的鲁棒经济调度方法，并应用于包括风力发电和电动汽车的经济调度；文献[10-11]提出鲁棒可行性约束的经济调度的整体框架和割平面算法，并讨论鲁棒备用整定、机组组合方法的有效性；文献[12]以发电成本最小为目标函数，建立计及电力系统等效负荷的鲁棒超前调度模型；文献[9-12]分别从不同的切入点建立鲁棒调度模型，并通过算例验证了各自模型在应对间歇性能源波动时的可行性，但风电场数目变多时，模型的复杂程度将急剧上升，极大地降低了计算效率；文章[13]提出了一种基于极限场景法的机组组合模型，该方法很好地解决了风电场数目变多时模型复杂度急剧上升的问题，但该文章没有将鲁棒调度结果与传统调度结果进行对比。

另一方面，传统经济调度只追求经济效益，即单目标优化问题。考虑到火电机组在发电过程中排放大量的污染物，不仅破坏生态环境，还对人类健康造成不利影响；因而在电力系统优化调度中，兼顾经济效益与节能减排成为共识。多目标优化问题往往不存在绝对的最优解，因为各个目标可能存在着矛盾，所以多目标的问题关键在于寻求目标之间的一个平衡点，从而得到一个相对合理的有效解。传统解决多目标优化问题一般是通过评价函数法将多目标转化为单目标优化问题，比较常见的类似线性加权法、平方和加权法、理想点法等[14-16]。这种处理方法在分配加权系数时有较大的主观性及随意性，而且各目标之间的单位不一致，不易直接作比较。

在已有的研究基础上，本文基于极限场景法建立了多目标鲁棒调度模型。鲁棒调度考虑了风电在波动范围内的所有误差场景，这保证了电网调度的鲁棒性。同时本文采用模糊评价法处理多目标问题，使调度方案能兼顾经济和环保两方面因素。

1鲁棒调度的场景描述

鲁棒性在控制理论中表征控制系统对特征或参数摄动的不敏感性，本文将鲁棒性引申为对不确定因素的调度方案及其性能的抗干扰能力，即鲁棒性越强，调度方案的抗干扰能力越强。所以，鲁棒调度可以表述为：对信息掌握不完全的电力系统进行调度时，该调度方式能够适应所有可能出现的运行情况，并消除不确定性因素所造成的扰动，在保证电力系统安全、稳定运行的前提下，得到尽量满足发电成本最小化的发电调度方案。

电力系统不确定因素有很多，本文主要处理风电出力的不确定因素。随着风电的大力发展，风电比重在逐年上升，这种不确定因素对电力系统造成的影响也越来越严重。对于含大规模风电并网的调度问题，假设有J个风电场，在某个调度时段风电场可能出现的一组出力集合记为场景si，即

si=[Pw(1),Pw(2),…,Pw(j),…,Pw(J)].(1)

式中：Pw(j)∈[Pw,min(j)，Pw,max(j)]，Pw(j)、Pw,max(j)、Pw,min(j)为第j个风电场的实际出力及其波动上下限。

由于风电出力在波动范围内是连续随机的，假设有Ns个误差场景，则Ns→∞。本文将1天分为96个调度时段h，每个h的时间间距为15 min。记s0为预测场景，在某个h，当间歇性能源出力偏离预测值，场景si将偏离预测场景s0，则称si为误差场景，S为误差场景集，即S=[s1，s2，…，si，…，sNs]。此时如果仍采用预测场景s0下的发电计划P(s0,h)，系统将产生功率缺额，对电网造成不利的影响。故应调整常规机组的出力以平衡这部分功率缺额，误差场景si下满足功率平衡的计划发电出力记为P(si,h)。

其中：

(2)

(3)

式中：P(s0,n,h)、P(si,n,h)分别为预测场景及误差场景下时段h时第n台常规机组的计划出力；N为常规机组数。为了保证对间歇性能源具备足够强的跟随能力，场景之间的过渡将受到爬坡速率的约束。包括从预测场景过渡到任意一个误差场景以及任意2个误差场景之间的过渡。

2含大规模风电并网的鲁棒调度模型

采用预测场景下最小化发电成本作为鲁棒调度模型的目标函数。鲁棒调度的约束方程包括预测和误差场景下的约束方程、场景之间的过渡约束这3个部分。假设研究对象有N台常规机组(火电、水电和燃气机组)，J个风电场。h=1,2,…,H，H为总调度时段数；场景个数i=1,2,…,Ns；常规机组数n=1,2,…,N；风电场个数j=1,2,…,J；Pg、Pw分别记为常规机组、风电场的输出功率。

2.1目标函数

在本文调度模型中，考虑预测场景下火电与气电的发电成本F1作为经济目标，如式(4)所示，火电运行成本为以机组实际出力为决策变量的二次函数，其中，单个调度时段h内的成本特性系数分别为an、bn、cn，P(n,h)为时段h内火电机组n的输出功率。假设不考虑水电的运行成本，可以得到：

(4)

考虑综合污染物排放量F2作为环保目标，采用与经济目标类似的二次函数模型，如式(5)所示，单个调度时段h内的αn、βn、γn为污染物排放系数。

(5)

2.2燃气机组发电量约束

燃气机组发电量约束为

(6)

式中：Δh为调度时段间隔；Ggas为燃气机组的台数；Wgas,max为气电机组最大燃气储存量决定的气电机组容许的最大发电量。

2.3水电机组发电量约束

水电机组发电量约束为

(7)

式中：GH为水电机组的台数；WH,max为调度周期内水电机组允许的发电量上限。水电机组出力受库容，气候等因素影响。

2.4预测场景下的约束方程

预测场景下的约束方程为：

(8)

(9)

(10)

(11)

(12)

式(8)为功率平衡约束，其中Pw(j,h)为时段h内风电场j的输出功率，PL(h)为时段h的负荷水平；式(9)要求各个调度时段下系统留有一定量的旋转备用，其中Sr为负荷对旋转备用的需求，Pmax(n)为火电机组n的出力上限；式(10)、式(11)分别为火电机组出力的上下限约束及调节速率约束，其中rd(n)、ru(n)分别为火电机组n每分钟的最大下调量及最大上调量，调度时段的时间间隔t15=15 min；式(12)为线路潮流约束，其中γg(n,l)、γw(j,l)分别为火电机组n、风电场j在线路l上的功率分布因子，L(l)为线路流量限制。

2.5误差场景下的约束方程

误差场景下的约束与预测场景下的约束相似，区别在于上述的约束方程中，各类型机组出力全部为误差场景下的出力。式(13)为误差场景si下满足功率平衡约束，与式(8)对应，其中P(si,n,h)、Pw(si,j,h)分别为误差场景si下时段h内火电机组n、风电场j的输出功率。同理可得误差场景下的其余约束方程，此处不再赘述。

(13)

2.6场景之间的过渡约束

场景之间的过渡约束为：

(14)

(15)

式中：i′=1,2,…,Ns；tc为场景过渡时间，通常取tc=2.5min。

式(14)要求系统在调整时间tc内从预测场景下的运行点P(s0,n,h)过渡到误差场景下的运行点P(si,n,h)；式(15)要求系统在调整时间tc内完成任意误差场景之间的过渡；si′是与si相邻的任意误差场景。

3关键技术

3.1识别有效场景

为保证调度的安全性，发电计划需适应所有可能出现的误差场景。由于误差场景个数太多，需要从中刷选出有效的场景。场景集的选择是鲁棒调度的一个关键问题。蒙特卡洛仿真法采用概率分布的方法选择场景集具有统计意义上的合理性，但选择出的场景集在应对风电场波动区间时不具有完全的代表性。通常通过给定一个小于1的置信概率来获取风电的波动范围，即极限场景集。该极限场景集忽略了某些小概率的极端波动情况，使调度方案能适应绝大部分的风电波动，并能得到相对较优的发电成本，提高算法的计算速度。因此可以认为模型的解对风电适应力的强弱很大程度上取决于选取的置信区间大小，置信区间选得越大，则将以损失较大的经济性为代价，换取常规机组对风电的不确定性的适应能力，置信区间的选取应综合风电适应性与经济性综合进行考虑。文献[13]证明了只要模型的解能适应极限场景，则必然能适应波动区间内所有的误差场景。换言之，在处理风电场波动区间时，极限场景法具有完全的代表性。以2个风电场为例，极限场景集的选取方法如图1所示。

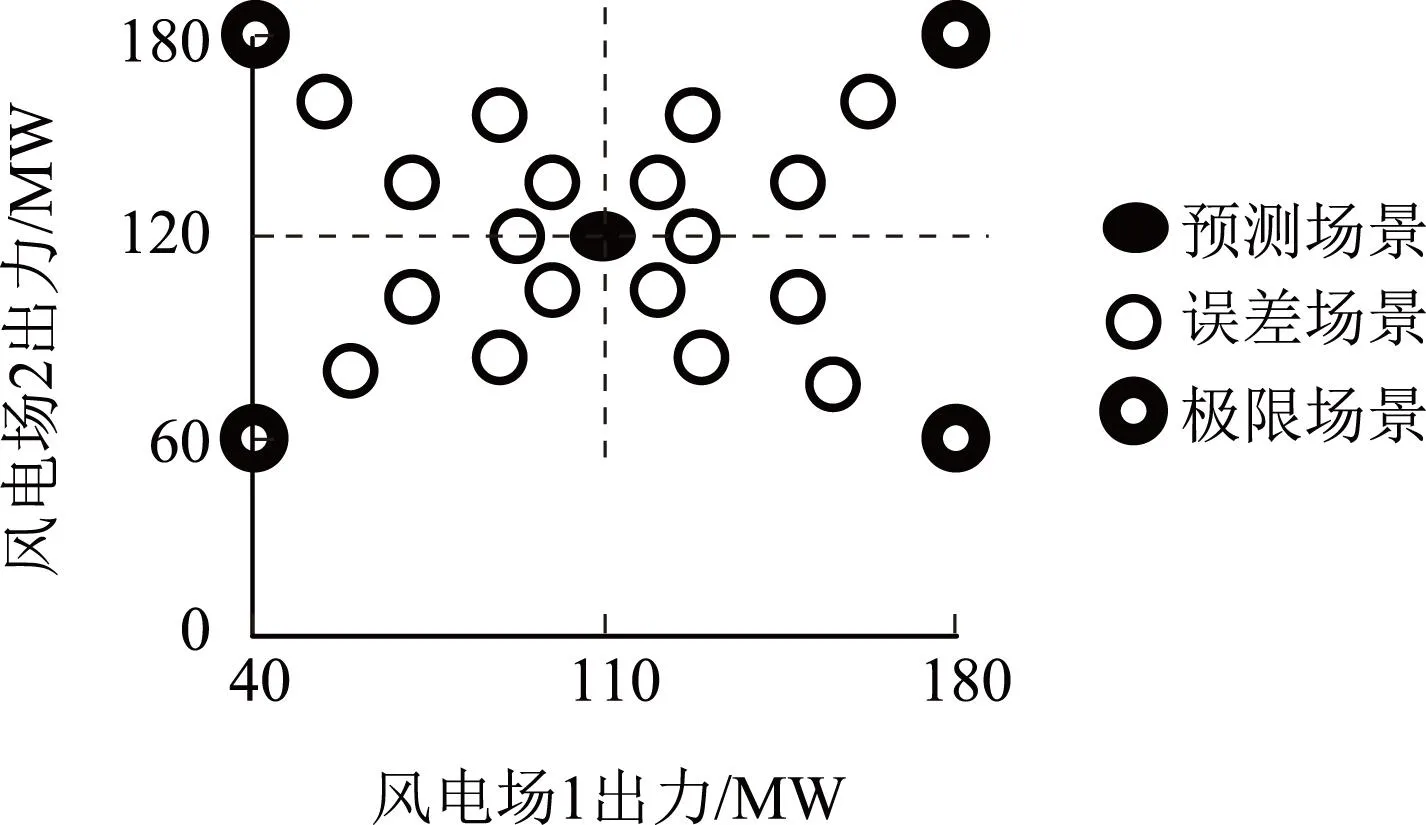
图1　极限场景的选择方法

风电的出力波动主要对电网调度造成两方面的影响：其一，弃风和切负荷损失，这体现在式(8)的功率平衡约束；其二，线路潮流越限，这体现在式(12)的线路潮流约束。为保证调度的安全性，需保证式(10)和式(11)在风电波动区间内均满足要求。

综上所述，调度模型以式(4)作为目标函数；约束方程包括式(8)与式(13)所示的预测场景和极限场景下的功率平衡约束、式(9)所示的旋转备用约束、式(10)和式(11)所示的火电机组运行约束、式(12)所示的预测场景和极限场景下的线路潮流约束。

3.2模糊评价法

模糊评价法是一种基于模糊数学的综合评标方法，是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法。相对于确定性的评价函数，采用模糊评价法能更好地处理目标之间的矛盾关系。本文采用模糊评价法处理多目标优化问题，通过确定目标的隶属度函数将确定性问题模糊化，综合各个目标的满意度，将多目标优化问题转化成单目标优化问题[17-18]。

3.2.1构造目标函数的隶属度函数

对目标函数进行模糊化处理，确定隶属度函数是一个关键问题。隶属度函数有4种函数形式，分别是正太分布、梯形分布、岭形分布、抛物形分布。在本文模型中，发电成本越小，污染物排放量越小，相应的满意度应该越大，目标的隶属度也应变大。所以，本文的2个目标函数均采用降半直线型(属于梯形分布)作为其隶属度函数。具体形式为：

(16)

(17)

式中：θ(F1)和θ(F2)分别为各目标函数的隶属度函数；F′1和F′2为各目标函数的理想值；ΔF1和ΔF2为各隶属度函数的伸缩值。给定参数F′1和F′2时，需要保证F′1≤F1和F′2≤F2，此时，θ(F1)∈[0,1]，θ(F2)∈[0,1]。

3.2.2将模型转化为单目标优化问题

θ(F1)和θ(F2)又称为决策者对各目标的满意程度(数值为1表示完全满意)。本文提出采用2个目标的满意度的平均值作为模型的目标函数，即：

(18)

采用式(18)作为目标函数，则原问题变为求θ最大的过程，即将多目标优化问题化成了单目标优化问题。需要指出的是，在迭代过程中，需要保证θ∈[0,1]。

3.3求解算法

根据所建立的鲁棒调度模型可知，待求解的是一个大规模的非线性优化问题。原-对偶内点法是求解大规模线性优化问题的有效工具，随着问题规模的增大，迭代次数不会有明显变化。因此，本文采用原-对偶内点法该优化问题[19]。一般而言，可用下述数学表达式对非线性规划问题进行描述。

(19)

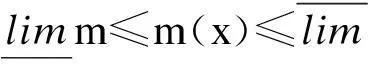
表1单个调度时段h内12台机组系统的各机组参数

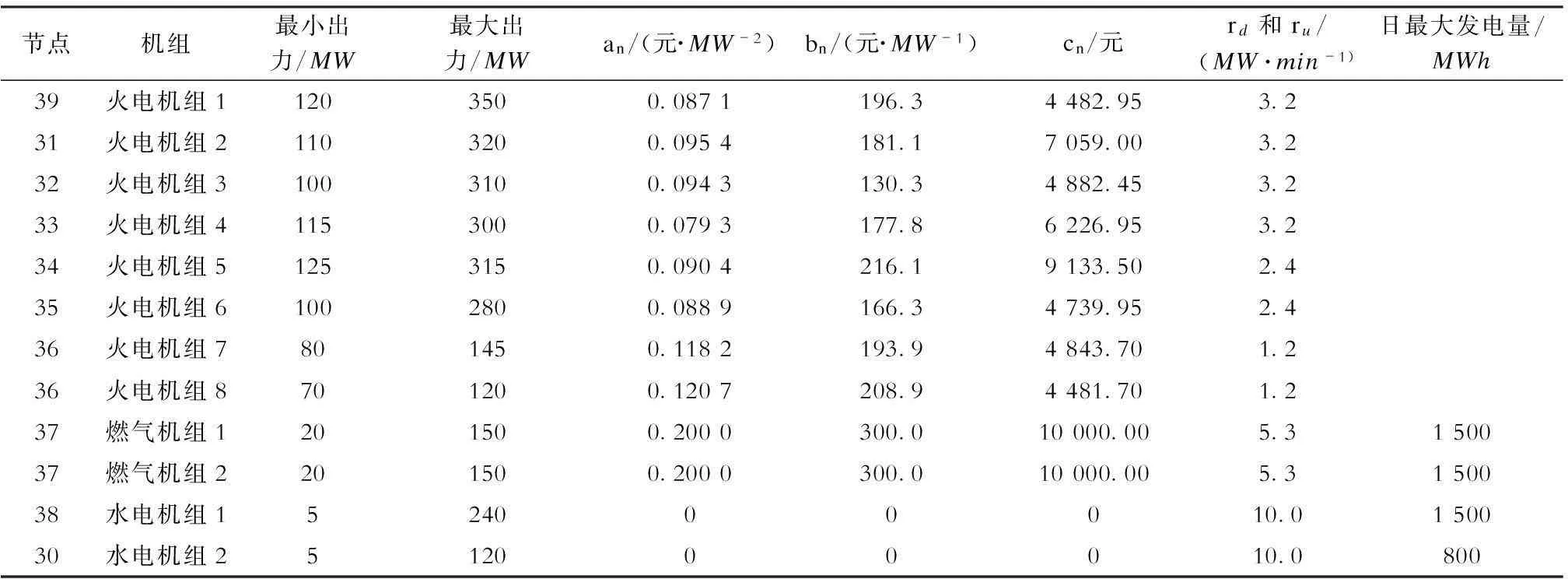
节点机组最小出力/MW最大出力/MWan/(元·MW-2)bn/(元·MW-1)cn/元rd和ru/(MW·min-1)日最大发电量/MWh39火电机组11203500.0871196.34482.953.231火电机组21103200.0954181.17059.003.232火电机组31003100.0943130.34882.453.233火电机组41153000.0793177.86226.953.234火电机组51253150.0904216.19133.502.435火电机组61002800.0889166.34739.952.436火电机组7801450.1182193.94843.701.236火电机组8701200.1207208.94481.701.237燃气机组1201500.2000300.010000.005.3150037燃气机组2201500.2000300.010000.005.3150038水电机组1524000010.0150030水电机组2512000010.0800

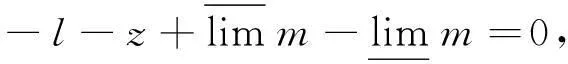
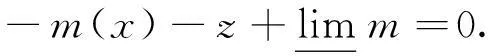
(20)

式中：μ为壁垒参数，其中μk为壁垒参数迭代了k次，当k足够大时，μk应逐渐趋于0；p为不等式约束的个数；l与z为原变量。

当数学模型中只含有等式约束时，等式约束可以通过拉格朗日函数，如式(21)所示，引入到目标函数中，原规划可简化为无约束规划问题，而拉格朗日-牛顿法可以很好地求解这类无约束规划问题。

(21)

式中：λ、π与ν为对偶变量，也就是通常所说的拉格朗日乘子向量；Lμ(y)为拉格朗日函数，当拉格朗日函数Lμ(y)对式(21)中各变量的一阶导函数取得零值时，即满足KKT条件，可取得最优解。原-对偶内点法算法流程图如图2所示。

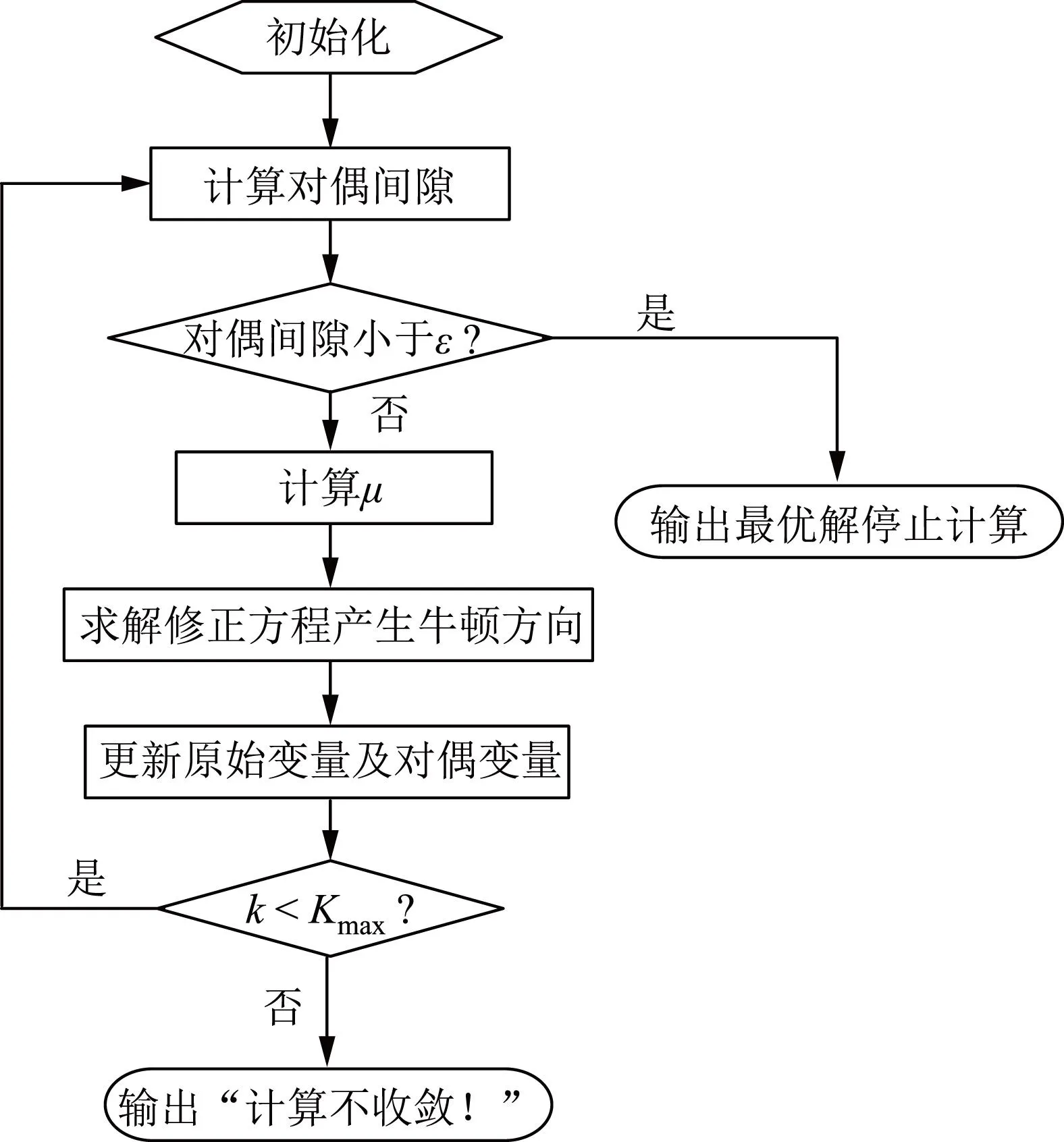
k—已迭代次数；Kmax—最大迭代次数；ε—人为给定的极小值，一般取1×10-6。图2　原-对偶内点法的求解步骤

4实例分析

4.1算例描述

采用本文方法对IEEE39节点系统进行一天内96个调度时段的计算，算例系统中包含8台火电机组、2台水电机组、2台燃气机组和5个风电场，其中7号火电机组与8号火电机组同属一个电厂在节点36处并网，2台燃气机组同属一个电厂在节点37处并网。5个风电场分别于节点30、32、33、34、35处接入，风电预测出力比为10.55%(风电日平均出力与日平均负荷的比率)，采用原-对偶内点法求解模型，使用MATLAB软件进行仿真。算例的12台机组系统的各机组参数见表1，未来一天的负荷预测和风电功率预测值如图3所示，风电功率在预测值±25%的区间内波动。

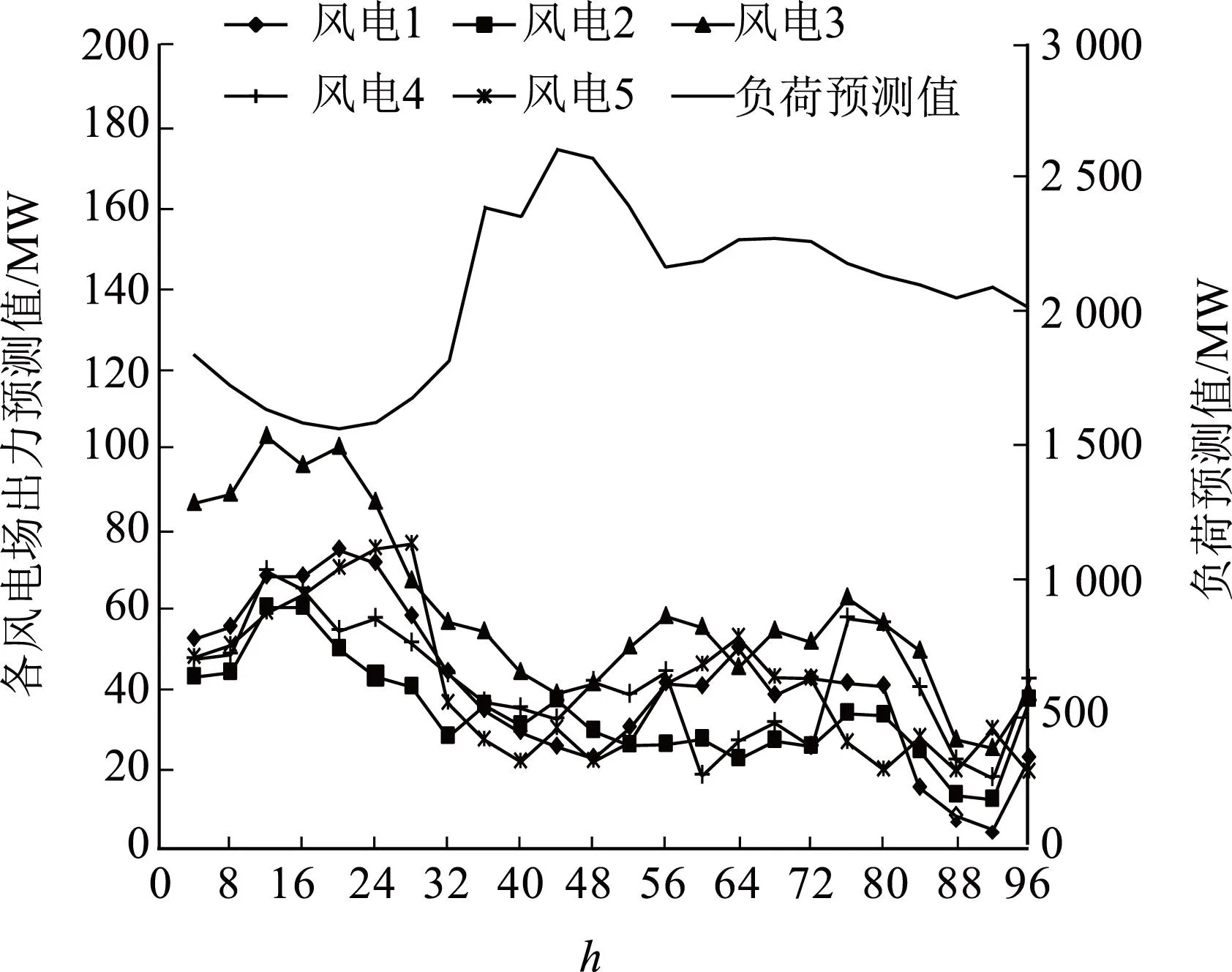
图3　负荷预测和风电功率预测

4.2调度方法对比

传统调度方式未考虑风电波动性对经济调度的影响，直接将风电的预测出力作为其经济调度出力，在极端场景下可能出现功率缺额。而鲁棒调度方式考虑了风电波动范围内的所有误差场景，避免了系统出现有功缺额。为了直观地比较2种调度方法消纳风电的能力，此处只考虑式(4)所示的经济目标，即单一目标函数。在此基础上分别采用2种调度方法对12台机组系统进行调度计算，得到基于鲁棒调度方法制定的发电计划，如图4所示。

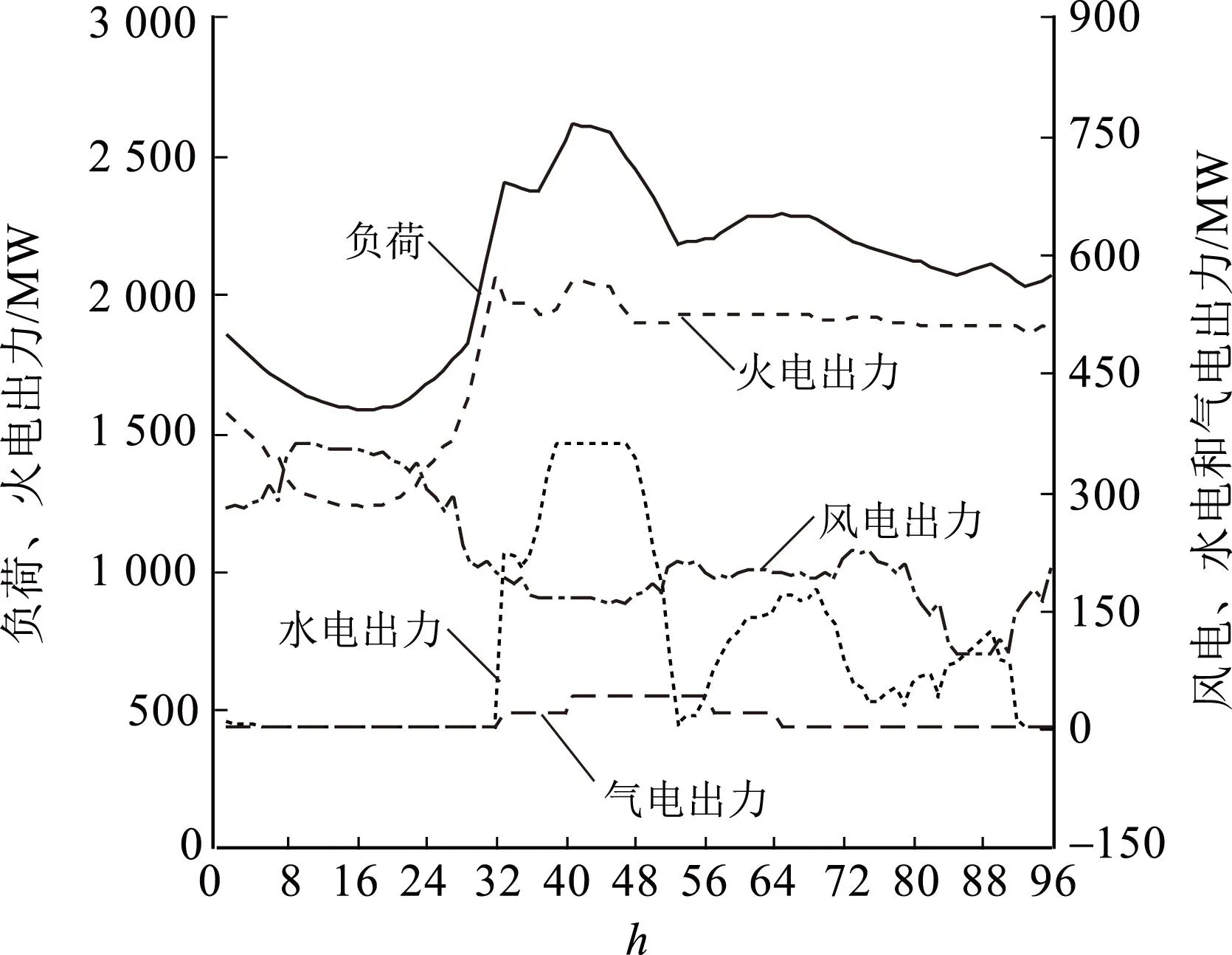
图4　鲁棒经济调度出力方案

考虑到净负荷值(负荷减去风电出力值)在10:00:00—14:00:00时最大，分析系统在此期间(共16个时段)下的功率缺额具有代表性。以其中第3个时段(h=43)为例，风电的出力范围为(162.651±40.66) MW，根据表2，在调整时间tm内，传统调度方式的最大下调、上调功率分别为Pd与Pu：

式中：h=43；Pmax(n)为某机组的出力上限；Pmin(n)为其出力下限；P(n,h)为其实际出力。极限场景下风电场出力波动±40.66MW。为确保系统功率平衡，系统需要调整出力。传统调度最大下调功率Pd=100MW，最大上调功率Pu=27.33MW。故时段h=43时将产生13.33MW的功率缺额。使用相同的方法计算缺额功率，调整时间tm内，鲁棒调度方式的上调容量能力与下调容量能力分别为40.66MW、100MW，系统不会出现功率缺额问题。

表22种调度方式的结果(h=43)

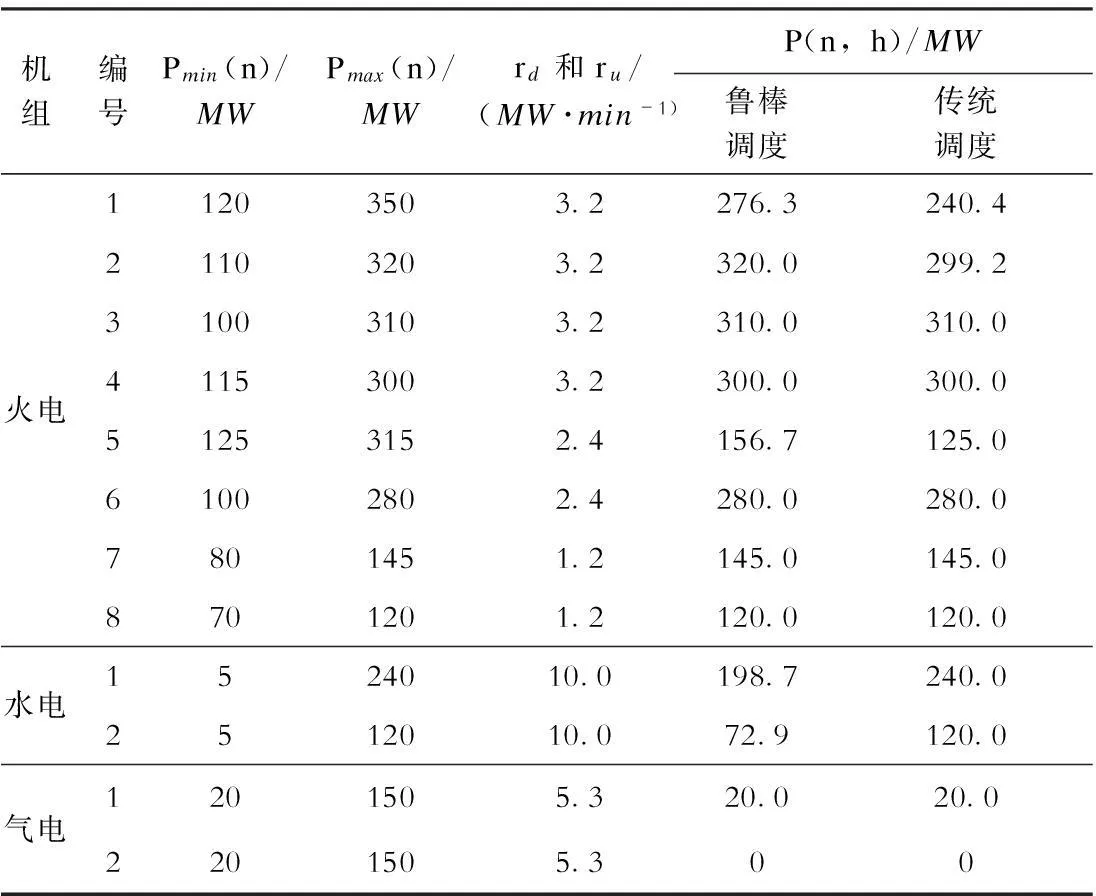
机组编号Pmin(n)/MWPmax(n)/MWrd和ru/(MW·min-1)P(n,h)/MW鲁棒调度传统调度火电1234567812011010011512510080703503203103003152801451203.23.23.23.22.42.41.21.2276.3320.0310.0300.0156.7280.0145.0120.0240.4299.2310.0300.0125.0280.0145.0120.0水电125524012010.010.0198.772.9240.0120.0气电1201505.320.020.02201505.300

根据上面的思路，分别计算2种调度方式在所述16个调度时段可能出现的最大功率缺额，见表3。其中功率缺额大于零表示发电过剩，反之为发电不足。表4为2种调度方式的性能比较。可见传统调度方式在某些时段将出现功率缺额，而鲁棒调度方式则是以损失经济性为代价，换取对间歇性能源不确定性的适应能力。

表32种方法可能出现的最大功率缺额统计

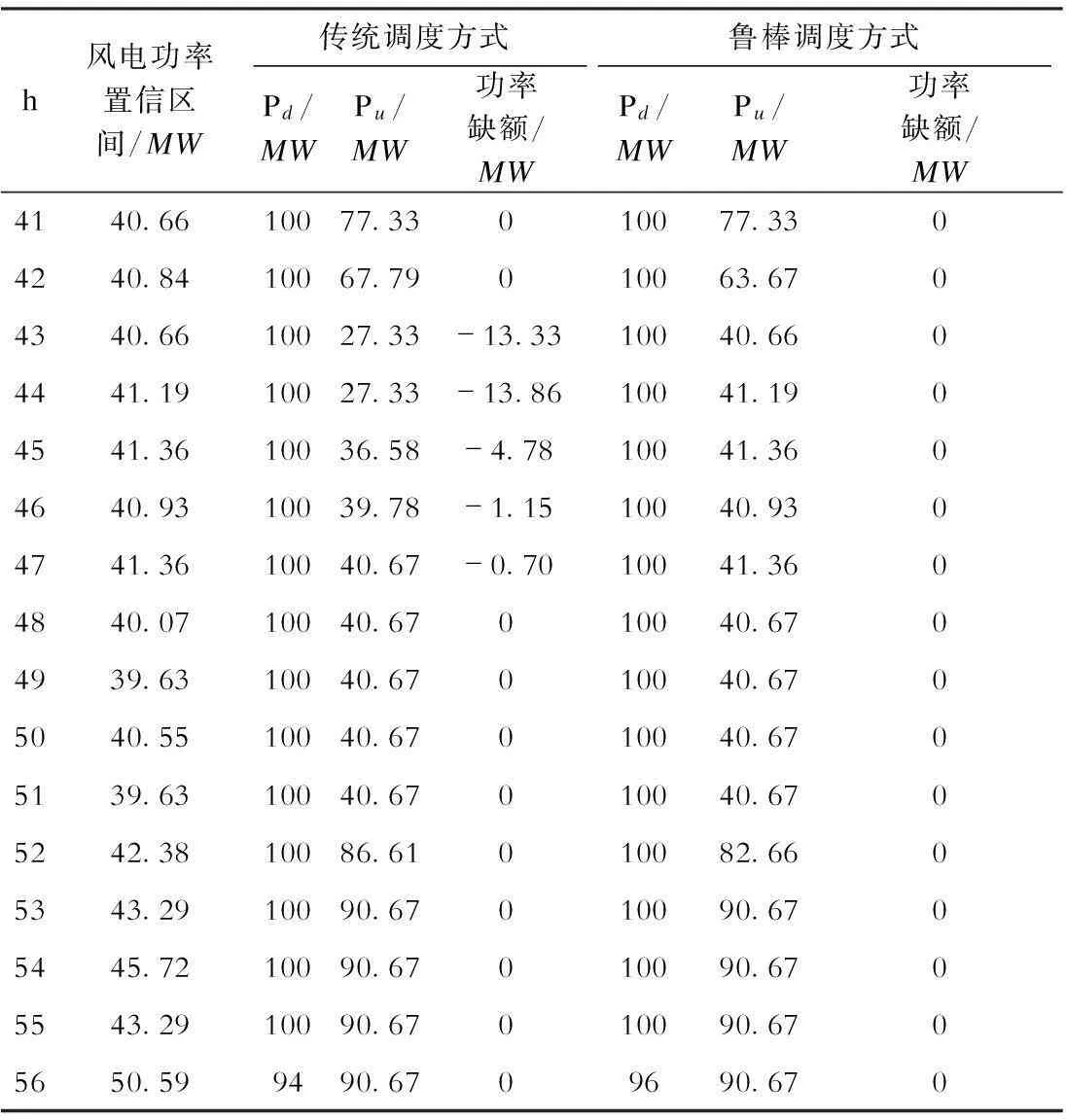
h风电功率置信区间/MW传统调度方式Pd/MWPu/MW功率缺额/MW鲁棒调度方式Pd/MWPu/MW功率缺额/MW4140.6610077.33010077.3304240.8410067.79010063.6704340.6610027.33-13.3310040.6604441.1910027.33-13.8610041.1904541.3610036.58-4.7810041.3604640.9310039.78-1.1510040.9304741.3610040.67-0.7010041.3604840.0710040.67010040.6704939.6310040.67010040.6705040.5510040.67010040.6705139.6310040.67010040.6705242.3810086.61010082.6605343.2910090.67010090.6705445.7210090.67010090.6705543.2910090.67010090.6705650.599490.6709690.670

表42种调度方式的优化性能比较(h=43)

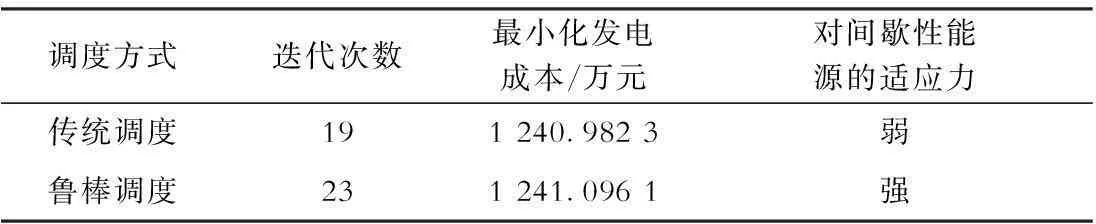
调度方式迭代次数最小化发电成本/万元对间歇性能源的适应力传统调度191240.9823弱鲁棒调度231241.0961强

4.3多目标优化结果

下面考虑经济和环保两方面因素，进行多目标的优化。采用模糊评价法处理多目标问题时，首先设置几个关键的参数。

a)发电成本理想值F′1，污染物排放量理想值F′2。 以发电成本最小的单目标优化问题的最优解为F′1，F′1=1 241.096 1 万元；以污染物排放量最小的单目标优化问题的最优解为F′2=2 348.679 t。

b)伸缩值ΔF1和ΔF2的设置。伸缩值是一个较为灵活的参数，根据不同的决策需要可以设置不同的伸缩值，一般在0和1之间取值。为了保证初始迭代时，满足θ(F1)∈(0,1)及θ(F2)∈(0,1)。本文取ΔF1=0.03×F′1=37.232 9 万元，ΔF2=0.065×F′2= 152.664 t。

根据上述的参数设置进行多目标优化，目标函数的满意度收敛曲线如图5所示。2条曲线变化情况相似，迭代前期曲线平缓上升，当迭代步数达到5次时，满意度快速增大，在迭代步数达到15次时曲线趋于平缓并收敛于一个确定的值。其中，发电成本的满意度收敛于0.763，污染物排放量的满意度为0.804，最终的平均满意度为0.784。

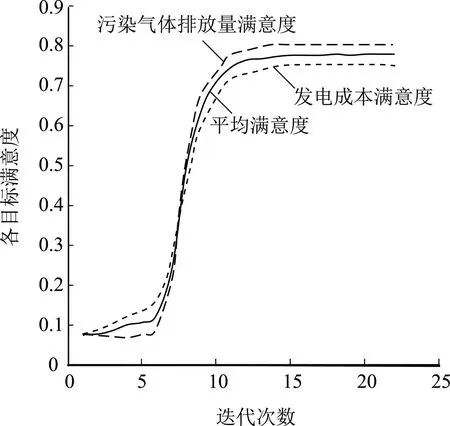
图5　目标函数满意度收敛曲线

将该优化结果与2个单目标优化结果相比较，结果见表5。

表5各种优化方式的优化结果比较(h=43)

优化方式发电成本F1/万元θ(F1)污染气体排放量F2/tθ(F2)平均满意度发电成本最小1241.096113486.7920.2550.627污染气体排放量最小1267.53520.2902348.67910.645多目标优化1249.90920.7632647.7490.8040.784

从表5可以发现：a)发电成本最小的优化方式中，发电成本的满意度为1，污染气体排放量的满意度仅为0.255，可见该优化方式为了追求经济性而忽略了污染物排放的问题；b)基于模糊评价法的多目标优化方式中，发电成本的满意度与污染物排放量的满意度均大于0.75，因此该方法较好地兼顾2个优化目标，使得调度结果的经济和环保双方面均获得较高的满意度。此外，决策者可以通过修改伸缩值来改变优化的性能，体现了决策者的决策偏向及意愿。

5结论

为解决大规模风电并网下的经济调度问题，本文采用场景法描述风电的不确定性，并考虑经济和环保两方面因素，建立了消纳大规模风电的多目标鲁棒调度模型。算例结果表明：a)当风电波动较大时，传统调度方式在某些时段可能出现功率缺额，鲁棒调度方式则可以通过调整常火电机组出力使系统功率迅速恢复平衡；b)传统调度方式更具有经济性，鲁棒调度方式则是以损失经济性为代价换取对风电不确定性的适应能力；c)模糊评价法能较好地兼顾2个优化目标，使得调度结果的经济和环保双方面均获得较高的满意度。

综上，本文方法对风电的不确定性具有良好的免疫力，且兼顾了节能和环保2个方面，在新能源快速发展的形势下，提供了一种可行的调度方法。

参考文献：

[1] 黄德琥，陈继军，张岚.大规模风电并网对电力系统的影响[J].广东电力，2010，23(7)：27-30.

HUANG Dehu，CHEN Jijun，ZHANG Lan. Impact of Large-scale Wind Power Integration on Power System[J].Guangdong Electric Power，2010，23(7)：27-30.

[2] 张丽英，叶廷路，辛耀中，等.大规模风电接入电网的相关问题及措施[J].中国电机工程学报，2010，30(25)：1-9.ZHANG Liying，YE Tinglu，XIN Yaozhong, et al. Problems and Measures of Power Grid Accommodating Large Scale Wind Power [J].Proceedings of the CSEE，2010，30(25)：1-9.[3] 刘思捷，蔡秋娜.大规模风电接入对电力系统有功调度的影响分析[J].广东电力，2013，26(1)：33-37.

LIU Sijie，CAI Qiuna.Influence Analysis on Active Power Dispatch by Introduction of Large Wind Power[J].Guangdong Electric Power，2013，26(1)：33-37.

[4] 周玮，彭昱，孙辉，等.含风电场的电力系统动态经济调度[J].中国电机工程学报，2009，29(25)：13-18.

ZHOU Wei，PENG Yu，SUN Hui，et al. Dynamic Economic Dispatch in Wind Power Integrated System[J].Proceedings of the CSEE，2009，29(25)：13-18.

[5] TUOHY A，MEIBOM P，DENNY E，et al. Unit Commitment for Systems With Significant Wind Penetration[J].IEEE Transactions on Power Systems，2009，24(2)：592-601.

[6] WANG Jianhui，SHAHIDEHPOUR M，LI Zuyi.Security-constrained Unit Commitment with Volatile Wind Power Generation[J].IEEE Transactions on Power Systems，2008，23(3)：1319-1327.

[7] 龙军，莫群芳，曾建.基于随机规划的含风电场的电力系统节能优化调度策略[J].电网技术，2011，35(9)：133-138.

LONG Jun，MO Qunfang，ZENG Jian.A Stochastic Programming Based Short-term Optimization Scheduling Strategy Considering Energy Conservation for Power System Containing Wind Farms[J].Power System Technology，2011，35(9)：133-138.

[8] 徐立中，杨光亚，许昭.考虑风电随机性的微电网热电联合调度[J].电力系统自动化，2011，35(9)：53-60.

XU Lizhong，YANG Guangya，XU Zhao.Combined Scheduling of Electricity and Heat in A Microgrid with Volatile Wind Power[J].Automation of Electric Power Systems，2011，35(9)：53-60.

[9] MEI Sheng，WANG Yingying，SUN Zhenquan.Robust Economic Dispatch Considering Renewable Generation[J].IEEE Transactions on Power Systems，2011，13(16):1-5.

[10] 魏韡,刘锋,梅生伟.电力系统鲁棒经济调度(一)理论基础[J].电力系统自动化，2013，37(17)：37-43.

WEI Wei，LIU Feng，MEI Shengwei.Robust and Economical Scheduling Methodology for Power Systems (Part One: Theoretical Foundations)[J].Automation of Electric Power Systems，2013，37(17)：37-43.

[11] 魏韡，刘锋，梅生伟.电力系统鲁棒经济调度(二)应用实例[J].电力系统自动化，2013，37(18)：60-67.

WEI Wei，LIU Feng，MEI Shengwei.Robust and Economical Scheduling Methodology for Power Systems (Part Two: Application Examples)[J].Automation of Electric Power Systems，2013，37(18)：60-67.

[12] 杨明，韩学山，王士柏，等.不确定运行条件下电力系统鲁棒调度的基础研究[J].中国电机工程学报，2011，31(增刊)：100-107.

YANG Ming，HAN Xueshan，WANG Shibai，et al. Fundamental Research for Power System Robust Dispatch under Uncertain Operating Condition[J].Proceedings of the CSEE，2011，31(S)：100-107.

[13] 叶荣，陈皓勇，王钢，等.多风电场并网时安全约束机组组合的混合整数规划解法[J].电力系统自动化，2010，34(5)：29-33.

YE Rong，CHEN Haoyong，WANG Gang，et al. A Mixed Integer Programming Method for Security-constrained Unit Commitment with Multiple Wind Farms[J].Automation of Electric Power Systems，2010，34(5)：29-33.

[14] 马小姝，李宇龙，严浪.传统多目标优化方法和多目标遗传算法的比较综述[J].电气传动自动化，2010，32(3)：48-50.MA Xiaoshu，LI Yulong，YAN Lang.Comparison Review of Traditional Multi-objective Optimization Methods and Multi-objective Genetic Algorithm[J].Electric Drive Automation，2010，32(3)：48-50.

[15] ABIDO M A.Multi-objective Particle Swarm Optimization for Environmental/economic Dispatch Problem[J].Electric Power Systems Research，2009，79(7)：1105-1113.

[16] SHADMAND M B，BALOG R S.Multi-objective Optimization and Design of Photovoltaic-wind Hybrid System for Community Smart DC Microgrid[J].IEEE Transactions on Smart Grid，2014，5(5)：2635-2643.

[17] 毛弋，刘文春，张鹏飞.利用模糊算法对电力市场下纯火电系统多目标综合经济负荷进行分配[J].电力系统及其自动化学报，2000，12(6)：22-29.

MAO Yi，LIU Wenchun，ZHANG Pengfei.Using the Fuzzy Algorithm to Thermal Power System with Aims Synthetical Real Power Economic Dispatch in Power Market[J].Proceedings of the EPSA，2000，12(6)：22-29.

[18] 张晓花，赵晋泉，陈星莺.节能减排下含风电场多目标机组组合建模及优化[J].电力系统保护与控制，2011，39(17)：33-39.

ZHANG Xiaohua，ZHAO Jinquan，CHEN Xingying.Multi-objective Unit Commitment Modeling and Optimization for Energy-saving and Emission Reduction in Wind Power Integrated System[J].Power System Protection and Control，2011，39(17)：33-39.

[19] 丁晓莺，韦化.现代内点理论及其在电力系统经济调度中的应用[J].广西大学学报(自然科学版)，2000，25(1)：78-82.

DING Xiaoying，WEI Hua.Application of Modern Interior-point Theory for the Economic Load Dispatch Problem in Power Systems[J].Journal of Guangxi University(Nat Sci Ed)，2000，25(1)：78-82.

Multi-objective Robust Dispatching for Large-scale Wind PowerGrid-connectionAbsorption

WANG Zhongfu, HUA Dong

(SchoolofElectricPower,SouthChinaUniversityofTechnology,Guangzhou,Guangdong510640,China)

Abstract：Consideringallerrorscenariosofwindpowerinfluctuationrange,amulti-objectiverobustdispatchingmodelforexcellentlyadaptstoallerrorscenariosunderpredictionscenarioisestablished.Ontheonehand,extremescenariomethodisusedforidentifyingeffectivescenarioswhichcouldsimplifythemodelandontheotherhand,fuzzyevaluationmethodisusedtochangemulti-objectiveproblemintosingle-objectiveproblemandtakesaveragevalueofdegreeofsatisfactionoftwoobjectsasthetargetfunction.Exampleanalysisiscarriedoutintwelveunitsystems.Comparisonofpowervacancybetweentraditionaldispatchingandrobustdispatchingprovesthatthelatterisabletobetteradaptivetouncertaintyofwindpower.Meanwhile,itisverifiedthatmulti-objectiveoptimizationbasedonfuzzyevaluationmethodcangiveconsiderationtobotheconomyandenvironmentalprotectionandmakesbothsidesobtainhigherdegreeofsatisfaction.

Keywords：uncertaintyofwindpower;robustdispatching；extremescenario;multi-objectiveoptimization

收稿日期：2016-02-19修回日期：2016-04-19

基金项目：国家高技术研究发展计划(863计划)项目(2015AA050201)

doi:10.3969/j.issn.1007-290X.2016.06.007

中图分类号：TM614；TB11

文献标志码：A

文章编号：1007-290X(2016)06-0035-08

作者简介：

王中夫(1992)，男，江西吉安人。在读硕士研究生，主要研究方向为电力系统运行与控制。

华栋(1976)，女，江西南昌人。讲师，工学博士，主要研究方向为电力市场、新能源并网和智能电网技术。

(编辑霍鹏)