基于Lanczos模态分析及密集度分析的发射装置轻量化研究

张英琦,乐贵高,马大为,冯国铜

(南京理工大学 机械工程学院,南京 210094)



基于Lanczos模态分析及密集度分析的发射装置轻量化研究

张英琦,乐贵高,马大为,冯国铜

(南京理工大学 机械工程学院,南京 210094)

摘要:针对某型号多管火箭发射装置轻量化设计,采用有限元法建立其刚柔耦合动力学模型,对轻量化前后的模态响应特性及其火箭弹发射密集度进行对比分析,验证了此轻量化设计的可行性。首先,对Lanczos迭代法在经典的特征值问题中进行了推导求解;其次,建立了某复合材料定向管的有限元模型,计算结果与此定向管样机模态试验结果进行对比分析,结果表明基于Lanczos迭代法的有限元模型求解模态是正确的;最后,根据轻量化设计要求,建立了2种材料火箭炮发射装置的整车有限元模型,采用Lanczos迭代法计算其模态特性,根据模态特性选择合理的射击间隔,并通过对比轻量化前后此发射装置火箭弹的射击密集度,验证了此轻量化设计的可行性。

关键词:多管火箭炮;模态试验;Lanczos迭代法;射击密集度;轻量化设计

多管火箭炮作为面杀伤武器,具有火力猛、威力大、机动灵活、反应迅速等特点,它能够在极短的时间内发射多管火箭炮,给命中目标以毁灭性打击,给敌方心理上造成极大的震憾和威慑作用,在战场上发挥着极其重要的作用[1-2]。轻量化设计是多管火箭炮发射装置的重要发展趋势。在确保不降低战术技术性能的前提下对武器系统进行轻量化设计,是提高作战机动性的主要途径。采用轻金属、新型复合材料是实现多管火箭炮轻量化的主要措施之一。

模态特征能够从质量和刚度特性上反映结构的力学性能,故多管火箭炮发射装置轻量化设计前后的模态特性是其动力学分析的重要基础,对控制和优化火箭炮发射装置的动态特性有着至关重要的作用。目前,我国在振动工程领域取得了很多研究成果,部分理论和实验研究已达到国际先进水平。但是,针对多管火箭炮结构动力学的研究仍有待加强。

本文通过模态分析反映多管火箭炮发射装置的振动特性,从而依据振动特性调节多管火箭炮的合理发射间隔,在满足发射密集度指标的情况下,验证轻量化设计的可行性。

1模态求解基本理论

大型结构的特征值解法[3],主要有矩阵反迭代法、子空间迭代法、里兹向量直接叠加法和Lanczos迭代法等。Lanczos迭代法对n×n阶矩阵进行了数次迭代,可使矩阵三对角化,然后用Sturm定理和二分法求特征值,相应的特征向量可用带移位的反迭代求得。Lanczos迭代法可有效地克服因系统中存在等固有频率或几个固有频率而引起的收敛过慢问题[4]。

系统运动方程:

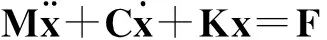
(1)

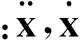
典型的无阻尼模态分析求解的基本方程就是经典的特征值问题:

Kφ-ω2Mφ=0

(2)

式中:φ为系统振型,ω为系统自振频率。

令

ω2=λ-δ

(3)

式中:δ>0,则λ即为正数,这样就将零特征值问题化解成非零特征值问题:

Kφ=(λ-δ)Mφ

(4)

令

(5)

M=LLT

(6)

(7)

y=LTφ

(8)

则式(4)化为

Ay=λy

(9)

寻找正交矩阵Q=(q1q2…qn),使得QTAQ=T,式中:n为正交基个数,T为三对角阵,记为

Lanczos算法递推求解得到(当j=1时,取βj-1=0):

①αj=(qjAqj)。

②残余向量wj=Aqj-βj-1qj-1-αjqj。

③βj=‖wj‖2,qj+1=wj/βj。

式中:j为递推次数。上述递推过程循环计算,可求得标准正交基(q1q2…qn)。采用Lanczos法求得正交变换矩阵Q和对角矩阵T后,可用二分法求解λ和ω。

2复合材料定向管模态分析与试验

2.1复合材料定向管有限元模型

根据某复合材料定向管的结构和材料,模拟其铺层形式,用壳单元建立有限元模型,如图1所示。

图1复合材料定向管有限元模型

复合材料定向管径向由10层玻璃纤维增强树脂基复合材料环向铺层缠绕而成,相邻两铺层之间相互垂直,以45°或-45°斜角铺层。每一层的厚度为0.3mm,3mm厚的玻璃钢定向管划分后的单元共10层,如图2所示。

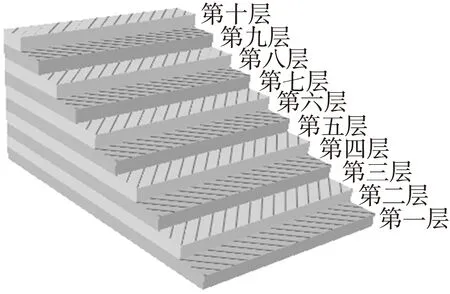
图2　定向管材料铺层

材料参数利用文献[5]中的玻璃纤维增强复合材料的性能参数,如表1所示。表中,ρ为材料密度,E1为纵向弹性模量,E2为横向弹性模量,ν为泊松比,G12为纵横剪切弹性模量,Xt为纵向拉伸强度,Yt为横向拉伸强度,Xc为纵向压缩强度,Yc为横向压缩强度,S为剪切强度。

表1　复合材料定向管材料参数

2.2定向管样机模态试验验证

为验证Lanczos迭代法在有限元模态分析中的准确性,建立了复合材料定向管有限元模型,采用Lanczos迭代法进行模态分析,同时制定了该防空火箭炮定向管样机并进行模态试验。图3和图4为该复合材料定向管试验模型和模态试验测试系统;图5为锤击法模态试验原理框架图;对该复合材料定向管仿真结果与试验结果的前三阶模态进行对比如图6所示。试验过程中力锤在每个测试点上敲击3次对其结果进行平均,对每个点均观察波形和试验自谱,保证相干函数值不低于0.8。

图3　定向管试验几何模型

图4　模态试验测试系统

图5　锤击法模态试验框图

如图6和表2所示,d为模态阶数,fe为计算频率,ft为试验频率,ε为结果偏差。对比定向管前三阶自由模态的仿真结果与试验结果可知,定向管振型一致,振动频率误差均在2%以内,两者吻合度较高,考虑试验测试存在不可控因素及数值解自身的误差,两者的吻合度是令人满意的,表明了有限元模型的正确性。可见,基于Lanczos迭代法的有限元模型求解模态是可靠的,可以为后续的动力学分析提供研究基础。

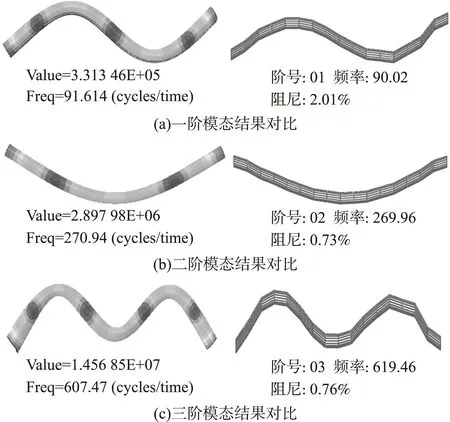
图6　仿真结果与试验结果对比图

dfe/Hzft/Hzε/%191.61490.021.772270.94269.960.363607.47619.461.94

3某多管火箭炮发射装置轻量化设计

3.1某车载多管火箭炮发射装置数值模型

发射装置起竖仰角53°,回转角度为0,采用轮胎和支腿的混合支撑方式,按给定射序发射6枚火箭弹。如图7所示,建立了某型号车载多管火箭炮发射装置的有限元模型及其射序。

图7　车载多管火箭炮有限元模型和射序示意图

仿真过程中的假设条件:

①发射车所处场坪为水平状态,忽略场坪的变化;

②忽略环境因素对发射装置动力学的影响;

③忽略对发射平台动力学影响较小的部件结构,如驾驶室、仪器舱、油箱、变速箱、发动机等部件,按照给定质量参数对整车进行配重;

④认为发射系统各结构部件在火箭弹发射过程中不会塑性变形和断裂,变形均处于弹性变形范围内。

该多管火箭炮发射装置的射击间隔初始设计值为0.7s,射击间隔与系统的模态响应密切相关,应尽量避开发射装置的固有振动频率[6-8],避免火箭炮发射过程中产生共振影响射击密集度。因此,采用2.2节中验证的Lanczos迭代法对发射装置进行模态仿真分析。给出该发射装置的前四阶自由模态如图8所示,发射装置前四阶模态频率及周期如表3所示,最大的第一阶周期为0.619 6s,小于射击间隔初始设计值,表明了该设计值的可行性。

图8　钢结构发射装置前四阶自由模态

df/HzT1/sdf/HzT1/s11.61390.619634.04290.247323.64670.274244.69240.2131

在0.7s发射间隔基础上,通过仿真计算得到6枚火箭弹发射过程中的角速度、角位移响应曲线,限于篇幅,给出6枚火箭弹的俯仰角速度响应曲线如图9所示,轻量化前火箭弹的起始扰动仿真结果如表4所示,表中,t为出筒时刻,ω1为俯仰角速度,φ1为俯仰角位移,ω2为偏航角速度,φ2为偏航角位移。

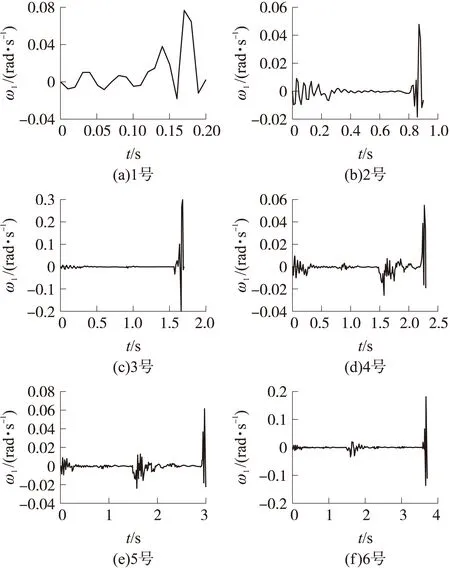
图9　轻量化前火箭炮俯仰角速度响应

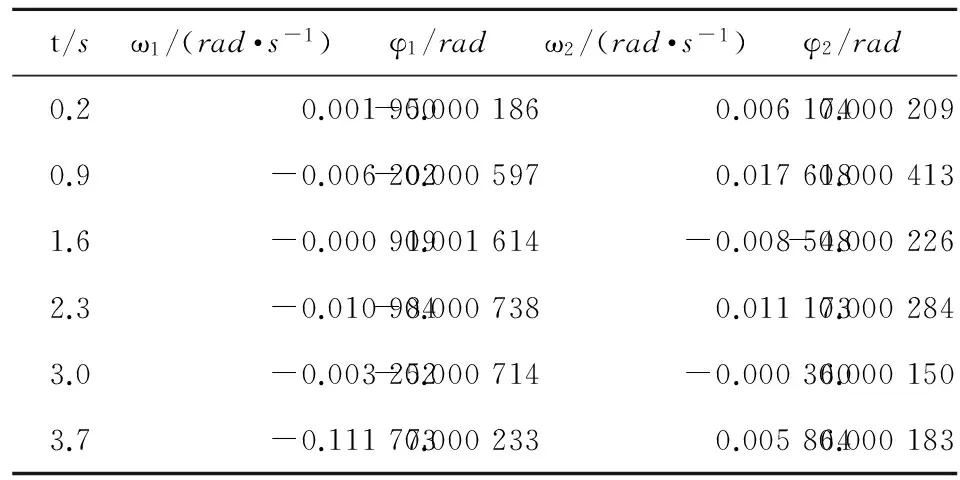
t/sω1/(rad·s-1)φ1/radω2/(rad·s-1)φ2/rad0.20.001950-0.0001860.0061740.0002090.9-0.006202-0.0005970.0176180.0004131.6-0.0009190.001614-0.008548-0.0002262.3-0.010984-0.0007380.0111730.0002843.0-0.003252-0.000714-0.0003600.0001503.7-0.1117730.0002330.0058640.000183

3.2车载多管火箭炮发射装置轻量化设计

3.1节中所示的车载多管火箭炮发射装置,以其轻量化设计要求为背景,将发射箱、上架、下架和回转盘等强度要求不高的部件均由钢材料轻量化为铝合金材料,即为发射装置的轻量化初步设计方案。铝合金材料密度为2 700kg/m3,弹性模量取70GPa,泊松比为0.33。以下对该轻量化设计方案从射击密集度和射击间隔两方面进行可行性验证。

采用2.2节中验证的Lanczos迭代法对轻量化后的发射装置进行模态分析。给出轻量化后发射装置的前四阶自由模态如图10所示,轻量化后发射装置前四阶模态频率及周期如表5所示,轻量化后最大的第一阶周期为0.811 0s,大于0.7s的射击间隔设计值。研究发现,发射装置轻量化后,系统固有特性发生了变化,需要重新确定合理的发射间隔,如发射间隔沿用0.7s,连续发射时,前一发弹对后一发弹的影响明显增大,使后一发火箭弹离轨时的起始扰动增大,使得密集度变差,达不到设计指标要求。因此,需要重新确定发射时间间隔,结合结构模态分析结果,并对比0.9s,1s,1.1s和1.2s的不同发射间隔对起始扰动的影响,确定了1.2s的发射时间间隔,并通过密集度计算对新发射时间间隔进行了验证。

图10　铝合金材料发射装置前四阶自由模态

df/HzT1/sdf/HzT1/s11.23300.811032.88620.346522.18120.458543.13720.3188

将3.1节中数值模型的发射箱、上下架和回转盘等部件赋予铝合金材料属性,仿真计算该装置6枚火箭弹出筒的角速度、角位移响应曲线,限于篇幅仅给出6枚火箭弹的俯仰角速度曲线如图11所示,轻量化后火箭弹的起始扰动仿真结果如表6所示。

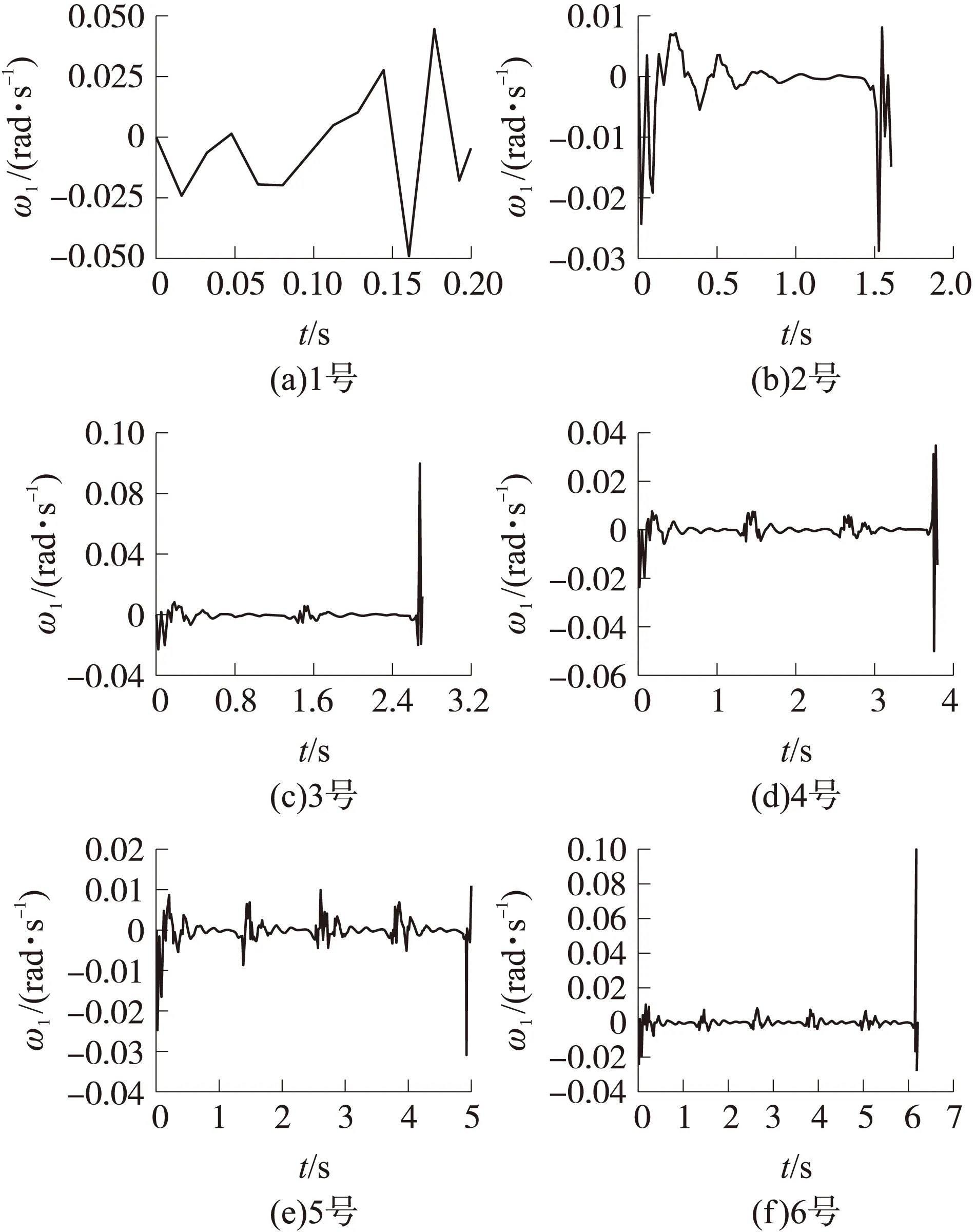
图11　轻量化后火箭炮俯仰角速度响应

t/sω1/(rad·s-1)φ1/radω2/(rad·s-1)φ2/rad0.20.012813-0.0006820.0133670.0004321.4-0.014839-0.0012890.0047530.0002982.60.021244-0.001189-0.0015990.0002723.8-0.010272-0.0013320.0269120.00066350.010787-0.0009730.0184110.0005886.20.007925-0.001304-0.0098160.000119

3.3发射装置轻量化前后密集度计算

多管火箭炮的射击密集度是对火箭弹散布的度量,是火箭炮武器系统的重要技术性能指标,是射击精度的重要组成部分。故发射装置的轻量化设计应该在稳定火箭炮武器发射密集度的基础上进行。

运用3.1节和3.2节中轻量化前后火箭弹起始扰动仿真结果,并通过文献[9],以六自由度刚体弹道模型为基础,综合考虑质量、质量偏心等因素对火箭弹飞行过程及密集度的影响,建立了一般无控火箭弹外弹道模型。采用文献[10～11]中密集度算法编程计算,获得了该发射装置轻量化前后的射击密集度,轻量化前发射装置偏航密集度为1/201rad,距离密集度为1/135rad,轻量化后发射装置偏航密集度为1/190rad,距离密集度为1/110rad。

轻量化未导致射击密集度的降低,且有小幅度提升,满足最大射程密集度设计指标要求。通过对射击密集度和射击间隔指标的分析,可知文中给出的火箭炮发射装置的轻量化设计是可行的。改变发射间隔,在轻量化的基础上密集度也有相应的提高。

4结束语

定向管前三阶自由模态的仿真结果与试验吻合度较高,验证了基于Lanczos迭代法的有限元模型求解模态的正确性。

进行轻量化设计后,通过有限元模态分析,发射装置的最大的第一阶周期为0.811 0s,大于0.7s的射击间隔设计值,考虑发射过程中火箭弹的起始扰动,将轻量化后的发射间隔改为1.2s;进行轻量化设计后,通过改变射击时间间隔,发射装置的密集度有一定的提高。

本文提出的轻量化设计方案能够有效地降低发射装置的质量,通过改变射击时间间隔,减小火箭弹初始扰动,以此提高了射击密集度。

参考文献

[1]张敬.火箭炮的发展及性能提高的途径[J].导弹与航天运载技术,2001(2):58-61.

ZHANG Jing.Development of rocket gun and methods of improving performance[J].Missiles and Space Vehicles,2001(2):58-61.(in Chinese)

[2]CHRISTENSEN D E.Multiple rocket launcher characteristics and simulation technique,AD-A025379[R].1976.

[3]王勖成.有限单元法[M].北京:清华大学出版社,2003.

WANG Xu-cheng.Finite element method[M].Beijing:Tsinghua University Press,2003.(in Chinese)

[4]徐稼轩,郑铁生.结构动力分析的数值方法[M].西安:西安交通大学出版社,1993.

XU Jia-xuan,ZHENG Tie-sheng.Numerical method for dynamic analysis of structures[M].Xi’an:Xi’an Jiaotong University Press,1993.(in Chinese)

[5]蔡德咏,马大为,于存贵,等.复合材料定向管轻量化设计[J].南京理工大学学报,2011,35(2):168-172.

CAI De-yong,MA Da-wei,YU Cun-gui,et al.Light-weight design of composite materials direction tube[J].Journal of Nanjing University of Science and Technology,2011,35(2):168-172.(in Chinese)

[6]潘宏侠,赵彦,陈国光,等.振动对火箭炮密集度影响研究[J].兵工学报,1993,11(4):17-22.

PAN Hong-xia,ZHAO Yan,CHEN Guo-guang,et al.Effects of launcher vibration upon the hitting dispersion of rockets[J].Acta Armamentarii,1993,11(4):17-22.(in Chinese)

[7]贺军义,芮筱亭,王国平,等.提高多管火箭射击密集度射击技术研究[J].振动工程学报,2011,24(6):676-681.

HE Jun-yi,RUI Xiao-ting,WANG Guo-ping,et al.Design technology of improving firing dispersion of MLRS[J].Journal of Vibration Engineering,2011,24(6):676-681.(in Chinese)

[8]杨帆,王国平,芮筱亭,等.射击间隔对多管火箭动态特性的影响[J].南京理工大学学报,2006,30(4):400-403.

YANG Fan,WANG Guo-ping,RUI Xiao-ting,et al.Influence of firing interval on dynamics characteristic of MLRS[J].Journal of Nanjing University of Science and Technology,2006,30(4):400-403.(in Chinese)

[9]徐明友.火箭外弹道学[M].哈尔滨:哈尔滨工业大学出版社,2004.

XU Ming-you.Exterior ballistics of rockets[M].Harbin:Harbin Institute of Technology Press,2004.(in Chinese)

[10]王峰,于存贵,马大为,等.舰载多功能火箭炮射击密集度仿真分析[J].弹箭与制导学报,2006,26(2):737-739.

WANG Feng,YU Cun-gui,MA Da-wei,et al.Simulation research on shooting dispersion of ship-borne multi-function launcher rocket[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(2):737-739.(in Chinese)

[11]李魁武,王宝元.火炮射击密集度研究方法[M].北京:国防工业出版社,2012:24-29.

LI Kui-wu,WANG Bao-yuan.Research methods of gun firing dispersion[M].Beijing:National Defense Industry Press,2012:24-29.(in Chinese)

Lightweight Research of MLRS Based on Modal Analysis With Lanczos-reduce Method and Dispersion Analysis

ZHANG Ying-qi,LE Gui-gao,MA Da-wei,FENG Guo-tong

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

Abstract:To research the lightweight of multiple launcher rocket system(MLRS),the rigid-flexible-coupling dynamic model with finite element method was applied.The modal response and firing dispersion after the lightweight was compared with that before the lightweight respectively,and the feasibility of lightweight was verified.The classical eigenvalue problem was solved by Lanczos-reduce method.The FEM model of composite materials direction tube was built,and the FEM results were compared with the modal test results.The result shows that the modal solved by Lanczos is correct. The FEM models of MLRS of two kinds of materials were built,and the modal characteristics were calculated by using Lanczos.The reasonable firing interval was selected according to modal characteristics.The firing dispersion of rocket after lightweight was compared with that before lightweight.The result shows that the design of lightweight is feasible.

Key words:multiple launcher rocket system;modal test;Lanczos-reduce method;firing dispersion;lightweight design

收稿日期:2015-12-18

作者简介:张英琦(1988- ),女,博士研究生,研究方向为结构动力学。E-mail:zhangyingqi0627@163.com。

中图分类号:TJ303.4

文献标识码:A

文章编号:1004-499X(2016)02-0068-06