基于非定常CFD的俯仰动导数计算方法

伍　彬,陆　韵,周志超,傅建明

(上海机电工程研究所,上海 201100)



基于非定常CFD的俯仰动导数计算方法

伍彬,陆韵,周志超,傅建明

(上海机电工程研究所,上海 201100)

摘要:采用基于N-S方程求解的非定常CFD技术,对俯仰动导数数值计算方法进行了研究。研究了时间步长、内迭代次数、强迫运动幅值、减缩频率对俯仰动导数计算结果的影响。计算了动导数标模在不同马赫数下的俯仰动导数,并与实验结果进行了比较。结果表明,时间步长与减缩频率是影响俯仰动导数计算结果的2个重要因素。给出了俯仰动导数数值计算时间步长与减缩频率选取的一般原则。基于非定常CFD技术的俯仰动导数数值计算方法精度较高,与实验结果吻合良好,具有较高的工程应用价值。

关键词:俯仰动导数;时间步长;内迭代次数;强迫运动振幅;减缩频率

动导数是表征飞行器动态特性的重要参数,对飞行器的稳定性和操纵性有着十分重要的影响。目前,获取动导数的主要方法包括理论估算、风洞实验、飞行实验及数值计算。其中理论估算最为快速方便,但只适用于简单、常规的飞行器,且精度较差,难以满足复杂的现代飞行器的需求。风洞实验可以通过有限自由振动法、强迫运动法和模型自由飞等手段获得飞行器动导数,但面临耗费大、周期长的问题。而飞行实验难度大、周期长、风险高,且不能在飞行器初步设计阶段获得数据,无法对设计起指导作用。随着计算流体力学(CFD,Computational Fluid Dynamics)技术的发展及非定常数值计算精度的提高,采用CFD数值计算的方法获取飞行器动导数是目前较理想、较经济的方法之一。

袁先旭、张涵信[1]等研究了基于CFD的俯仰静、动导数计算,提出了2种辨识方法。孙涛、高正红[2]等基于Euler方程研究了动导数的数值计算方法,以及Ma为1.58的情况下不同减缩频率对动导数计算结果的影响。刘绪[3]、卢学成[4]分别研究了超声速情况下的飞行器动导数数值计算。Despirito[5]和Bhagwandin[6]分别采用锥动法对动导数进行了计算,得到了较好的结果。本文基于N-S方程对飞行器的动导数计算方法开展了研究,以动导数标模[7-8](Basic Finner Missile)为研究对象,采用小振幅强迫运动的方法获取飞行器的俯仰动导数,研究了时间步长、内迭代次数、强迫运动振幅以及减缩频率对动导数计算结果的影响,给出了一般性的结论。计算了动导数标模在不同马赫数下的俯仰动导数,并与实验结果进行了比较。

1动导数计算理论与数值方法

1.1动导数计算理论

以俯仰阻尼动导数计算为例,对动导数的计算方法进行了说明。假设飞行器在俯仰平面内做绕质心的单自由度小振幅强迫运动。强迫运动的具体形式为

(1)

式中:θ为俯仰角,θm为振幅,α为攻角,ω为强迫运动频率,q为俯仰角速度。

飞行器所受的非定常俯仰力矩系数Cm的表达式可以写成[3]:

(2)

将式(2)进行Taylor级数展开并略去高阶项,有:

(3)

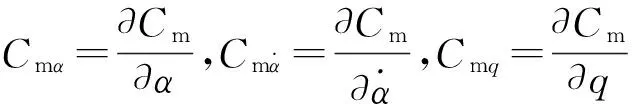
将式(1)代入式(3),合并同类项,有:

(4)

当非定常运动时间足够长时,非定常气动力矩会表现出稳定的周期性,且其周期与强迫运动周期相同,因此非定常俯仰力矩系数也可以写为

Cm=Cm0+Cmssinωt+Cmccosωt

(5)

式中:Cms为正弦项系数,Cmc为余弦项系数。

对比式(4)和式(5),可知:

(6)

非定常俯仰力矩系数随时间的变化规律可以由CFD计算得到,那么Cms和Cmc可以由下式给出:

(7)

式中:N为一个运动周期内的迭代次数。

(8)

1.2数值方法

笛卡尔坐标下,三维N-S方程可以写为

(9)

式中:Q为守恒量;F1,F2,F3为无粘通量;G1,G2,G3为粘性通量。

本文计算时,空间离散采用二阶Roe格式,时间推进采用隐式双时间步推进方法,在时间上也保证二阶精度。湍流模型采用两方程Realizablek-ε模型,该湍流模型能够较好地处理复杂剪切流、漩涡流动、边界层分离、大攻角失速和转捩等状况。强迫运动采用刚性动网格技术实现。

2建模与定常计算结果讨论

2.1几何模型及网格划分

计算模型采用动导数标模,弹径为d,长细比为10。尾翼厚度为0.08d,尾翼前缘倒圆半径为0.004d。具体尺寸见图1。

划分流场网格,第一层网格高度约为0.005 mm,网格总数为280万,物面及对称面网格如图2所示。

图1　计算模型

图2　流场网格

2.2定常计算结果

在非定常计算之前,先进行定常计算,并与实验结果进行比较,以确认定常数值计算的精度,并将定常流场作为非定常计算的初始流场。图3给出了Ma=0.9和Ma=2.5两个状态下的对称面流场马赫数分布云图和等值线图,可以看出,头部激波和底部低速区等典型流动特征都得到了很好的捕捉。

图3　马赫数等值线及物面压力分布

图4给出了Ma=0.6～3.0范围内飞行器的轴向力系数CA、法向力系数斜率CNα和俯仰力矩系数斜率Cmα。从图4可以看出,定常计算的结果与实验结果吻合很好,具有足够的精度,能满足非定常计算的要求。

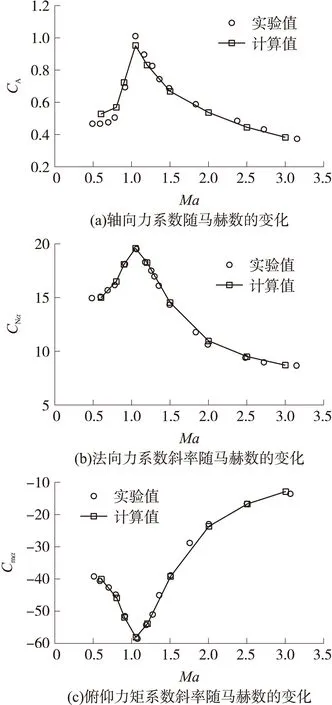
图4　定常气动系数计算值与实验结果比较

3动导数计算影响因素分析

影响动导数计算结果的因素有网格类型、网格数量、湍流模型、非定常时间步长、内迭代次数、强迫运动幅值以及减缩频率等,本文只考虑非定常时间步长、内迭代次数、强迫运动幅值以及减缩频率的影响,对动导数的影响因素进行分析。

3.1时间步长与内迭代次数的影响

定义Δt为非定常计算时间步长,NI为内迭代次数。图5给出了不同时间步长的俯仰力矩系数随攻角的变化结果,图6给出了不同时间步长和内迭代次数的俯仰动导数计算结果。可知,当强迫运动幅值和减缩频域一定时,不同时间步长对应的攻角-俯仰力矩系数迟滞曲线基本相同,但俯仰动导数计算结果区别较大。随着时间步长减小,计算结果相对差别也逐渐减小。Ma=0.9时,相对差别从3%下降到1%;Ma=2.5时,相对差别从2%下降到0.7%。内迭代次数对结果影响较小,当内迭代次数NI≥10时,俯仰阻尼动导数结果趋于稳定,不随内迭代次数的增加而变化。

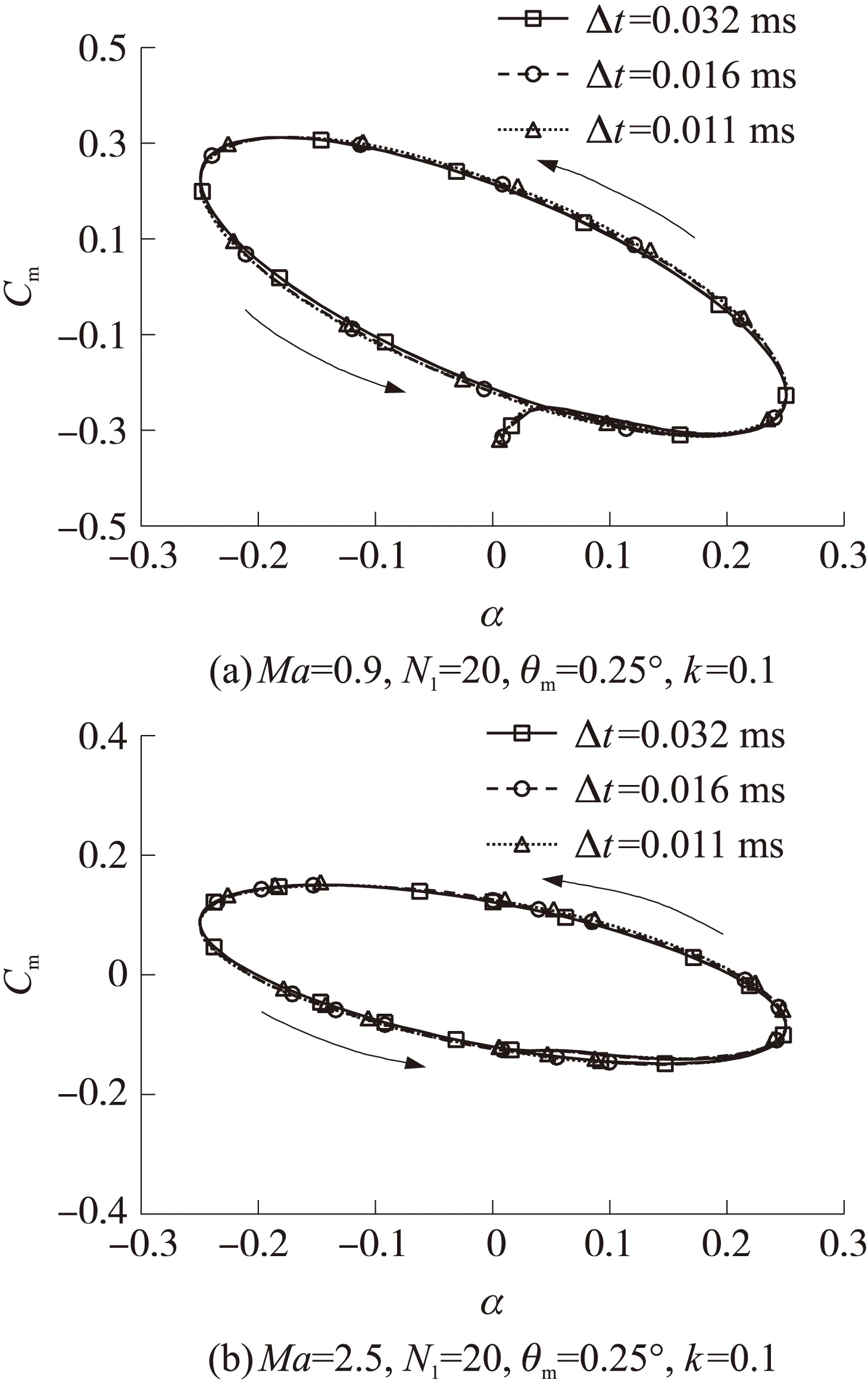
图5　不同时间步长情况下俯仰力矩系数随攻角的变化曲线

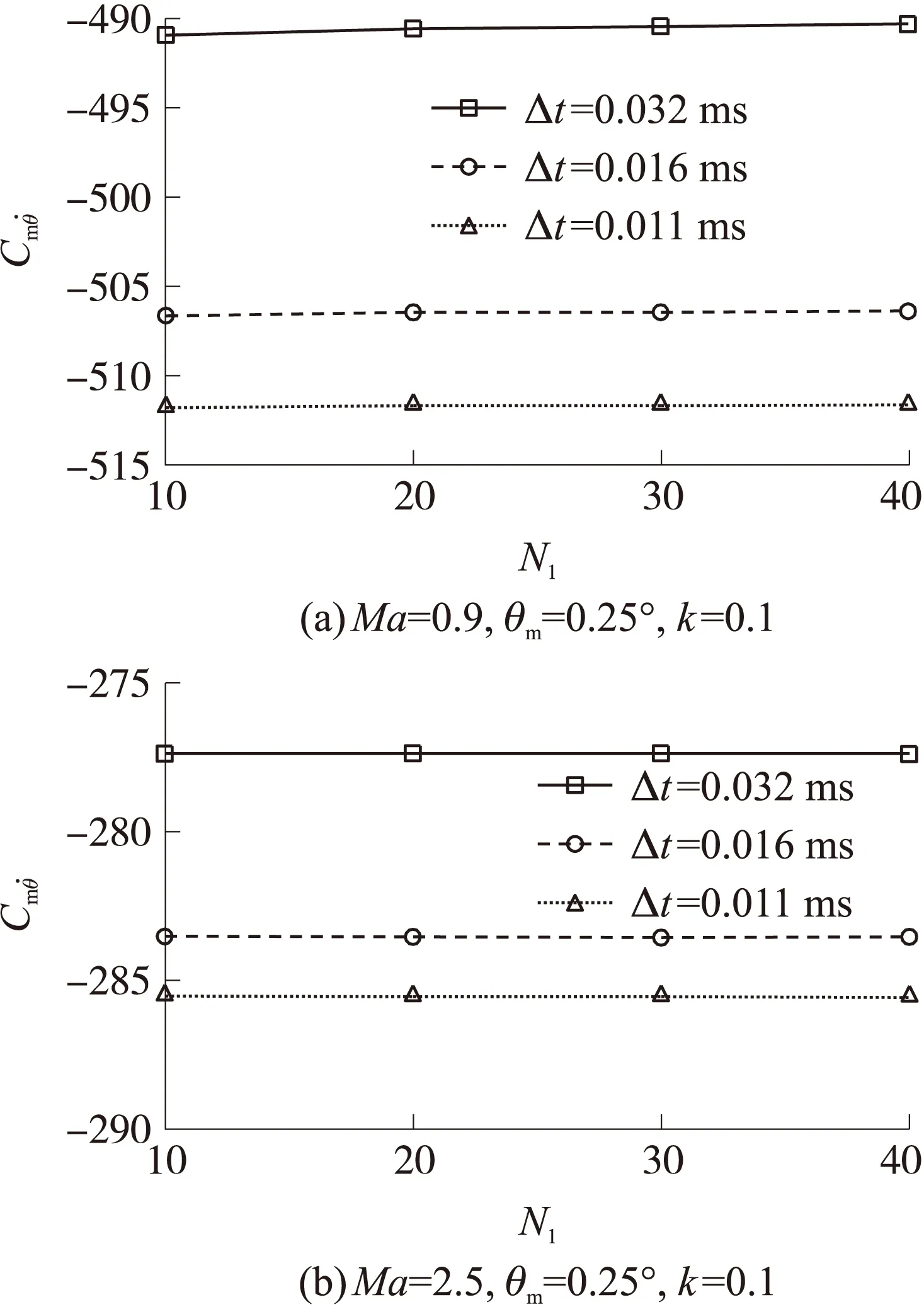
图6　不同时间步长和内迭代次数情况下的俯仰阻尼动导数

3.2强迫运动幅值与减缩频率的影响

图7给出了不同强迫运动幅值的俯仰力矩系数随攻角的变化结果,图8给出了不同强迫运动幅值和减缩频率的俯仰动导数计算结果。

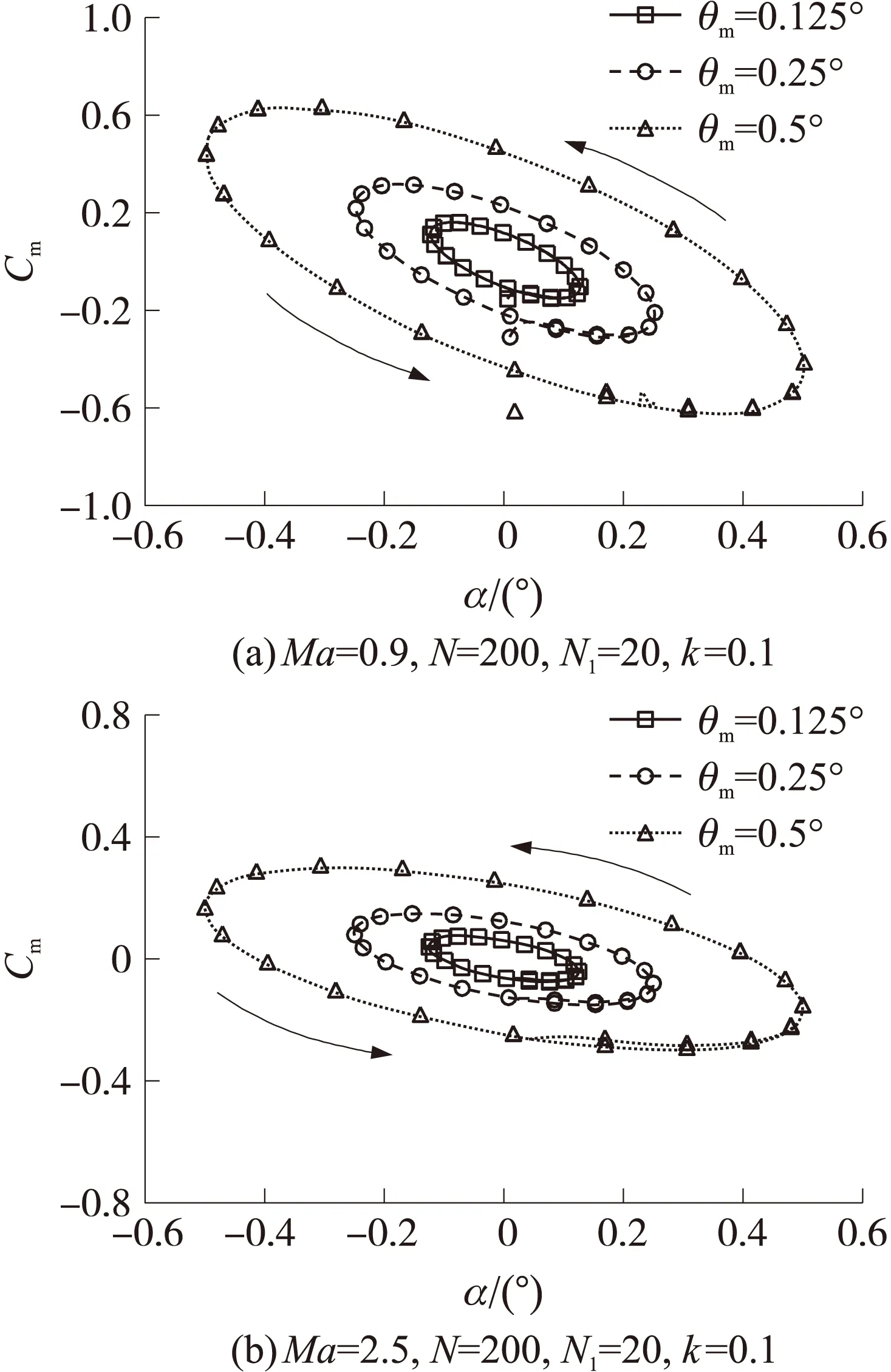
图7　不同强迫运动幅值情况下俯仰力矩系数随攻角的变化曲线

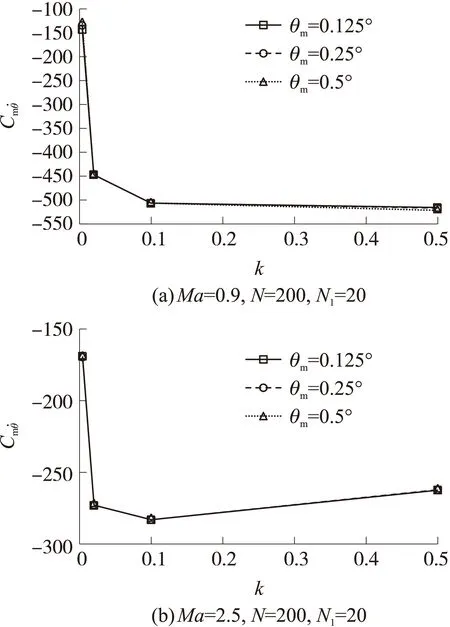
图8　不同运动幅值和减缩频率情况下的俯仰阻尼动导数

由图可知,强迫运动幅值越大,俯仰力矩系数越大。运动幅值对俯仰动导数计算结果影响很小,当时间步长和内迭代次数一定时,不同运动幅值对应的俯仰动导数数值计算结果很接近。减缩频率对动导数计算结果有着显著影响,当减缩频率超出某个范围时,动导数计算结果逐渐偏离实验值,计算精度迅速下降。其原因是减缩频率k很大时,式(3)略去与k2有关的高阶项会导致误差增大;减缩频率k很小时,非定常迟滞效应不能准确体现,也会导致误差增大。在实际计算时,应选择与实验减缩频率值相近的减缩频率进行动导数计算,才能保证计算结果与实验结果吻合较好。

4标模俯仰动导数计算结果与实验结果比较

采用上述方法,取N=200,NI=20,θm=0.25°,取k=0.01,对Ma=0.6,0.8,0.9,1.05,1.5,2.0,2.5,3.0条件下标模的动导数进行计算,CFD计算结果、实验结果[6]及文献[9]计算结果如图9所示。可知,计算结果精度较高,Ma≥1.5时,与实验结果相比最大相对误差不超过5%,与文献计算结果基本重合。0.9≤Ma<1.5时,实验结果存在较大的散布,本文计算结果与实验结果的平均值较为接近。Ma<0.9时,本文计算结果与实验结果吻合较好,优于文献[9]计算结果。

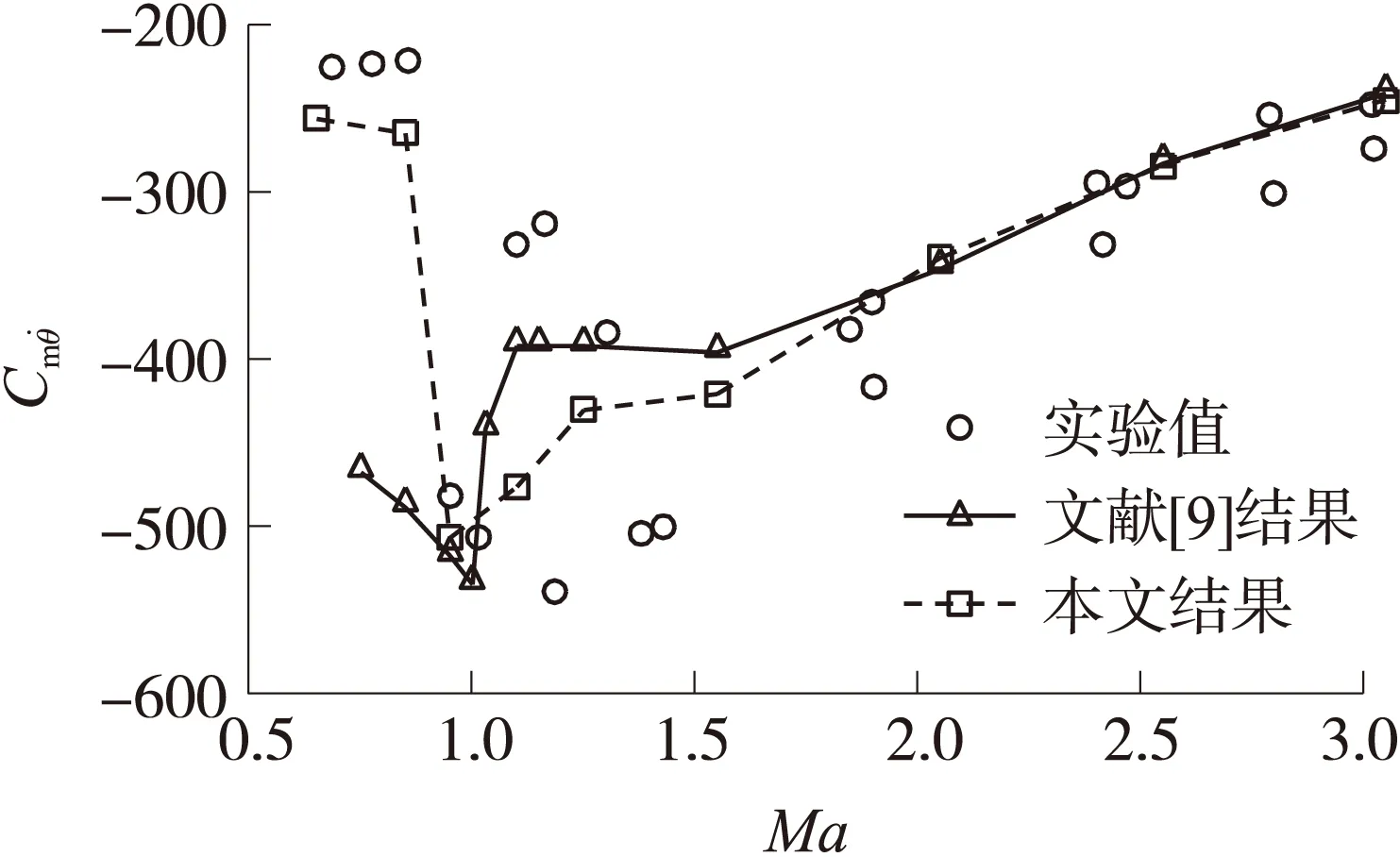
图9　俯仰阻尼动导数结果比较

5结束语

本文结合CFD技术对动导数数值计算方法进行了研究,讨论了时间步长、内迭代次数、强迫运动幅值、减缩频率对俯仰动导数计算结果的影响,计算了标模的俯仰动导数,与实验结果进行了比较。得到以下结论:

①时间步长与减缩频率是影响俯仰动导数计算结果的2个关键因素,应结合实验情况选择适当的时间步长和减缩频率进行计算,兼顾计算精度与计算效率。

②通过对标模的俯仰动导数进行计算,并与实验结果对比,可知本文采用的动导数数值计算方法能够得到较为精确的计算结果,能够满足型号研制的需求。

参考文献

[1]袁先旭,张涵信.基于CFD方法的俯仰静/动导数数值计算[J].空气动力学学报,2005,23(4):458-463.

YUAN Xian-xu,ZHANG Han-xin.The pitching satic/dynamic derivatives computation based on CFD method[J].Acta Aerodynamics Sinica,2005,23(4):458-463.(in Chinese)

[2]孙涛,高正红.基于CFD的动导数计算与减缩频率影响分析[J].飞行力学,2011,29(4):15-18.

SUN Tao,GAO Zheng-hong.Identify of aircraft dynamic derivatives based on CFD technology and analysis of reduce frequency[J].Flight Dynamics,2011,29(4):15-18.(in Chinese)

[3]刘绪.高超声速内外流一体化飞行器动态特性研究[D].长沙:国防科学技术大学,2011:14-17.

LIU Xu.Investigation of dynamic characteristics of hypersonic airframe/propulsion integrative vehicle[D].Changsha:National University of Defense Technology,2011:14-17.(in Chinese)

[4]卢学成.超音速、高超音速飞行器动导数高效的计算方法[J].航空计算技术,2008,38(3):28-31.

LU Xue-cheng.A high efficient method for computing dynamic derivatives of supersonic/hypersonic aircraft[J].Aeronautical Computing Technique,2008,38(3):28-31.(in Chinese)

[5]DESPIRITO J,SILTON S I,WEINACHT P.Navier-Stokes predictions of dynamic stability derivatives evaluation of steady-state methods[J].Journal of Spacecraft and Rockets,2009,46(6):1-13.

[6]VISUAL A B,JUBARAJ S.Numerical prediction of pitch damping stability derivatives for finned projectiles,AIAA 2011-0328[R].2011.

[7]Arnold Engineering Development Center.Experimental roll-damping,mangus,and static-stability characterictics of two slender missile configurations at high angles of attack(0 to 90 Deg)and Mach numbers 0.2 to 2.5,AD-A027[R].1976.

[8]DUPUIS A D,HATHAWAY W.Aeroballistic range and wind tunnel tests of the basic finner reference projectile from subsonic to high supersonic velocities,TM 2002-136[R].2002.

[9]JUBARAJ S.Numerical computations of dynamic derivatives of a finned projectile using a time-accurate CFD method,AIAA 2007-6581[R].2007

Calculation Method of Pitching Dynamic Derivatives Based on Unsteady CFD Technology

WU Bin,LU Yun,ZHOU Zhi-chao,FU Jian-ming

(Shanghai Electro-mechanical Engineering Institute,Shanghai 201100,China)

Abstract:Based on solving N-S equations,the numerical prediction method of pitching dynamic derivatives was studied.The effects of transient time-step,inner iterations,forced sinusoidal motion amplitude and reduced frequency on the calculation result of pitching dynamic derivatives were analyzed.Prediction of dynamic derivatives was conducted for the standard model of dynamic derivatives.The result shows that the transient time-step and reduced frequency are the most important factor affecting dynamic derivatives prediction.The general principle of choosing transient time-step and reduced frequency was presented.The calculation method of pitching dynamic derivatives based on unsteady CFD has high accuracy,and the result accords with the experiment data.The method has practical value.

Key words:pitching dynamic derivative;time step;inner iteration;forced sinusoidal motion amplitude;reduced frequency

收稿日期:2016-03-25

作者简介:伍彬(1987- ),男,工程师,研究方向为气动设计与分析。E-mail:wubin_no8@qq.com。

中图分类号:V211.3

文献标识码:A

文章编号:1004-499X(2016)02-0042-05