考虑J2摄动的弹道导弹高精度弹道预报和误差传播分析

孙　瑜,吴　楠,孟凡坤,邓启正

(1.中国人民解放军96669部队,北京 102208;2.信息工程大学 导航与空天目标工程学院,郑州 450001)



考虑J2摄动的弹道导弹高精度弹道预报和误差传播分析

孙瑜1,2,吴楠2,孟凡坤2,邓启正1

(1.中国人民解放军96669部队,北京 102208;2.信息工程大学 导航与空天目标工程学院,郑州 450001)

摘要:为进行高精度的弹道导弹弹道预报和误差传播分析,分析了平根数法解摄动方程的解形式,提出了一种考虑J2摄动并包含短周期项的解析法,并将其用于弹道预报,结合无迹变换构造了弹道预报的误差传播分析方法,解决了解析法中开普勒根数求解过程不可微、偏导数矩阵难以计算的问题。仿真结果表明,将解析法用于弹道预报时,J2摄动短周期项导致的误差达3个数量级,不可忽略;该算法预报的相对误差只有不到5%,精度与高精度数值法相当,远高于传统解析法,但运算速度是后者的7倍,具有更好的效费比。

关键词:弹道预报;无迹变换;J2摄动;解析法;短周期项

弹道预报与误差传播分析是战略预警系统的重要研究内容。传统的弹道预报方法通常有数值法和解析法两类。数值法是在充分考虑导弹飞行过程中各种摄动因素的基础上,建立导弹动力学方程,并采用一定的积分准则,利用数值逼近的方法计算弹道。文献[1～2]基于导弹动力学方程采用不同的数值积分方法计算弹道,验证了数值法的有效性。然而,这种方法预报的精确程度及计算速度与积分步长的选取有很大关系。小步长积分可以保证较高的预报精度,但是计算速度较慢;大步长积分计算速度快,但是预报精度不高。解析法是将导弹自由段飞行轨迹近似为椭圆弹道,通过计算开普勒根数进行弹道预报[3]。文献[4～7]基于椭圆弹道理论,采用解析法实现弹道预报,并分别从时间和预报精度等方面提出优化算法。尽管采用了优化算法,但解析法的精度仍低于数值法,这是因为解析法将地球视作质点,没有考虑地球是形状不规则的扁球体。文献[8～10]用考虑J2摄动的解析法计算人造卫星的轨道,因为人造卫星的运行周期很长,所以在解摄动方程的时候为了计算简便,通常忽略短周期项。然而导弹与人造卫星截然不同的是导弹的飞行时间很短,它的短周期项能否忽略值得讨论。

本文提出了一种考虑J2摄动并包含短周期项的解析法,并将其用于弹道预报,与数值法弹道预报进行仿真对比预报的精度及耗时。同时,在误差传播分析过程中,结合无迹变换(Unscented Transformation,UT)构造了弹道预报的误差传播分析方法,解决了解析法中开普勒根数求解过程不可微、偏导数矩阵难以计算的问题。

1考虑J2摄动并包含短周期项的弹道预报解析法

弹道导弹关机后进入自由段依靠惯性飞行,而自由段的高度一般在200 km以上,此时空气阻力的影响可以忽略不计,导弹主要外力源为地球中心引力,可以将导弹绕地球的运动视为二体运动,从理论上可以认为其弹道为椭圆弹道,落点为椭圆弹道与地球的交点。解析法通过计算椭圆弹道的6个开普勒根数来预报导弹任意时刻的状态。然而地球作为一个形状不规则的扁球体,其重力场对自由段的影响很大,二阶带谐系数J2对弹道导弹自由段落点偏差的影响最大可达十几km,四阶带谐系数J4对自由段落点偏差的影响可达数十m[11-12]。文献[13]采用数值积分法，分析了不同积分步长、不同纬度和发射方位角下J2和J4项以及不同阶数的扰动重力对导弹自由段落点的影响。J2项导致的摄动加速度约为10-3量级,而J4项摄动与大气阻力、第三体引力、太阳光压等其他摄动均为10-6量级及以下。若考虑J4项摄动,则大气阻力、三体引力、太阳光压等摄动均不能忽略,此时将大幅增加计算耗时。因此,综合考虑预报的精度和耗时,本文只考虑J2项摄动的影响。

1.1J2摄动运动方程

地球是一个形状不规则的扁球体,要精确地积分计算出其势函数,必须知道地球的表面形状及内部的密度分布。目前,通常采用球函数展开式推导出地球势函数的标准表达式[14]:

(Cnmcosmλ+Snmsinmλ)Pnm(sinφ)

(1)

式中:f为万有引力常数;me为地球质量;r为地球外地心距;ae为地球赤道平均半径;Jn为带谐系数,Jn=-Cn0;n≠m时,Cnm,Snm称为田谐系数;n=m时,Cnm,Snm称为扇谐系数;Pn(sinφ)称为勒让德函数;Pnm(sinφ)称为缔合勒让德函数;φ,λ为地球的地心纬度和经度。

物体绕地球运动的微分方程可写成:

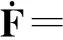
(2)

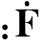
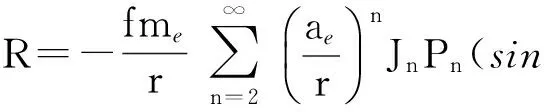
(Cnmcosmλ+Snmsinmλ)Pnm(sinφ)

(3)

当n=2时,即为考虑J2项摄动,取J2=1.082 63×10-3。

以6个开普勒根数为基本变量的拉格朗日型摄动运动方程[15]为

(4)

式中:a为轨道半长轴;e为偏心率;i为轨道倾角;Ω为升交点赤经;A为近地点幅角;M为平近点角;ω为平均角速度。设σ=(aeiΩAM)为开普勒根数构成的向量。

角析法中,平均根数法解摄动运动方程的特征是将摄动变化中不同性质的项区分开,相应的幂级数解的形式为

(5)

式中:

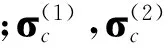
1.2开普勒根数转移

对于卫星而言,由于其在轨运行时间长,在计算其摄动运动方程时,为了计算简便通常忽略短周期项。对于弹道导弹,其飞行时间很短,所以在计算弹道导弹的摄动运动方程的时候不能忽略短周期项。而对于具体取到多少阶的摄动解,则要取决于预报的精度需求。文献[13]分析了不同阶数对弹道导弹自由段落点的影响,中低阶部分的影响从几十m到数百m不等,对于自由段射程约6 000km的弹道导弹,考虑到30阶左右可以达到m级的计算精度。本文重点在于综合考虑预报的精度和预警时间,因此本文只考虑一阶摄动解:包括所有的一阶摄动项(长期项、长周期项和短周期项)和二阶长期项。

考虑J2项摄动的平均根数法一阶解完整结果如下:

(6)

2基于无迹变换的误差传播分析

计算协方差矩阵时,纯粹的解析法需要计算笛卡尔坐标对开普勒根数的偏导数矩阵以及开普勒根数的转移矩阵,然而在计算开普勒根数转移矩阵时会出现一个问题:如果考虑短周期项,则开普勒根数求解过程不可微,偏导数矩阵难以计算;如果不考虑短周期项,计算转移矩阵所用的模型就与状态方程中所用的模型不一致,得到的解是完全错误的,这个结论在文献[16]中得到证实。而UT用采样点来近似状态向量的后验概率密度,结合UT的解析法在对弹道导弹进行误差传播分析时,就不需要计算笛卡尔坐标对开普勒根数的偏导数矩阵以及开普勒根数的转移矩阵。

(7)

(8)

通过椭圆弹道理论计算每个χ点对应的开普勒根数σ,然后考虑J2摄动采用平根数法解拉格朗日摄动运动方程,计算出t时刻对应的开普勒根数σt。通过这些非线性变换得到样点的输出:

Ψj=f(χj)j=0,1,…,12

(9)

最后,计算t时刻位置速度的均值和协方差矩阵:

(10)

基于UT变换来处理协方差矩阵的非线性传递,可以避开计算笛卡尔坐标对开普勒根数的偏导数矩阵以及开普勒根数的转移矩阵,并且对任意t时刻的协方差矩阵可以直接计算,不需要计算t时刻之前的协方差矩阵,能够有效提高弹道预报效率。

图1　系统流程框图

3仿真分析

仿真将通过普通解析法、基于UT的解析法和数值法对弹道导弹自由段进行预报,忽略空气阻力等其他摄动力,只考虑J2摄动的影响。普通解析法是直接解算摄动运动方程,通过计算开普勒根数变化率,解算出预报终点的位置速度;基于UT的解析法即上文所提的方法;数值法是通过对目标的运动方程进行积分计算弹道的方法,数值积分采用四阶龙格-库塔算法,仿真步长设为1s。首先分析解析法中短周期项对弹道预报的影响,然后分析基于UT的解析法计算的协方差矩阵和普通解析法进行蒙特卡洛仿真得到的均方根误差的一致性,最后对比分析解析法和数值法的预报精度和运算速度。设在地心惯性坐标系下,探测到导弹在自由段500s时刻的位置为x=2 163 451m,y=-6 342 006m,z=2 191 877m,速度vx=594.31m/s,vy=711.49m/s,vz=5 453.41m/s,协方差为

预报终点t=1 287s。

3.1短周期项对弹道预报的影响

有短周期项的解析法与数值法的均值差变化情况及无短周期项的解析法与数值法的均值变化情况如图2所示。

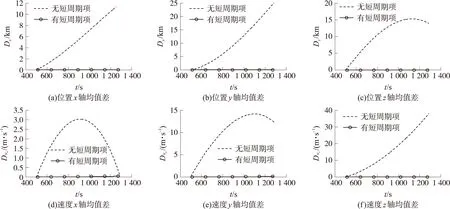
图2　均值之差的变化情况

从图2中可以看到,无短周期项的解析法与数值法计算的均值差在位置的x轴、y轴方向及速度的z轴方向均成发散趋势,速度的x轴、y轴方向及位置的z轴方向有成周期变化的趋势。位置的x轴方向终点处偏差约12km,y轴方向终点处偏差达到25km,z轴方向偏差最大达到15km,终点处约14km;速度的x轴方向偏差最大有3m/s,终点处为0.12m/s,y轴方向偏差最大达到14m/s,终点处为12.38m/s,z轴方向终点处偏差为38.08m/s。而与无短周期项相比,考虑了短周期项的解析法与数值法之差则小得多,接近于0。t=1 287s时刻,均值差的具体结果如表1所示。由此可见,由于弹道导弹飞行时间短,短周期项对弹道预报的影响很大,位置偏差能够达到3个数量级,所以在进行高精度弹道预报时不能忽略短周期项。

表1　均值之差仿真结果

3.2误差一致性分析

采用UT变换解析法计算的标准差和普通解析法1 000次蒙特卡洛仿真得到的均方根误差的变化情况如图3所示。

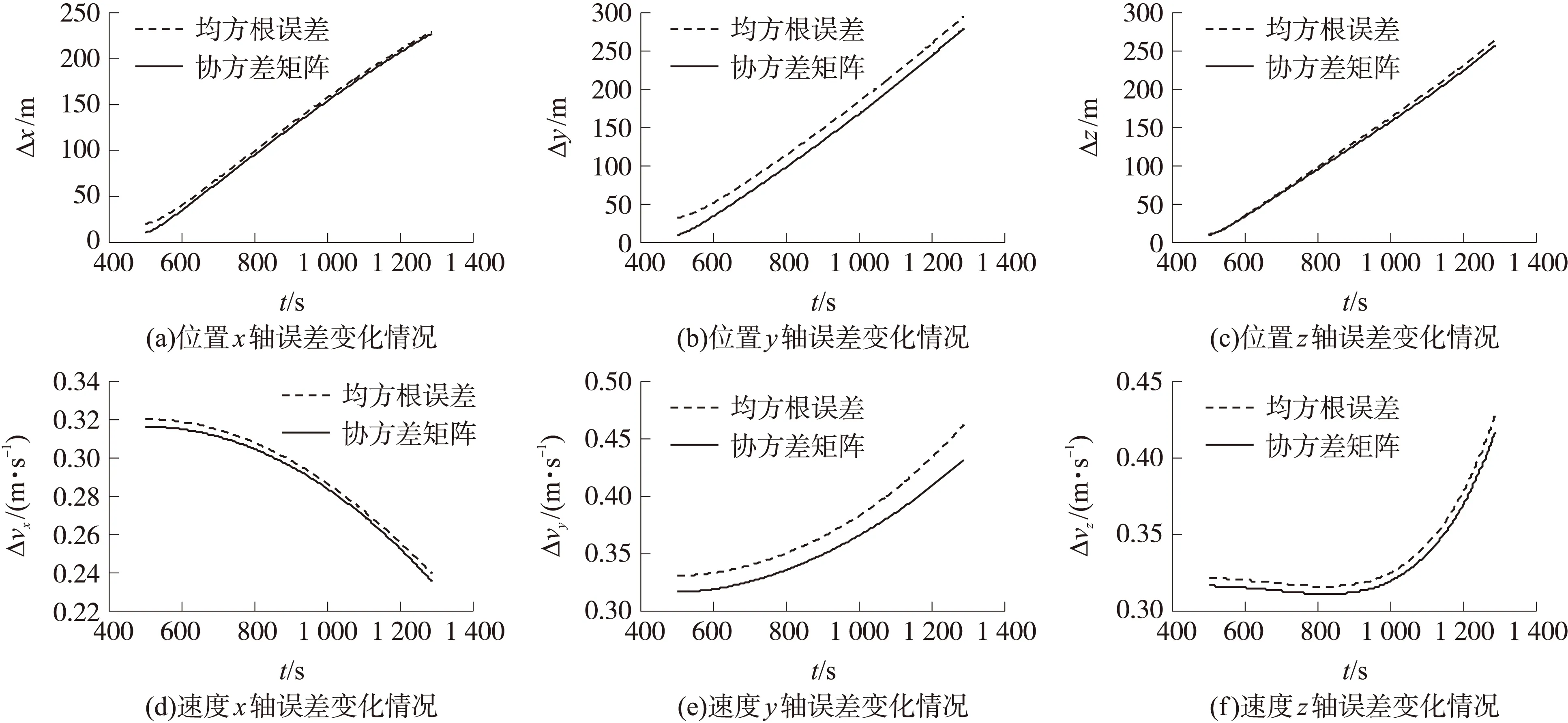
图3　普通解析法均方根误差与基于UT变换解析法的标准差变化情况

从图3中可以看到,二者的趋势基本相同,且预报的协方差位置和速度均略小于均方根误差。在预报的终点处,位置x轴的相对误差为1%,位置y轴的相对误差为5.7%,位置z轴的相对误差为3.03%,速度x轴的相对误差为1.7%,速度y轴的相对误差为7.1%,速度z轴的相对误差为2.6%。可见,二者的相对误差非常小,而UT变换计算的协方差矩阵比蒙特卡洛仿真计算的均方根误差略小,是因为协方差矩阵是截断误差,忽略了高阶项,属于正常误差,可以说二者是一致的。

3.3弹道预报和误差传播分析

图4给出了考虑J2摄动解析法的标准差和数值法1 000次蒙特卡洛仿真得到的均方根误差的变化情况。从图中可以看到,二者的变化趋势基本一致,解析法的协方差矩阵在x轴、y轴方向的位置和速度均略大于数值法的均方根误差,在z轴方向的位置和速度均略小于数值法的均方根误差,说明解析法的精度在x轴和y轴略低于数值法,而z轴略高于数值法。在预报的终点处,位置x轴的相对误差为4.6%,位置y轴的相对误差为4.2%,位置z轴的相对误差为2.5%,速度x轴的相对误差为4.8%,速度y轴的相对误差为3.5%,速度z轴的相对误差为1.1%。无论位置还是速度,两种方法的相对误差都不超过5%,说明解析法和数值法的预报精度相当,基本在同一数量级。

考虑J2摄动的解析法的总耗时为128.075ms,其中每个χ点的总耗时为9.851ms。每个χ点在传播的过程中,500s初始时刻的位置速度转换成开普勒根数的耗时最大,为4.478ms,占其传播总耗时的45%左右;计算500s时刻平均根数的耗时为2.001ms,占20%左右;计算长期项耗时为0.883ms,占9%左右;计算1 287s时刻的平均根数的耗时为0.616ms,占6%左右;计算短周期项和长周期项的耗时分别为0.755ms和0.698ms,分别占8%和7%左右。可见,在解析法中位置速度与开普勒根数之间的转换耗时最大。数值法积分步长为1s,每步长的平均耗时约为1.048ms,预报自由段时长为788s,数值法总耗时为826.602ms,是解析法的7倍左右。

预报飞行时长800s左右的弹道得到相同级别的精度,数值法计算耗时可以达到考虑J2摄动解析法的7倍左右。原因是数值法在计算任意时刻导弹状态的时候,需要按照一定的步长逐步积分,耗时与所选取的步长成反比,保证一定的精度就需要选取较小的步长,而以耗时的增加为代价;而解析法中,在观测到导弹初始状态后,就能够快速计算出弹道6个开普勒根数的变化情况,只要给出任意时刻点,就可以直接计算导弹在该时刻的状态,所以计算速度快。

图4　数值法均方根误差与考虑J2摄动解析法标准差的变化情况

综上所述,总结得到如下结论:

①由于弹道导弹飞行时间短,短周期项对弹道预报影响很大,位置偏差能够达到3个数量级,在进行高精度弹道预报的时候不能忽略;

②结合UT的解析法进行误差传播分析,能够有效避开计算笛卡尔坐标对开普勒根数的偏导数矩阵以及开普勒根数的转移矩阵;

③考虑J2摄动的解析法与积分步长为1s的数值法相比,弹道预报的精度在同一数量级,并且在预报800s左右的弹道时,耗时只有数值法的1/7左右。

4结束语

本文通过仿真对解析法和数值法在弹道预报中的性能进行了对比分析。解析法在进行误差传播分析时结合UT,能够有效避开计算笛卡尔坐标对开普勒根数的偏导数矩阵以及开普勒根数的转移矩阵。传统的解析法只是简单地近似成二体问题,没有考虑其他摄动因素,所以计算精度不高;而考虑了J2摄动之后的解析法,计算精度和误差传播发散程度都与积分步长为1s的数值法相当,在预报800s左右的弹道时运算速度是数值法的7倍左右。但是考虑J2摄动的解析法在弹道预报中,不能够像计算卫星轨道一样简单地忽略短周期项,短周期项对弹道预报影响很大,在进行高精度的预报弹道时不能忽略。

参考文献

[1]张龙杰,谢晓方.通用变步长弹道仿真方法研究[J].弹道学报,2011,23(2):42-46.

ZHANG Long-jie,XIE Xiao-fang.Research on general variable step-size ballistic simulation method[J].Journal of Ballistics,2011,23(2):42-46.(in Chinese)

[2]程诚,张小兵.某制导炮弹二位两相流内弹道性能分析与数值模拟研究[J].兵工学报,2015,36(1):58-63.

CHENG Cheng,ZHANG Xiao-bing.Two-dimensional numerical simulation on two-phase flow interior ballistic performance of a guided projectile[J].Acta Armamentarii,2015,36(1):58-63.(in Chinese)

[3]张毅,杨慧耀,李俊莉.弹道导弹弹道学[M].长沙:国防科技大学出版社,1999.

ZHANG Yi,YANG Hui-yao,LI Jun-li.Ballistic missile ballistics[M].Changsha:National University of Defense Technology Press,1999.(in Chinese)

[4]李森,刘红军,程仲.提高弹道导弹落点预报精度方法[J].电子科技,2012,25(9):85-87.

LI Sen,LIU Hong-jun,CHENG Zhong.Improvement of TBM’s impact-point prediction precision[J].Electronic Sci & Tech,2012,25(9):85-87.(in Chinese)

[5]沈慧娜,徐振来.提高弹道导弹落点预报精度的动弧平滑平均法[J].现代雷达,2009,31(7):55-58.

SHEN Hui-na,XU Zhen-lai.Moving arc smoothing averaging algorithm for improving the prediction precision of ballistic missile impact point[J].Modern Radar,2009,31(7):55-58.(in Chinese)

[6]刘仁,王爱华,郭桂治.基于关机点状态的战术弹道导弹落点估计[J].空军工程大学学报,2010,11(1):27-30.

LIU Ren,WANG Ai-hua,GUO Gui-zhi.Impact point estimation of tactical ballistic missile based on the state of burnout point[J].Journal of Air Force Engineering University,2010,11(1):27-30.(in Chinese)

[7]刘彦君,乔士东,黄金才,等.一种高精度弹道导弹落点预测方法[J].弹道学报,2012,24(1):23-26.

LIU Yan-jun,QIAO Shi-dong,HUANG Jin-cai,et al.A method of impact point prediction of ballistic missile[J].Journal of Ballistics,2012,24(1):23-26.(in Chinese)

[8]刘林.一种人造地球卫星的摄动计算方法[J].天文学报,1975,16(1):5-80.

LIU Lin.A calculating method of perturbation of artificial satellite[J].Acta Astronomica Sinica,1975,16(1):5-80.(in Chinese)

[9]曹文华,李传荣,李子扬,等.基于摄动模型的卫星轨道预测算法精度评估[J].遥感信息,2012,27(6):21-27.

CAO Wen-hua,LI Chuan-rong,LI Zi-yang,et al.Accuracy assessment of satellite orbit prediction based onJ2perturbation model[J].Remote Sensing Information,2012,27(6):21-27.(in Chinese)

[10]张俊.基于开普勒二体运动修正地球扁率J2摄动项算法[J].航天控制,2014,32(6):22-25.

ZHANG Jun.Correction algorithm ofJ2perturbations of the earth oblateness based on Kepler two-body motion[J].Aerospace Control,2014,32(6):22-25.(in Chinese)

[11]郑伟,汤国建.上升段引力常数变化及其对弹道导弹运动的影响[J].导弹与航天运载技术,2008,295(3):12-14.

ZHENG Wei,TANG Guo-jian.Gravitation constant variety in ascend phase and its effect on ballistic missile[J].Missile and Space Vehcile,2008,295(3):12-14.(in Chinese)

[12]郑伟,汤国建.弹道导弹自由段解算的等高约束解析解[J].宇航学报,2007,28(2):269-272.

ZHENG Wei,TANG Guo-jian.Contour restricted analytical solution for free flight trajectory of ballistic missile[J].Journal of Astronautics,2007,28(2):269-272.(in Chinese)

[13]冯伟,刘根友,郝晓光.重力场对弹道导弹自由段落点影响的仿真分析[J].测绘科学,2009,34(5):118-120.

FENG Wei,LIU Gen-you,HAO Xiao-guang.Simulated analysis of the effect of gravity field to the fall point in free flight trajectory of ballistic missile[J],Science of Surveying and Mapping,2009,34(5):118-120.(in Chinese)

[14]贾沛然,陈克俊,何力.远程火箭弹道学[M].长沙:国防科技大学出版社,1993.

JIA Pei-ran,CHEN Ke-jun,HE Li.Long-range rocket ballistics[M].Changsha:National University of Defense Technology Press,1993.(in Chinese)

[15]李济生,叶杰,王家松,等.航天器轨道确定[M].北京:国防工业出版社,2003.

LI Ji-sheng,YE Jie,WANG Jia-song,et al.Determination of spacecraft[M].Beijing:National Defense Industry Press,2003.(in Chinese)

[16]MAY J A.A study of the effects of state transition matrix approximations,NASA CP 21123[R].1980.

Analysis on High Precision Trajectory Prediction and Error Propagation of Ballistic Missile ConsideringJ2Perturbation

SUN Yu1,2,WU Nan2,MENG Fan-kun2,DENG Qi-zheng1

(1.Unit 96669 of PLA,Beijing 102208,China;2.College of Navigation and Aerospace Target,Information Engineering University,Zhengzhou 450001,China)

Abstract:To carry out high-precision trajectory prediction and error propagation analysis of ballistic missile,the solution form of mean element algorithms for perturbation equation was analyzed,and an analytical algorithm consideringJ2perturbation and containing the short period term was proposed for trajectory prediction.By constructing the error propagation analysis method of trajectory prediction based on unscented transform,the problem that the Kepler elements is not differentiable and the partial derivative matrix is difficult to calculate was solved.The simulation results show that the error caused by theJ2perturbation short period term,which can not be ignored,reaches 3 orders of magnitude when analytical algorithm is applied in the trajectory prediction.The relative error predicted by the proposed algorithm is only less than 5%,and the precision is far higher than the precision of traditional analytical algorithm,which is comparable with the precision of high-precision numerical algorithm,but the operation speed is 7 times of the latter,and the algorithm has a better effectiveness-cost ratio.

Key words:trajectory prediction;unscented transformation;J2perturbation;analytical algorithm;short-period term

收稿日期:2015-12-30

作者简介:孙瑜(1986- ),男,助理工程师,硕士,研究方向为空天目标预警信息处理。E-mail:woshizhongsy@163.com。

中图分类号:TJ760.1

文献标识码:A

文章编号:1004-499X(2016)02-0018-07