某导弹无依托发射场坪动态响应影响因素敏感度分析

杨春浩,马大为,王晓锋,朱忠领,仲健林

(南京理工大学 机械工程学院,南京 210094)



某导弹无依托发射场坪动态响应影响因素敏感度分析

杨春浩,马大为,王晓锋,朱忠领,仲健林

(南京理工大学 机械工程学院,南京 210094)

摘要:为了研究导弹无依托发射场坪动态响应的影响因素,基于最优拉丁超立方(OLHD)试验设计方法和径向基神经网络近似技术,建立了带有塑性损伤本构关系的无依托发射场坪的近似模型;对场坪位移动态响应的各影响因素进行了敏感度分析。研究结果表明:土基层的弹性模量、改性沥青混凝土层和水稳碎石层的厚度为场坪位移响应的主要影响因素,且与位移响应均呈反比关系;沥青混凝土材料的弹性模量在不同区间时对场坪位移响应的敏感度不同。

关键词:发射场坪;动态响应;近似模型;敏感度分析

无依托发射是指导弹发射不再依靠预设的发射场地而是随机选取场地发射,具有高机动性、高隐蔽性等优势,已逐渐成为陆基机动导弹的重要发展方向[1]。在导弹发射过程中,场坪处于大变形、高应变率等状态,其内部的拉压应力相互作用会使材料受到不同程度的破坏,影响发射平台稳定性和导弹发射精度。Ren J等[2]运用弹塑性理论对导弹发射阶段场坪动态响应进行了研究,结果表明场坪位移响应最大值位于弹射载荷作用的中心点,最大应力值位于弹射载荷作用边缘。周晓和等[3-4]对准发射阶段和发射阶段的场坪响应进行了研究,表明2个阶段场坪最大应力点均位于底基层与土基层的交界面处。张震东等[5]分析了沥青混凝土面层的冲击损伤,得到了场坪面层响应的变化规律和分布规律。我国公路修筑覆盖面广阔且错综复杂,需研究各类发射场坪在弹射载荷作用下的动态响应。目前,场坪响应研究方法主要为显式动态计算,建模难度大,机时消耗长,难以应对场坪快速高效计算的需求。

本文结合混凝土塑性损伤本构关系,建立了含场坪的发射平台数值模型;通过试验设计和径向基神经网络方法,形成场坪高效计算模型;对场坪动态响应的主要影响因素进行敏感度评估。

1含场坪的发射平台数值模型

本文对典型的沥青混凝土公路发射场坪进行研究。如图1所示,场坪数值模型从上至下依次为改性沥青混凝土、沥青混凝土Ⅰ、沥青混凝土Ⅱ、水稳碎石、石灰土级配碎石和土基,每层的厚度分别用H1,H2,H3,H4,H5,H6表示;每层材料的弹性模量分别用E1,E2,E3,E4,E5,E6表示。

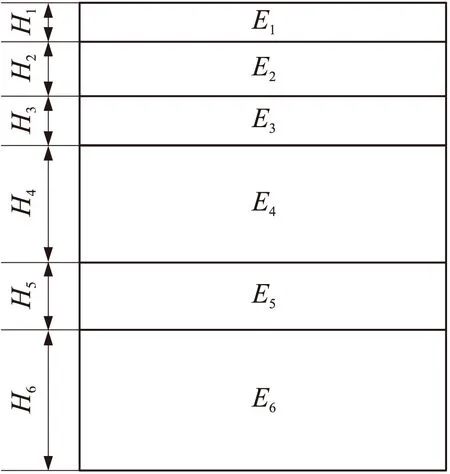
图1　无依托发射场坪结构示意图

非线性和随机性是混凝土受力行为的2个基本特征[6]。因此采用一般的线弹性模型难以准确计算场坪的响应。为提高发射过程中场坪动态响应的计算精度,兼顾计算效率,对发射场坪按如下方式建模:将重点研究的沥青混凝土材料设置为塑性损伤模型[7-8],其膨胀角为30°,偏心率为0.1,初始等效双轴抗压屈服应力与初始单轴抗压屈服应力的比值为1.16,受拉子午线与受压子午线常应力的比值为0.667,粘滞系数为0.000 5;其余各层材料是非主要研究对象,为提高计算效率,均以线弹性本构关系处理,各层初始弹性模量E、泊松比μ和密度ρ见表1[8];各层之间采用连续形式进行模拟,不考虑非连续层间的力学特性;各层四周均设置自由约束,土基底面设置为固定端约束。图2为场坪数值模型。

表1　发射场坪初始材料参数与结构参数

图2　场坪数值模型

在此基础上,建立含场坪的发射平台数值模型。发射平台主要由场坪、发射车、发射筒和导弹组成。发射车部分主要由车架、前弹托、轮胎、油气悬架、起竖油缸和前后液压支腿等组成。采用三铰点式起竖机构,支撑方式为纯支腿支撑,即只考虑前、后支腿刚性支撑盘及自适应底座与场坪的接触关系。图3为发射平台待发射状态示意图。

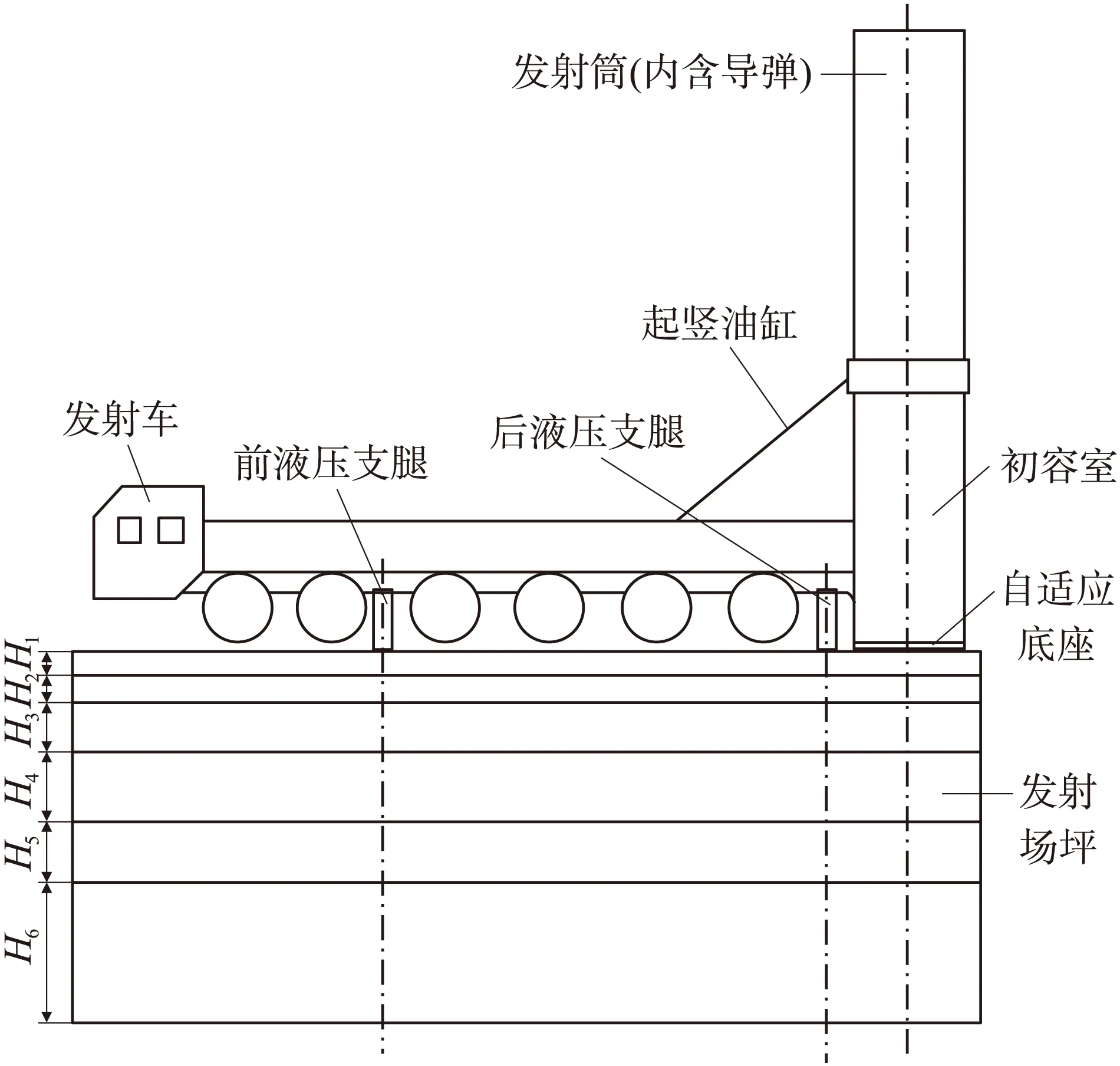
图3　含场坪的发射平台准发射状态示意图

由图3可知,在待发射状态,发射车自身的重力使得场坪受稳态载荷,为提高计算精度,先建立初始应力场。在此基础上对导弹发射过程进行动态仿真,重点关注场坪位移响应的峰值(在自适应底座处[4])。

2发射场坪近似模型的建立

近似模型是用一个简单的函数关系近似替代实际的复杂仿真模型,具有计算精度较高、消耗机时少等特点。本文在构建近似模型之前,首先采用优化拉丁超立方试验设计(OLHD)方法进行数据采样,以便在较小的计算代价下得到更为准确的近似模型。

2.1径向基神经网络方法

径向基神经网络(RBF)在逼近复杂函数,特别是非线性函数方面具有很强的能力[9-10]。其整体性能优于Kriging方法和响应面方法,且具有较强的容错功能。即使有“噪声”输入,也不会影响网络整体性能。

所谓径向基函数,是一种径向对称函数,对任意插值样本点X(a),可以描述为φ(‖X-X(a)‖),其中‖·‖为Euclidean范数,X为径向基函数的中心,a表示第a个样本,a=1,2,…,m。对于给定的样本点集(x1x2… xm)T,径向基函数模型为

(1)

式中:λa和βa为待定系数。径向基神经网络的神经元模型如图4所示,其节点激活函数即为径向基函数。

图4　径向基神经元模型

由图4可以看出,节点激活函数以输入向量和权值向量间的距离作为自变量,其一般表达式为

R(‖dist‖)=e-‖dist‖2

(2)

由此神经元搭建的径向基神经网络如图5所示。图中X=(x1x2… xm)T为网络输入矢量;vij为输入层到隐含层的连接权值;wij为隐含层到输出层的连接权值;隐含层节点数i=1,2,…,h;y=(y1y2… yn)T为网络输出。

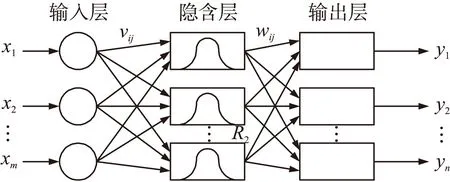
图5　径向基神经网络结构

径向基神经网络常用Gaussian函数,其激活函数可表示为

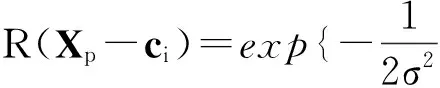
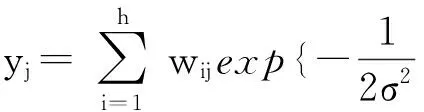
(4)

式中:yj为网络的第j个输出节点的时间输出。

2.2发射场坪近似模型

本文选取11个参数作为输入变量,包括场坪各层材料的弹性模量和除土基之外的其余5层材料的厚度。根据实际场坪中各层材料弹性模量和厚度的范围给出各设计参数的变化范围,见表2。

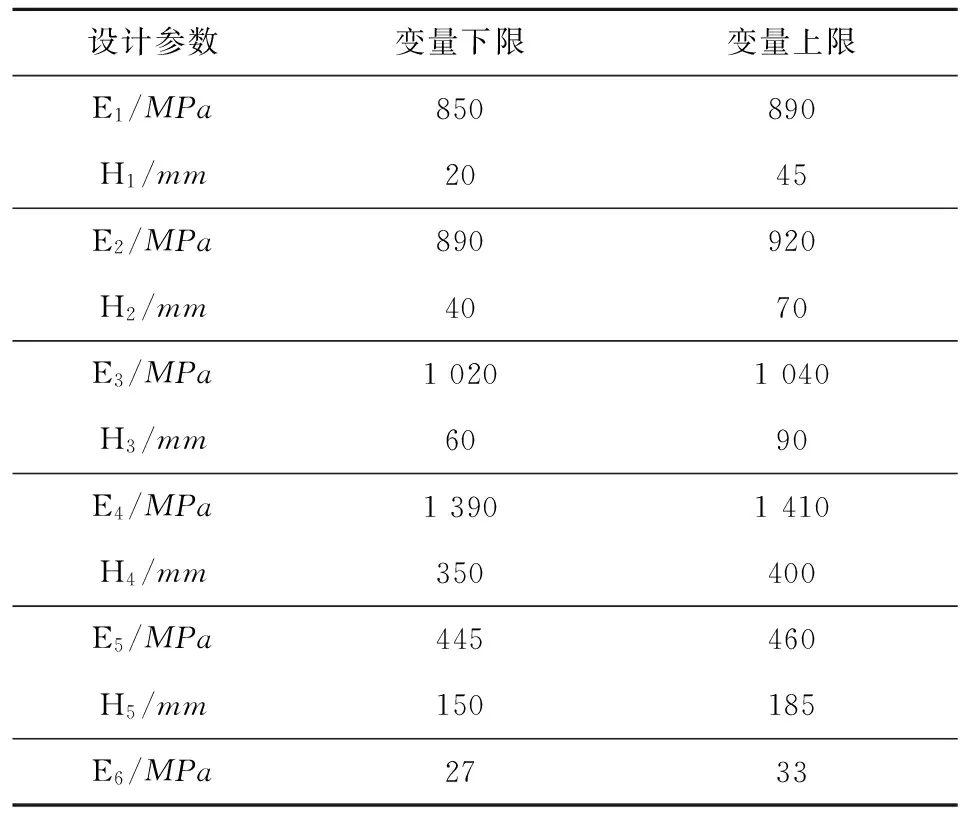
表2　输入变量变化范围及含义

在弹射过程中,场坪变形会导致发射平台稳定性减弱、导弹发射精度降低。因此,选取场坪位移响应峰值作为近似模型的输出参数。

为提高近似模型的准确性,同时考虑计算成本。本文选取100组数据样本点构建输入、输出参数之间的近似函数模型。建立模型的流程如图6所示。

图6　建立近似模型流程图

2.3近似模型验证

影响近似模型拟合精度和拟合效率的主要因素是变量个数和非线性特性,近似模型拟合精度检验的常用准则是相对均方根误差(r),定义为

(5)

如图7所示,随机抽取40组数据对近似模型进行误差分析。结果表明,近似模型计算结果D与数值计算结果D0最大相对误差为0.68%。

近似模型总方差的来源主要有近似模型本身以及拟合误差2个方面。方差分析采用离均差平方和s2,定义为

(6)

(7)

R2越接近1则拟合越精确。本文中近似模型的R2=0.96,接近于1,因此近似模型较为准确。

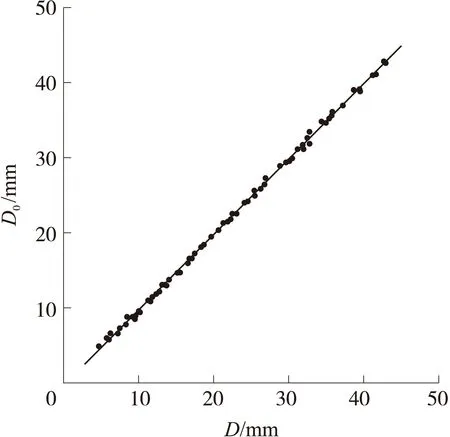
图7　近似模型误差分析

由以上误差和方差分析可以看出,通过径向基神经网络方法得到的发射场坪位移响应近似模型精度较高,在后续研究中可以采用此模型代替数值模型。

3发射场坪位移响应影响因素的敏感度分析

3.1场坪位移响应的主要影响因素

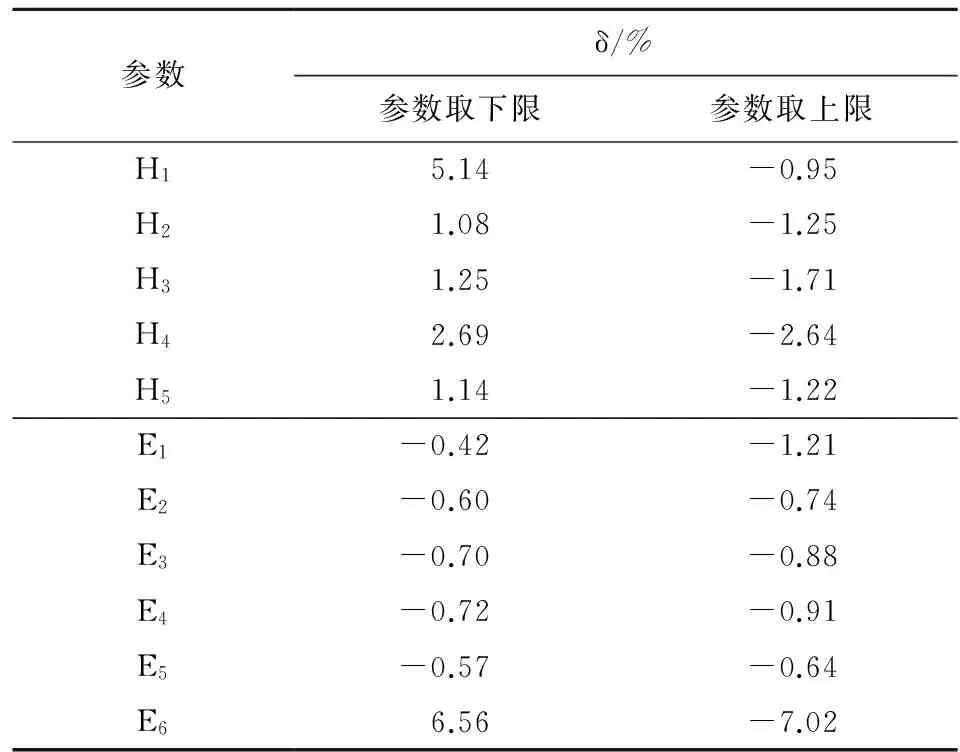
表3　发射场坪位移响应求解结果

由表3可以看出,当场坪位移响应的各影响因素取值从下限变化至上限时,E6,H1和H4对位移响应的影响最大,变化比例大于5%;其他参数对位移响应影响较小。E6,H1和H4为影响场坪位移响应的主要因素。

3.2主要影响因素敏感度分析

将3个主要影响因素按比例递增取值,并代入2.2节中建立的近似模型进行计算,得到相应的发射场坪位移响应变化比例S与主要影响因素变化比例T的关系,如图8所示。

图8　位移响应变化比例与主要影响因素变化比例的关系

由图8可见,3个参数与位移响应均呈反比关系。其原因在于:E6为土基的弹性模量,从宏观角度看则代表着土基的软硬程度,因此场坪位移响应随土基弹性模量降低而增大;H1和H4为场坪改性沥青混凝土层和水稳碎石层的厚度,随着厚度的增加,场坪位移响应减小。下面对3个主要因素的敏感度进行横向对比,如图9所示。

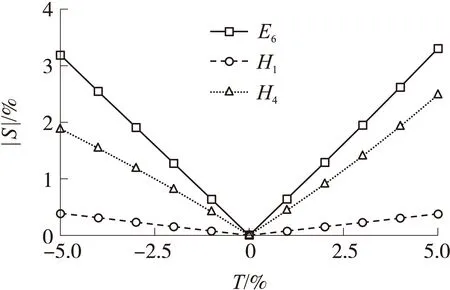
图9　主要影响因素敏感度分析

由图9可见,E6对场坪位移响应的影响最大,H1次之,H4则对其影响最小。其原因在于:在整个发射场坪模型中,土基材料的弹性模量E6远小于其他材料,在受到发射载荷作用时,土基的形变最大,即位移响应最大。H1,H4增大时,发射载荷的传递距离和影响半径均增大,传递到土基层的力减小、受力面积增大,因此场坪位移响应减小。3个主要因素对发射场坪位移响应影响的敏感度排序为E6>H1>H4。

3.3次要影响因素敏感度分析

通过3.2节中对各主要影响因素的深入分析可以得出结论,场坪各层的弹性模量和厚度均与位移响应呈反比关系。为进一步考察材料弹性模量和厚度对位移响应的敏感度,再选取E1、E4、H3和H54个参数进行次要因素的横向对比分析,如图10所示。可以看出:E4对场坪位移响应的影响最大,其次是E1,而H3和H5影响较小;其曲线趋势进一步验证了材料参数与场坪响应的反比关系。4个因素对场坪位移响应的敏感度排序为E4>E1>H5>H3。

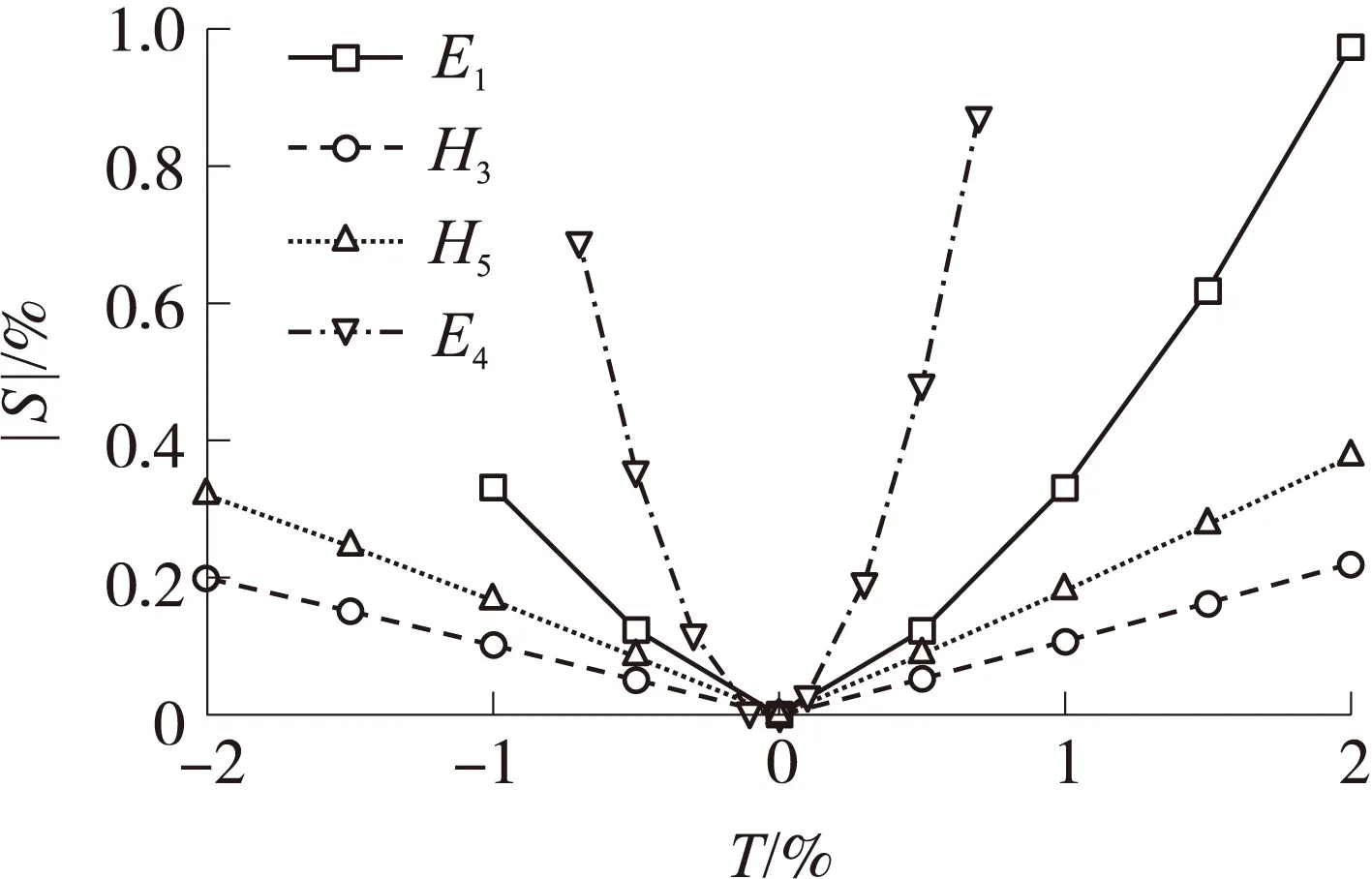
图10　次要影响因素敏感度分析

3.4沥青混凝土弹性模量敏感度分析

图11为E1与发射场坪位移响应变化S的关系。由于面层为塑性损伤模型,可以看出:在曲线前段,所受应力超过材料的屈服极限,材料产生塑性形变,E1与位移响应呈现明显的非线性关系。当材料弹性模量大于临界值(本文接近于884MPa)后,场坪所受应力没有达到材料的屈服极限,即材料只发生弹性形变,因此曲线后段表现为线性关系。

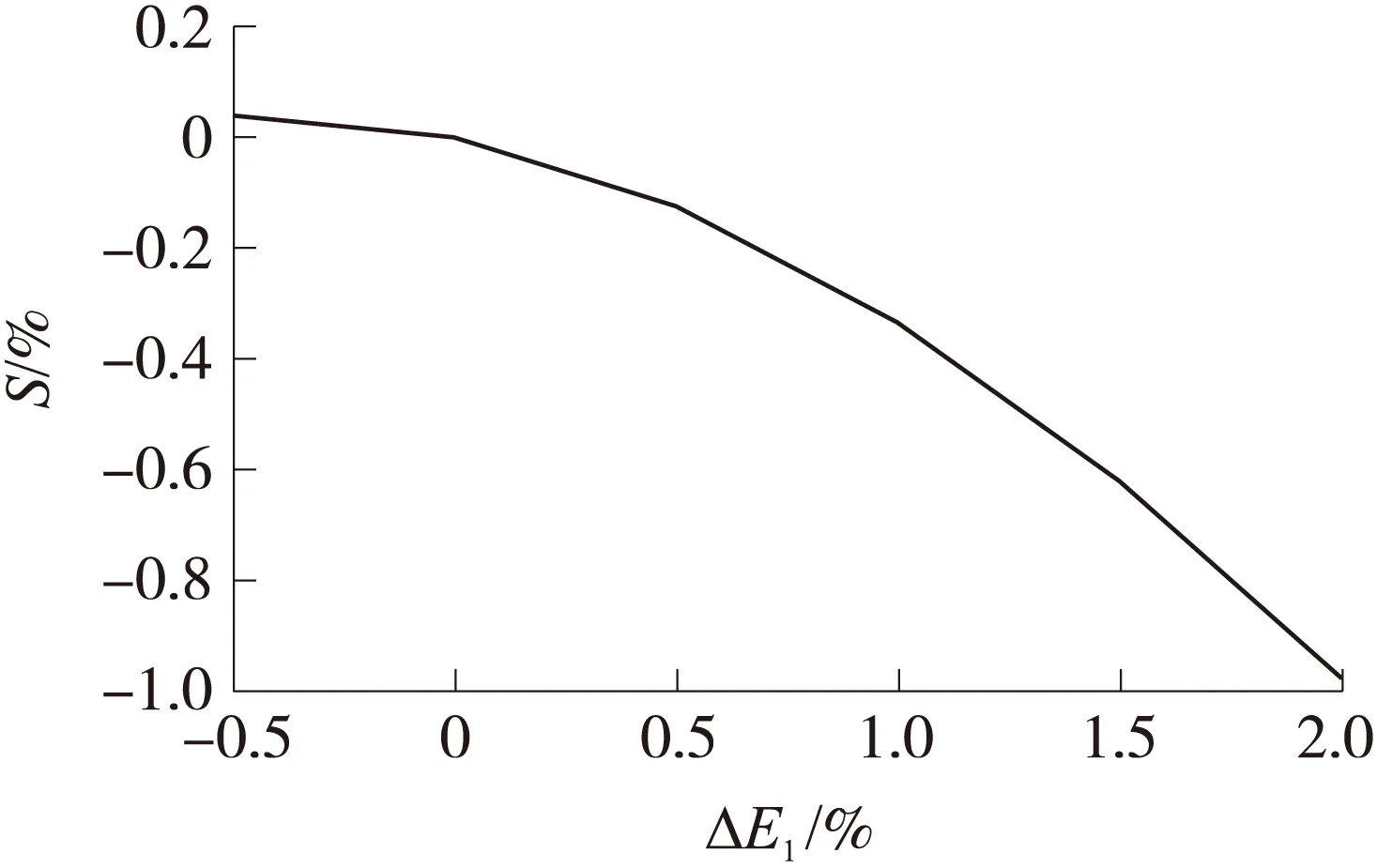
图11　面层弹性模量敏感度分析

4结论

通过对场坪位移动态响应的各影响因素进行敏感度分析,可以得到以下结论:

①场坪位移响应的近似模型解与数值解的最大相对误差约为0.68%,拟合精确度R2=0.96,因此近似模型是正确的。

②场坪各层材料的弹性模量及厚度均与位移响应呈反比关系。土基层的弹性模量E6、改性沥青混凝土层的厚度H1和水稳碎石层的厚度H4为场坪位移响应的主要影响因素,其敏感度排序为E6>H1>H4。

③在面层弹性模量E1较小时,材料发生塑性形变,呈非线性关系;当E1大于临界值后,材料仅产生弹性形变,E1与位移响应呈线性关系。

本文针对高效计算需求,建立了场坪近似模型,并研究了场坪动态响应影响因素的敏感度,为导弹无依托发射装备的设计与优化提供支撑。

参考文献

[1]SPEARMAN M L.Innovation in aerodynamic design features of soviet missiles,NASA 20080014230[R].2008.

[2]REN J,ZHOU X H,MA D W,et al.Study on elasto-plastic response of the unsupported random launching site for the missile[J].Advanced Materials Research,2014,945:1 274-1 279.

[3]周晓和,王惠方,马大为,等.导弹无依托待发射阶段场坪准静态响应研究[J].弹道学报,2015,27(2):91-96.

ZHOU Xiao-he,WANG Hui-fang,MA Da-wei,et al.Study on unsupported launching site quasi-static response during missile standby phase[J].Journal of Ballistics,2015,27(2):91-96.(in Chinese)

[4]周晓和,马大为,胡建国,等.某导弹无依托发射场坪动态响应研究[J].兵工学报,2014,35(10):1 595-1 603.

ZHOU Xiao-he,MA Da-wei,HU Jian-guo,et al.Research on dynamic response of launching site for missile unsupported random launch[J].Acta Armamentarii,2014,35(10):1 595-1 603.(in Chinese)

[5]张震东,马大为,胡建国,等.弹射冲击载荷作用下沥青混凝土路面面层损伤[J].工程力学,2015,32(10):161-168.

ZHANG Zhen-dong,MA Da-wei,HU Jian-guo,et al.Damage of surface layer of asphalf concrete pavement under launching impact load[J].Engineering Mechanics,2015,32(10):161-168.(in Chinese)

[6]李杰,吴建营,陈建兵.混凝土随机损伤力学[M].北京:科学出版社,2014.

LI Jie,WU Jian-ying,CHEN Jian-bing.Stochastic damage mechanics of concrete structures[M].Beijing:Science Press,2014.(in Chinese)

[7]江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005.

JIANG Jian-jing,LU Xin-zheng,YE Lie-ping.Finite element analysis of concrete structures[M].Beijing:Tsinghua University Press,2005.(in Chinese)

[8]王金昌,朱向荣.软土地基上含反射裂缝沥青道路的动力响应分析[J].中国公路学报,2004,17(1):1-6.

WANG Jin-chang,ZHU Xiang-rong.Dynamic analysis of asphalt concrete pavement on soft clay ground[J].China Journal of Highway and Transport,2004,17(1):1-6.(in Chinese)

[9]王雷.防空火箭炮系统发射动力学研究[D].南京:南京理工大学,2012.

WANG Lei.Study of launching dynamics for antiaircraft rocket launcher system[D].Nanjing:Nanjing University of Science & Technology,2012.(in Chinese)

[10]方开泰,马长兴.正交与均匀试验设计[M].北京:科学出版社,2001.

FANG Kai-tai,MA Chang-xing.Orthogonal and uniform design[M].Beijing:Science Press,2001.(in Chinese)

Sensitivity Analysis of Factors Affecting Launching-site Dynamic Response of Missile With Unsupported Random Launch

YANG Chun-hao,MA Da-wei,WANG Xiao-feng,ZHU Zhong-ling,ZHONG Jian-lin

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

Abstract:The purpose is to study the factors affecting launching-site dynamic-response of missile with unsupported random launch.Based on the optimal-Latin-hypercube-design(OLHD)test design method and RBF neural network approximation technique,the approximate model was established,which included the plastic damage constitutive relation of unsupported-random-launch launching-site.Using this model,the sensitivity research for effect factors of the launching site displacement dynamic-response was conducted.The results show that:the elastic modulus of soil lay,the thickness of modified bituminous concrete lay and cement stabilized macadam lay are the main factors affecting the launching site displacement response,and all the three factors are inversely proportional to the displacement response.The elastic modulus of bituminous concrete in different intervals may lead to different sensitivity of launching site displacement response.

Key words:launching site;dynamic response;approximate model;sensitivity research

收稿日期:2015-12-17

作者简介:杨春浩(1991- ),男,博士研究生,研究方向为兵器发射理论与技术。E-mail:y674196@163.com。

中图分类号:TJ768.1

文献标识码:A

文章编号:1004-499X(2016)02-0087-06