构建数学模型,提高高中学生解决实际问题的能力
2016-07-15谢宁
谢宁


[摘 要] 在素质教育背景下,要求数学教学与实际生活相结合,以培养学生解决实际问题的能力.而构建数学模型,能很有效地提高学生分析问题和解决问题的能力,让学生运用所学的数学知识解决实际问题,这正好满足了素质教育的要求,让学生发现学数学的意义的同时也提高了学生的数学素养. 本文将深入探讨如何构建数学模型来解决一些数学实际问题.
[关键词] 数学模型;构建;解决实际问题
数学知识来源于生活,并最终应用于生活. 在现实的生活中经常会遇到一些需要数学知识来解决的问题. 但由于这些问题不能直接套用某种数学公式、某种定理或者某种解法,而需要将现实生活的实际情况进行简化、概括,并将其转化为数学语言,进而抽象表达成一个数学问题的过程,这就是构建数学模型的过程. 利用构建数学模型的方法来解决实际问题,可以培养学生利用数学的意识,使其创新精神在数学活动中得到体现和落实,对于以后应用于实践奠定了基础.
数学模型及构建程序
所谓数学模型,就是利用数学语言模拟现实的模型. 即把实际问题中的主要特征、主要关系抽象出来,用数学语言概括或近似地表述出来的一种数学结构. 这种解决问题的方法非常适用于某种特定的研究过程.对于高中数学来讲,它也是一门从现实生活中提取问题,通过解决问题来概括和总结出相关的数学公式、定理的学科,而这些前人得出的结论就是已构建的数学模型. 因此,将构建数学模型教学应用到高中数学教学中,实质上是树立学生构建数学模型的思维意识,让学生掌握构建数学模型的方法,然后利用所学知识解决从实际生活中抽象出来的数学问题.
数学模型在构建时,大致需要遵循四个步骤:一是观察与分析实际生活中的问题;二是将其转化成数学语言,并抽象出数学问题,即构建数学模型;三是求得此数学模型的解;四是把模型的解返回到现实问题中去,检验数学模型的符合程度或获得现实问题的解.
构建数学模型,提高学生的转换能力
在高中数学教学中,运用数学模型策略,实质上是一种思维方式的转换,它是将抽象的实际问题转换成逻辑思维,构建出数学模型,运用模型这一杠杆帮助学生解决数学问题的过程.
例:2014年北京时间7月14日,巴西世界杯决赛场上,德国队和阿根廷队为抢夺冠军展开了激烈的角逐. 如果你是某队的一位左边锋,那么你推进到距底线多远处射门,才可以使得射门角最大?(标准足球场长105米,宽68米,球门长7.32米)
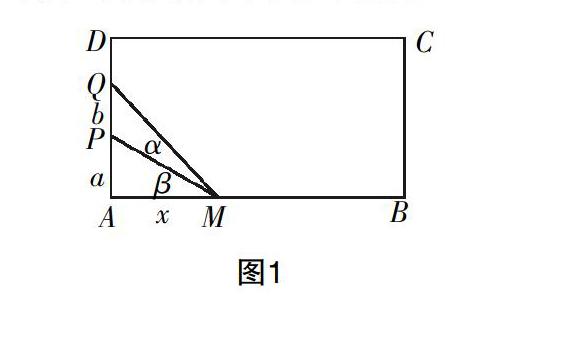
足球是大多数学生尤其是男生非常感兴趣的一项运动,他们中有一大批球迷,不但关心足球的输赢,而且对足球球技、战术也很有研究. 学生们虽然对此题很感兴趣,但是,仅仅看着这些文字会觉得束手无策,无从下手. 那么,解决这个问题的关键在哪里?关键就是一种思维的转换,构建数学模型,把它转化为数学问题. 但从何处入手呢?这时教师就需要引导学生分析,如:这是代数问题还是几何问题?如何确定球员与球门的位量关系?首先得按题意画出图形(如图1),于是很容易就构建出下面的模型并确定了问题的解法.
构建数学模型,提高学生的创新能力
由于构建模型需要从实际案例中提取数学问题,因此,它兼具抽象性与实质性,要求学生具备抽象思维能力、逻辑思维能力与创新能力. 这样有助于规避传统“填鸭式”教学模式的弊端,能够有效促进学生创新能力的提高.
例:日本东京晴空塔,又名为东京天空树,是全世界最高的自立式电波塔,高634米. 若把它的信号传播到550千米外的大阪,行吗?(地球半径6371米)若用一座电波塔直接从东京传输到大阪,须建高度为多少米的电波塔?
这样一个既有常识性又带科学性的问题,是培养学生数学直觉思维和创新能力的好材料.如何通过建模来回答呢?
首先要将电波塔及电波信号的传输,扩大想象到整个地球空间,展开空间想象,抽象出相应的数学模型. (如图3所示)
这大约是3座珠穆朗玛峰的高度,建造如此高的电波塔显然是不现实的. 同时告诉学生,解决这类长距离信号传输问题,往往不去盲目地一味增高电波塔的高度,而是通过多个中继站“接力”的方式或用通信卫星的手段.
此数学模型很好地解决了一个实际问题,让学生增加了数学直觉思维和用数学的意识,提高了学生用数学去解决实际问题的能力,触类旁通,对知识的理解和应用更加深刻.
从理论上来讲,构建数学模型的过程实质上是一个创造的过程. 教师与学生一起分析已知的条件,从中提炼有效信息,而后抽象与创造出具体的数学问题,最后解决问题.这样的创造过程体现了素质教育对高中数学的要求,将高中数学与实际生活相结合,培养了学生从实际生活中发现问题进而解决问题的能力.
引申:(2009·宁夏)为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤. (本题考查的是解三角形的实际应用及构造函数模型解决实际问题的能力.)
构建数学模型,培养学生用数学解决实际问题的意识,激发主动探索实际问题的欲望
一天放学时,突然倾盆大雨,同学们纷纷跑回家,唯独某同学仍不慌不忙地漫步雨中. 大家都笑他怎么这么傻,他笑着答:“你们才傻呢,前面不也下着雨吗?跑什么?反正我到家的路永远都是那么长,无论我跑多快,这段路程又不会减少?”那么,在下雨天,到底是快快跑淋雨多呢还是慢慢走淋雨多呢?
这个实际问题的提出肯定会引起很多学生的兴趣.学生们也肯定一起笑话那个漫步雨中的同学是傻子,因为总的淋雨量不会与行走的路程成正比,因为雨不是静止在空中的,它是一个动态的连续的过程,你哪怕一步不走,路程为零,你还是会被淋成落汤鸡.那是不是总的淋雨量与淋雨时间成正比呢?然而生活经验告诉我们,当我们下雨天坐在车里的时候,车速越快,打落在车窗上的雨滴会越来越大,越密,感觉淋雨量也越大,所以我们还不能够简单地认为跑得越快,总的淋雨量就越少.那到底下雨时候我们怎么走才能使淋雨量最少呢?
为了方便研究这个实际问题,我们将该人视作长方体,那么只需要考虑上底面和侧面的受雨情况;其次,不妨设人以匀速直线运动的方式行走,雨速和降雨的角度也是不变的. 我们可将代表人体型的长方体,雨竖直向下的分速度、人运动的路程,这些与人体运动速度无关的量都看作是常量;将人运动的速度和总的淋雨量看成是变量;而将降雨水平方向的分速度看成影响总淋雨量的参量. 适当对常量和参量赋值后,构造出如下数学问题:
如图5,长方形物体E在雨中沿面P(面积为S)的垂直方向做匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R). E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与v-c×S成正比,比例系数为;(2)其他面的淋雨量之和,其值为则应该保持与雨的水平分速度相同的速度行走,此时,并不是跑得越快,总淋雨量就越小.
可见,数学建模是数学学习的一种新的创新的方式,它为学生们提供了自主学习的空间,有助于学生体验数学在解决实际问题中的价值和作用,体验数学与日常生活的联系,体验运用知识和方法解决实际问题的过程,增强了应用意识,有助于激发学生学习数学的兴趣和探究数学问题的欲望,发展学生的创新意识和实践能力.
