Pegels模型在软件可靠性中的预测研究

陈　路，胡贤德

(安徽新华学院信息工程学院，安徽合肥 230088)



Pegels模型在软件可靠性中的预测研究

陈路，胡贤德

(安徽新华学院信息工程学院，安徽合肥 230088)

[摘要]为了更好地对软件可靠性进行预测，本文首先分析了常用的Pegels模型和阻尼Pegels指数平滑模型，然后根据软件可靠性准则误差平方和(SSE)建立数学最优化模型，计算出最优拟合度对应的最优的平滑系数。实验表明,在进行软件可靠性预测时，以Tandem计算机数据集为例，Pegels模型的拟合精度较高，且阻尼Pegels模型的拟合度优于Pegels模型，最优拟合度对应的平滑系数值也从平滑系数的经验选取法上都得到了验证。

[关键词]Pegels模型；软件可靠性；误差平方和准则；平滑系数

计算机软件在社会发展中发挥着举足轻重的作用，社会对软件的依赖性也越发强烈，随着软件规模日益扩大，其可靠性越发难以保证，对软件可靠性的预测[1]显得尤为重要。

对于软件可靠性的建模问题，国内外的专家和学者一直在进行深入的研究和探索。黎锁平[2]等人分别将单指数平滑法和双指数平滑法用于通信软件的可靠性预测，并得出双指数平滑模型预测更加准确的结论。刘龙[3]等人将双指数平滑法进行改进，建立了随时间变动的平滑系数模型，并对软件可靠性进行预测，得到了较好的定性预测结果，结果未能用软件可靠性准则定量衡量。

本文将在分析常用的指数平滑模型——Pegels模型和阻尼Pegels模型的基础上，对软件的失效数据进行SSE准则可靠性定量建模，求出最优的指数平滑系数，对失效数据进行可靠性预测。

1指数平滑模型

指数平滑模型对于一些统计空间模型来说是最优的模型，而且简单可靠易于操作，尤其适用于一些随时间连续变化的数据。下面就几种最常用的指数平滑模型[4]作简单介绍。

1.1Pegels模型趋向于被作为趋势序列的通用模型

St=αXt+(1-α)(St-1Rt-1).

(1)

Rt=γ(St/St-1)+(1-γ)Rt-1.

(2)

(3)

1.2阻尼Pegels模型趋向于被作为趋势序列的通用模型

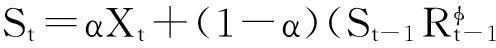
(4)

(5)

(6)

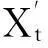
在指数平滑模型的预测中，最重要的就是平滑系数的选取，因为这些系数能在很大程度上影响模型的预测精度。在平滑系数选择方法上，主要采用经验的方式进行人工选择。以α取值的选择为例，通常依赖于经验[5]，根据以下情况选取：当统计数据波动不大时，α可取0.1～0.3，以加重原来预测值的权重；当统计数据波动较大时，α可取0.6～0.8，以加重新预测值的权重；当难以判断时，可以先采用几个不同的α值加以试算比较，再选取最优α值。

显然仅靠经验选择平滑系数进行预测必然会影响预测结果，可以考虑建立相应的数学模型，寻找最佳预测结果对应的平滑系数值，从而对软件可靠性进行定量预测。

2数学模型的建立

衡量软件可靠性的预测精度有四种常用的准则[1]，即误差平方和准则(SSE)、均方误差准则(MSE)、赤池信息量准则(AIC)和预测比例风险准则(PRR)。对于上述四种准则而言，在同一数据集上得出的值越小，表明模型的拟合程度越低。考虑到误差平方和准则是误差分析的综合指标之一。本次实验采用误差平方和SSE准则作为模型的评价指标，建立如下优化模型。

(7)

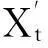
根据Pegels和阻尼Pegels模型的公式(1)～(6)可以找出相应的约束条件，令初步预测值S0初值为X1，局部增长值R0初值为前三个局部增长比例的均值。

由此建立了上述目标函数，接下来就可以选取合适的数据集，再根据约束条件进行模型的预测应用。

3模型在软件失效数据集上的应用

前面根据Pegels模型和阻尼Pegels模型分别建立了数学模型，接下来就可以使用模型去模拟软件失效数据集。本模型使用了Tandem计算机数据集[1]，详见表1。

表1　Tandem计算机软件失效数据集

本实验在Matlab软件中进行，分别用Pegels模型和阻尼Pegels模型计算了最优SSE准则值对应的20个测试时间的错误数预测值，详见表2。

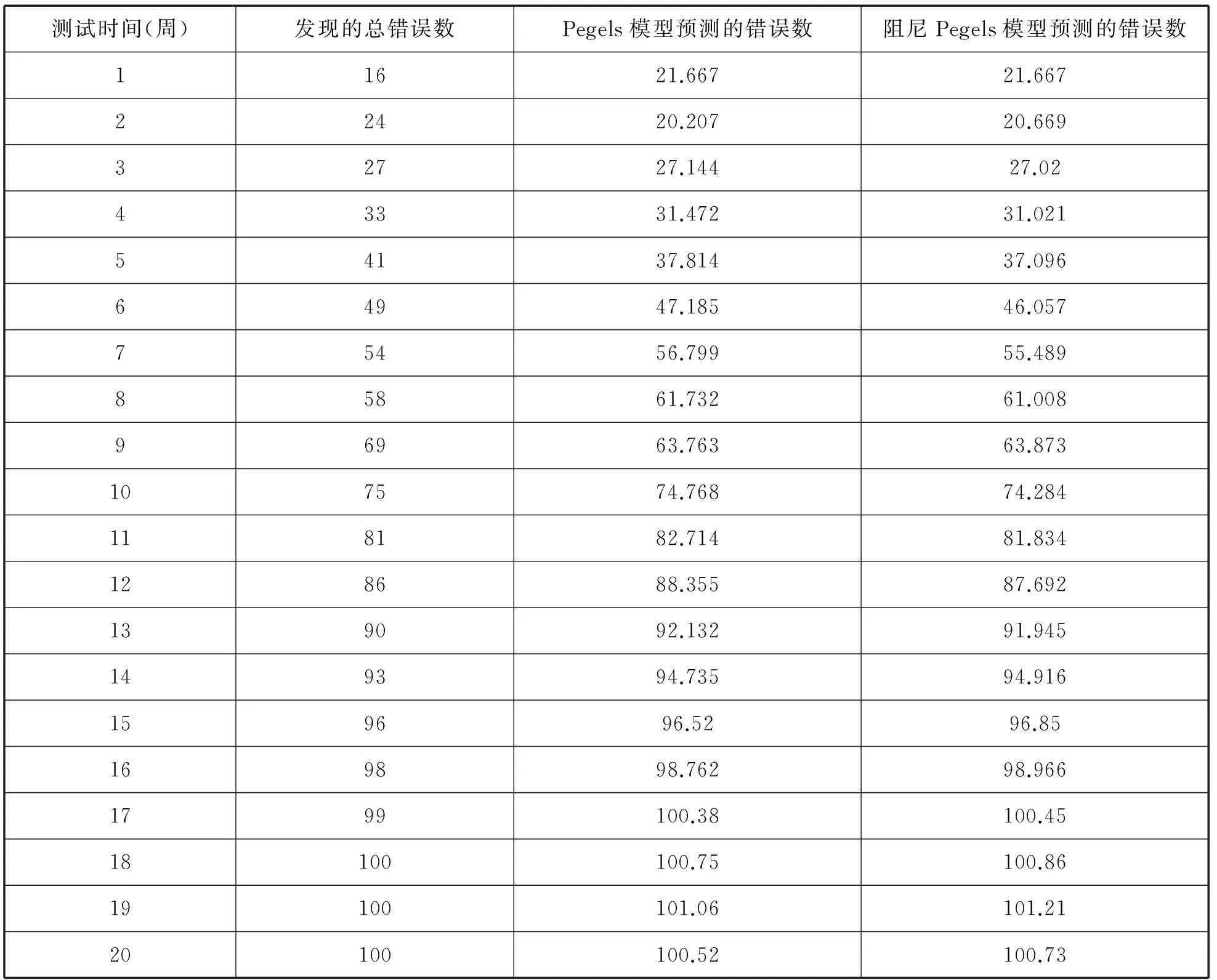
表2　使用Tandem计算机数据的模型预测对比表

从表2可以看出，使用Pegels模型和阻尼Pegels模型等指数平滑模型更好地预测了软件的错误数据。对于SSE准则而言，在同一数据集上得出的值越小，表明模型拟合度越高[1]。从表3中模型间的SSE准则对比值可以看出，无论是Pegels指数模型还是阻尼Pegels指数模型，都比GO模型、PNZ模型和NHPP模型等具有更好的拟合度和预测能力，其中阻尼Pegels模型优于基本Pegels模型。

其中采用Pegels模型和阻尼Pegels模型预测时，最优SSE准则值所对应的平滑系数α、γ和φ值分别如表4所示。

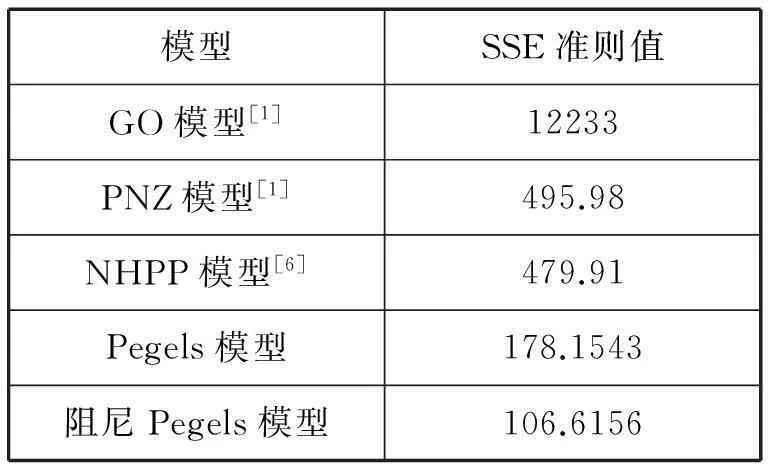
表3　模型间的SSE值对比表

表4　Pegels模型和阻尼Pegels模型参数值

从表4不难看出，两个模型预测得到的最小SSE对应的α为0.64和0.66，最优α取值显然符合经验判断法中给出的取值范围0.6～0.8。

为了更清晰地观察预测值和实际值之间的拟合程度，根据软件实际错误数据和Pegels模型、阻尼Pegels模型预测数据，可以得到如图1所示的曲线图。

图1　Pegels和阻尼Pegels预测值与软件实际值对比图

从图1可以看出，Pegels模型和阻尼Pegels模型对软件失效数据集的实际拟合度较高，预测效果好，可以有效地对软件失效数据进行预测，其中阻尼Pegels模型的预测效果优于Pegels模型。

4结语

本文首先讨论了常用的指数平滑模型——Pegels和阻尼Pegels模型，然后通过软件可靠性的SSE准则建立数学模型，并在Tandem数据集上进行拟合，用Matlab软件计算出最小的SSE值和相应的最优平滑系数，以此来进行软件可靠性的预测。计算结果显示，在使用最优的平滑系数时，Pegels模型和阻尼Pegels模型的预测精度比该数据集上之前使用的GO模型、PNZ模型和NHPP模型的精度高很多，同时阻尼Pegels模型的预测精度比Pegels模型的精度高，在软件可靠性的拟合效果上最佳。

[参考文献]

[1]Hoang Pham.系统软件可靠性[M].李璐祎,译,北京:国防工业出版社,2014:157,181.

[2]黎锁平,武会超.基于双指数平滑方法的通信软件可靠性分析[J].兰州理工大学学报,2006,32(4):102-104.

[3]刘龙,徐池.基于改进的双指数模型的软件可靠性预测研究[J].可靠性技术,2014(1):14-17.

[4]蔡凯达.基于指数平滑和人工智能算法的预测[D].兰州:兰州大学,2013.

[5]王长江.指数平滑法中平滑系数的选择研究[J].中北大学学报:自然科学版,2006,27(6):558-561.

[6]谢景燕.考虑不完美排错情况的NHPP类软件可靠性增长模型[J].软件学报,2010,21(5):942-949.

Prediction of Software Reliablity Based on Pegels Model

CHEN Lu, HU Xian-de

(College of Information Engineering, Anhui Xinhua University, Hefei Anhui 230088, China)

Abstract:The prediction of software reliability was discussed in the paper. Firstly, the paper analyzed exponential smoothing model which is widely used Pegels model and damped Pegels model. Then，mathematical model was built based on the sum of squared errors of software reliability rule. Finally,the best smoothing factor was calculated while the minimum value of SSE has got. The experiments show that the Pegels model is preciser in software reliability prediction on Tandem set, and the result of damped Pegels model is better than Pegels model, which is validated from the smoothing factor decided by experience.

Key words:Pegels model; software reliability; sum of the squared errors rules; smoothing factor

[收稿日期]2016-04-17

[基金项目]安徽省质量工程“计算机科学与技术(IT服务外包方向)”(2013ZY084)。

[作者简介]陈路(1983- )，女，讲师，硕士研究生，从事软件可靠性、数学建模研究。

[中图分类号]TP311

[文献标识码]A

[文章编号]2095-7602(2016)06-0046-04