模块网络上伊辛模型成核的最优外场分配

李　庆，周翠琴，陈含爽

(安徽大学 物理与材料科学学院, 安徽 合肥 230601)



模块网络上伊辛模型成核的最优外场分配

李庆，周翠琴，陈含爽

(安徽大学 物理与材料科学学院, 安徽 合肥 230601)

摘要：本文讨论了伊辛模型在具有两个模块的网络上的成核相变。对每个模块施加不同的外场强度，在保证平均外场不变的前提下研究外场差异对成核速率的影响。通过平均场理论计算和伞形采样模拟，发现存在一个最优的外场差异对应成核速率最大。

关键词：成核；相变；模块网络；伊辛模型

DOI：10.13757/j.cnki.cn34-1150/n.2016.02.006

相变和临界现象是统计物理研究所关注的重要传统课题[1-3]，其关键科学问题是要回答复杂的相互作用如何影响相变和临界现象，如有序-无序相变、渗流、自组织临界性、非平衡相变等。然而，先前的工作大多数都关注如何得到相变点和拓扑及其与尺度的关系，而关于相变发生的动力学过程却鲜有报道。众所周知，自然界大部分相变是通过成核过程所激发的，如雨的形成、结晶过程、玻璃材料形成、蛋白质折叠等[4]。成核是涨落驱动的从亚稳态到稳态的弛豫过程，也就是新相的孕育过程。然而，几乎所有工作都在关注欧氏空间成核问题，而许多实际体系可以通过形形色色的网络来描述，一个自然的问题是复杂网络拓扑如何影响相变动力学。在前期工作中，针对一些统计物理模型初步探讨了复杂网络上成核相变问题[5-9]。本文将研究伊辛模型在模块网络上的成核问题，解决如何通过分配外场来达到成核速率最优化的问题。

1模型建立

伊辛模型是描述相变的基本模型，由物理学家Wilhelm Lenz在1920年提出，并以他的学生Ernst Ising命名。自然界的许多现象可以通过伊辛模型来理解，如合金中的有序-无序转变、液氦到超流态的转变、液体的冻结和蒸发、晶格气体、玻璃物质的性质、森林火灾、城市交通、蛋白质分子折叠等。伊辛模型的哈密顿量

(1)

式中Jij>0是节点i和节点j之间的耦合强度，取Jij=J=1,∀i,j；si是节点i的自旋变量，可以取自旋向上si=+1或自旋向下si=-1；hi是施加在节点i上的外场强度；aij是网络邻接矩阵元，当节点i和节点j存在一条边相连时，aij=1，否则aij=0。

如图1所示，考虑由两个模块组成的网络，为简单起见，每个模块的节点数目相同，即NⅠ=NⅡ=N/2，N为网络大小。每条边以1-p的概率随机地连接同一模块的两个节点，以p的概率随机地连接不同模块的两个节点。因此，参数p可以控制网络模块性的好坏：p越小，网络模块性越好。对属于同一个模块的节点，施加相同的外场，而对属于不同模块的节点，外场可以是不同的。为了保证总外场强度不变，假设第1个模块的外场hⅠ=h-δ，第2个模块的外场hⅡ=h+δ，其中h>0，δ∈[0,h]。为了研究成核问题，设定体系温度T小于相变温度，初始自旋构型取大部分自旋取向朝下(亚稳态)。显然，体系更加稳定的状态是大多数自旋取向朝上，涨落会驱动体系从亚稳态成核相变到稳态。我们感兴趣的是外场差异对成核速率和成核路径的影响。

图1　具有两个模块的网络示意图，

2平均场理论

令mⅠ和mⅡ分别为模块I和模块II的平均磁矩，首先将体系的哈密顿量写成3个部分

H=HⅠ,Ⅰ+HⅡ,Ⅱ+HⅠ,Ⅱ

(2)

其中HⅠ,Ⅰ和HⅡ,Ⅱ分别为模块I和模块II内部的能量，HⅠ,Ⅱ是模块I和模块II之间的能量。根据平均场理论，这3个部分可以近似表达为

(3)

这里MⅠ,Ⅰ=MⅡ,Ⅱ=〈k〉N(1-p)/4是模块I和模块II内部连边的数目，MⅠ,Ⅱ=〈k〉Np/2是模块I和模块II之间连边的数目，〈k〉是网络平均度。体系的熵可以写成S=NⅠSⅠ+NⅡSⅡ，其中SⅠ和SⅡ分别是模块I和模块II单个节点的熵，表达式：

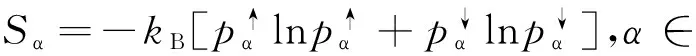
(4)

(5)

其中，β=1/(kBT)是温度的倒数，kB是玻尔兹曼常数。通过牛顿迭代法可以数值求解方程组(5)。图2给出了在p=0.01，h=1.0，δ=0.5时单个节点的平均自由能F/N等高线。图中用符号标记了自由能取极值时，方程组解的位置，其中方框标记4个稳定的节点，圆圈标记4个鞍点，星形标记不稳定节点。体系的最初状态处于左下角稳定节点的位置，而体系的最终状态处于右上角稳定节点的位置。另外，体系从一个稳定节点过渡到另一个稳定节点时必然要经过一个鞍点。可以看出，从初态到末态有两条可能的成核路径，如图中箭头所示，每条路径都需要经历一个中间亚稳态的两步成核过程，即其中一个模块先成核相变，然后另一个模块再成核相变。由于外场大的那个模块一般先成核，所以其中一条路径的概率几乎为零。

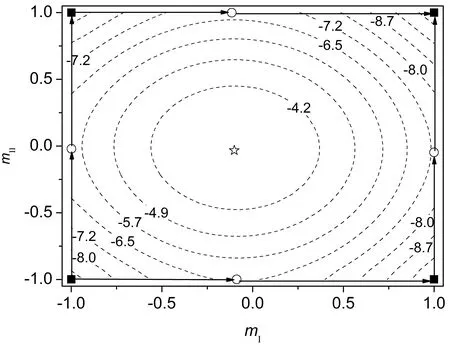
图2　单个节点的平均自由能等高线

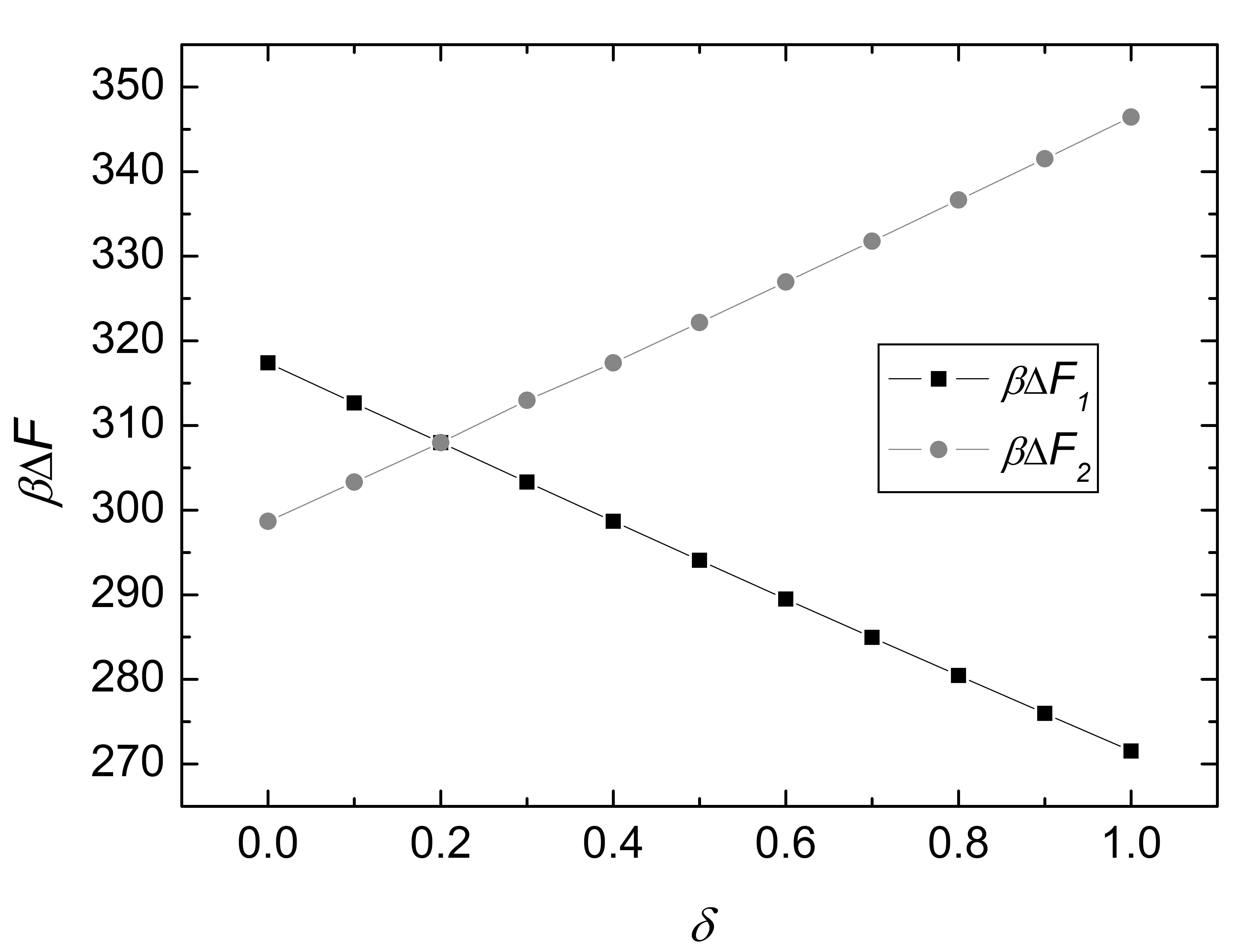
图3　第1步和第2步成核的自由能垒

3伞形采样

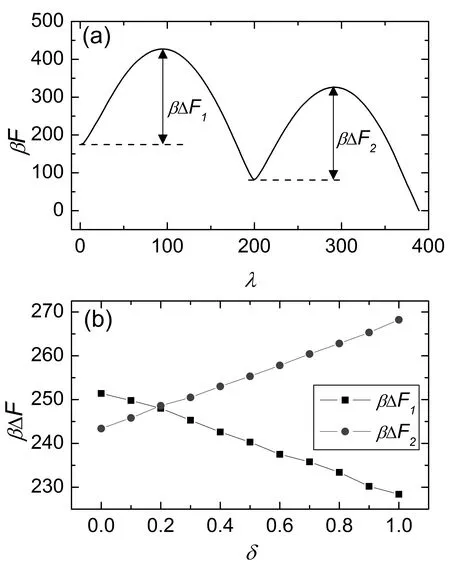
图4　伞形采样结果。(a)自由能随λ变化曲线，

4结论

通过平均场理论和伞形采样，本文研究了伊辛模型在具有两个模块的网络上的成核相变问题。在不改变平均外场的前提下通过改变两个模块上外场强度的差异，我们发现存在一个中等大小的差异值对应的成核速率最大。从本文结果可以看出，外场的分配可以调控网络体系的成核速率，适当的分配原则可以使速率最大化。因此，如何分配外场对相变的发生至关重要。

参考文献:

[1] Dorogovtsev S N,Goltseve A V,Mendes J F F.Critical phenomena in complex networks[J]. Rev Mod Phys,2008, 80(4):1275-1335.

[2] Arenas A,Diaz-Guilera A,Kurths J, et al.Synchronization in complex networks[J].Phys Rep,2008, 469(3): 93-153.

[3] Pastor-Satorras R,Castellano C,Mieghem P V,et al.Epidemic processes in complex networks[J].Rev Mod Phys, 2015, 87(3): 925-979.

[4] Kashchiev D. Nucleation: Basic Theory with Applications [M].Butterworths-Heinemann, Oxford, 2000: 1-480.

[5] Chen H S,Shen C S,Hou Z H,et al.Nucleation in scale-free networks [J].Phys Rev E,2011, 83(3): 031110.

[6] Chen H S,Hou Z H.Optimal modularity for nucleation in network-organized Ising model [J]. Phys Rev E, 2011, 83(4): 046124.

[7] Shen C S,Chen H S,Ye M L, et al.Nucleation pathways on complex networks [J]. Chaos, 2013, 23(1): 013112.

[8] Chen H S,Li S X,Hou Z H, et al.How does degree heterogeneity affect nucleation on complex networks? [J].J Stat Mech:Theo & Exp,2013, 9: 09014.

[9] Chen H S,Shen C S.Nucleation of a three state spin model on complex networks[J]. Physica A,2015, 424: 97-104.

[10] Van Duijneveldt J S,Frenkel D.Computer simulation study of free energy barriers in crystal nucleation [J]. J Chem Phys,1992, 96(8): 4665-4668.

Optimal Allocation of External Fields for Nucleation of Ising Model on Modular Networks

LI Qing, ZHOU Cui-qin, CHEN Han-shuang

(School of Physics and Material Science, Anhui University, Hefei, Anhui 230601, China)

Abstract:This paper discusses the nucleation in a first-order phase transition on a network with two modules. By applying two distinct external fields to each module, the effect of the diversity in external fields on nucleation rate is investigated under the constraint that the average external field is unchanged. By mean-field theory and umbrella sampling, we find that there exists an optimal diversity for which the nucleation rate is maximal.

Key words:nucleation; phase transition; modular networks; Ising model

* 收稿日期：2015-09-08

基金项目：国家自然科学基金(11205002)和大学生科研训练计划项目(J18520121)。

作者简介：陈含爽，男，安徽桐城人，博士，安徽大学物理与材料科学学院副教授，研究方向为统计物理与复杂系统。 E-mail: chenhshf@mail.ustc.edu.cn

中图分类号：O414；O415

文献标识码：A

文章编号：1007-4260(2016)02-0019-03

网络出版时间：2016-06-08 12:57网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160608.1257.006.html