幅相调制信号的星座图恢复与调制方式识别*

陆珊珊，王　伟，王国玉

(1.国防科技大学 电子科学与工程学院， 湖南 长沙　410073；2.国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙　410073)



幅相调制信号的星座图恢复与调制方式识别*

陆珊珊1,2，王伟1，王国玉1

(1.国防科技大学 电子科学与工程学院， 湖南 长沙410073；2.国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙410073)

摘要：针对幅相调制信号的调制方式识别问题，提出一种基于星座图恢复的算法。该算法估计信号载频及信噪比等参数，并依据波特率和符号定时完成对接收信号的波特率采样；采用一种非数据辅助载频偏差估计方法，以消除载频偏差及相位偏移对星座图恢复的影响；利用平均似然比检测的方法，完成幅相调制信号调制方式的识别。仿真结果表明，与仅考虑信号幅值分布的极大似然算法相比，该算法具有识别性能更优。

关键词：调制识别；偏差估计；星座图；最大似然

根据对接收信号的分析，调制方式识别技术能够自动地判定发射信号的调制方式。该技术在电子侦察、频谱监测、自适应接收、智能通信等方面有广泛的应用，在军事和民用领域均具有十分重要的意义[1-7]。

由于具有较高的频谱效率，多进制正交幅相调制(MultipleQuadratureAmplitudeModulation,MQAM)信号在卫星和微波通信中得到了广泛的应用[8]。针对该类信号调制方式的识别问题，目前研究较多的是基于信号幅值分布的方法。复旦大学奚家熹等[9]对信号幅值做减法聚类，并根据聚类中心数目判定信号的调制方式。张路平等[10]计算信号矢量图中最小环带的方差，随后依据相应阀值识别信号的调制方式。廖灿辉等[11]构造了信号幅值分布模板，并通过实际幅度分布与模板间的匹配误差来进行调制方式识别。文献[12-13]利用信号幅值概率密度构造似然函数以识别信号的调制方式。然而，实际信号的调制信息综合反应在幅值和相位分布上，仅利用幅值信息，其性能十分有限。

星座图综合反映了已调信号幅值和相位的分布信息，是调制识别方面较为重要的依据之一。基于信号星座图识别算法的关键问题是消减载频估计偏差对星座图的影响。为解决此问题，谭晓波等[14]采用相位差分方法以抑制载频偏差引起的星座图扩散，然而该算法仅适用于多进制相移键控(MultiplePhaseShiftKeying,MPSK)信号。程汉文等[15]采用盲分离方法以修正载频偏差对星座图的影响，然而该算法仅适用于较小的频率偏移。针对上述情况，引入一种非数据辅助载频偏差估计方法[16-17]，提高了算法对载频偏差的容忍程度，能够较好地恢复常见MQAM信号星座图。采用平均似然比检测方法对信号调制方式进行识别，具有较好的识别性能。

1信号模型

MQAM信号在现代通信系统中得到了较为广泛的应用。假定{sn=snI+jsnQ}表示信号源第n个符号周期发射的符号，则发射信号的解析形式可以表示为：

(1)

其中，g(t)为脉冲成形滤波器冲激响应，Tb为符号周期，fc和φ分别为载波频率和相位。信号经加性高斯白噪声信道后被接收端采样接收，接收信号可以表示为：

exp[j(2πfckTs+φ)]+w(kTs)

(2)

其中，Ts为采样周期，w(kTs)为复数高斯白噪声，εTb为采样定时误差。

2信号预处理

为便于后续处理，应先对接收信号进行预处理，其主要流程如图1所示。系统估计接收信号载频及信噪比，并将接收信号下变频至基带；随后估计信号波特率，调整采样速率为波特率整数倍，并结合码元定时进行重采样，以获得码元同步序列用于后续处理。

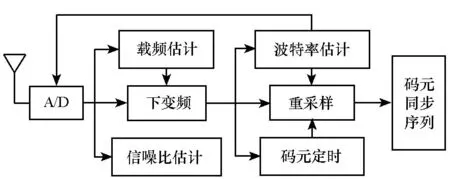
图1　信号预处理流程Fig.1　Signal pretreatment process

2.1载频和信噪比估计

载频估计是信号下变频处理的基础，相对于时域载频估计算法，频域估计算法具有较好的稳健性。不考虑噪声时，MQAM基带信号的功率谱可表示为[18]：

(3)

(4)

其中，R(f)为接收序列功率谱密度，fs为采样频率，N为采样点数。在实际应用中，可以先提取频谱较强部分后再利用频率居中法，以改善低信噪比下算法的估计性能。

信噪比为信号强度和背景噪声的比值，获取该参数有利于改进识别算法的性能。本文采用一种快速信噪比估计算法[18]，该算法的主要步骤为：①对信号功率谱进行均值滤波；②依据设定的规则，估计信号对应频谱的上限fH和下限fL；③对上述频率范围外的噪声谱图进行直方图统计，得出噪声谱均值N0；④利用下列式(5)估计信号的信噪比：

(5)

其中，R(f)-N0为去噪声信号功率谱。该算法对先验信息要求较低，具有较好的鲁棒性，适用于本文所考虑的调制信号类型。

2.2波特率估计和符号定时

波特率估计是进行码元同步采样的关键技术。MQAM信号包络平方统计均值se(t)的傅里叶变换可表示为[14]：

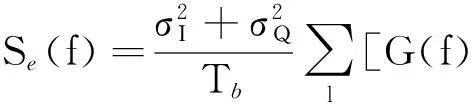
(6)

恢复信号星座图需要进行符号定时，其任务是确定最佳的采样时刻。此处采用一种基于包络的平方的定时算法，具体公式为[11]：

(7)

其中，L为用于此次定时估计的采样点数，fb为波特率。根据公式估计的定时偏差修正原有的采样时刻，即可完成码元定时。在算法实际应用过程中，应每隔一段时间重新进行符号定时以避免误差的累积。

3星座图恢复

3.1频率偏移对星座图的影响

接收信号经预处理后，输出码元同步序列的解析形式可以表示为：

(8)

其中：E为信号平均功率，不失一般性；令E=1；Δfc为载频估计偏差。不考虑噪声的影响，当Δfc非零时，k和k+1时刻接收序列y(k)的绝对相位分别为：

(9)

其中，θk和θk+1为相应时刻符号相位，φ又称为相位偏移。由式(9)可知，除符号信息相位变化外，相邻时刻相位还包含偏移量2πΔfcTb，该偏移量的累积使得信号散点图呈现环状，从而影响星座图的恢复，如图2(a)所示。

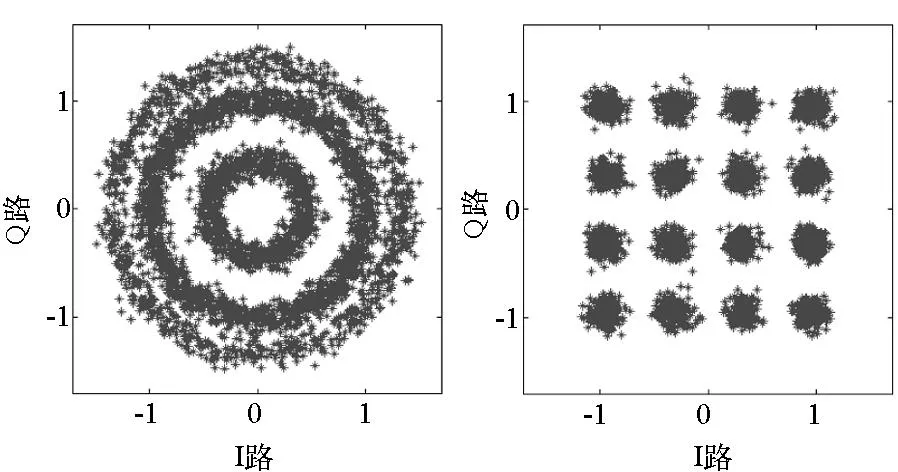
(a) 2πΔfcTb=0.001　　　(b) 2πΔfcTb=0,φ=0图2　16QAM信号散点图Fig.2　16QAM signal scatter plot

3.2载频偏移估计

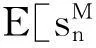
x(k)M=AMexp[j(Mwck+φ)]+e(k)

(10)

(11)

3.3星座图恢复

(12)

4平均似然比识别算法

消除载频偏移和相位偏移后，码元序列能够较好地反映信号星座图的分布特征。此时码元同步序列可以表示为：

(13)

识别算法通过对上述序列进行分析，从C种备选调制方式中选出正确的类型，该过程可以被视为一个多元假设检验问题：

Hc: y=s(c)+v， c=1, 2, …, C

(14)

根据检测理论可知，在备选调制方式先验等概时，最大似然方法在贝叶斯最小错误概率准则下是最优的。利用序列yk构造似然函数，高斯噪声情形下，yk的概率分布为：

(15)

需要注意的是yk和sk均为复数形式。根据平均似然比检测理论，假定调制方式为Hc时，yk的条件似然函数应在s(c)上取平均：

(16)

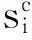
(17)

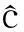
5仿真分析

为验证所提算法的有效性，设计了两组仿真实验。相对于盲分离频偏估计方法，第一组用于验证本文算法具有更大的适用范围；相对于仅考虑幅值分布的极大似然方法，第二组用于验证本文算法具有更好的识别性能。

仿真中备选调制方式为{4QAM，16QAM，32QAM，64QAM}。载频设置为1MHz，采样速率为4MHz，码元速率为125kHz，采样时长为2000个码元周期。由于码元定时每隔一段时间重新进行，因而定时误差不会累积，对信号星座图恢复影响较小。因此本文不考虑定时偏差的影响，假定码元定时是精确的。

仿真1设定频偏ΔfcTb为{0.1, 0.01, 0.001}三个档次。备选调制方式中32QAM为十字形星座，其余为方形星座。仿真中将十字形星座归为一类，方形星座归为一类，其性能为3种信号的均值，图3给出了非数据辅助(NonDataAided,NDA)频偏估计算法的性能曲线。图4给出了盲源分离(BlindSourceSeparation,BSS)频偏估计算法[15]的性能曲线。

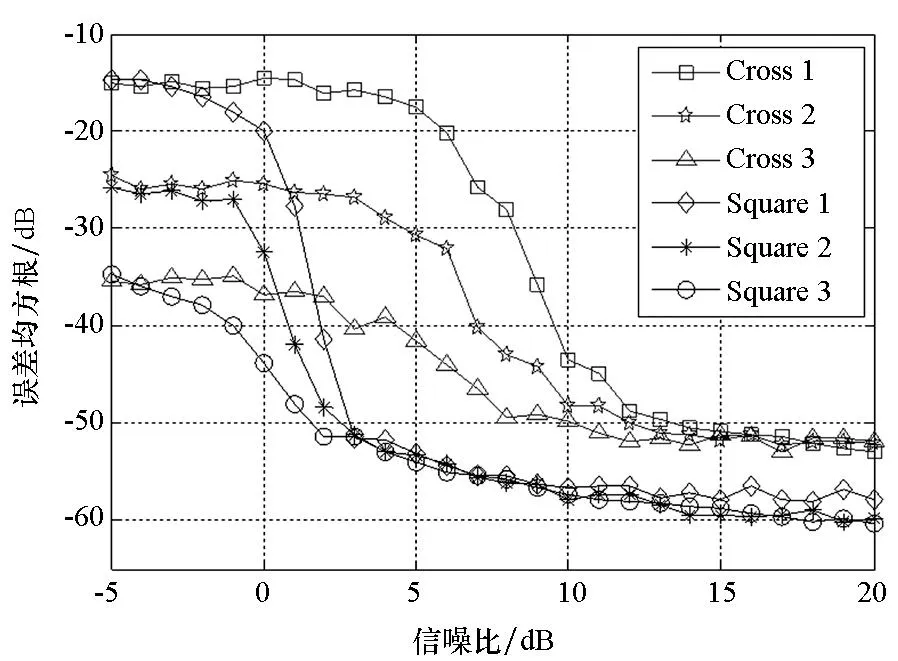
图3　非数据辅助算法的估计性能Fig.3　Estimation performance of the NDA method

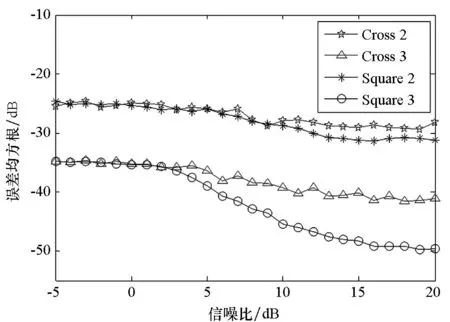
图4　盲源分离算法的估计性能Fig.4　Estimation performance of the BSS method

当频偏处于0.1档时，盲源分离频偏估计算法完全失效，因此图4仅包含0.01和0.001档时算法的估计性能曲线。对比图3和图4可知，本文算法能在较大频偏范围内对载频偏差进行估计，且具有更好的估计性能。而盲源分离频偏估计算法仅在频偏较小且输入信噪比较大时，对信号具有一定的估计精度。

仿真2设定信号信噪比范围为0～15dB，每个信噪比实验进行500次蒙特卡洛仿真，记录算法正确识别的次数，以衡量该性噪比下算法的识别概率。文献[12]提出的基于信号幅值分布的极大似然算法具有较好的性能，本文选择该算法作对比。图5所示为本文算法和对比算法的性能比较，图中标识后缀1为本文所提算法，后缀2为对比算法。

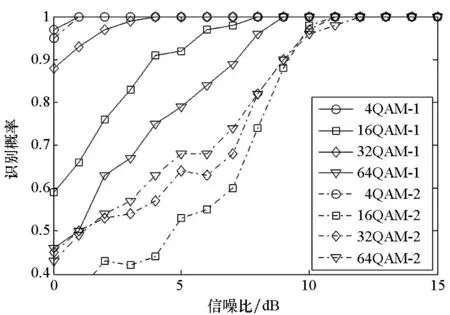
图5　不同算法的识别性能Fig.5　Recognition performance of different algorithms

由图5可知本文算法在信噪比为9dB时能完全正确识别全部4种信号，而对比算法则需要12dB才能完全正确识别。同时还可以看出对比算法在信噪比为8dB左右时，难以有效识别较高调制阶数的信号，这是由于此时该类信号幅值分布十分接近的缘故，而本文算法此时已能较为有效地识别信号。

综合仿真1和仿真2的结果可知，本文算法能够适应较大载频估计偏差，对信号调制方式具有较好的识别性能，在输入信号信噪比较低的情形下具有较大的优势，从而证明了本文算法的适用性和有效性。

6结论

研究MQAM信号调制方式的识别问题，提出一种基于星座图恢复的算法。该算法能够较好地克服载频估计偏差对信号调制识别造成的不利影响；并且通过平均似然比检测的方法对信号调制方式进行识别，具有较好的识别性能。仿真结果证明了算法的适应性和有效性。需要指出的是，该算法对圆形星座信号适用性较差，如何提高算法对各类信号的适用性将是下一步研究的重点。

参考文献(References)[1]Nandi A K, Azzouz E E. Algorithms for automatic modulation recognition of communication signals[J]. IEEE Transactions on Communications, 1998, 46(4): 431-436.

[2]MobasseriBG.Digitalmodulationclassificationusingconstellationshape[J].SignalProcessing, 2000, 80(2): 251-277.

[3]DobreOA,AbdiA,Bar-NessY,etal.Surveyofautomaticmodulationclassificationtechniques:classicalapproachesandnewtrends[J].IETCommunications, 2007, 1(2): 137-156.

[4]XuJL,SuW,ZhouMC.Likelihood-ratioapproachestoautomaticmodulationclassification[J].IEEETransactionsonSystem,ManandCybernetics, 2011, 41(4): 455-469.

[5]HameedF,DobreOA,PopescuD.Onthelikelihood-basedapproachtomodulationclassification[J].IEEETransactionsonWirelessCommunication, 2009, 8(12): 5884-5892.

[6]吴月娴, 葛临东, 许志勇. 基于累积量的MPSK分类算法性能分析[J]. 系统工程与电子技术, 2007, 29(10): 1757-1761.

WUYuexian,GELindong,XUZhiyong.Performanceanalysisforcumulant-basedMPSKclassificationalgorithm[J].SystemsEngineeringandElectronics, 2007, 29(10): 1757-1761. (inChinese)

[7]陆凤波, 黄知涛, 易辉荣, 等. 一种基于高阶累积量的数字调相信号识别方法[J]. 系统工程与电子技术, 2008, 30(9): 1611-1615.

LUFengbo,HUANGZhitao,YIHuirong,etal.Recognitionalgorithmofphaseshiftkeyingsignalsbyhigher-ordercumulants[J].SystemsEngineeringandElectronics, 2008, 30(9): 1611-1615. (inChinese)

[8]詹亚锋, 曹志刚, 马正新.M-QAM信号的调制制式识别[J]. 通信学报, 2004, 25(2): 68-74.

ZHANYafeng,CAOZhigang,MAZhengxin.ModulationclassificationofM-QAMsignals[J].JournalofChinaInstituteofCommunications, 2004, 25(2): 68-74. (inChinese)

[9]奚家熹， 王宗欣. 基于Hilbert变换的MQAM信号调制体制识别[J]. 通信学报, 2007, 28(6): 1-6.

XIJiaxi,WANGZongxin.MQAMmodulationschemerecognitionusingHilberttransform[J].JournalonCommunications, 2007, 28(6): 1-6. (inChinese)

[10]张路平, 王建新.MQAM信号调制方式盲识别[J]. 电子与信息学报, 2011, 33(2): 332-336.

ZHANGLuping,WANGJianxin.BlindmodulationrecognitionalgorithmforMQAMsignals[J].JournalofElectronics&InformationTechnology, 2011, 33(2): 332-336. (inChinese)

[11]廖灿辉, 涂世龙, 万坚. 一种抗频偏的卫星幅相调制信号识别算法[J]. 电子与信息学报, 2014, 36(2): 346-352.

LIAOCanhui,TUShilong,WANJian.Ananti-frequency-offsetalgorithmformodulationrecognitionofsatelliteamplitude-phasemodulatedsignals[J].JournalofElectronics&InformationTechnology, 2014, 36(2): 346-352. (inChinese)

[12]靳晓艳, 周希元. 一种最大似然调制识别的快速算法[J]. 系统工程与电子技术, 2013, 35(3), 615-618.

JINXiaoyan,ZHOUXiyuan.Fastalgorithmformaximumlikelihoodmodulationclassification[J].SystemsEngineeringandElectronics, 2013, 35(3), 615-618. (inChinese)

[13]ShiQH,KarasawaY.Automaticmodulationidentificationbasedontheprobabilitydensityfunctionofsignalphase[J].IEEETransactionsonCommunications, 2012, 60(4): 1033-1044.

[14]谭晓波, 张杭, 朱德生. 基于星座图恢复的PSK信号调制方式盲识别[J]. 宇航学报, 2011, 32(6): 1386-1393.

TANXiaobo,ZHANGHang,ZHUDesheng.BlindmodulationrecognitionofPSKsignalsbasedonconstellationrecovery[J].JournalofAstronautics, 2011, 32(6): 1386-1393. (inChinese)

[15]程汉文, 吴乐南. 有频偏的星座图恢复和匹配[J]. 电路与系统学报, 2010, 15(1): 49-54.

CHENGHanwen,WULenan.Constellationrecoveryandmatchwithfrequencyoffset[J].JournalofCircuitsandSystems, 2010, 15(1): 49-54. (inChinese)

[16]WangY,SerpedinE,CiblatP.Optimalblindnonlinearleast-squarescarrierphaseandfrequencyoffsetestimationforgeneralQAMmodulations[J].IEEETransactionsWirelessCommunications, 2003, 2(5): 1040-1054.

[17]CiblatP,GhoghoM.BlindNLLScarrierfrequency-offsetestimationforQAM,PSK,andPAMmodulations:performanceatlowSNR[J].IEEETransactionsonCommunications, 2006, 54(10): 1725-1730.

[18]彭耿, 黄知涛, 陆凤波, 等. 中频通信信号信噪比的快速盲估计[J]. 电子与信息学报, 2010, 32(1): 102-106.

PENGGeng,HUANGZhitao,LUFengbo,etal.FastblindSNRestimationofIFcommunicationsignals[J].JournalofElectronics&InformationTechnology, 2010, 32(1): 102-106. (inChinese)

Constellation recovery and modulation recognition for multiple quadrature amplitude modulation signals

LU Shanshan1,2, WANG Wei1, WANG Guoyu1

(1.CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China;2.StateKeyLaboratoryofComplexElectromagneticEnvironmentEffectsonElectronicsandInformationSystem,NationalUniversityofDefenseTechnology,Changsha410073,China)

Abstract：Analgorithmformodulationrecognitionofmultiplequadratureamplitudemodulationsignalsbasedonconstellationrecoverywasproposed.Firstly,parametersofthecarrierfrequencyandsignaltonoiseratiowereestimatedfromitsspectrum.Accordingtothebaudrateandthesymboltiming,thebaudratesamplingwasfinished.Thenanon-data-aidedcarrierfrequencyoffsetestimationmethodwasusedtomitigatetheeffectoffrequencyoffsetandphaseoffsetinconstellationrecovery.Finally,themodulationtypewasrecognizedbytheaveragelikelihoodratiotestmethod.Simulationresultsdemonstratethattheproposedalgorithmhasabetterrecognitionperformancewhencomparingwiththeamplitude-basedmaximumlikelihoodalgorithm.

Keywords：modulationrecognition;offsetestimation;constellationdiagram;maximumlikelihood

doi:10.11887/j.cn.201603022

收稿日期：2015-05-08

基金项目：国家自然科学基金资助项目(61571451)

作者简介：陆珊珊(1986—)，男，安徽淮南人，博士研究生，E-mail：sslu2004@sina.com； 王伟(通信作者)，男，教授，博士，博士生导师，E-mail：13807319968@139.com

中图分类号：TN911.7

文献标志码：A

文章编号：1001-2486(2016)03-130-05

http://journal.nudt.edu.cn