在轨加注过程中组合体航天器动力学建模与分析*
2016-07-14杨雅君文援兰
杨雅君,廖 瑛,文援兰
(国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
在轨加注过程中组合体航天器动力学建模与分析*
杨雅君,廖瑛,文援兰
(国防科技大学 航天科学与工程学院, 湖南 长沙410073)
摘要:针对在轨加注过程中质量分布随时间变化的组合体航天器,研究动力学建模问题并对其动态特性进行分析。将航天器系统分为刚性组合体平台和贮箱内燃料两部分,贮箱内的燃料视为质量、外形和位置连续变化的质量块,将航天器系统抽象为一组有固定边界的变质量质点系;在推导出变质量质点系一般力学方程的基础上,通过对航天器结构进行一定限制消除方程中的反冲力和失调力矩,以组合体平台主轴作为参考坐标系,建立在轨加注过程中组合体动力学模型;该模型除了参数时变的特点外,与普通刚体动力学相比还含有阻尼项;基于李雅普诺夫稳定判据,对该时变动力学系统的动态特性进行分析。仿真计算展现了不同结构参数对姿态运动轨迹的影响,也证明了理论分析的正确性。
关键词:在轨加注;时变参数;变质量系统;航天器动力学;稳定性分析
在轨加注技术是空间在轨服务的重要组成部分,通过对在轨运行的航天器进行推进剂加注补给,不仅可以延长使用寿命、提高轨道机动能力,还为增加有效载荷比重和降低发射成本提供了可能,具有良好的经济效益和广泛的应用前景,因此备受各航天大国的重视。现有的在轨加注技术要求服务航天器与目标航天器进行空间对接,形成新的组合体后再将加注贮箱内的燃料经管路连续不断地传输到目标航天器贮箱中。
虽然在轨加注技术早已用于实践,但相关文献却并不多见,特别是在轨加注过程中的航天器动力学建模和分析,仅查阅到文献[1]和文献[2]有所涉及。文献[1]考虑转动惯量的时变效应,通过对角动量方程直接求微分得到姿态动力学方程,所得到的方程与描述刚体姿态运动的欧拉方程相比多出一项与转动惯量变化率有关的项。文献[2]将贮箱内的燃料视为外形变化的匀质刚体,详细推导了系统转动惯量随时间变化的公式,将计算得到的系统转动惯量直接代入到欧拉方程中建立姿态动力学模型。上述两篇文献并没有对系统的运动特性进行分析。加注过程中,燃料从加注贮箱转移到目标贮箱,服务航天器质量随之减少,目标航天器质量持续增加,可以借鉴变质量体系统的建模方法。文献[3]建立了考虑燃料消耗时质量和转动惯量随时间变化的飞艇的6自由度运动方程。文献[4]以固体火箭为背景,分析了有大量质量损耗时的自旋体姿态运动特性。文献[5]研究了在时变惯量矩和黏滞阻力影响下的非对称航天器的姿态运动,并对运动的混沌现象进行了深入分析。杨雅君等在文献[2]提出的简化条件基础上,对在轨加注过程中航天器系统的动力学建模和分析进行深入研究。
1力学原理
对于加注过程中的组合体航天器,由于燃料传输造成系统质量分布持续变化,航天工程中常用的单刚体或多刚体建模方法不再适用,有必要重新审视建模所基于的力学原理。考虑一组有固定边界的变质量质点系[6],如图1所示,R0为固连参考坐标系原点的绝对位置矢量,Ri为质点mi的绝对位置矢量,ri为质点mi相对参考坐标系原点O的位置矢量。因为质量分布随时间变化,系统质心位置也是时变的,因此体固连参考坐标系的原点选择在任意非系统质心的固定点上。
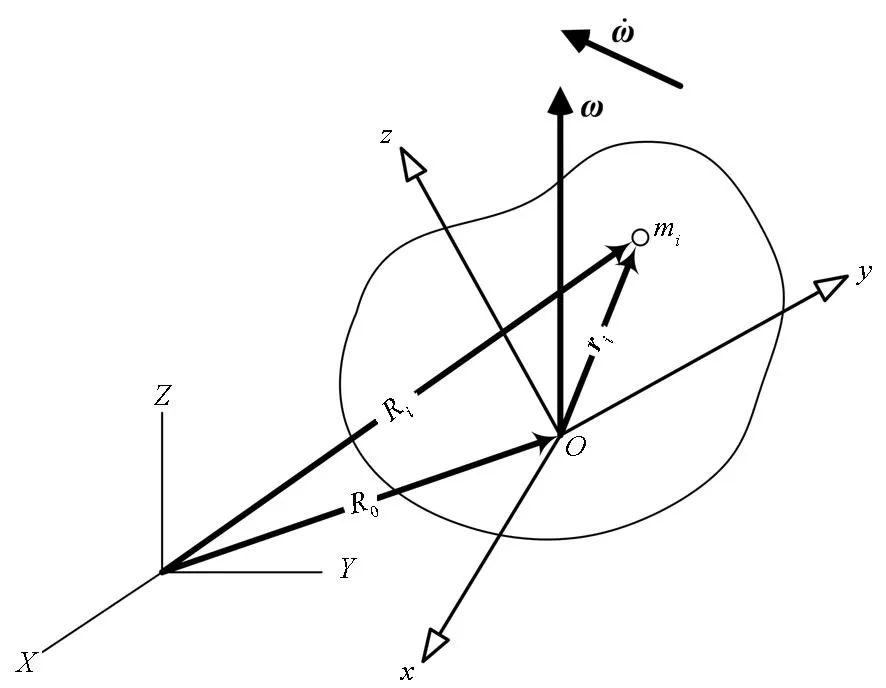
图1 边界固定的变质量质点系Fig.1 System of particles with varying mass andfixed boundary
在t时刻,系统相对参考坐标系原点O的角动量为:
(1)
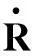
(2)
(3)
(4)
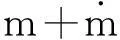
(5)
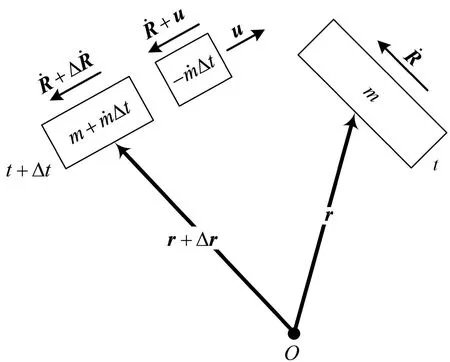
图2 质点m在t和t+Δt时刻角动量Fig.2 Angular momentum of element m at t and t+Δt
用式(5)减去式(2)并除以Δt,求Δt→0的极限并忽略高阶小量,得到系统角动量变化率为:
(6)
将式(6)代入式(4),得到质量变化时的力矩方程为:
(7)
质点绝对加速度的一般表达式为:
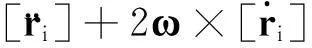
(8)
(9)
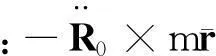
边界固定的变质量质点系的在外力作用下,瞬时质心的加速度和质量流的线动量会发生改变,外力方程为:
(10)
可见,对于变质量质点组成的系统,其力方程(10)和力矩方程(9)是相互耦合的。
2动力学模型与分析
2.1系统特点与假设
加注中的组合体航天器具有以下特点:通过刚性对接机构的连接,服务航天器壳体与目标航天器壳体之间没有相对运动,形成一个刚性组合平台;在液体管理装置的作用下贮箱内气-液完全分离,燃料被气液分离面和贮箱壁约束成规则的几何体;加注贮箱内的燃料通过管路向目标贮箱转移,各贮箱内燃料的形状和质量持续变化。因此,考虑将整个系统分成三个部分:刚性组合体平台(整个系统除去燃料的部分)、加注贮箱内的燃料、目标贮箱中的燃料。
①假设燃料为不可压缩流体;②参考当前三轴稳定航天器对接技术和文献[2]的模型,假设组合体平台的主轴系的x轴与对接轴重合,且加注贮箱和目标贮箱纵轴也与对接轴重合;③假设加注贮箱燃料出口处的法线方向与目标贮箱燃料入口处的法线方向同向且与对接轴平行;④假设燃料出口截面积与入口截面积相等。系统结构如图3所示。
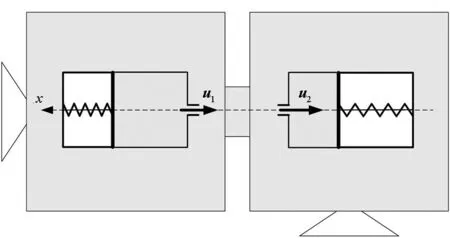
图3 组合体航天器结构Fig.3 Configuration of assembled spacecraft
2.2动力学模型
(11)
(12)
其中,系统总质量为:
m=Mb+m1+m2
(13)
系统质心位置及其速度、加速度分别为:
(14)
(15)
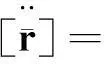
(16)
系统转动惯量为:
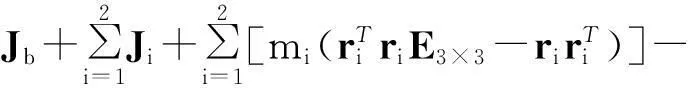
(17)
(18)
其中,m10和m20分别表示加注和目标贮箱内燃料的初始质量。 对于转动惯量,需要明确受约束燃料的几何形状,考虑贮箱为圆柱体,根据均质圆柱体转动惯量计算公式,贮箱内燃料的惯量矩为:
(19)
其中:i=1,2;R1和R2为贮箱底面半径;l1和l2为圆柱体母线长度。对于均质燃料,设密度为ρ,则母线长度随时间变化的公式为:
(20)
根据式(20)并考虑贮箱的安装方式,贮箱内燃料的质心位置及其变化率分别为:
(21)
(22)
其中,r10=[r100]T和r20=[r200]T分别为加注贮箱和目标贮箱内燃料的初始质心位置。
设参考坐标系O-xyz中组合体平台的惯量矩为Jb=diag(Jbx, Jby, Jbz),将式(19)~(22)代入式(12)~(17)中并展开,整理出状态方程形式的数学模型。
(23)
其中,
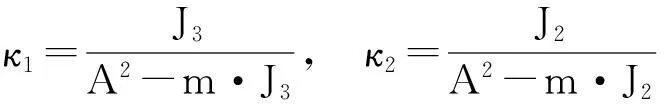
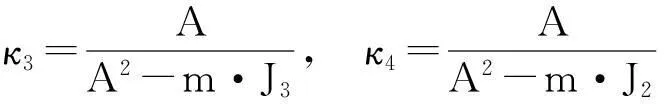
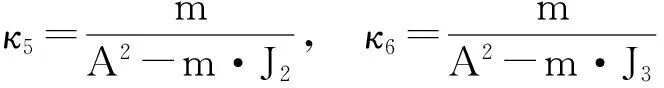
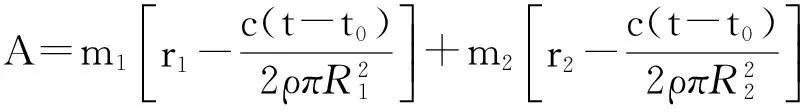
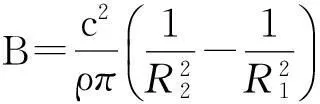
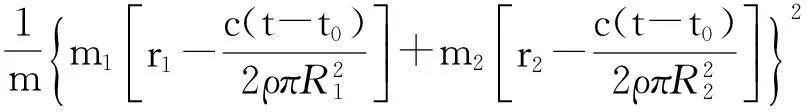
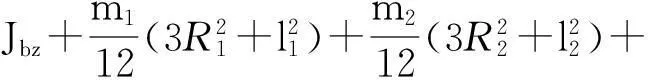
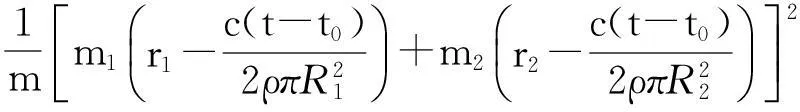
从式(23)可见,姿态变量ω=[ω1ω2ω3]T的变化不受线位移变量R=[RxRyRz]T的影响,可以单独对其进行研究。
2.3姿态自由运动分析
无外力作用情况下,加注过程中组合体的姿态动力学方程为:
(24)
其中,η1(t)=-(Jbz-Jby)/J1(t),
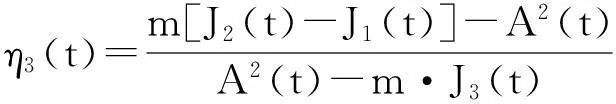
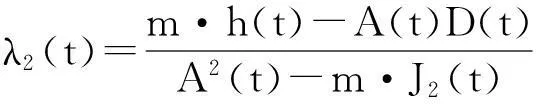
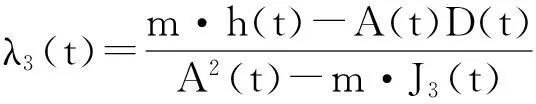
如果组合体质量分布相对x轴对称,即Jbz=Jby时,则η1(t)≡0,J(t)=J2(t)=J3(t),η(t)=η2(t)=-η3(t)和λ(t)=λ2(t)=λ3(t),且角速度ω1为常数,设Ω(t)=η(t)ω1,姿态动力学方程(24)具有线性时变系统的形式。
(25)
显然该系统具有一个平衡点[ω2ω3]T=[00]T,下面讨论这个线性时变系统(25)的运动特性。
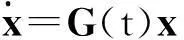
(26)
证明:略,参见文献[7]。
□
对于式(25)所示系统,设P(t)=I,根据式(26)构造Q(t)为:
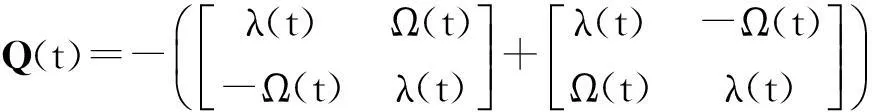
=-2λ(t)I
可见,当λ(t)<0, ∀t>t0时,Q(t)是连续的正定对称矩阵,此时ω2(t)和ω3(t)轨迹将指数收敛到0。当λ(t)>0时,ω2(t)和ω3(t)轨迹不确定,可能是周期变化或发散的。
通过分析可以明确,由于质量分布随时间改变,加注过程中的航天器姿态运动与刚体航天器姿态运动相比存在本质差异。自旋单刚体航天器在不受外力作用时,角速度轨迹呈周期变化,而质量分布时变航天器动力学方程中存在阻尼项λ(t),在时变阻尼项λ(t)的影响下角速度轨迹可以收敛到0,但也存在发散的可能性。
3仿真算例
通过两个仿真场景,展现不同贮箱安装位置对角速度轨迹的影响。仿真中设定的模型参数见表1。
以角速度ω(t0)=[0.1,0.141 4,0.141 4]T作为初值进行数值积分,得到角速度随时间变化轨迹如图4所示,同时也给出了时变阻尼系数的变化轨迹如图5所示。在场景1中,加注贮箱安装在x轴负半轴,目标贮箱安装在x轴正半轴,整个仿真时间内阻尼系数λ1(t)随时间连续变化但保持为负,此时ω1收敛到一个定值,ω2和ω3收敛到0。场景2与场景1贮箱安装方式相反,此时,阻尼系数λ1(t)保持为正,角速度轨迹振荡发散。

表1 仿真参数设置
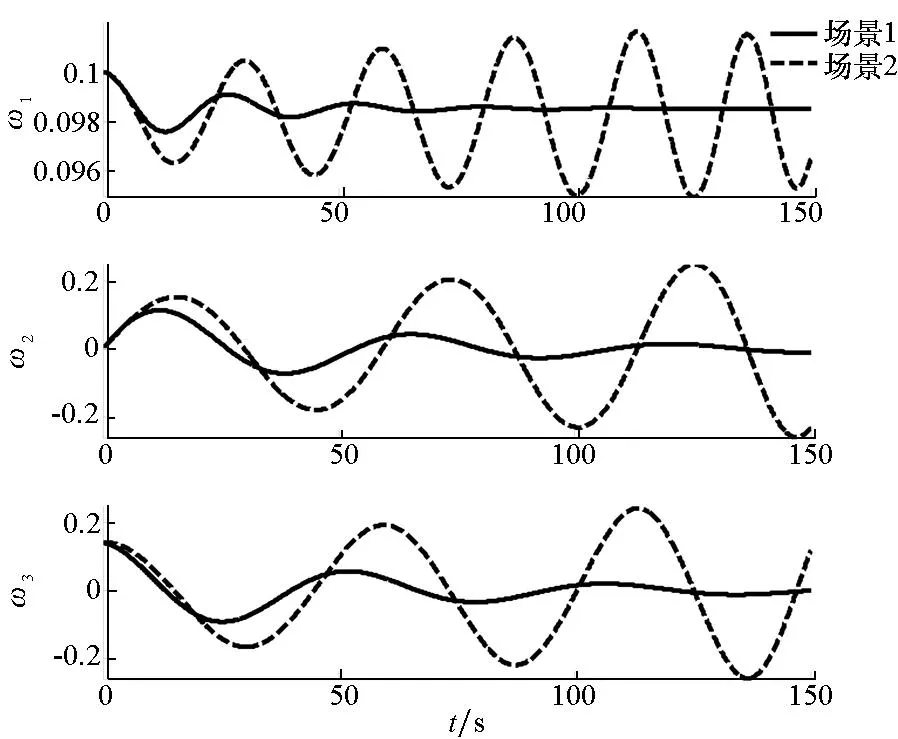
图4 姿态角速度时间历程Fig.4 History of angular rate
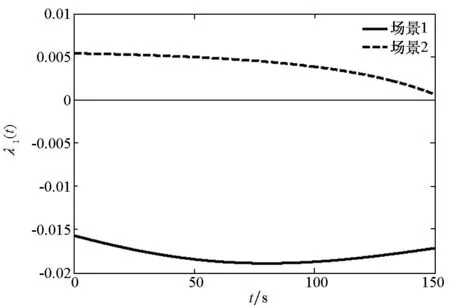
图5 阻尼系数λ1(t)时间历程Fig.5 History of damping coefficient λ1(t)
图6和图7分别为t=100s,ω1=0.01rad/s时,场景1和场景2的ω2-ω3流场图。从图6、图7可以清晰地看出,在场景1中ω2-ω3平面的原点为稳定焦点,而场景2中原点为非稳定焦点。
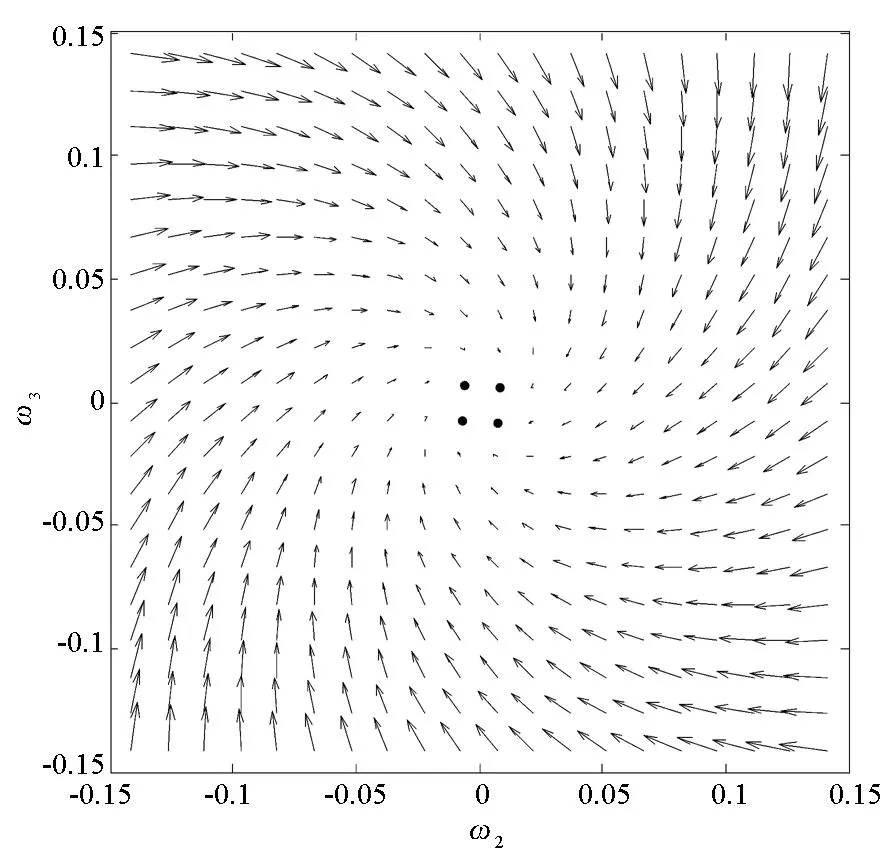
图6 场景1的流场图Fig.6 Map of flow field in scene 1
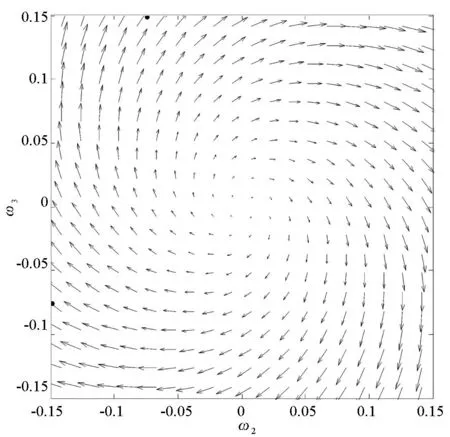
图7 场景2的流场图Fig.7 Map of flow field in scene 2
从以上仿真分析中可以看出,燃料传输涉及的参数会对航天器姿态的动态特性带来直接影
响,而且这种影响所造成的结果并不唯一,既可能使姿态角速度稳定收敛,也可能使角速度振荡发散。
4结论
基于变质量质点系一般力学原理建立了在轨加注过程中组合体航天器的动力学模型,利用该模型可实现对运动参数的数值计算,进而分析系统的动态特性。通过仿真分析可以看出,燃料传输对系统动态的影响是明显且复杂的,既可能使角速度稳定也可能使之发散。这为在轨加注航天器的结构和控制系统设计提供参考为加注过程中的控制系统设计奠定了基础。
参考文献(References)[1]王大奎, 高云峰. 卫星在轨加注姿态变化研究[C]//北京力学会第17届学术年会论文集, 2011: 2-3
WANGDakui,GAOYunfeng.Researchonsatelliteattitudemovementduringon-orbitrefueling[C]//ProceedingsofBeijingSocietyofTheoreticalandAppliedMechanicConference,Beijing, 2011: 2-3 .(inChinese)
[2]张龙, 段广仁, 张永安. 在轨加注航天器的姿态动力学模型[J]. 哈尔滨工业大学学报, 2011, 43(5): 20-24.
ZHANGLong,DUANGuangren,ZHANGYongan.Attitudedynamicsmodelofon-orbitrefuelingspacecrafts[J].JournalofHarbinInstituteofTechnology, 2011, 43(5): 20-24. (inChinese)
[3]WaishekJ,DoganA,BestaouiY.Investigationintothetimevaryingmasseffectonairshipdynamicsresponse[C]//Proceedingsof47thAIAAAerospaceSciencesMeetingIncludingtheNewHorizonsForumandAerospaceExposition, 2009.
[4]EkeFO,MaoTC,MorrisMJ.Freeattitudemotionsofaspinningbodywithsubstantialmassloss[J].JournalofAppliedMechanics, 2004, 71(2): 190-194.
[5]IarreaM,LancharesV,RothosVM,etal.Chaoticrotationsofanasymmetricbodywithtime-dependentmomentsofinertiaandviscousdrag[J].InternationalJournalofBifurcationandChaos, 2003, 13(2): 393-409.
[6]ThomsonWT.Introductiontospacedynamics[M].USA:DoverPublications, 1986.
[7]KhalilHK. 非线性系统[M]. 北京: 电子工业出版社, 2011.
KhalilHK.Nonlinearsystem[M].Beijing:PublishingHouseofElectronicsIndustry, 2011.(inChinese)
Dynamics modeling and analysis of on-orbit refueling assembled spacecraft
YANG Yajun, LIAO Ying, WEN Yuanlan
(CollegeofAerospaceScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)
Abstract:Aresearchwaspresentedtosolvetheproblemofdynamicsmodelingandcharacteristicsanalysisinthecaseofthemassdistributionofthespacecraftchangesobviouslyduringtheon-orbitpropellantrefuelingprocess.Thevariable-massvehiclewasconsideredtoconsistoftwoparts:arigidplatformandtheliquidpropellantconfinedintanks.Theliquidintankswasregardedasafinitenumberoflumpedmasseswithtime-varyingmass,configurationandposition,sothat,theactualphysicscouldbeabstractedasasetofvariablemassparticleswithfixedborder.Then,thedynamicsmodelofrefuelingspacecraftwasestablishedbyusingthegeneralequationsofmass-varyingparticlesset.Basedonsomereasonableassumptionsaboutthestructureofvehicle,themisalignmentmomentandthereactiveforcewereeliminatedfromequations.Itisremarkablethattheestablishedmodelincludetime-varyingparametersanddampingterms.Besides,thedynamicscharacteristicsofthemodelwereanalyzedbyusingtheLyapunov′sstabilitycriterion.Simulationresultsdemonstratethatthedifferencestructureofthevehicleeffectthestatetrajectoriesdramatically,andprovethattheoreticanalysisiscorrect.
Keywords:on-orbitrefueling;time-varyingparameters;variablemasssystem;spacecraftdynamics;stabilityanalysis
doi:10.11887/j.cn.201603015
收稿日期:2015-04-08
基金项目:上海航天科技创新基金资助项目(SAST201251)
作者简介:杨雅君(1987—),男,云南勐腊人,博士研究生,E-mail:yajunsand@163.com; 廖瑛(通信作者),女,教授,博士,博士生导师,E-mail:liaoying1104@163.com
中图分类号:V443.5
文献标志码:A
文章编号:1001-2486(2016)03-088-06
http://journal.nudt.edu.cn
