学了就要用*——高中生也能解平面几何题

●崔志荣

(安丰中学　江苏东台　224221)



学了就要用*
——高中生也能解平面几何题

●崔志荣

(安丰中学江苏东台224221)

摘要：数学教学，要让学生明白知识、方法的内涵，知道学习它的意义.不仅如此，还要有合理的应用导向，要突破问题的界限，培养学生的应用迁移能力，发挥所学知识、方法的工具性作用，把它们充分运用到所能解决的问题中去.让学生学以致用，这应是我们追求的教学境界.

关键词：学以致用;教育价值;问题界限

1方法启示

图1

(《学数学》“数学贴吧”2016年第1季探究问题)

笔者为什么会关注到这道平面几何题呢？因为这道题的供题人是单墫教授，而且这道题的问题有点特别，“不用三角函数”证明结论，意思是用三角函数证明，难度可能不大，但另一层意思是，不一定非要用综合法证明该题，还可以用其他方法来研究这道平面几何题.

受此启发，笔者想到不参加竞赛的高中生平面几何知识遗忘比较严重，对较难的平面几何题，很不适应用定理结合题目条件推理证明结论，他们能否运用高中所学习的知识方法去研究这道平面几何题呢？

2学以致用

带着上述思考，笔者回顾了一下高中数学内容，拟站在高中生的角度，分析这道几何题.首先高中生会不会用分析法梳理需要证明的结论呢？

条件：

结论：

即要证

即证

2.1解析法

解析几何的本质是用代数的方法解决几何问题，它是高中数学的重点内容，如让高中生做这道平面几何题，应想到解析法.

图2

证法1如图2，以BC所在直线为x轴、AD所在直线为y轴建立直角坐标系.设B(m,0)，C(n,0)，A(0,h)，其中m<0,n>0,h>0，则AD=h.因为

所以直线BH的方程为

令x=0，得

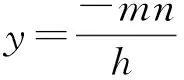
即

从而

又由点B,C的坐标可得以BC为直径的⊙M方程为

(x-m)(x-n)+y2=0，

令x=0，得

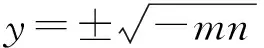
即

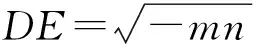
于是

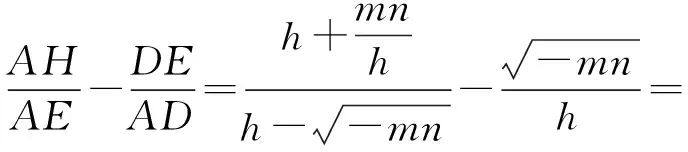
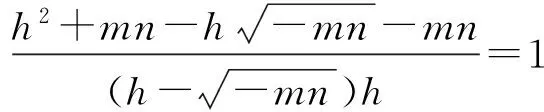
从上述解题过程可以发现，这道平面几何题用解析法比较容易解决，关键是学生要有较强的建系意识.对于一个具体的平面几何题，解析法不一定非常简单，但它是我们要思考的方法之一，比较综合法与解析法，看看哪个方法更简便易行.

2.2三角函数法

单教授提出不用三角函数证明，说明由该题的条件想到三角函数不难，由于题中垂直条件较多，只要在直角三角形中运用三角函数知识，选择几个基本量表示结论中的相关量即可.其实，需用的三角函数知识并不多，高中生与初中生一样能完成，关键是学生是否会往这一方向走？

图3

证法2如图3，设AD=h，则

联结BE,CE,因为AD⊥BC，且BC为⊙M的直径，所以

且∠CHD=∠ABC，于是

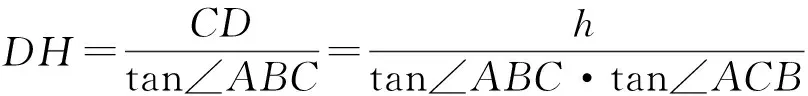
上述过程，所选择的基本量是AD，tan∠ABC,tan∠ACB,以此表示结论中的4个长度AD,AE,AH,DE.为什么把AD,tan∠ABC,tan∠ACB作为本题的基本量呢？因为这3个量能够控制整个图形的形状，其中AD具有桥梁作用，它连接Rt△ABD和Rt△ACD.

2.3向量法

向量集数形于一身，它是解决几何问题的一个工具，也是高中数学的重点内容，可让高中生用向量法证明这道平面几何题.若用向量的坐标运算求解，则与解析法相差无异，用向量的非坐标运算，怎么证明呢？

AD·AH-AE·ED-AD·AE=0，

转化为向量的数量积运算即可.如图3，因为

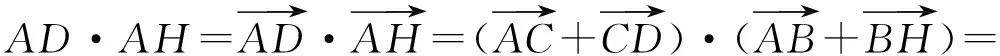
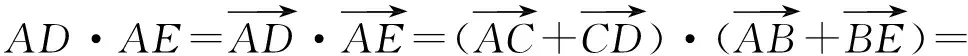
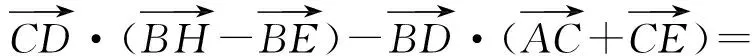
2.4分析法

分析法是寻找结论成立原因的一种推理方法，上文已初步运用了分析法，实际上，可以完全用分析法证明该题的结论.

AD·AH-AE·ED=AD·AE，

⟸

AP·AC=AE(AD+DE)，

⟸

AP·AC=(AD-DE)·(AD+DE)，

⟸

AP·AC=AD2-DE2，

⟸

AP·AC=AC2-CD2-BD·CD，

⟸

CD2+BD·CD=AC2-AP·AC，

⟸

CD·BC=AC·PC.

而由△ACD与△BCP相似，可得CD·BC=AC·PC成立，故原命题结论成立.

高中生已详细学习了分析法的原理，面对这道平面几何题，容易想到分析法.当然，上述证明过程有一个关键不易想到，即把AE换为AD-DE转化为平方运算.

3学以致用的2点思考

单教授提供的这道平面几何题，可用高中数学相关知识求解.当然，不是每一道平面几何题，都能用上述方法顺利完成，但对任何一道平面几何题，我们都应有上述几种分析思路，从中选择合适的方法求解.这让笔者重新审视了高中数学的相关内容，再理解它们的本质内涵、领悟它们的教育价值，反思这些内容在数学教学中?如何把根留住(详见文献[1]),如何让学生学以致用？就此谈2点个人看法，不足之处，望批评指正.

3.1提高教育价值取向，让学生学以致用

如果让高中生完成单教授提供的那道平面几何题，他们能想到上述4种证明方法吗？我们先看下面这个案例，答案自然知晓.

图4

例2如图4，在梯形ABCD中，B，D关于对角线AC对称的点分别是B′,D′，A,C关于对角线BD对称的点分别是A′,C′，证明：四边形A′B′C′D′是梯形.

(2013年全国高中数学联赛江苏赛区初赛测试卷试题)

笔者在文献[2]中提到，笔者所在市(县级市)有3所四星级高中和2所三星级高中，四星级高中参赛人数比例约80%，三星级高中参赛人数比例约5%，全市约2 500人参赛.阅卷统计发现：1)约60%的考生试卷空白；2)约35%的考生运用综合法完成，但完全正确的人数只有27人，约占总数的1%；3)约5%的考生选择了解析法.

上述案例说明，高中生面对平面几何题的主要思路仍然是综合法，大多数学生不能把高中所学知识用到平面几何题的分析中去.事实上，这道联赛题用解析法容易完成(解析法详见文献[1]).因此，有必要反思一下高中数学相关内容的教育价值.

对于解析几何，除了要让学生掌握直线与圆、圆锥曲线等解析知识外，还要让学生领悟解析思想，增强建系意识，让学生学以致用，把解析知识切实用到解决平面几何问题中去，而不仅仅是让学生会做“解几题”，即解决坐标系下的直线与圆以及圆锥曲线问题.

向量既是知识，又是解决实际问题的工具，我们只教给学生向量知识，让他们做所谓的向量题，太狭隘了！应发挥它解决平面几何、物理等相关问题的作用，体现学习向量的价值.

三角函数源于三角形，并形成了一个重要的数学分支.作为中学数学，我们不能只让学生做三角函数题，还要加强它的应用，也不能只用于解三角形，很多复杂的几何图形都是以三角形为单元，要让学生分解出这些图形中的三角形，再运用三角函数知识解决问题.

分析法是一种方法，是一种思维，不能当成知识教给学生，也不要指望学习分析法时，教几道例题，学生练习几道题，他们就能掌握分析法.只有在平时解题教学中多运用，学生的逆向思维能力才能得以提升，碰到具体问题时，才能用分析法完成.请看下面的例3，并没有指明用什么方法证明，但可以用分析法迅速解答.

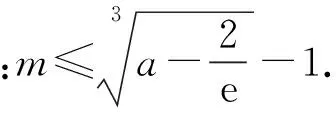
(2015年广东省数学高考试题)

分析由f′(x)=(1+x)2ex=0，得

xP=-1，

因此

yP=2e-1-a，

于是

kOP=a-2e-1.

因为点M的坐标为(m,n)，所以函数f(x)在点M处的切线斜率为

k=(1+m)2em，

于是

a-2e-1=(1+m)2em.

至此，经验不丰富的学生将无法继续推算，但若善于运用分析法，则能顺利完成.

问题即要证(m+1)3≤a-2e-1，即证

(m+1)3≤(1+m)2em，

即

em≥1+m，于是构造函数g(x)=ex-x-1，证明g(x)≥0即可.

数学课堂要凸显教育价值，教学就要加强所学知识的应用价值，让学生学有所用，用到解决具体问题中去，这应是教学要追求的境界.

3.2突破问题界限，加强知识方法的迁移

对于现行的数学考试，笔者有点想法提出来与广大读者商榷.笔者认为考试题型太过于固定，问题的界限太明显.比如数学高考解析几何的考查，通常有一道大题，一般是坐标系下的椭圆(或圆、抛物线、双曲线)问题，所提问题过于死板，或者让学生求一些几何量、或者证明一些几何性质，试题的封闭性很强，就是按照考试说明的要求，考查学生的解析几何知识.当然，笔者不是反对这种考查形式，它确实考查了学生的思维能力、运算能力、方法的选择能力等，可以突破问题的界限，增加一点发散性.笔者对上文单教授给出的题目改编如下:

高中数学考查平面几何题，行不行？笔者认为可以，我们的目的不是考查学生的几何推理能力，而是高中所学知识的迁移运用，让学生学有所用.这道改编题让学生分析解题思路，类似于课题研究，要找准课题研究的方向.它能考查学生知识的综合运用能力和迁移能力，只有深刻理解所学知识的内涵，才能完成.当然，不是说所有考题，都要以这种形式命题，但笔者认为现行的数学考试，要减少题量、减少封闭性试题；要大胆突破界限，增加研究型、开放性试题，加强学生数学思想方法的考查，让学生把所学知识灵活运用到解决不同类型问题中去.

我们常讲，要让学生构建知识体系.构建知识体系，谈何容易？不突破问题的界限，让学生思考知识的关联，只让学生解决封闭性试题，着重“术”的研究，学生的理解终究不会深刻，很难做到知识迁移，学有所用.

4结束语

把知识方法教给学生容易，但要让学生学了就能用，不容易！你得让学生明白知识方法的内涵，让学生知道学习它的意义，不仅如此，还要有合理的应用导向，逐步熏陶学生的应用意识，才能提高学生应用的迁移能力，真正做到学以致用.

参考文献

[1]曹凤山.数学教学：把根留住——2015年浙江省高考数学试题解读[J].中学教研(数学)，2015(8)：3-6.

[2]崔志荣,薛宗华.落实解析几何教学的四个环节——由一道联赛题引起的教学思考[J].数学通讯，2013(10)：16-18.

[3]罗增儒.什么是“数学题”——商榷“数学题”的流行误解[J].数学教学，2015(12)：1-6.

修订日期：*收文日期：2016-04-09；2016-05-10

基金项目：江苏省教育科学“十二五”规划2015年度重点自筹课题(B-b/2015/01/088)

作者简介：崔志荣(1978-)，男，江苏东台人，中学一级教师.研究方向：数学教育.

中图分类号：O12

文献标识码：A

文章编号：1003-6407(2016)07-26-04