平面向量基本定理与高等数学的联系及教学思考*

●张健　　朱哲

(浙江师范大学教师教育学院　浙江金华　321004)



平面向量基本定理与高等数学的联系及教学思考*

●张健朱哲

(浙江师范大学教师教育学院浙江金华321004)

摘要：平面向量基本定理与高等数学之间具有密切的联系，在数学教学的过程中应该关注到这种联系，渗透高观点.文章主要讨论了平面向量基本定理与高等代数和高等几何的联系，进而产生了一些教学思考.

关键词：平面向量基本定理；高等数学；教学思考

人教A版《数学4(必修)》中专门编排了“平面向量的基本定理及坐标表示”这一内容供高中学生学习.平面向量基本定理是高中数学重要的内容，它基于平面向量的线性运算对平面内向量的构成进行探讨，其中蕴含的“基底”思想体现了“化归”的数学思想方法，它也是向量坐标表示的依据.另外，平面向量基本定理在处理平面几何等问题中也具有非常强大的力量.

德国数学家克莱因在《高观点下的初等数学》中认为教师应具备较高的数学观点.理由是:观点越高，事物越显得简单[1].在这一思想指导下，笔者试图采用高观点去寻找平面向量基本定理与高等数学的联系，并由此引发一些教学思考，希望可以对中学数学教学产生一些有益的启示.

1平面向量基本定理与高等数学的联系

向量具有丰富的实际背景：几何背景、物理背景等等，在实际应用中十分广泛.平面向量是从实际背景抽象得到的数学对象，运算的引入使得平面向量具有强大的力量.平面向量基本定理刻画的则是平面内向量的构成，它与高等数学具有密切的联系，下面从高等代数和高等几何2个角度来讨论平面向量基本定理与高等数学之间的联系.

1.1与高等代数的联系

教科书中的平面向量基本定理表述如下：如果e1,e2是同一平面内的2个不共线向量，那么对于这一平面内的任意向量a，有且只有1对实数λ1,λ2，使得a=λ1e1+λ2e2,其中e1,e2称为表示这一平面内所有向量的一组基底[2].从高等代数中线性空间的角度来看，这一定理实则是一种特例.

线性空间简单地说就是一个具有某种代数结构的集合.给定一个数域P，设V是一个非空集合，在集合V中的元素之间定义“加法”运算，在集合V和数域P之间定义“数量乘法”运算，并且2种运算满足一系列的规则，这样V就称为数域P上的线性空间[3].在线性空间中可以引入线性相关和线性无关的概念来刻画元素之间的关系，还可以按照维数对线性空间进行分类.在有限维的线性空间中可以定义基的概念：在n维线性空间V中，n个线性无关的向量ε1，ε2，…，εn称为一组基[3].从这个定义可以得到一个结论，它与我们的分析紧密相关，我们把它作为本文的定理1：

定理1对于n维线性空间V中任一向量α，α都可以被基ε1，ε2，…，εn线性表出，即α=a1ε1+a2ε2+…+anεn，并且系数a1，a2，…，an被向量α和基ε1,ε2,…,εn唯一确定[3].

我们将平面内所有向量构成的集合记为W，那么W按照向量的加法运算和向量的数乘运算构成一个R上的2维线性空间.在这样的观点下，平面内2个不共线的向量e1,e2是线性无关的，因此它们构成W的一组基.于是，平面向量基本定理就可以看成是定理1的推论，重新叙述如下：

推论1如果e1,e2是W的一组基，那么对于W中任一向量α，α都可以被基e1,e2线性表出，即α=a1e1+a2e2，并且系数a1，a2是唯一的.

将推论1与教科书中的平面向量基本定理进行对比就可以发现：推论1其实就是平面向量基本定理的实质.如果从更一般的角度去看，定理1才是平面向量基本定理的本质，而平面向量基本定理仅仅是定理1在非常特殊的条件下的推论.平面向量基本定理也可以视作是高等定理的一种“下放”，教科书对定理进行了一些“包装”，使其更易于被学生理解.比如教科书中略去了集合、线性表出等概念，结合平面向量的几何表示试图从几何直观的角度理解平面向量基本定理的内容.

定理1中的系数a1，a2，…，an被称为向量α在基ε1，ε2，…,εn下的坐标，这是抽象意义上的坐标概念.从这个角度来看，平面向量基本定理表达式中的系数λ1，λ2也可以被理解为向量α在基e1，e2下的“坐标”.因而，教科书中涉及到的“正交分解”和“坐标表示”实质是在上述2维线性空间W中选择了一组特殊的基(标准正交基)，在这组基下对平面向量进行坐标表示.

1.2与高等几何的联系

平面向量本身具有丰富的几何背景，平面向量基本定理在平面几何当中也有许多运用，这引导我们从直观的角度去寻找平面向量基本定理与高等数学的联系.高等几何中的仿射坐标系给我们提供了新的角度.

图1　　　　　图2

这说明了:平面向量基本定理表达式中的系数的几何意义就是仿射坐标，相对于高等代数从抽象意义上的坐标概念来解释其中的系数，这里的几何意义更为具体、直观.平面直角坐标系是一种特殊的仿射坐标系，从系数的几何意义来看，教科书中的“平面向量的坐标表示”其实就是平面向量在特殊的仿射坐标系下的仿射坐标(“基底”的选取要对应起来).

教科书中有这么一段提示语：“同一平面可以有不同的基底，就像平面上可选取不同的坐标系一样.”[2]现在，我们对这句话有了更加丰富的理解.

2平面向量基本定理的教学思考

平面向量基本定理与高等数学的联系十分密切，在教学设计的过程中应该看到这些联系，站在更高的观点和更广的视野去思考平面向量基本定理的教学，这将有助于加深对平面向量基本定理的理解并拓宽教学思路，在教学中渗透高观点.

2.1平面向量的“分解”与“合成”

在教学过程中，我们可以从“分解”与“合成”这2个角度对平面向量基本定理进行解读和反思，这可以帮助学生加深对这一定理的理解.教科书侧重的是从“分解”的角度来解读定理，如在探究定理的过程中指出“当e1,e2确定后，任意一个向量都可以由这2个向量量化，这为我们研究问题带来极大的方便.”[2]平面内的向量被归结为不共线的向量e1,e2，这体现了“化归”的思想.根据平面向量基本定理，我们可以对平面内的任意一个向量进行分解.

例1如图3，a和b是平面内2个向量，e1,e2和e3,e4是2组基底，通过作图分解向量：

1)分别在2组基底e1,e2和e3,e4下分解a；

2)在基底e1,e2下分别分解向量a和b.

图3

学生通过作图操作对平面向量的分解进行体验，为之后学习“平面向量的正交分解”作好铺垫.我们还可以从“合成”的角度来启发学生的思考.

例2e1,e2是平面内2个不共线的向量，对于任意实数λ1,λ2，按照λ1e1+λ2e2组合是否可以得到整个平面内的所有向量？用集合的语言描述就是集合{a|a=λ1e1+λ2e2,其中λ1,λ2∈R}与{a|a是平面内的向量}是否相等？

这个问题可以引发学生对于平面内向量的构成进行更为深入的思考，进一步拓宽视野.

2.2平面向量基本定理与平面直角坐标系

平面向量基本定理表达式中的系数具有明确的几何意义，即仿射坐标，这体现了平面向量基本定理与坐标系之间的联系.在学习完平面向量的正交分解及坐标表示之后，从平面向量的角度去反思平面直角坐标系，可以加深对平面直角坐标系的理解.

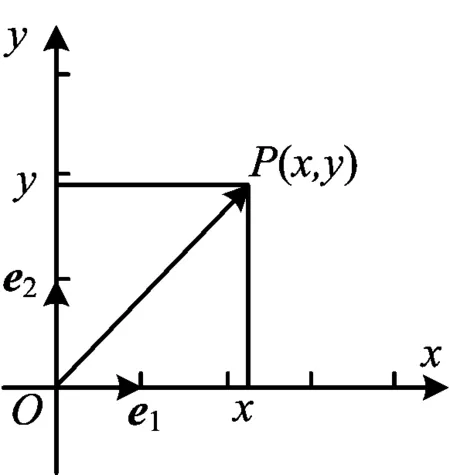
图4

这个例子说明了平面直角坐标系内点的坐标可以看成是由平面向量基本定理所确定，可以帮助学生更深入地认识平面直角坐标系.

2.3平面向量基本定理与平面向量共线的条件

教材中平面向量共线的条件b=λa可以看成是平面向量基本定理的一维情形.在学习完平面向量基本定理之后，可以引导学生借助平面向量基本定理去反思平面向量共线的条件.

例4在平面向量基本定理的表达式a=λ1e1+λ2e2中，如果将向量a限定在e1方向上，那么λ2=0.于是，式子a=λ1e1+λ2e2就变成a=λ1e1(其中e1≠0)，这即是平面向量共线的条件.

例5如图5,如果a是直线上的一个非零向量，那么对于直线上的任意向量b，b与a共线.根据平面向量共线的条件，有且只有1个实数λ，使得b=λa，其中a可以看成是表示这一直线上所有向量的一个基底.

图5　　　　　　图6

这2个例子将平面向量基本定理与平面向量共线的条件联系起来，使学生对平面向量共线的条件产生新的认识.更进一步，我们还可以将它们与数轴联系起来，从而更深刻地认识数轴.

在教学过程中，将平面向量基本定理与平面直角坐标系、数轴、平面向量共线的条件等知识联系在一起，可以让学生经历从新的角度去理解旧知识的学习过程，充分感受数学知识之间的联系.

高中数学不仅仅要为学生提供扎实的数学知识和技能，还要为学生进入大学学习高等数学打下基础.这要求教师要用更长远的眼光来进行教学，在教学中不仅仅要重视知识的来源和产生过程，还要关注知识的发展和延伸，为今后进一步学习数学积累材料.平面向量基本定理体现的“基底”思想在高中数学学习过程中是第一次出现，在高中数学中具有重要的地位，而从长远来看它则为高等数学的学习提供了初等的例子.因此，在教学该定理的过程中不仅仅要重视定理的探究过程，还要关注该定理与高等数学之间的联系，启发学生进行更深入地思考.

高中数学与高等数学之间具有密切的联系，数学教师不应该仅仅停留在初等数学层次去进行教学，而应该用更高的观点去看待高中的数学知识，善用高观点把握和理解教材，从而在更加广阔的视野中理解高中数学，并“居高临下”地进行教学.

参考文献

[1]吴大任.博洽内容独特风格——介绍克莱因:高观点下的初等数学[J].数学通报,1989(6):17-20.

[2]人民教育出版社课程教材研究所中学数学课程教材研究中心.普通高中课程标准实验教科书《数学4(必修)》[M].北京:人民教育出版社,2007.

[3]王萼芳,石生明.高等代数[M].3版.北京:高等教育出版社,2003.

[4]李宏基.斜坐标系之再探秘[J].上海中学数学,2009(11):33-35.

[5]梅向明,刘增贤,王汇淳,等.高等几何[M].3版.北京：高等教育出版社,2008.

修订日期：*收文日期：2016-03-14；2016-04-28

作者简介：张健(1993-)，男，浙江温州人，硕士研究生.研究方向：数学教育.

中图分类号：O123.1

文献标识码：A

文章编号：1003-6407(2016)07-30-03