问题引领式数学生态课堂的构想——以“几何概型”概念教学为例

魏有莲

（三明市第一中学，福建三明365001）



问题引领式数学生态课堂的构想
——以“几何概型”概念教学为例

魏有莲

（三明市第一中学，福建三明365001）

摘要：问题引领式数学生态课堂将数学学习内容转化为问题，以问题驱动学生主动学习和建构知识。现以“几何概型”概念教学为例，将生态课堂的流程从“领受、领悟、提升”三个阶段拓展为：创设情境，提出问题；教师引领，深化问题；自主学习，探究问题；合作研讨，解决问题；领悟新知，应用问题；升华知识，拓展问题六个环节，数学生态课堂教学更加具有操作性.

关键词：数学教学；问题引领；生态课堂

一、问题引领式数学生态课堂的基本含义

问题引领式数学生态课堂，是以教师引导为前提，以问题研究为载体，以自主学习为主线，让学生终生受益为目的，实现教学与学生发展相统一的课堂。这种课堂通过教师、学生、教学环境之间的对话和互动，教学关注点由认知领域走向生命领域。它有四个特点：

1.开放性。在问题引领下，数学课堂从封闭走向开放，系统内外各要素彼此相互联系，通过信息的流动、交换和解读，保证学生能够同化新知识，建立起新旧知识之间的联系。

2.共生性。学生在探究问题的过程中，通过交流、互动、质疑、争论等环节一起建构数学知识，实现共同发展。同时课堂精彩的动态生成也能促进教师的专业成长。

3.多样性。数学生态课堂系统与自然界生态系统相似，课堂是动态生成的，教学方法和评价方式是多样的，学生的表现是多姿多彩的。

4.可持续性。问题引领式数学生态课堂，在传授数学知识的同时，特别注意让学生掌握学习方法，养成主动学习和探究的习惯，为将来可持续发展奠基。

二、问题引领式数学生态课堂的初步构想

“生态课堂的宗旨是一切为了学生，学生在教师的引导下自由开放地独立自主地学习。生态课堂的流程可分为‘领受、领悟、提升’三个阶段”。领受：教师提出问题，学生弄清问题含义，接受学习任务。领悟：通过对问题的探究和讨论，学生解决问题，领会新知识，生成新知识。提升：对新知识应用和拓展，思维能力和创新精神得到发挥和张扬，实现课堂教学的生命价值。

1.创设情境，提出问题。有效创设情境，让学生发现问题，并对问题有强烈的兴趣，从而进入“心求通而未得”“口欲言而未能”的悱愤境界，激发起极大的求知欲。

情境1：小张用做游戏的方式确定周末是否去看电影，他随机地向圆盘投掷飞镖，飞镖落点位于小圆之内才能去看电影，小圆半径为大圆半径的二分之一，则小张周末去看电影的概率是多少？

图1

问题1：请同学们解答，并说明解答依据。

学生活动：充分讨论之后，大部分学生认为这问题的概率为“小圆面积与大圆面积之比”，但找不到计算的依据。

通过情境1引入课题，激发学生求知的原动力，问题用经验可以解决，但没有理论依据，让学生进入悱愤境界，对问题思考由感性深入到理性。

2.教师引领，深化问题。在教师引领下，以问题为起点，将学生兴趣问题进行深入分析，挖掘本质，深化含义。

问题2：请同学们回顾求随机事件概率的方法及古典概型的特点？

学生活动：一组学生上台书写计算随机事件概率的方法，另一组学生口头回答古典概型的特点。

通过复习已有的概率知识，为深入探究情境1问题建立最近发展区，提供研究问题的切入点，让学生顺利地领受学习任务。

3.自主学习，探究问题。放手让学生自主探究，教师将要学习的对象（数学内容）在最近发展区继续用问题形式展开，引导学生找到解决问题的通道，初步解决问题，完成对学习内容的初浅感悟。

问题3:研究一个概率问题的切入点是什么？

生：研究一个概率问题的切入点是分析基本事件、指定事件及其特点。

师：请同学们认真思考和分析情境1中概率问题的基本事件、指定事件及其特点。

生：情境1中基本事件是“飞镖落点在小圆之内”，每一个基本事件的发生是等可能的，基本事件的总数A和指定事件中所含基本事件的总数Ω都是无限的。

师：能用古典概型的概率公式计算这个概率吗？这是古典概型吗？

生：不能，因为出现了“无限比无限”的情况。这个问题不是古典概型。

设计意图：以概率问题的“基本事件”为切入口，对情境1深入分析，发现它仍是一个等可能模型，但A和Ω都是无限个，无法用数值表示，形成了新的认知冲突。

问题4：这是一种新的概率模型，能不能找到它的概率计算公式？

学生活动：根据情境1中问题的概率特点，类比古典概型，让学生找到解决问题的方法。

师：请同学们分析情境1中问题与古典概型的异同？

生：相同点“基本事件都是等可能的”，不同点“A 和Ω从有限变成了无限”。

师：既然有相似之处，能不能将古典概型的概率公式做一些修正，找到一个新的计算公式呢？

生：情境1中问题的基本事件和指定事件都发生在某一区域中，基本事件在区域内发生是等可能的，因此，可以用小圆面积来度量基本事件的总数A，用大圆面积来度量指定事件所含基本事件的总数Ω。这两个面积之比就是情境1中问题的概率。

因情境1问题是等可能事件，让学生发现可以用区域面积表示基本事件的总数，找到用几何图形面积之比计算概率的通道。

问题5：请同学们探索情境2和情境3中问题的概率的计算方法。

情境2：在区间[-2,3]上随机选取一个数X,则X不大于1的概率是多少？

情境3：一立方体空房间，边长为3米，地面的一个墙角落装有捕蝇器（大小忽略不计），可捕捉距离其2米空间内的苍蝇，若一只苍蝇在房间内盘旋，则它被捕捉的概率是多少？

学生活动：参照情境1思路，进行思维迁移，找到问题答案，并说明相应理由。

情境2、情境3中的问题可分别用长度之比和体积之比计算概率，让学生发现有一类事件的概率只与构成事件区域的长度、面积或体积成比例。这是一种新的概率模型。

4.合作研讨，解决问题。通过学习小组内的合作研讨，小组间的成果共享受，全面解决问题，达到对所学新知识比较全面、深入的理解，进而内化新知识，完成意义建构。

问题6：分析上述三个情境中问题的共同特点，总结出新的概率模型的概念、特点和概率计算公式。

学生活动：在教师的引导下，学习小组集中个人和集体智慧，经过组内分析、研讨、归纳，组间交流、争辩、总结，得到如下结论：

（1）如果每个事件发生的概率只与构成事件区域的长度（面积或体积）成比例，称这种概率模型为几何概率模型，简称为几何概型。

（2）几何概型中每个基本事件的发生都是等可能的，所有的基本事件有无限个。

设计意图：通过对三个不同情境中问题的探索、分析和总结，学生逐步建立了几何概型的概念，弄清了几何概型的基本特点和找到了计算方法，培养了学生的抽象概括能力和数学建模能力。

5.领悟新知，应用问题。通过相关练习或相关问题讨论，让学生进一步深入到知识的内部，领会知识的内涵，使知识与思维、情感、态度和价值观等一起成为学生生命的有机成分。

例1.将情境1中小圆区域等分为四部分，并移动位置成为图2所示图形，假设飞镖落点位于阴影区域时才能去看电影，则小张周末去看电影的概率是多少？

图2

学生活动：易判断该问题为几何概型，算得其概率为1/4，与情境1问题的概率相同。引导学生认识到，几何概型中事件A的概率只与区域的几何度量大小有关，与其位置和形状无关。

设计意图：通过实例练习，学生对几何度量的价值及其选择标准有更深刻的体会，提高了新知识在知识结构中的可利用性。

6.升华知识，拓展问题。将问题进行拓展，让学生在探究问题的过程中升华知识，产生无法预知的令人震撼动态生成的场面，使学生的主体地位得到尊重，自我价值得以实现。

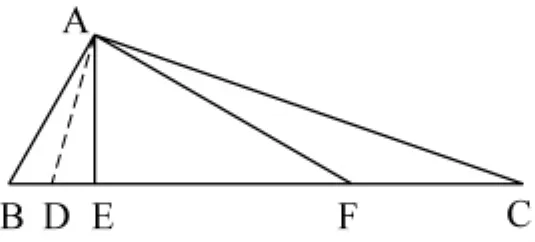
图3

例2.已知ΔABC中，∠ABC＝60°，AB＝2，BC＝6，在BC上任取一点D，则ΔABD为钝角三角形的概率是多少？

学生活动：如图3，当BE＝1时，∠AEB为直角，则D点在线段BE（不包含B、E点）上时，ΔABD为钝角三角形；当BF＝4时，∠BAF为直角，则D点在线段CF（不包含C、F点）上时，ΔABD为钝角三角形，所以ΔABD为钝角三角形的概率为

本问题基本事件发生的区域需要学生确定，这是建模的一个难点。在自主探究和小组讨论后，让学生总结出“先确定临界点，再确定区域”的方法。如果突破了这个难点，新知识就得到了升华。

三、问题引领式数学生态课堂的实施条件

1.对学生的要求。一是充分表达。在领受、领悟和提升的任何一个阶段中，学生都必须充分地表达自己的见解和看法，进行思想交流和交锋，这是合作研讨的前提。二是质疑争辩。在生态课堂中，学生可以随时提出自己的疑惑，也可以对同伴进行质疑，在讨论、争辩和释疑中厘清问题，消除困惑，这是有效建构的基础。三是纠改错。失败是成功之母，学习者总是在纠偏中前行，在改错中进步，生态课堂允许学生不断纠正偏差和尝试错误，这是知识升华的起点。

2.对教师的要求。一是变“教师”为“导师”。没有这个角色的转变，便不能为学生的学习与成长创设自由、和谐、快乐、尝试的生态课堂。二是从“前台”到“后台”。教师在后台为学生提供学习服务，建议学习形式，点拨学习困惑。三是变“讲授”为“引领”。在突破学习难点的关键时刻，教师建立起新颖独到的生态学习环境，引导学生排除学习障碍，收获成功喜悦，形成高峰体验。

参考文献：

［1］朱开炎.生本教育的生态课堂教学模式［J］.课程·教材·教法，2004（05）.

［2］窦福良.生态化课堂中的教师角色［J］.新课程研究·基础教育，2007（04）.

［3］詹明道.走向数学生态课堂［M］.南京：东南大学出版社，2008.

中图分类号：G633.6

文献标识码：A

文章编号：1673-9884（2016）02-0058-03

收稿日期：2015－12－19

基金项目：福建省教育科学“十二五”规划课题（2015XB0424）

作者简介：魏有莲（1967－），女，福建三明人，三明市第一中学高级教师。