基于地学工作流的交通预测过程模型设计与实现

李欣，黄鹏

(1.济南市勘察测绘研究院，山东 济南　250013；　2.山东省城市空间信息工程技术研究中心，山东 济南　250013；3.武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉　430079)



基于地学工作流的交通预测过程模型设计与实现

李欣1，2*，黄鹏3

(1.济南市勘察测绘研究院，山东 济南250013；2.山东省城市空间信息工程技术研究中心，山东 济南250013；3.武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉430079)

摘要：采用面向过程的建模思想，建立地学环境下交通预测的过程元模型，采用有向图方法对其过程逻辑进行描述，最后将过程模型向WF工作流框架进行映射。实验中，以交通预测的四阶段法作为过程建模的研究实例，对武汉1+8城市圈的交通量的分配进行了预测，验证了方法的可行性。

关键词：交通预测；过程元模型；有向图；WF工作流

1引言

在国民经济持续快速发展的时代背景下，交通规划在促进社会经济健康发展，保障城市各项功能正常运转等方面发挥了重要作用。交通预测是交通规划的重要组成部分，它为城市及区域交通规划提供了重要的数据基础[1]。随着GIS技术的发展，空间信息的可视化表达和分析功能在交通预测中的作用日益明显[2]，这也使得交通预测的处理过程更加复杂，而传统的过程描述方法已不能满足对空间处理的逻辑支持。为了更好地支持GIS环境中交通预测所表现出来的空间特性，本文引入地学工作流[3～5]对其处理过程进行描述，以进一步简化交通预测的操作流程，提升交通规划预测模型与空间模型集成应用的效率。

2理论与方法

2.1交通预测的过程元模型

构建交通预测的过程元模型，实际上是构建面向交通GIS过程建模的参考模型。交通预测的过程建模，不再是单一的业务过程建模，或者是空间过程建模[6]，而是一个混合结构的过程分析建模。本文所关注的重点，是建立起面向混合过程结构的过程元模型，来指导交通预测的过程建模。针对GIS支持下交通预测的过程特点，可以抽象出过程的三种基本要素：过程数据、过程活动和过程关系流，如图1所示。

(1)过程数据

过程数据可分为三种类型，其中一种是空间数据，一种是交通数据，还有一种是过程控制数据。空间数据主要涵盖了基本空间信息和属性信息，数据的载体多为shapefile，tiff等数据格式；而交通数据则以数据报表(如Excel表)为主要内容，实现对交通业务属性的描述；过程控制数据，主要用来控制处理过程中数据流的迁移，贯彻于整个处理过程的始末。

(2)过程活动

过程活动分为两种类型，一种是原子过程，另一种是过程链，又叫复合过程。

①原子过程

原子过程分为交通处理过程和空间处理过程。交通处理过程调用专业的数学模型来完成对业务数据的统计分析，根据交通处理模型的共同特点，抽象出以下几类基本要素，即名称，输入，输出，参数和方法。

空间处理过程通过调用空间算法来完成相应的空间分析功能，与交通处理过程的主要区别在于受到空间语义的约束，与时间和空间信息相关。定义空间处理过程的概念模型为GeoProcess，GeoProcess除了包含已有的输入、输出、参数和方法外，还包括对空间参考的定义。这主要是由于不同类型的空间数据集在处理过程中，必须考虑空间参考定义是否一致的问题，如空间分析中常用的数据裁剪操作。

②过程链

处理链元模型主要用来实现对复合过程的描述，其中也包含对过程关系流的定义。如所有的原子过程一样，过程链(ProcessChain)也具有inputs，outputs和parameters属性，其中inputs和outputs定义了它开始和结束的数据部分。而通过inputs，outputs或parameters属性暴露出来的数据对于外部处理的链接也都是可用的。

(3)过程关系流

过程关系流定义了各过程活动之间的逻辑关系，完成了各个过程活动之间的调用和衔接，并反映了整个处理过程中数据的流转状况，构成分析应用的控制流和数据流。

2.2交通预测的过程描述方法

虽然已经定义了面向交通预测的过程元模型，但仍然只是一个抽象的概念框架，还缺乏对处理过程有效的描述手段。换言之，过程元模型帮助我们了解了GIS环境下交通预测处理过程的主要特征和组成结构，但还需要一种更为具体的过程建模手段来承载过程逻辑的表达。

船型组合④：A、B泊位停靠1000DWT杂货船：10 + 85 + 50 +125 + 22.5 = 292.5m ＜ 300m

基于有向图的过程模型是一种图形化的过程建模手段[7]，在交通预测的建模环境下，本文对有向图过程模型进行了一定的扩展，引入了对空间数据和空间处理过程的信息描述。有向图的节点同样分为两种类型：数据节点，处理过程节点。其中，数据节点用来承载交通数据和空间数据的表达，作为处理过程节点的输入或输出。处理过程节点则用来反映交通分析预测的空间处理过程和业务处理过程，涵盖了“与”及“或”的逻辑处理关系。有向图的过程描述方法如图2所示。

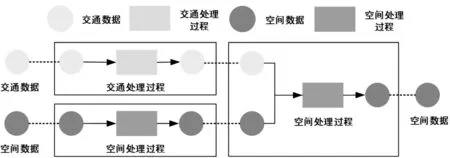
图2有向图过程描述方法

2.3交通预测的工作流映射

交通预测的过程建模，仅仅是对处理过程的抽象定义和描述，还不能被工作流引擎识别，必须将其映射到具体、可执行的工作流实例，才能为计算机所执行。

考虑到交通预测的过程建模特点，本文采用微软的WF工作流框架(Workflow Foundation)来实现对交通预测的工作流环境支持。WF提供了过程定义工具，过程描述语言及工作流引擎一整套机制[8，9]，但WF并不是一个完整的工作流产品，而是一个可扩展的工作流基础框架，用户需要根据自己的业务特点，对WF基础框架进行一定程度的扩展，这也使得交通预测过程模型向WF映射成为可能。这其中最关键的部分，就是实现数据节点和处理过程节点向WF活动模型(Activity Model)的映射。

(1)数据节点映射

在WF模型中，为了支持数据结点的路径获取功能，定义了基于CodeActivity的派生活动类型DataActivity，它只有一项基本属性即DataSource，用户通过对该属性的定义，就能实现输入、输出路径的描述。为了区分交通业务数据和空间数据，又可以派生出两种新的类型，即TrafficDataActivity和GeoDataActivity，如图3所示，这两种类型没有本质上的不同，只是在获取路径的方式上有所区别，比如，前者需要获取的是Excel表的文件路径，而后者还需要支持空间数据库环境下的路径信息获取。

(2)处理过程节点映射

①原子处理过程节点映射

根据定义了的交通处理过程的概念模型，即TrafficProcess，其中包括Inputs，Outputs，Parameters和Method的定义，而在WF模型中，CodeActivity本身包含了InArguments、OutArguments以及Execute方法的定义，因此我们可以定义TrafficProcessActivity来支持TrafficProcess的概念模型。其具体映射关系如图4所示。

图4交通处理过程节点映射

②空间处理过程调用的处理模型与交通处理过程有着本质上的不同，因此定义了GeoProcessActivity来支持对概念模型的映射。同时，空间处理过程还包含了对空间参考的定义SpatialReference，这是因为空间数据本身受到空间语义的约束，需要定义空间处理的空间参照系对其进行条件约束，其映射关系如图5所示。

图5空间处理过程节点映射

③复合过程链映射

复合过程链(ProcessChain)本身也包含对Inputs、Outputs、Parameters的定义，与普通处理不同的是，它由多项处理过程共同构成，因此还包含对Processes和Connections(连接弧)的定义。而在WF环境下，对复合过程链最好的支持对象便是Flowchart。Flowchart是为NativeActivity类型的内置活动，它通过Nodes属性记录了活动列表，如图6所示，同时在内部支持活动的管理和调用，并可以再次封装为一项独立处理过程，嵌入更高层次的活动中去执行。

图6复合过程链映射

3实验

3.1实验背景与数据

交通量预测是交通需求预测的核心内容，其涉及的模型算法复杂，空间分析模型与交通规划模型间的集成应用也较多，因此，实验将从交通量预测的四阶段法[10]入手，选取“武汉1+8城市圈”作为本次实验的研究区域，重点研究交通预测处理过程在WF工作流环境下的实现方法，并执行最终生成的过程实例。

实验采用的数据分为空间数据和交通业务数据两大类别，其中，空间数据用来支持交通需求量的图形表达和空间分析，主要包括武汉城市圈行政区划图和路网数据集；交通业务数据用来满足交通预测数学模型的数据需求，主要包括武汉城市圈2006年客车OD表，如表1所示。

3.2实验结果与分析

(1)实验过程与结果

四阶段法将交通预测划分成4个阶段，即交通生成预测，交通分布预测，交通方式划分，交通分配，空间处理对交通生成预测、分布预测的结果进行图形展示，并采用最短路径法对交通量的预测结果进行分配处理。

交通生成预测是指预测各小区的交通发生总量和交通吸引总量，构建的交通生成预测的过程实例如图7所示。在交通生成预测过程实例的基础上，WF工作流引擎将根据既定的处理流程执行每一项处理操作，并在指定的路径下生成最终结果。图8展示的是各小区交通生成量的专题地图。

交通分布与方式划分是交通预测的两个阶段，其最终目的是获得各交通小区间分运输方式的OD矩阵。

交通分配是交通需求预测中最复杂的处理阶段，其主要目的是将预测得到的交通量分配到实际的路网中去。图9则反映了交通分配阶段完整的处理过程实例，得到了反映各区域路段交通量的专题地图如图10所示。

(2)实验分析

从实验的最终结果来看，本文提出的交通预测过程建模方法，较好地实现了地学处理环境下空间分析模型与交通业务模型的集成应用，简化了交通预测的处理流程。其主要优点是实现工作流环境下的交通预测过程的快速建模，同时支持对空间处理的过程描述，从而更好地实现GIS与交通预测专业技术的集成应用。

4结语

为了有效地简化交通预测的建模过程，本文引入了工作流技术，考虑空间信息领域和交通规划领域的特点，提出了面向交通预测的过程模型框架，并向WF工作流模型进行了映射处理，得到了可被工作流引擎支持的过程模型实例。通过实验，在WF环境下，运行建模得到的过程实例，生成了反映武汉城市圈中各城市间交通分布情况的专题地图，验证了方法的可行性。同时，地学处理工作流的人机交互问题和过程模型间组合的有效性验证问题仍有待作进一步的研究。

参考文献

[1]陆化普. 交通规划理论与方法[M]. 北京：清华大学出版社，1998：51～52.

[2]刘学军，徐鹏. 交通地理信息系统[M]. 北京：科学出版社，2006：87～89.

[3]柳琳. 基于工作流的地理处理建模技术[J]. 地理空间信息，2011，09(1)：39～42.

[4]王艳军，邵振峰，慎于蓝. 基于工作流引擎的空间信息服务链半透明构建技术研究[J]. 测绘通报，2012(3)：26～28.

[5]于海龙，邬伦，刘瑜等. 基于Web Services的GIS与应用模型集成研究[J]. 测绘学报，2006，35(2)：153～159.

[6]高勇，邬伦，刘瑜等. 空间信息处理过程建模研究[J]. 北京大学学报(自然科学版)，2004，40(6)：914～921.

[7]陈张，赵卫东. 基于有向图的工作流模型的研究[J]. 计算机技术与发展，2006，16(4)：69～72.

[8]苗林，金涛，王建民等. XPDL模型到WWF模型转换技术的研究[J]. 计算机研究与发展，2009，46(z2)：540～546.

[9]杨利国. 基于WF工作流技术研究及应用[D]. 武汉理工大学，2008.

[10]邵春福. 交通规划[M]. 北京：邵春福，2012：132～135.

Design and Implementation of the Process Model of Traffic Forecasting

Li Xin1，2，Huang Peng3

(1.Jinan Geotechnical Investigation and Surveying Institute，Jinan 250012，China；2.Shangdong Engineering Technology Research Center of Urban Spatial Information，Jinan 250013，China；3.State Key Laboratory for Information Engineering in Surveying，Mapping and Remote Sensing，Wuhan University，Wuhan 430079，China)

Key words：traffic forecasting；process meta-model；directed graph；workflow of WF

Abstract：We propose a process meta-model of traffic forecasting based on the thought of process oriented，then describe the process by the directed graph，make the process model mapped to the workflow of WF. The experiment uses the traffic data of Wuhan City Cycle，the result demonstrates the usefulness and feasibility of the method.

文章编号：1672-8262(2016)03-25-05

中图分类号：P208.2

文献标识码：A

*收稿日期：2016—01—19

作者简介：李欣(1984—)，男，硕士，助理工程师，主要从事地理信息系统研发工作。

基金项目：国家863计划课题(2013AA010308)