The Twin Domination Number of Lexicographic Product of Digraphs

MA Hong-xia, LIU Juan

(College of Mathematical Sciences, Xinjiang Normal University, Urumqi 830054, China)



The Twin Domination Number of Lexicographic Product of Digraphs

MA Hong-xia, LIU Juan*

(College of Mathematical Sciences, Xinjiang Normal University, Urumqi 830054, China)

Letγ*(D) denote the twin domination number of digraphDand letDm[Dn] denote the lexicographic product ofDmandDn, digraphs of orderm,n≥2. In this paper, we first give the upper and lower bound of the twin domination number ofDm[Dn], and then determine the exact values of the twin domination number of digraphs:Dm[Kn];Km[Dn];Km1,m2,…,mt[Dn];Cm[Dn];Pm[Cn] andPm[Pn].

twin domination number; lexicographic product; digraphs

LetDm=(V(Dm)，A(Dm))andDn=(V(Dn)，A(Dn))betwodigraphswhichhavedisjointvertexsetsV(Dm)={x0，x1，…，xm-1}andV(Dn)={y0，y1，…，yn-1}anddisjointarcsetsA(Dm)andA(Dn),respectively.ThelexicographicproductDm[Dn]ofDmandDnhasvertexsetV(Dm)×V(Dn)={(xi,yj)|xi∈V(Dm),yj∈ Vn}and(xi,yj)(xi′,yj′)∈A(Dm[Dn])ifoneofthefollowingholds:(a) xixi′∈A(Dm);(b) xi=xi′andyjyj′∈A(Dn).

Inrecentyears,thedominationnumberofsomedigraphshasbeeninvestigatedin[7～16].However,todatefewresearchabouttwindominationnumberhasbeendoneforlexicographicproductofdigraphs.Inthispaper,westudythetwindominationnumberofDm[Dn].Firstly,wegivetheupperandlowerboundofthetwindominationnumberofDm[Dn],andthendeterminetheexactvaluesofthetwindominationnumberofdigraphs: Dm[Kn];Km[Dn];Km1,m2;…;mt[Dn]; Cm[Dn]; Pm[Cn]andPm[Pn].

1 Main results

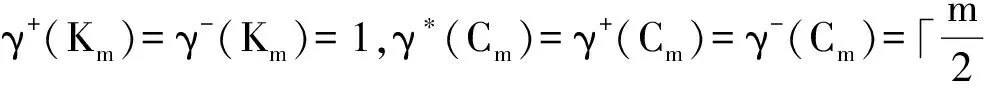
Lemma 1 For anym,n≥2, thenγ*(Dm)≤γ*(Dm[Dn])≤γ*(Dm)γ*(Dn).

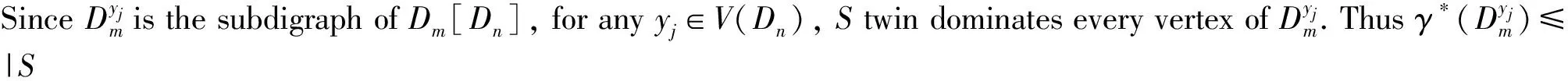
Now we prove thatγ*(Dm)γ*(Dn)≥γ*(Dm[Dn]). LetS1={xi1,…,xit} be a minimum twin dominating set ofDm. LetS2={yj1,…,yjw} be a minimum twin dominating set ofDn. SetS′={(xik,yjl)|xik∈S1,yjl∈S2}. For any vertex (xi,yj)∈V(Dm[Dn]), ifxi∈S1andyj∈S2, then (xi,yj)∈S′. Ifxi∈S1andyj∉S2, there must existyjl,yjl′∈S2, such thatyjlyj,yjyjl′∈A(Dn). Since (xi,yjl)(xi,yj),(xi,yj)(xi,yjl′)∈A(Dm[Dn]) and (xi,yjl),(xi,yjl′)∈S′, (xi,yj) is twin dominated byS′. Ifxi∉S1, there must existxik,xik′∈S1such thatxikxi,xixik′∈A(Dm), and there must existyr∈S2such that (xik,yr)(xi,yj),(xi,yj)(xik′,yr)∈A(Dm[Dn]) and (xik,yr), (xik′,yr)∈S′, so (xi,yj) is twin dominated byS′.

Therefore,S′ is a twin dominating set ofDm[Dn] and |S′|=|S1||S2|=γ*(Dm)γ*(Dn). Thus,γ*(Dm[Dn]) ≤γ*(Dm)γ*(Dn).

Clearly, the following theorem is obtained from Lemma 1.

Theorem 1 For anym,n≥2, thenγ*(Dm[Dn])=γ*(Dm) if and only ifγ*(Dn)=1.

According to Theorem 1, the following theorem is obvious.

Theorem 2 For anym,n≥2, thenγ*(Dm[Kn])=γ*(Dm).

Theorem 3 For any complete digraphKmand digraphDn, then

Proof By Lemma 1 and Theorem 1, it is clear thatγ*(Km[Dn])=1 ifγ*(Dn)=1. It is easy to see thatS={(x0,y0)} is a twin dominating set ofKm[Dn], where {y0} is a twin dominating set ofDn.

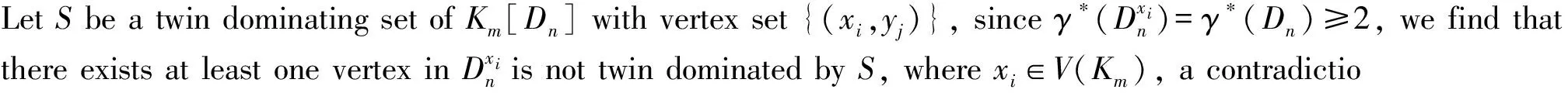
LetKm1,m2,…,mtbe the completet-partite digraphs. The next Theorem is obtained by Lemma 1 and Theorem 3.

Theorem 4 Letmi≥1, for anyi∈{1,2,…,t}. Then

WeemphasizethatverticesofadirectedcycleCnarealwaysdenotedbytheintegers{0,1,…,n-1},consideringmodulon,throughoutthispaper.ThereisanarcxyfromxtoyinCnifandonlyify≡x+1(modn).Forthefollowingaddition,wealwaysconsidermodulon.

Theorem 5 Form,n≥2, we have

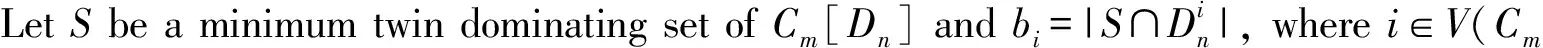
Nowweconsidertwocases.

Case1γ+(Dn)=γ-(Dn)=1andγ*(Dn)≥2.

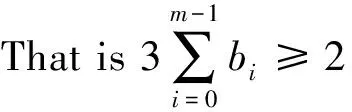
Let{yj1}and{yj2}beout-dominatingsetandin-dominatingsetofDn,respectively.Set

S3={(m-1,yj2)}.

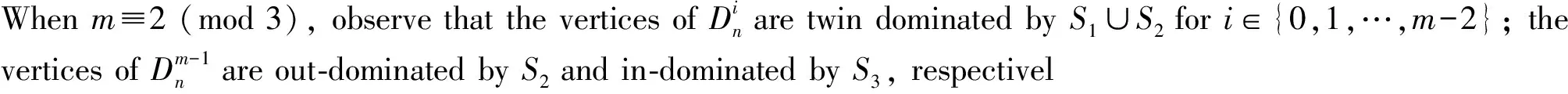
Case2γ*(Dn)≥2andγ+(Dn)≥2orγ-(Dn)≥2.

Withoutlossofgenerality,weassumethatγ+(Dn)≥2.Itfollowsthatγ-(Dn)≥1,thatisγ+(Dn)≥γ-(Dn).Inthiscase,letJ={i|i∈{0,1,…,m-1}}suchthatbi=0andletJ′={i|i-1∈J}.ItiseasytoseethatJ∩J′=∅.

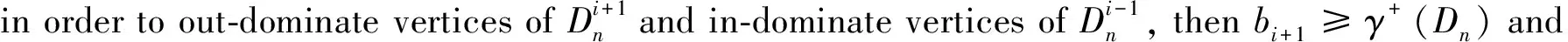
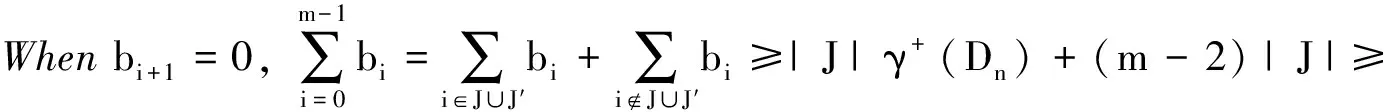
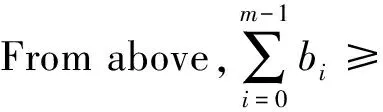
Forcovenience,letPmbeadirectedpathwithvertexset{0,1,…,m-1}inthesequel.

Theorem6Letm,n≥2,then

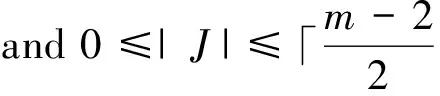
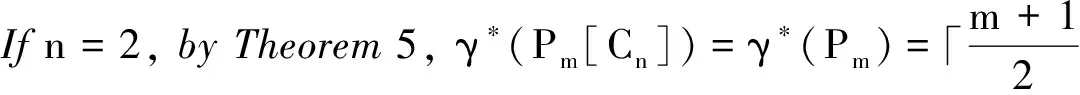
Next,weconsidern≥3.Forconvenience,wefirstcountthenumberofbifromi=1toi=m-2.Therearetwocasestobeconsidered:

Case1bm-2≠0.

Then

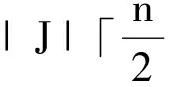
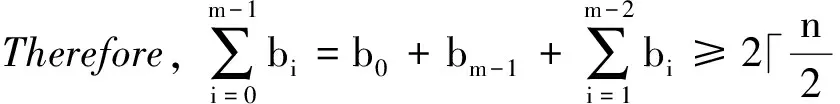
Case2bm-2=0 (thatis|J|≥1).Weconsiderthefollowingtwosubcases:

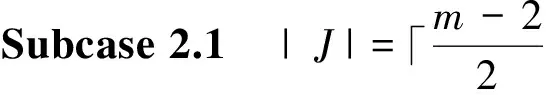
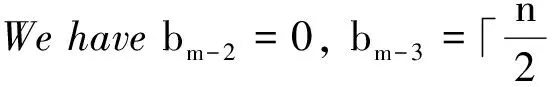
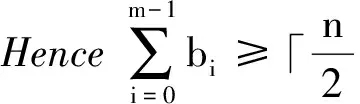
Itfollowsthattheremustexistsomeevenintegerjsuchthatbm-j≠0.Then

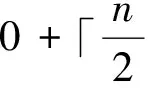
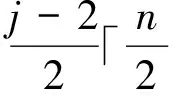
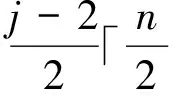
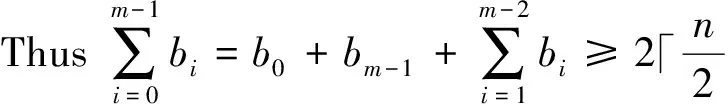
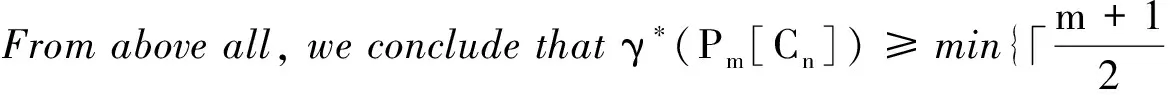
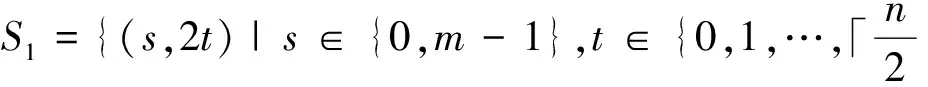
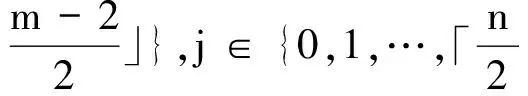
S3={(i,0)|i∈{1,2，…，m-2}}.

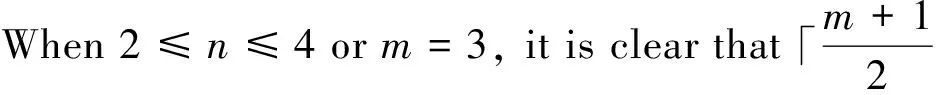
ThefollowingCorollaryisobtainedfromTheorem6.

Corollary1Letm,n≥2,then

ProofTheframeworkandmainideaforthisproofarethesameasthatofTheorem6.Thepointtobemodehereisthatforthecasem≠3,oneshouldconsiderfoursubcases.n=2,3,4andn≥5.Hence,theproofisleftforthereaders.

[1] ARAKI T. Thek-tuple twin domination in de Bruijin and Kautz digraphs [J]. Disc Math, 2008,308(24):6406-6413.

[2] ARAKI T. Connectedk-tuple twin domination in de Bruijin and Kautz digraphs [J].Disc Math, 2009,309(21):6229-6234.

[3] ARUMUGAM S, EBADI K, SATHIKALA L. Twin domination and twin irredundance in digraphs [J]. Appl Anal Disc Math, 2013,7:275-284.

[4] CHARTRAND G, DANKELMANN P, SCHULTZ M,etal. Twin domination in digraphs [J].Ars Comb, 2003,67:105-114.

[5] SHAN E F, DONG Y.X, CHENG Y K. The twin domination number in generalized de Bruijn digraphs [J]. Inform Process Lett, 2009,109(15):856-860.

[6] WANG Y L. Efficient twin domination in generalized De Bruijn digraphs [J]. Disc Math, 2015,338(3):36-40.

[7] CAI H, LIU J, QIAN L. The domination number of strong product of directed cycles[J]. Disc Math Algor Appl, 2014,6(2):1-10.

[8] LIU J, ZHANG X D, CHEN X,etal. The domination number of Cartesian products of directed cycles [J]. Inform Process Lett, 2010,110(5):171-173.

[9] LIU J, ZHANG X D, MENG J. On domination number of Cartesian product of directed path [J]. J Comb Optim, 2011,22(4):651-662.

[10] MOLLARD M. On the domination of Cartesian product of directed cycles: Results for certain equivalence classes of lengths [J]. Discuss Math Graph Theory, 2013,33(2):387-394.

[11] MOLLARD M. The domination number of Cartesian product of two directed paths [J].J Comb Optim, 2014,27:144-151.

[12] SUMENJAK T K, PAVLIC P, TEPEH A. On the Roman domination in the lexicographic product of graphs [J]. Disc Appl Math, 2012,160(13-14):2030-2036.

[13] SUMENJAK T K, RALL D F, TEPEH A. Rainbow domination in the lexicographic product of graphs [J]. Disc Appl Math, 2013,161(13-14):2133-2141.

[14] YUE W, HUANG Y, ZHAO T,etal. The crossing number of join products of a special 5-vertex graph withCn[J]. J Natur Sci Hunan Norm Univ, 2015,38(1):81-85.

[15] SHAHEEN R S. Domination number of toroidal grid digraphs [J]. Utilitas Math, 2009,78:175-184.

[16] ZHANG X D, LIU J, CHEN X,etal. On domination number of Cartesian product of directed cycles [J]. Inform Process Lett, 2010,111(1):36-39.

(编辑 HWJ)

2016-05-03

国家自然科学基金资助项目(11301450,61363020，11226294)；新疆自治区青年科技创新人才培养工程资助项目(2014731003)

有向图字典式积的双控制数

马红霞，刘 娟*

(新疆师范大学数学科学学院，中国 乌鲁木齐 830054)

令γ*(D)表示有向图D的双控制数，Dm[Dn]表示有向图Dm和Dn的字典式积，其中Dm,Dn的阶数m,n分别大于等于2.本文首先给出Dm[Dn]的双控制数的上下界，然后确定如下有向图的双控制数的确切值：Dm[Kn];Km[Dn];Km1,m2,…,mt[Dn];Cm[Dn];Pm[Cn]及Pm[Pn].

双控制数；字典式积；有向图

10.7612/j.issn.1000-2537.2016.06.014

*通讯作者,E-mail：liujuan1999@126.com