阅读或引用文献时要有质疑精神

北京丰台二中　　甘志国　　(邮编：100071)



数学

阅读或引用文献时要有质疑精神

北京丰台二中甘志国(邮编：100071)

摘要我们在阅读或引用文献时要有质疑精神：首先，我们要弄懂阅读或引用的文献，尽可能的推算，判断它们的正确性，自己没弄明白的文献(哪怕是权威的文献)引用时要谨慎；其次，若阅读或引用的文献又是从别处引用的，要尽可能的查到原文献，防止引用的过程中出现错误；最后，要有质疑的精神，对阅读或引用的文献，要研究它们是否正确，能否简化和推广等等.

关键词阅读文献；引用文献；质疑精神；整数性质

1“三十年备一课”中的错误——当正整数n=____时，4729494n+1可以是完全平方数

文献第23页的第4.1节“三十年备一课”中引用了文献中的一个例子：

当n∈R*时，f(n)=4729494n+1的值能是完全平方数吗？

依次令n=1,2,3,…,505494852343150330

74477819735540408986339时，f(n)的值均不是完全平方数.

由此似乎可以下结论：当n∈R*时，f(n)=4729494n+1的值均不是完全平方数.

但是，当n的值再增加1即当n=50549485234315033074477819735540408986340时，f(n)=1099319867328297349798662328214

33543901088049却是一个45位数的完全平方数.

文献还说：

引用该例的目的是通过“大数字”的视角冲击，从数学知识的角度再次强调用数学归纳法解题时，两个步骤缺一不可.同时该例也很有趣，可以活跃课堂气氛.

可以说最近一次上这节课(2015年6月在上海市光明中学为在该校研修的天津市部分骨干教师上的展示课)积累了笔者30年的经验，虽然不敢说这样就能上好，但至少态度是认真的.

说30年备一节课似乎有点夸张，其实是在30年前的基础上，每次上这一课都把自己最近的想法再结合学生的情况在前一次教学的基础上修修改改.

笔者发现，文献,中叙述的结论是错误的：由恒等式(x-1)(x+1)+1=x2可知：

当n=4729492时，f(n)=4729494×4729492+1=47294932是完全平方数；

当n=4729496时，f(n)=4729494×4729496+1=47294952也是完全平方数.

全国初等数学研究会第三届理事会第五次常务理事扩大会议于2015年7月15、16日在北京召开，笔者与文献的作者文卫星老师都参加了这次会议.

笔者多次拜读过文老师在刊物上发表的文章，受益匪浅.在会议之余，笔者与文老师聊了很多，了解到文老师早年从江苏省来到上海市的重点中学(七宝中学)任教，由于工作认真、业绩突出，较快地评上了特级教师.

虽然文老师“三十年备一课”，但仍然出现了瑕疵(“玉有瑕疵也斑斓”)，这说明老师在备课时要“认真认真再认真”，引用文献中的结论时对该结论要尽可能的给予验证(要有质疑的态度，不可以讹传讹)；学生在听课时也要有质疑的态度.

2240≈1.2×1012吗？

中国初等数学权威期刊《数学通报》(中国数学会与北京师范大学主办)2002年第1期发表了文章《引无数英雄竟折腰的3x+1猜想》[3],该文第五段是：

“这是偶然的巧合吗？无论用手工计算还是计算机检验，人们都发现上述结论是对的.如日本东京大学米田信夫验算x=240(大约是12000亿)以下所有的自然数，答案都是1.自然数有无限多个，对一切自然数‘3x+1’问题都成立吗？”

文献末也写到：

“到目前为止，数学家已借助电子计算机验证了240≈1.2×1012以内的自然数对叙拉古猜想(即3x+1问题)均成立.究竟何时才能完全解决这个问题？也许要留待二十一世纪的数学家来作出回答.”

笔者发现，早年叙述著名的3x+1问题(也叫3x+1猜想、叙拉古猜想、科拉兹猜想、角谷猜想、哈塞猜想)时都有“240≈1.2×1012(也即约为12000亿)”的叙述，实际上，这是不对的，误差太大：使用一下电脑上的计算器(科学型)或者笔算，均可得240=1099511627776(≈1.1×1012)，所以，以上错误应尽早更正.

近日笔者读到专著第11页第二段末的叙述：

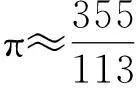
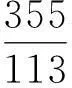
(2)按精确值“π=3.14159265358979…”(见文献第121页或网络http://baike.baidu.com/view/38305.htm)来计算直径为十公里(即107毫米)的圆的周长是

3.14159265358979…×107=31415926.5358979…(毫米).

因为31415929.2035398…-31415926.5358979…=2.667641…<3.

所以专著中的上述叙述是错误的，应修正为：

普通高中课程标准实验教科书《数学·选修3-1(数学史选讲)·A版》(人民教育出版社2007年第2版)第34页第一行也是这样写的.

还有许多人计算过更精确的圆周率.比如十六世纪德国有个叫卢道尔夫的人，他几乎花费了毕生的精力，把圆周率算到了小数点后面35位.他嘱咐他的孩子，在他死后，要把他计算的圆周率刻在他的墓碑上.他计算的圆周率为：

3.14159265358979323846264338327950288

现在用电子计算机，可以把圆周率的数值算到几十万位.其实，把圆周率的数值没完没了地算下去，并没有什么使用价值.我们要计算地球赤道的周长，要求误差不超过一厘米，只要把圆周率取到小数点后面第九位就够了.

因为通常认为地球的半径是6371km=6.371×108cm，所以地球赤道的周长是

2π×6.371×108cm.

若把圆周率取到小数点后面第九位(应按四舍五入法来取)，算得地球赤道的周长是

2×3.141592654×6.371×108cm.

所以误差是

2(3.141592654-π)×6.371×108=2×0.0410206…×6.371=0.52268…<1(cm).

4数学家很可能没有提出过这些猜想

文献[10]写道：

我们知道，当m≥2时，欧拉函数φ(m)=p1α1-1…pkαk-1(p1-1)…(pk-1),其中

m=p1α1…pkαk(pi是互不相同的素数，αi∈R*,i=1,…,k)

①

关于φ(m),有一个迄今未得证实的猜想，不存在满足φ(m)=m-1的合数m，这是半世纪前莱梅(Lehmer)提出的.

下面的定理1说明了这个猜想成立.

定理1当m≥2时，φ(m)≤m-1(当且仅当m是素数时取等号).

证明当a1,…,ak∈R+,k≥2时，有a1…ak<(a1+1)…(ak+1)-1.

当a1,…,ak∈R+时，有a1…ak≤(a1+1)…(ak+1)-1 (当且仅当k=1时取等号).

由此，得

(p1α1-1)…(pkαk-1)≤p1α1…pkαk-1(pi是互不相同的素数，αi∈R*,i=1,…,k)(当且仅当k=1时取等号)

②

设m为①的形式，得

piαi-1(pi-1)=piαi-piαi-1≤piαi-1(当且仅当αi=1时取等号)(i=1,…,k)，

所以(p1α1-1)…(pkαk-1)(p1-1)…(pk-1)≤(p1α1-1)…(pkαk-1)(当且仅当α1=…αk=1时取等号).

又由②，得

(p1α1-1)…(pkαk-1)(p1-1)…(pk-1)≤p1α1…pkαk-1(当且仅当k=1,α1=1时取等号).

即定理1成立.

笔者认为，数学家莱梅(Lehmer)很可能没有提出文献[10]中叙述的这个猜想：这位数学家应当很容易解决此猜想.

文献[11]写道：

著名数学家Goldbachc曾提出：“(3m+2)n2+3对于任何整数m和n的人数都不可能排成方队.”Euler证明了这个结论，并提出4mn-m-n人也不能排成方队.但要证明Euler的结论就难了.

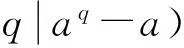
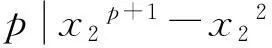
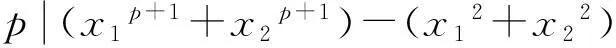
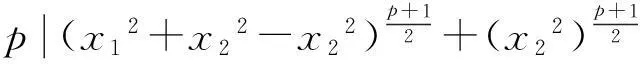
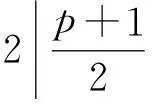
下面用定理2来证明上段话中的两个猜想均正确：

(1)方程(3m+2)n2+3=t2没有整数解.

证明假设该方程有整数解(m,n,t),可得

(2)方程4mn-m-n=t2没有正整数解.

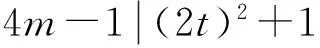
这不可能，所以假设错误，即结论成立.

笔者认为，大数学家Goldbachc和Euler对于如此简单的猜想不可能不会证明.

5阅读或引用文献时要有质疑精神

我们在阅读或引用文献时要有质疑精神.

首先，我们要弄懂阅读或引用的文献，尽可能地推算，判断它们的正确性，自己没弄明白的文献(哪怕是权威的文献)引用时要谨慎；其次，若阅读或引用的文献又是从别处引用的，要尽可能的查到原文献，防止引用的过程中出现错误；最后，要有质疑的精神，对阅读或引用的文献，要研究它们是否正确，能否简化和推广等.

在这方面，中国古代杰出的布衣数学大师刘徽(约225～约295)堪称典范[12].

刘徽的治学思想，也倍受世人推崇.首先，他有孜孜不倦的学习态度，从《九章算术注》的序中所言“徽幼习九章，长再祥览”可见一斑.其次，他钻研学术严谨、求实，讲究“析理以辞，解体用图”，“约而能周，通而不黩”.对别人的错误绝不姑息，自己不懂也实言相告.刘徽发现了《九章算术》中球的体积公式有错误，但是经过长期的努力，也没用得出正确结果，这时他不是用一个改进的公式去代替，而是实事求是地说真话：“敢不阙疑，以俟能言者.”另外，在数学教学方面，他善于启发，主张“告往而知来，举一隅而三隅反”；还告诫后学者要抓住关键、提纲挈领.

参考文献

1文卫星.浅谈数学概念课教学.中学数学教学参考(上旬)，2016(1～2)：20-24

2洪波.怎样应用数学归纳法.上海：上海教育出版社，1979

3徐品方.引无数英雄竟折腰的3x+1猜想.数学通报，2002(1)：42-43

4洪伯阳.数论著名问题选介.华中师范大学学报(数学史专辑)，1987(3)：60-71

5天津人民广播电台科技组编.科学创造的艺术.北京：中国广播电视出版社，1987

6洪伯阳.关于π与e.华中师范大学学报(数学史专辑)，1987(3)：113-122

7甘志国著.初等数学研究(II)下.哈尔滨：哈尔滨工业大学出版社，2009.415

8甘志国.祖冲之的精细严密.少年智力开发报(数学专页·理科版)，2005年5月22日(第43期)

9谷超豪主编.数学词典.上海：上海辞书出版社，1992.669

10熊全淹.初等整数论.2版.武汉：湖北教育出版社，1989.63-64

11傅钟鹏.数学的魅力.福州：福建科学技术出版社，1985.109

12甘志国.高考压轴题(下).哈尔滨：哈尔滨工业大学出版社，2014.200

(收稿日期：2016-04-21)

园地