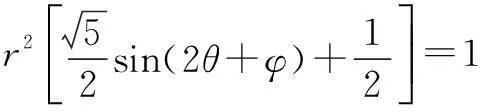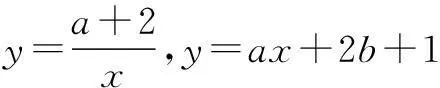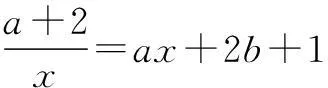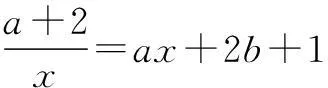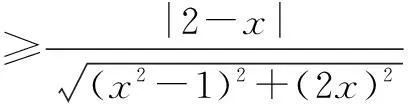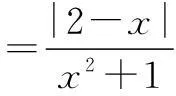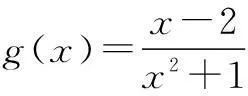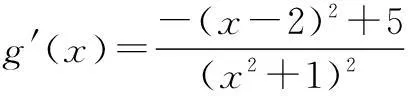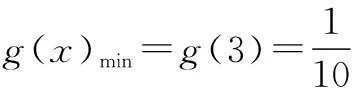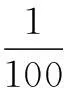用三角换元法解一类题

张　进

(江苏省南京市宁海中学，210024)



○学习指导○

用三角换元法解一类题

张进

(江苏省南京市宁海中学，210024)

换元思想是一种重要的数学思想方法.换元法又称辅助元素法、变量代换法,它通过引进新的变量把分散的条件联系起来，隐含的条件显露出来或者把条件与结论联系起来，将陌生的结构变为熟悉的形式,把复杂的计算和推证简化，换元的实质是转化.

本文主要针对笔者在最近高三复习课中遇到的一类具x2+y2的结构问题,利用三角换元法将问题化归到我们熟悉的模型中来,转变一种解决问题的思路,与广大读者交流,欢迎给予指导.

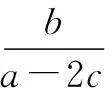
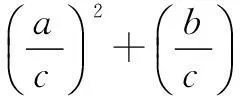
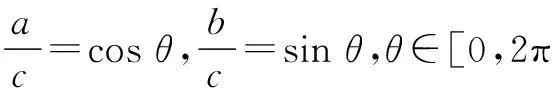
评注本题利用了三角换元法,将题中的三个参量减少为一个参量,并将问题转化为求直线与圆相交斜率的取值范围问题.通过这种换元,往往可以暴露已知与未知之间被表面形式覆盖着的实质,发现解题途径.与此类似的有:

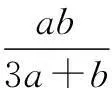
例2(2015年浙江高考题)已知实数x,y满足x2+y2≤1,则|2x+y-4|+|6-x-3y|的最大值是______.

分析从题目结构上看,可以考虑去绝对值从而转化为线性规划问题,笔者在此尝试三角换元法,做起来更为简单.

解设x=rcosθ,y=rsinθ,0

|2x+y-4|+|6-x-3y|=|2rcosθ

+rsinθ-4|+|6-rcosθ-3rsinθ|.

由三角函数和r的范围易将绝对值去掉,再由“辅角公式”可将原式化为:10-3rcosθ-4rsinθ=10-5rsin(θ+φ),易知其最大值为15.

评注此题本意考察简单线性规划内容,考试中避免不了要画图和利用点到直线距离公式的计算,笔者根据题中x2+y2≤1,考虑圆的参数方程,即三角换元法将其转化为三角函数的最值问题,简化了运算,在考试中也可节约时间.

例3设实数x,y满足x2+2xy-1=0,则x2+y2的最小值为______.

分析此题为二元二次函数的最值问题,常规解法是利用条件转化为一元函数最值问题.不过,笔者尝试对结论中的二元平方关系进行三角换元,亦可解决此题.

解设x2+y2=r2,x=rcosθ,y=rsinθ,r>0,θ∈[0,2π).将x,y代入原式得

r2cos2θ+2r2sinθcosθ-1=0,

从而r2(cos2θ+2sinθcosθ)=1,

变式设实数x,y满足x2+2xy-y2=1,则x2+y2的最小值为______.

此题笔者试着构造齐次式或者构造不等式求解,但都需要较强的基本功,对思维要求和运算能力的要求都很高,而用三角换元法则简化了运算,如下:

解设x2+y2=r2,x=rcosθ,y=rsinθ,r>0,θ∈[0,2π).将x,y代入原式得

r2cos2θ+2r2sinθcosθ-r2sin2θ=1,

分析本题的两条曲线的公共点,可转化为方程

即ax2+(2b+1)x-a-2=0.

在区间[3,4]上至少有一个解的问题.可以利用主次元转化的方法,视上述方程为关于a,b的直线方程(x2-1)a+2xb+x-2=0,再利用(a,b)到原点的距离大于等于原点到直线的距离求解，这种解法对学生的思维要求很高.

解设a2+b2=r2,a=rcosθ,b=rsinθ,r>0,θ∈[0,2π).

ax2+(2b+1)x-a-2=0,

所以x2rcosθ+2xrsinθ+x-rcosθ-2=0,

(rx2-r)cosθ+2xrsinθ=2-x,

因为|sin(θ+φ)|≤1,

在[3,4]上g′(x)>0,所以g(x)在[3,4]上是增函数，

评注用三角换元法解决此题思维较为自然,根据辅角公式以及三角函数的有界性来求解,将原先的几何问题转化为三角函数问题,此题再一次体现三角换元法的强大实用性.