双曲线渐近线方程统一形式的妙用
2016-07-07朱彤
高中数学教与学 2016年11期
朱 彤
(浙江省温州市教师教育院, 325002)
○短文集锦○
双曲线渐近线方程统一形式的妙用
朱彤
(浙江省温州市教师教育院, 325002)

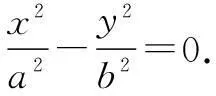

解由题意,点B,C的坐标是方程组
的解.
消去y,整理得
1.1 对象 选择2011年8月—2012年7月我院4个病区(呼吸内科、老年科、神经内科和骨科)护士54名,平均年龄(29.6 ±6.5)岁;平均工作时间(8.7 ±7.3)年;学历:硕士1名,本科15名,大专32名,中专6名;职务:护士长4名,护士50名;职称:护士26名,护师22名,主管护师6名。住院患者258例,男154例,女104例,平均年龄(65.7±17.5)岁,沟通良好,并取得患者本人同意。
bx=±(x+1),

∵|AB|=|BC|,
∴2xB=xA+xC,
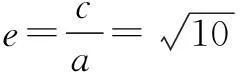


证明当直线l的斜率不存在时,由双曲线的对称性,结论显然成立.
当直线l的斜率为k,纵截距为m时,设点A,B,C,D的坐标分别为(xA,yA),(xB,yB),(xC,yC),(xD,yD).

b2x2-a2(kx+m)2-a2b2=0,
即(b2-a2k2)x2-2a2kmx-a2m2-a2b2=0,

(b2-a2k2)x2-2a2kmx-a2m2=0,
所以线段AB与CD的中点横坐标相等,由于A,B,C,D在同一直线上,故线段AB与CD的中点重合,故AC=BD.
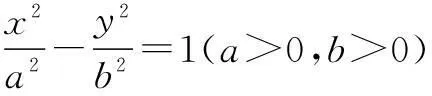
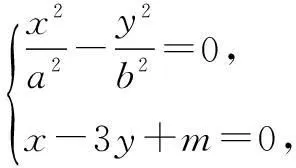
(9b2-a2)y2-6b2my+b2m2=0,

xA+xB=3(yA+yB)-2m

设AB的中点为Q,则

由|PA|=|PB|,得
PQ⊥AB,
化简得a2=4b2,

的解,消去y,并整理得



故a2b2x2-2a2b2x1x+a4b2=0,
即x2-2x1x+a2=0.

