不妨做个“坏”老师
2016-07-07吴新超
吴新超
不妨做个“坏”老师
吴新超

教学有法,但无定法。面对习以为常的教法,我们不妨换一种方法试试;面对循规蹈矩的设计,我们不妨换一个角度想想。这样一来,课堂会带给我们另一番风景。
一、“有意陷害”
案例:“复式条形统计图”教学片段
在初步认识了复式条形统计图后,教师用课件出示本班6个小组男女生1分钟跳绳平均数的统计图,一类直条是红色,另一类直条是蓝色,但是没有区分男女生的图例。
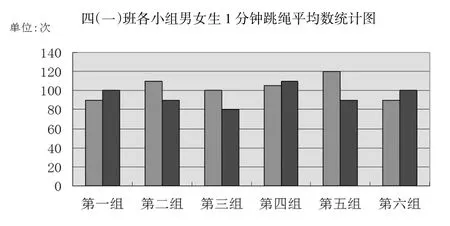
教师提问:“第一小组男生1分钟跳绳的平均数是多少?”
“90。”一个学生很快站起来回答道。(很显然,他把第一根红色的直条默认成男生的图例了)教师对这个回答既没有肯定也没有否定,只是拿着话筒在教室的小组间走来走去,不时将话筒送到学生面前。学生们一个个目瞪口呆、不知所措,教室里沉默了将近半分钟。
“老师,这个统计图没有图例,不知道哪类直条是男生的。”终于有一个学生打破了沉静。
“那刚才为什么有学生把红色的直条说成是男生的呢?”教师反问道。
“因为男生在统计图标题的前面。”
“因为红色的直条比蓝色的直条短一些,而男生一般比女生跳得少一些。”
“我们做统计图可不能凭主观印象乱猜测,应该实事求是。”说完,教师才把隐藏的图例显示出来。图例显示红色的直条为女生、蓝色的直条为男生,与学生的猜测正好相反。
赏析:吃一堑方能长一智。首先,这个设计很好地凸显了新知——图例的重要性。复式条形统计图与单式条形统计图的最大区别在于:在同一个统计图中同时呈现不同数量的两种量。如果没有图例加以区分,我们就无法分辨统计的对象,而这正是学生最容易忽视的。教师的做法可谓用心良苦,故意隐藏图例,实则有意挖一个“陷阱”,引诱学生往里面跳,让学生上一回当,接受一次教训,图例的重要性才会在学生的大脑中烙下深深的印记。教师这种故设圈套的教法有助于学生摆脱思维定式,克服惯性思维的负面影响。其次,面对学生的主观臆断,教师巧妙地渗透了严肃认真、实事求是的思想教育。
二、“故弄玄虚”
案例:“平行四边形的面积”教学片段
学生探究平行四边形的面积计算方法时,出现了两种不同的意见:一种意见是用底乘高,另一种意见是用底乘邻边。孰是孰非,教师并没有急于裁判。
“两种做法看起来都有道理,请你们各自说说这样计算的理由,看谁能说服谁。”教师故弄玄虚。
在教师的“唆使”下,学生们的“内讧”开始了。
“我们将平行四边形左边的三角形沿高割下来,平移补到右边,拼成了一个长方形,长方形的长就是平行四边形的底,宽就是平行四边形的高,所以平行四边形的面积等于底乘高。”
“我们将平行四边形拉成长方形,它所有边的长度都没有变化,长方形的长就是平行四边形的底,宽就是平行四边形的斜边,所以平行四边形的面积等于底乘邻边。”
……
两派同学针锋相对,但又苦于拿不出有力的证据,以致出现了认为两种做法都有道理的“两面派”。
“我觉得拉成长方形的做法还是不对。因为将平行四边形两个对角往外拉到一定的程度,就成了一条直线,它的面积肯定变小了。反之,往内拉,它的面积就会变大。”一个学生边说边拿着学具演示。
听他这么一说,很多同学点头认同他的观点。为了使学生看得更清楚,教师将拉扯之前的平行四边形和拉扯之后的长方形的平面图画在一起。
“边的长短没有变化,怎么面积就变大了呢?”教师反问道。
“因为拉成的长方形变高了。”(教师让一学生上台指出变高的那部分)
“那为什么割补成长方形,面积没有变化呢?”教师再次反问道。
“因为割补成长方形后,原来的底和高的长度都没有变化,所以面积就没变。”……至此,持第二种意见的学生才心悦诚服地接受了第一种意见。
赏析:错误也是一种宝贵的资源。对新知学习中出现的错误,教师既不能心太软,也不能心太急,因为教师给予的帮助来得太多、太快,学生的学习过程就被包办得越多,学生从错误中汲取的营养也就越少。解铃还需系铃人,学生只有自己经历了认识错误并改正错误的过程,才能让正确的知识牢牢地根植于自己的头脑之中。就像片段中学生出现的错误,在观点碰撞和思想交锋中,经过辨析、反思、感悟,最终得以改正。这一切归功于教师的“故弄玄虚”。反观我们自己的教学,都希望课堂上能一帆风顺,生怕节外生枝。但面对几十个有着鲜明个性的学生,能做到整齐划一吗?既然不能,为什么不把学生的错误和分歧当成一种资源呢?面对错误,不是教师讲不清,而是不应该替学生讲清,因为我们不能代替学生的思维。既然如此,那我们就留足时间引导学生自己去解决吧。
(作者单位:浏阳市嗣同路小学)
