“平行四边形和梯形”教学研究报告
2016-07-07长沙市高新区明德麓谷学校小学数学组潇湘数学教育工作室
长沙市高新区明德麓谷学校小学数学组 潇湘数学教育工作室
“平行四边形和梯形”教学研究报告
长沙市高新区明德麓谷学校小学数学组 潇湘数学教育工作室
一、问题
“平行四边形和梯形”是一节图形概念教学课,属于空间和图形领域的内容。由于平行四边形、梯形是日常生活中常见的图形,应用也较广泛,学生有一定的辨析平行四边形和梯形的经验,也积累了关于这两种图形的表象,加上对平行、垂直的概念有了一定的认识,这些都为进一步认识平行四边形和梯形打下了良好的知识基础。本课的主要教学目标是:通过对多个图形的辨析,引导学生发现平行四边形和梯形的特征,对图形的本质属性进行归纳,逐步概括出它们的定义,再运用定义辨识图形,给图形分类;体会平行四边形的易变形性;发现四边形中各类图形之间的联系。学生通过这部分知识的学习,为今后学习平行四边形、梯形的面积计算打下基础。那么,如何帮助学生实现从生活经验向数学经验的转化?如何引导学生用正确、简洁的语言概括概念?如何将概念的形成与应用进行顺畅连接?这些都是值得我们研究的问题。
为了更好地了解学生的学情,我们随机抽取四年级57名学生进行了学习前测,下面是前测的统计结果。
(1)辨认平行四边形和梯形
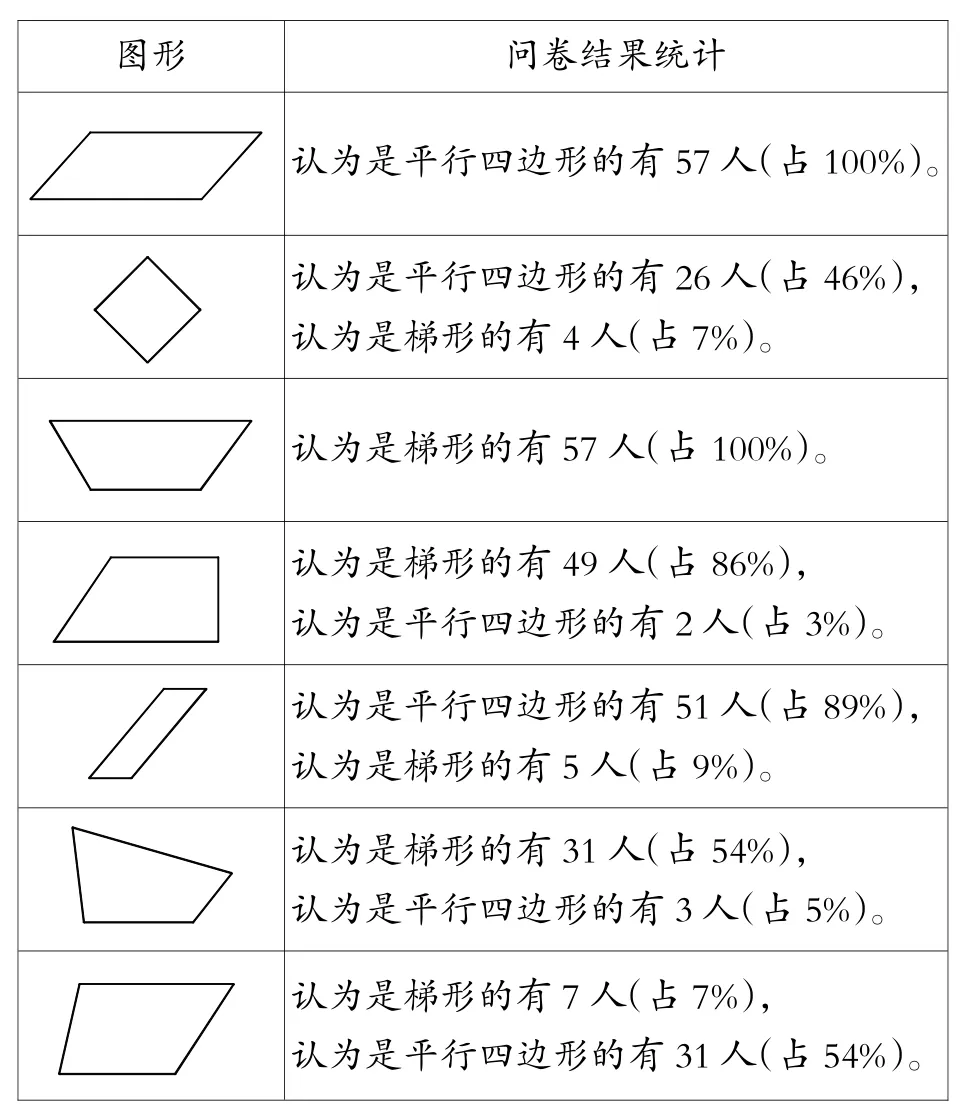
图形 问卷结果统计认为是平行四边形的有57人(占100%)。认为是平行四边形的有26人(占46%),认为是梯形的有4人(占7%)。认为是梯形的有57人(占100%)。认为是梯形的有49人(占86%),认为是平行四边形的有2人(占3%)。认为是平行四边形的有51人(占89%),认为是梯形的有5人(占9%)。认为是梯形的有31人(占54%),认为是平行四边形的有3人(占5%)。认为是梯形的有7人(占7%),认为是平行四边形的有31人(占54%)。
(2)你知道什么是平行四边形吗?它们有什么特点?你知道什么是梯形吗?它们有什么特点?
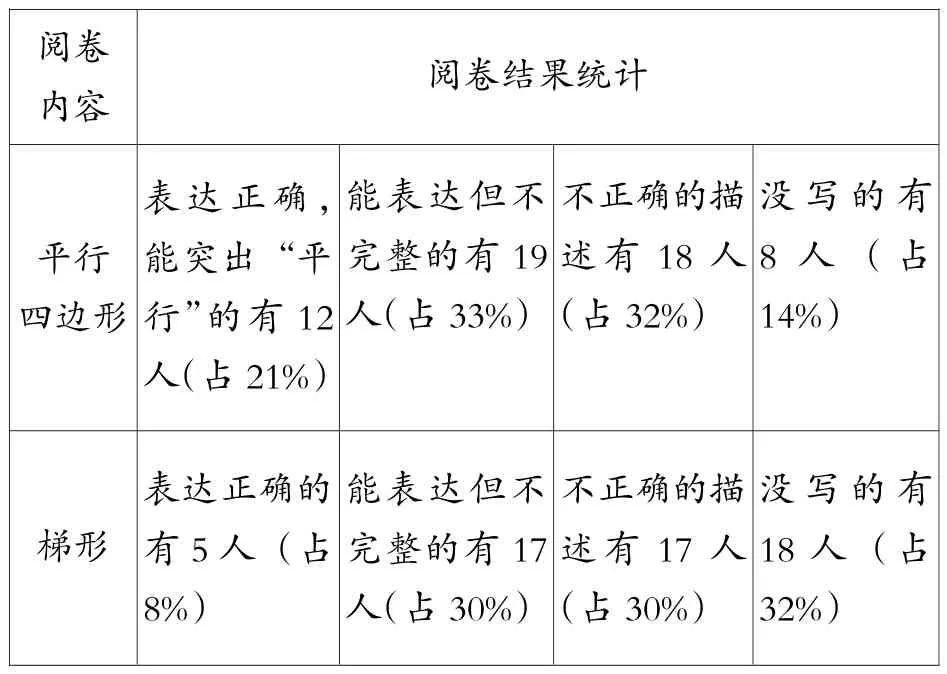
阅卷内容 阅卷结果统计平行四边形表达正确,能突出“平行”的有12人(占21%)能表达但不完整的有19人(占33%)不正确的描述有18人(占32%)没写的有8人(占14%)梯形表达正确的有5人(占8%)能表达但不完整的有17人(占30%)不正确的描述有17人(占30%)没写的有18人(占32%)
(3)你知道四边形、平行四边形、梯形、长方形、正方形之间的关系吗?请用语言或图表示。
调查结果:能用集合图准确表示的有2人(占4%);能用语言较清楚表达的有4人(占8%);零散的表述如“都有4条边”“都有4个角”“内角和都为360度”“都有高”等的有26人(占46%);没写的有25人(占44%)。
1.教学实践中的问题
一方面,学生在三年级初步认识了四边形和平行四边形,通过周长的计算教学进一步了解了长方形和正方形的边的特征。另一方面,本节课中,平行四边形与梯形、四边形的关系以及平行四边形易变形等知识点同时出现,应该如何把握知识的前联后延?针对这些问题,我们将从教与学两个维度加以分析,以期通过研究这些问题,更好地开展教学。
教之困
(1)平行四边形、梯形的知识点多而散,如何整合各个知识点,使知识成体系呈现?
(2)关于平行四边形的概念教学,是教师做好预设,引导学生关注边的位置关系,逐步概括得出概念?还是给学生充分的时间独立探究,在对图形的测量和比较等活动中逐步探索出图形的本质特征,最后概括出概念?哪种方式能使学生对概念掌握得更深刻?
(3)对于梯形的认识,有些学生虽了解了梯形的特征,但总认为同梯子一样的才是梯形,不能接受一些特殊形状的梯形。如何解决学生生活经验带来的负迁移问题?
(4)点子图对认识平行四边形和梯形的特征有什么作用?如何发挥它对学习概念的促进作用,又不束缚学生的思维呢?
(5)我们的教学有三个层次:教知识、教方法、教思想。在平行四边形和梯形的认识教学中,我们除了教给学生有关概念和应用外,还可以教给学生哪些数学思想与方法呢?
学之难
通过观察学生的学习前测结果、访谈对此内容有执教经历的教师、查阅教学后学生的练习检测等,我们发现学生对平行四边形和梯形的学习困惑主要有如下表现——
(1)平行四边形、梯形的概念的建立较单薄、孤立,不能从运动变化等多角度构建四边形的知识网络。
(2)对图形的特征有所理解,但语言表达不是特别准确,容易受概念的非本质属性的干扰。
(3)学生由于没有经历概念的获得过程,或者过程体验不深刻,运用知识解决问题的灵活性不强。
2.对问题的分析
(1)改编整合,关注知识的体系。将教材中原来分开教学的平行四边形和梯形的概念进行整合,让学生对平行四边形和梯形以及一般的四边形有成体系的认识,有利于加深对图形之间关系的理解。
(2)“让学生经历知识获取或知识形成的过程”是当前数学改革提倡的理念。本节课的教学,要给学生充分的时间进行探究、交流,在辨析中发现图形的特征,体验概念的形成过程,将实际操作活动和动画演示相结合,在变与不变的探究过程中体会平行四边形的本质属性。
(3)对有点像平行四边形的“特殊”样子的梯形,在课堂上,教师给予学生充分的时间,运用学到的概念去辨识,不仅可以做到学以致用,还能在学生脑海里留下深刻的印象。
(4)点子图在本课的最大作用是帮助学生发现图形边和角的特点,把点、线、面联系起来,也利于培养学生的空间观念。所以本课教学中可以把握时机,恰到好处地运用点子图。
(5)学生没有经历概念的获得过程,或者过程体验不够深刻,对概念的认识还是停留在表层的文字叙述上,概念的本质属性并没有掌握,也会直接影响概念的运用。和学生一起尝试用准确简洁的语言归纳概念,带学生经历概念的形成过程,对学生以后学习概念的方式方法有指导作用。
二、实践
(一)学生了解抽象概念的方法,体会概念抽象的过程。
片段目标:从对图形的辨析中发现两种图形的特征,抽象出平行四边形和梯形的概念,实现生活经验向数学经验转化。
1.认识平行四边形
师:(课件出示生活中的各种图形)你在图中发现了什么图形?
生1:四边形、平行四边形、梯形等。
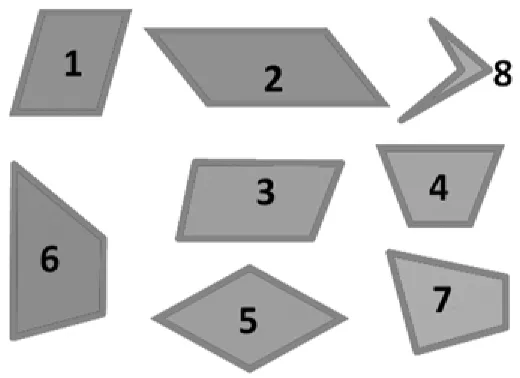
师:这节课我们重点研究四边形中的平行四边形。(板书课题,课件出示8个图形)仔细观察,你能从这些图形中找出平行四边形吗?学生在练习纸上进行图形的探究活动,并汇报。生2:1、2、3、5是平行四边形。(师将图形贴到平行四边形的下面)
生3:我觉得3号图形不像平行四边形。(一部分同学表示同意)
师:既然大家对3号图形有争议,那我们先放一边,来看看别的图形。1、2、5号这3个图形大家认为都是平行四边形,你能说说这些平行四边形都有什么特点吗?
生4:上下两条边相等,左右两条边相等。生5:我能讲得简洁些,对边相等。师:你们怎么发现的?生6:我们用尺子量了。生7:我们学了平行线,这些平行四边形的对边互相平行。
生8:对角也相等,我用量角器测量了。(板书:对边平行、相等,对角相等)
师:为了方便观察,我们可以借助点子图。(出示点子图)仔细观察这3个图,的确具备这些特点。谁来说说到底什么样的四边形是平行四边形?
生9:对边平行而且相等的四边形是平行四边形。生10:还有对角也要相等。
师:我们看看书上怎么说的,是不是和我们说的一样?(生读书上结语)为什么书上只是说“两组对边分别平行的四边形是平行四边形”,而没有说到边的长短和角度?
生11:我们发现只要两组对边都平行,对边就一定会相等。
生12:我画了个图,发现如果有一组对边不平行,就会有对边不相等。要是不平行,那角也不相等了。
师:是的,其实我们在总结什么是平行四边形时,只要说清楚最重要的特点,其他特征就都符合了。(板书:两组对边分别平行的四边形是平行四边形)
2.认识梯形
师:找出了平行四边形,你还能发现什么图形?
生13:我发现4号和6号图是梯形。(师板书,并将两个图贴到梯形下面)
师:梯形又有什么特点?
生14:看点子图,我发现梯形有一组对边平行,另一组对边不平行。(师板书梯形特征)
师:谁能说说什么样的四边形是梯形?
生15:一组对边平行,另一组对边不平行的四边形是梯形。
师:有没有更简洁的说法?
生16:只有一组对边平行的四边形是梯形。(板书)
师:那3号图形到底是什么图形?
生17:我发现3号图形的确不是平行四边形。它有一组对边平行,另一组对边不平行,不符合平行四边形的特点,难道它是梯形?
生18:它不是梯形,梯形有两条边应该往外面打开的,上小下大。
生19:但是它符合梯形的特点,我觉得就是梯形呀!
师:孩子们,其实两条边向外打开的梯形,像梯子的形状,是比较常见的梯形;而像3号这样的图形也叫梯形,也具备梯形的特点,只是它们不常见。
设计意图:利用图形的辨析发现图形的特征,加深对图形的认识。然后尝试概括平行四边形的概念,体会概念的抽象过程。
(二)实际操作和动画演示相结合,在变与不变的探究过程中体会图形的本质属性。
片段目标:探究平行四边形容易变形的特性,了解长方形和正方形是特殊的平行四边形,体会平行四边形易变性在生活中的应用。
教师出示4长4短共8根小棒,让学生拼成一个平行四边形。学生动手拼,并拉一拉。
师:还是平行四边形吗?(再拉一拉)还是吗?(拉成长方形)这时还是平行四边形吗?
生20:还是平行四边形。
生21:和平常见到的平行四边形有点不同,是长方形了。
师:变成长方形后,什么变了?什么没变?

生22(演示):面积变了,边的长短没变,周长没变。
师:对边还平行吗?(借助课件演示)在格子图中,平行四边形拉成长方形,能看出两组对边还是分别平行,对边平行的关系没变。所以长方形、正方形也是平行四边形。现在你们想想,为什么电动门和推拉门要做成平行四边形?(平行四边形容易变形)
设计意图:学生围绕平行四边形变形中的“变”探究:什么变了?什么没变?边的长度没变,周长没变;角的度数变了,面积变了,为学习平行四边形的面积计算做铺垫。
(三)在认识图形的本质属性并建立概念后,用概念辨识图形,经历概念学习的完整过程。
片段目标:利用图形的平移重叠,帮助学生从运动变化的角度巩固所学的知识。
师:我们认识了很多图形,其实图形也会变魔术哦!你信吗?睁大眼睛仔细看。(课件演示两张长方形纸慢慢向中间平移,交叉后出现重叠部分)你能看出中间的重叠部分是什么图形吗?再将一个长方形旋转一下,这时重叠部分又是什么图形?将一个长方形换成三角形,这时的重叠部分又变成什么图形了?再将三角形旋转一下呢?

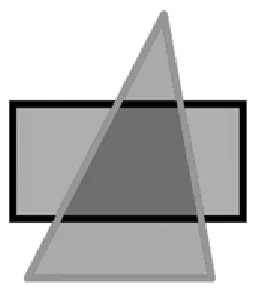
生24:用两个长方形交叉摆放,重叠部分是平行四边形;用三角形和平行四边形交叉放,重叠部分是梯形。
生25:我来补充:因为长方形对边平行,所以中间重叠部分的对边也平行,就是平行四边形;三角形两条边不平行,所以中间重叠部分只有一组对边平行,是梯形。
设计意图:利用图形“变魔术”将学生的注意力聚焦到两个图形的平移运动上。学生用所学的图形的概念或特征辨别图形,学会运用知识解决问题。
三、讨论
这次的教学研究,我们针对教与学中的困惑进行了尝试,有以下一些思考。
1.将两种图形放到一起对比和辨别,有助于概念体系的形成。平行四边形和梯形的概念都是从对边的位置关系中归纳得出的:一般四边形没有一组对边平行,梯形恰有一组对边平行,平行四边形有两组对边平行。将平行四边形和梯形的认识放到一起,学生能更好地理解它们之间以及它们和一般四边形之间的关系。
2.学生经历概念的抽象过程,有利于培养抽象思维能力和归纳概括能力。学生在抽象出图形概念的过程中,需要大量的表象做支撑;在教学图形的概念时,需要借助有趣的活动,让学生在辨析中逐步感受图形的特点,进而认识图形的本质属性,再尝试概括概念。这一教学过程中,应该重本质,轻形式。
3.本课有了完整的概念学习的路径:在辨析中探究图形特征——归纳概括,形成概念——运用概念,再辨识图形。学生学习概念后,能运用概念解决问题,才是真正理解了概念,所以在学生抽象出概念后,应该有一个运用概念解决问题的过程。
4.后续的思考
在教学中,对四边形、平行四边形、梯形、长方形和正方形之间的关系,教师总是习惯于直接告诉学生,“长方形和正方形是特殊的平行四边形,正方形是特殊的长方形”。我们在思考,是否可以从各个图形的特征入手,将图形边和角的特征列举出来,让学生发现图形之间的关系?特征越多,条件越多,这个图形就越特殊;特征越少,条件越少,这类图形就越一般,从而更深切地体会概念的内涵与外延。
平行四边形和梯形其实有很多联系,和长方形、正方形的联系也很紧密。在后面的面积计算的学习中,平行四边形的面积是转化成长方形来计算的;三角形和梯形的面积公式,是由2个完全相同的图形拼成平行四边形,通过计算平行四边形的面积得到的。因此,在本章节的后续学习中是否可以加一节课,让学生借助画图后剪拼或七巧板拼摆等活动体会这几类图形的关系和互变方法,为后续的面积计算学习打好基础?
(执笔:贺慧华、周诚)
