矩形薄板结构的受力分析

唐国策，李敬（.黑龙江飞天建设工程总承包有限责任公司，哈尔滨5000；.中国移动通信集团设计院有限公司黑龙江分公司，哈尔滨5000）



矩形薄板结构的受力分析

唐国策1，李敬2
（1.黑龙江飞天建设工程总承包有限责任公司，哈尔滨150001；2.中国移动通信集团设计院有限公司黑龙江分公司，哈尔滨150001）

摘要：通过根据弹性理论对矩形薄板结构理论分析，建立了薄板结构的几何、物理、平衡关系，在给定构件的边界条件后计算结构的受力和变形情况。通过ANSYS有限元分析软件对四边固支的矩形薄板结构进行了数值模拟，通过算例理论计算结果。由此得出理论计算公式，可以较为准确地在已知设备重量的情况下，求出薄板的跨中最大挠度。

关键词：矩形薄板；数值模拟；受力分析；有限元分析

由于我国通信事业的快速发展，原有的通信机房已经不能满足现有需求，需要对原有结构进行加固后才能正常使用。需要加固的房间多为需要增加电力电池或UPS电池的房间，而在加固这类房间时多使用工字钢作为重量较重的电池支座，并在工字钢上加一层薄钢板以保证整个空间的美观。而当整个空间不全放置电池时，薄钢板上可能放置其他设备，放置设备的重量与薄钢板变形之间的关系是影响整体空间的美观及放置设备稳定性的重要因素。以下通过理论分析及有限元数值模拟，对放置设备的重量与薄钢板变形之间的关系进行了计算，并通过算例对两种方法进行了比较。

1 理论分析

在理论分析时首先做出如下假定：

第一，忽略截面厚度上的弯矩和剪力作用，而只考虑薄板面内的拉应力。

第二，作用的外力可以考虑为流体介质压力，其作用方向与结构内表面垂直。

A'AB'B为四边固支平板矩形结构，a、b分别为短边及长边的边长，在各自的跨中切出单位宽度的板带相交于O'点，ha及hb为受力后O'点宽度和长度方向的跨中挠度。未受外部荷载q作用时，h=h0=0，当外荷载作用后，跨中处的挠度为最大，为了计算外荷载引起的应力σa，σb的大小及其几何量值之间的关系，将外荷载q分解为qa、qb两部分。

根据材料的应力-应变曲线确定其工作阶段的应变值εa，按照σ=Eε或σ=求出σa，若这时已经进入屈服阶段，则

再按照弧长的简化计算公式

求出弧长la，

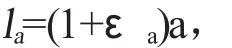
变形曲面投影到宽度a方向的曲线半径

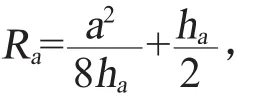
根据εa的值确定

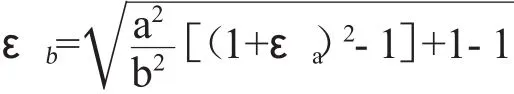
同理可以得到

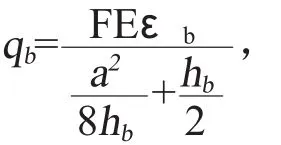
这样就确定了外荷载q的值。

假定h=0.065m，a=0.9m，b=1.6m根据弧长的简化计算公式得到1a=0.9122m，εa=0.0136。可得到Ra= 1.6026m。假定所用材料为Q235钢材，取其σy=240MPa，σu=380MPa，εmax=0.2，求出σa= 249.52 MPa，即可得到qa=311.4kN/m。同理可求得εb= 0.00767，Rb=4.9954m，σb=245.369MPa，即可得到qb=98.2kN/m。因此得到单位长度上的均布荷载压力q=qa+qb=311.4+98.2=409.6kN/m。即单位面积上的均布荷载压力0.4096N/mm2。

2 数值模拟

2.1 前处理及参数设置

第一，选择壳单元SHELL181。

第二，定义材料属性：假定材料为Q235钢板，因此根据Q235钢来确定材料属性。定义材料密度为7 800kg/m3，弹性模量EX=2.06×105N/mm3,泊松比PRXY=0.3，材料的本构关系采用双直线型应力-应变曲线。

第三，根据试件的实际尺寸1 600mm×900mm建立几何模型。

第四，网格化分：考虑到运算速度与求解精度的关系，选择设定网格尺寸为10mm，并选择相应的单元和材料属性，应用Mesh Tool进行网格化分。

第五，施加荷载及边界条件：由于试验中的防护门可近似等效为四边固支的矩形薄板，因此选择限制四个边界的所有自由度，并在每个节点上作用52.5N的集中荷载。

第六，求解：选择求解器，确定分析类型为静力分析，并在分析选项中选取Large Displacement Static，并设定求解载荷步数为100，启动求解器进行求解。

2.2 结果分析

由于本文中是进行静力分析，所以应用POST1查看分析结果。从其变形图中可以看出模型的基本变形形式符合四边固支的薄板结构的受力特性。

由于ANSYS分析时是在每个节点上施加的集中荷载，为了方便与理论值比较，将集中荷载换算成面荷载，

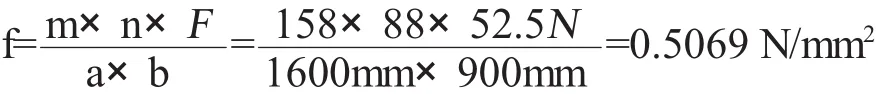
其中f为单位面积上的均布荷载压力，m、n分别是长跨度方向和短跨度方向的网格个数，F为ANSYS分析时所加的集中荷载，a、b分别是长跨度方向和短跨度方向的长度。

3 结论

通过ANSYS有限元静力分析可以试算出，当产生与理论计算假定的变形时，静载为0.5069N/mm2，并通过四边固支薄板结构的受力分析方法，得到了相应的理论解为0.4096N/mm2。由结果可以看出理论解与有限元静力分析的解有一定的差异，其原因在于求解理论解时做出了忽略截面厚度上的弯矩和剪力作用，而只考虑薄板面内的拉应力的基本假定，而ANSYS有限元分析时则考虑了截面厚度上的弯矩及剪力作用。由此得出理论计算公式可以较为准确地在已知设备重量的情况下求出薄板的跨中最大挠度。

参考文献：

［1］曹国雄.弹性矩形薄板振动［M］.北京：中国建筑工业出版社，1983.

［2］张耀春.钢结构设计原理［M］.北京：高等教育出版社，2004.

［3］龙驭球.结构力学［M］.北京：高等教育出版社，2003.

［4］侯和涛，胡肖静，李国强，等.节能复合墙板的极限承载力[J].建筑材料学报，2009，(01):88.

Stress analysis of the rectangular sheet structure

TANGGuo- ce1, LI Jing2
(1.Heilongjiang Feitian Construction General Contractor Co., Ltd., Harbin 150001, China; 2. China Mobile Group Design Institute Co., Ltd., Heilongjiang Branch, Harbin 150001, China)

Abstract:Through theoretical analysis ofrectangular sheet structure based on elastic theory, this paper established balance relationship ofgeometryand physics ofsheet structure which can calculate stress and deformation ofthe structure in a given boundary condition. Making numerical simulation of rectangular sheet by ANSYS finite element analysis software, and calculating the results. It follows that the theoretical formula can calculate maximum deflection of the sheet in the condition of accurately knowing the weight of the equipment.

Key words:Rectangular sheet; Numerical simulation; Stress analysis; Finite element analysis

中图分类号：THl6

文献标志码：A

文章编号：1674- 8646（2016）09- 0010- 02

收稿日期：2016- 01- 25