基于三角级数展开的铣削合力频谱推导及刀具偏心估算

刘　璨　吴敬权　刘焕牢　谭光宇

广东海洋大学,湛江,524088



基于三角级数展开的铣削合力频谱推导及刀具偏心估算

刘璨吴敬权刘焕牢谭光宇

广东海洋大学,湛江,524088

摘要：基于一元切削力机理模型将立铣刀的切削合力分解为公称力和偏心力，采用周期信号的三角级数展开公称力和偏心力，得到其谐波幅值和相位的表达式。基于以上表达式,推导出偶数齿刀具偏心力的偶数次谐波幅值为0，三齿刀具偏心力的刀齿频率谐波幅值也为0。提出了一种用切削合力的主轴和刀齿频率谐波估算刀具偏心距和偏心角的方法，实验结果表明,采用该方法计算出的偏心值接近实测值。从理论上证明了偶数齿刀具的偏心力不存在偶数次谐波成分，所提出的估算方法只需一套估算式和一次切削实验，且数值计算比较容易。研究结果可用于偶数齿刀具的加工过程偏心和磨损辨识及其偏心量估算。

关键词：铣刀;偏心;铣削力;频谱

0引言

铣刀偏心和刀具磨损都将使各个刀齿的切削力不一致。如Schmitz等[1]指出,偏心距为4.9μm的二齿铣刀两个刀齿的切削力峰值大致呈倍数关系。卞荣等[2]认为微细铣刀偏心可能导致单齿切削。Zhang等[3]的研究结果表明,磨损刀齿的切削力将增大。铣刀偏心和刀具磨损对切削力的影响有相似之处，为识别刀具过程状态，有必要提取出偏心的独有特征，并估算偏心尺寸。

以切削厚度为偏心尺寸的函数，Fu等[4]提出了偏心面铣刀的切削力模型；Zheng等[5]提出了偏心面铣刀倾斜铣削的切削厚度模型；Amarego等[6]提出了偏心立铣刀的切削力模型;Li等[7]提出了考虑螺旋角的偏心立铣刀切削力模型；刘璨等[8]推导出偏心立铣刀切削厚度的一种表达式。基于切削力模型,Kline等[9]发现偏心刀具的切削力主轴频率成分显著。Wang等[10]对切削分力作傅立叶变换,发现刀齿倍频±主轴频率处的切削分力成分包含偏心信息，并用切削分力的主轴频率分量和常数项分量估算了偏心尺寸。文献[11-12]在此方法的基础上进一步用优化方法寻找最优估算值。这一方法对二齿和二齿以上的刀具采用不同的估算方程式，且难以解释不同切削分力估算结果的不一致性。Liu等[13]通过模型仿真发现，偶数齿铣刀的偏心力不存在偶数次谐波的现象，并提出了利用这一特点辨识偏心和磨损的新思路，但没有从理论上给予证明。

本文用三角级数展开的方法得到切削合力的频谱表达式，进而从理论上证明了Liu等[13]发现的现象，并提出了应用切削合力的主轴频率和刀齿频率谐波估算偏心距和偏心角的方法。

1偏心刀具的切削力分解

对于齿数为z的立铣刀，若刀具浸入角不大于2π/z，为单齿铣削。图1所示为偏心刀具逆铣时切削平面示意图，其中,O1为主轴旋转中心，O2为刀具物理中心,O1O2为偏心距ρ,β为刀具浸入角。按切削先后顺序对刀齿进行排序，以切削力最大的刀齿为第0刀齿，图1中T0为第0刀齿。α0为偏心方向与T0的夹角,视作刀具偏心角。

在一个主轴旋转周期内,第i刀齿切削时的切削厚度表达式[13]为

(1)

φ=α0-(z+1)π/z

(2)

θi=ωst

(3)

式中,h(θi)为第i齿的切削厚度;ft为每齿进给量;θi为第i齿旋转角;i为刀齿序号,i∈{0,1,…,z-1};ωs为主轴角速度;t为时间变量。

一元切削力模型(lumpedforcemodel)的切削合力与单元刃的切削材料未变形面积成正比。为简化计算,将各刀刃单元的切削厚度作相等处理，则第i个刀齿切削时的切削合力F(θi)的表达式为

F(θi)≈Kh(θi)az

(4)

式中,K为切削力系数;az为切深。

将式(1)代入式(4),得

F(θi)=FN(θi)+FE(θi)

(5)

(6)

(7)

式中,FN(θi)为公称力；FE(θi)为偏心力。

公称力是刀具旋转角的函数，各刀齿的公称力都相同，因此，公称力是以刀齿频率为频率的周期信号。就同一次加工而言,α0和z为常值，若切削用量保持不变,则刀齿号i为偏心力的唯一变量,主轴每旋转一周，刀齿号就变化一个周期，因此，偏心力是与主轴旋转同频率的周期信号。若将FE(θi)的系数2Kρaz归一化为1 N,设α0=-π/6,z=4,β=π/3,则偏心力FE在一个主轴旋转周期内的波形如图2所示。

公称力和偏心力都是周期信号,由多个谐波成分叠加而成，它们可分解为以时间t为变量的公称力FN(t)和偏心力FE(t)：

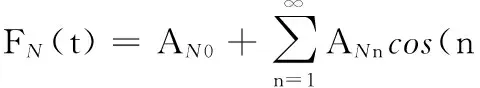
(8)

(9)

其中,AN0、AE0分别为公称力和偏心力的常数项。ANn、AEn分别为公称力和偏心力的n次谐波的幅值。n为谐波次数,n为自然数。ωe为公称力的角速度,等于刀齿频率。ωs为偏心力的角速度,等于主轴旋转的角速度。nωe、nωs分别为公称力和偏心力的n次谐波的圆频率。φNn和φEn分别为公称力和偏心力的n次谐波的相位。ωe和ωs的关系为

ωs=zωe

(10)

2偏心刀具的切削合力频谱表达式、特征

周期信号x(t)可以用三角函数展开式展开：

(11)

(12)

(13)

φn=arctan(bn/an)

(14)

式中,an、bn为三角函数展开式系数;T为x(t)的周期;ω为x(t)的圆频率;An、φn分别为x(t)的n次谐波的幅值和相位。

公称力和偏心力分别是以ωe、ωs为角速度的周期信号，所以可以用三角函数展开式求出其幅值和相位表达式。

2.1公称力的频谱表达式

将式(3)和式(6)代入式(11)、式(12)，得

(15)

(16)

式中,aNn、bNn为公称力的三角函数展开式系数。

将式(15)、式(16)代入式(13)、式(14)，得

(17)

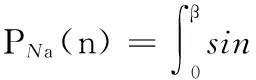
(18)

(19)

(20)

式中,ANn、φNn分别为公称力的n次谐波的幅值和相位。

2.2偏心力的频谱表达式

Ts为偏心力的周期,即刀齿周期。φEn为偏心力的n次谐波的相位。

将式(7)代入式(11)、式(12)，得

aEn=

(21)

(22)

式中,aEn、bEn分别为偏心力的三角函数展开式系数。

将式(21)、式(22)代入式(13)、式(14)，得

(23)

(24)

(25)

(26)

式中,AEn、φEn分别为偏心力的n次谐波的幅值和相位。

2.3切削合力的频谱表达式

因为偏心力的均值为0,其常数项为0,即

AE0=0

(27)

偏心力的基频为主轴频率,公称力的基频为刀齿频率,切削合力的基频为主轴频率。将式(8)、式(9)、式(27)代入式(5)，得

AEncos(nωst+φEn)]

(28)

其中,m=n/z,且m为正整数。式(28)表明，切削合力的常数项等于公称力的常数项。

若n不为z的倍数,则切削合力的第n次谐波只包含偏心力的第n次谐波，其幅值和相位为AEn和φEn。

若n为z的倍数,则由式(28)可得,切削合力的第n次谐波的幅值An和相位φn的表达式为

(29)

(30)

2.4切削合力的频谱特征

2.4.1偶数齿刀具

考虑z和n都为偶数的情况，有

(31)

(32)

由式(24)、式(25)可得

(33)

(34)

将式(31)～式(34)代入式(23)，得

AEn=0

(35)

2.4.2三齿刀具

考虑z=n=3的情况,将z=n=3代入式(23)～式(25)，得

AE3=0

(36)

3刀具偏心尺寸估算方法

立铣刀的齿数z通常大于或等于2,由2.3节的分析可知,切削合力的主轴频率谐波(即1次谐波)等于偏心力的1次谐波。切削合力的n次谐波等于公称力的1次谐波和偏心力的n次谐波之和。可用切削合力的主轴频率谐波(即1次谐波)和刀齿频率谐波(即n次谐波)的幅值和相位代入式(17)～式(20)、式(23)～式(26)、式(29)、式(30)，再采用方程式求解的数值方法求出偏心距ρ和偏心角α0的值。具体估算方法如下：

(1)在铣削过程中采集各切削分力，合成为切削合力。

(2)对切削合力应用FFT算法，求切削合力主轴频率谐波的幅值A1和相位φ1，以及刀齿频率谐波的幅值An和相位φn,AE1=A1,φE1=φ1。

(3)将φ1的值代入式(2)、式(24)～式(26)，求出偏心角α0。

(4)将An、φn的值代入式(17)～式(19)、式(23)～式(25)、式(29)～式(30)，求出偏心距ρ。

根据2.4节的分析结果,对于偶数齿和三齿刀具,其偏心力不存在刀齿频率谐波，即AEz=0,可大大简化偏心距ρ的计算,因此,偶数齿和三齿刀具的偏心尺寸的计算较简单。

4实验

用φ10mm四齿硬质合金立铣刀在铣削加工中心上切削45钢材料。用北京航空航天大学SDC-C4F测力系统(包括应变式测力仪、应变放大器和测力软件)同时测量三个切削分力,测力系统的灵敏度为133.33N/V。逆铣，空气冷却，切削宽度为5mm,主轴转速为1836r/min，进给量和切削深度变化，采样频率为4896Hz。切削参数列于表1。用千分表测得刀具静态偏心距约5.0μm,静态偏心角约45°。

可计算出实验的主轴旋转频率为30.6Hz,4倍频(刀齿频率)为122.4Hz。由实验的加工参数可知,β≈45°。

将实测切削分力合成为切削合力。经滤除50Hz电磁噪声和高于325Hz的成分后，切削合力数据如图3～图6所示。

对各次实验的切削合力数据作快速傅里叶变换处理,得到切削合力的幅频谱和相频谱,其中5号实验的频谱如图7所示。得到各次实验的切削合力的1次谐波的幅值A1、相位φ1以及4次谐波的幅值A4,见表2。

由上文的分析结果可知，A1=AE1,φE1=φ1,A4=AN1。由式(2)、式(17)～式(19)、式(23)～式(26)计算得到各次实验的偏心距和偏心角的估算值，见表2。

5探讨与结论

5.1探讨

如表2所示,当进给量或切削深度较小时，用估算得到的偏心距偏小，这可能是尺寸效应所引起的。本文的估算方法基于切削力系数K为常数,而当进给量或切削深度较小时K不为常数,因此,本文的估算方法适合采用较大的进给量和切削深度。

因偏心力不存在常数项，则A0=AN0,由AE1和A0可求得偏心距ρ的值。对于奇数齿刀具，这种方法比前述方法的计算更简单。然而，切削力系数的尺寸效应对切削合力常数项的作用较大，用该方法将有更大的估算误差。

Wang等[10]也采用了公称力和偏心力频谱的方法估算铣刀偏心尺寸,然而,该方法基于二元切削力机理模型和傅里叶变换,采用x或y向切削分力的常数项和1次谐波估算。而本文的方法基于一元切削力机理模型和周期信号的三角函数展开式，采用切削合力的1次和n次谐波估算。与Wang等[10]的方法相比,本文的方法可降低切削力系数尺寸效应对估算结果的干扰，并且二齿及以上刀具的估算式唯一。

为便于阐述，本文以切入角为0、切出角为β的逆铣为例说明理论推导过程。对于任意的切入角θ1、切出角θ2以及顺铣，都有同样的推导结果，在计算时，用具体的θ1和θ2替代0和β。

5.2结论

(1)由式(35)、式(36)可知，偶数齿刀具和三齿刀具的偏心力的偶数次谐波为0,表明偶数次谐波不存在，这从理论上支持了文献[13]的仿真和实验结果。

(2)从表2可见，各次实验的偏心角估算值之间的偏差小于10°，且与静态偏心角实测值的偏差较小，表明本文提出的立铣刀偏心角估算方法在实验参数范围内有效。

(3)从表2可见，各次实验的偏心距估算值与静态偏心距实测值的相对偏差较小，表明本文提出的立铣刀偏心距估算方法在实验参数范围内有效。

(4)偶数齿刀具的偏心尺寸计算较简单，此外，考虑到尺寸效应的影响，本估算方法更适用于偶数齿刀具，且适合采用较大的进给量和切削深度。

参考文献:

[1]SchmitzTL,CoueyJ,MarshE,etal.RunoutEffectsinMilling:SurfaceFinish,SurfaceLocationError,andStability[J].Int.J.Mach.Tools&Manuf.,2007,47(5):841-851.

[2]卞荣, 何宁, 李亮, 等. 微细铣削氧化锆陶瓷铣削力特征分析[J]. 中国机械工程, 2014, 25(23): 3200-3206.

BianRong,HeNing,LiLiang,etal.AnalysisonCharacteristicsofMillingForceinMicro-millingofZrO2Ceramics[J].ChinaMechanicalEngineering,2014,25(23):3200-3206.

[3]ZhangS,LiJF,SunJ,etal.ToolWearandCuttingForcesVariationinHigh-speedEnd-millingTi-6Al-4VAlloy[J].InternationalJournalofAdvancedManufacturingTechnology,2010,46(1/4): 69-78.

[4]FuHJ,DevorRE,KapoorSG.AMechanisticModelforthePredictionoftheForceSysteminFaceMillingOperations[J].ASMEJ.Eng.Ind.,1984,106(1):81-88.

[5]ZhengHQ,LiXP,WongYS,etal.TheoreticalModelingandSimulationofCuttingForcesinFaceMillingwithCutterRunout[J].Int.J.Mach.Tools&Manuf.,1999,39(12):2003-2018.

[6]AmaregoEJA,DesphandeNP.ComputerizedPredictiveCuttingModelsforForcesinEndMillingIncludingEccentricityEffects[J].AnnalsofCIRP,1989,38(1):45-49.

[7]LiXP,LiHZ.TheoreticalModelingofCuttingForcesinHelicalEndMillingwithCutterRunout[J].InternationalJournalofMechanicalSciences,2004,46(9):1399-1414.

[8]刘璨,吴敬权,李广慧,等.基于单刃铣削力峰值的铣刀偏心辨识[J].机械工程学报, 2013,49(1):185-190.

LiuCan,WuJingquan,LiGuanghui,etal.IdentificationofMillsEccentricityBasedonPeakForceofSingleEdge[J].JournalofMechanicalEngineering,2013,49(1):185-190.

[9]KlineWA,DevorRE.TheEffectofRunoutonCuttingGeometryandForcesinEndMilling[J].Int.J.Mach.ToolDes. &Res.,1983,23(2/3):123-140.

[10]WangJJJ,ZhengCM.IdentificationofCutterOffsetinEndMillingwithoutaPriorKnowledgeofCuttingCoefficients[J].InternationalJournalofMachineTools&Manufacutre,2003,43(7):687-697.

[11]WanM,ZhangWH.SystematicStudyonCuttingForceModelingMethodsforPeripheralMilling[J].Int.J.ofMach.Tools&Manuf.,2009,49(5):424-432.

[12]刘显波, 龙新华, 孟光,等.基于频域多目标优化的铣削力系数及偏心参数识别[J].机械工程学报, 2011,47(7):185-190.

LiuXianbo,LongXinhua,MengGuang,etal.TheIdentificationsofMillingForceCoefficientsandEccentricityBasedonMulti-objectiveOptimizationinFrequency-domain[J].JournalofMechanicalEngineering,2011,47(7):185-190.

[13]LiuC,WuJQ,LiGH,etal.Frequency-spectrumCharacteristicsofForceinEndMillingwithToolWearandEccentricity[J].Int.J.Adv.Manuf.Technol.,2013,67(1/4):925-938.

(编辑陈勇)

SpectralDerivationofResultantMillingForceandEccentricEstimationofToolBasedonTrigonometricSeriesExpansion

LiuCanWuJingquanLiuHuanlaoTanGuangyu

GuangdongOceanUniversity,Zhanjiang,Guangdong,524088

Keywords:millingcutter;eccentricity;millingforce;frequencyspectrum

Abstract:Thecuttingforcewasdiscomposedintonominalandeccentriccomponentforcesbasedonunarycuttingforcemodel,thetrigonometricseriesofperiodicsignalswasappliedtoexpandthesetwocomponentforces，andthentheamplitudeandphaseexpressionsoftheirharmonicswereobtained.Basedontheseexpressions,itisdeducedthattheeven-harmonicsamplitudesoftheeccentricforceforeven-toothmillingcutterarezero,thetooth-frequencyamplitudeoftheeccentricforcefor3teethmillingcuttersiszerotoo,andanewestimationmethodofeccentricdistanceandangleformillingcutterswaspresented,whichusestheharmonicsofresultantcuttingforceinspindleandtoothfrequencies,theestimatedeccentricvaluesareclosetothatmeasuredinexperiments.Ittestifiesintheorythattherearenoevenharmonicsintheeccentriccomponentforceofeven-toothmillingcutters,thepresentedmethodneedsonlyonesetofequationandonecuttingtest,anditsnumericalcalculationisrathereasyforeven-toothmillingcutters.Theresearchfruitscanbeusedtoidentifyeccentricityandwear,andestimateeccentricityinprocessforeven-toothmillingcutters.

收稿日期：2015-04-14

基金项目：国家自然科学基金资助项目(51375099，51375100)

作者简介：刘璨，男，1971年生。广东海洋大学工程学院副教授、博士。主要研究方向为机械加工过程的监测控制。吴敬权，男，1980年生。广东海洋大学工程学院实验员。刘焕牢，男，1967年生。广东海洋大学工程学院教授、博士。谭光宇(通信作者),男,1957年生。广东海洋大学工程学院教授、博士。

中图分类号：TH161

DOI：10.3969/j.issn.1004-132X.2016.02.017