旋转机械运行稳定性劣化的高阶累积量特征提取方法

蒋章雷　徐小力

北京信息科技大学现代测控技术教育部重点实验室，北京，100192



旋转机械运行稳定性劣化的高阶累积量特征提取方法

蒋章雷徐小力

北京信息科技大学现代测控技术教育部重点实验室，北京，100192

摘要：研究了基于高阶累积量理论的1.5维谱、四阶累积量对角切片谱方法在提取运行稳定性劣化特征方面的性能;从敏感性、趋势性、差异性、一致性角度，讨论了两种特征提取方法的趋势预测适用性。基于构建的转子实验台进行转子系统多种劣化类型下不同劣化程度状态的特征提取实验,检验两种方法作为特征提取手段的性能,解决了风电机组传动系统运行稳定性劣化的状态诊断、劣化趋势预测中特征提取方法的选择缺少理论依据的问题。

关键词：风电机组；稳定性劣化；1.5维谱；四阶累积量对角切片谱；特征提取

0引言

我国一直鼓励、支持风电等战略性新兴产业的发展，《能源发展“十二五”规划》中提出大力发展风能等可再生能源，加快风能资源的分散开发利用[1]。《风电发展“十二五”规划》中提出:加快风电产业技术升级，提高风电的技术性能和产品质量，使风电成为具有较强国际竞争力的重要战略性新兴产业[2]。

随着风电机组的建设和运行，风电机组故障数量逐年增加，由此造成的经济损失越来越严重。风电机组传动系统包括传动轴、齿轮箱等，是风电机组故障多发部件[3]，从一系列公开发表的资料和文献来看，其状态诊断及趋势预测研究日益成为国内外学者研究的热点，而特征提取方法是研究的难点[4-6]。高阶累积量是解决非线性、非平稳、非高斯、非最小相位、非因果信号的主要手段，利用高阶累积量理论提取不同于传统时频分析方法的信号特征已成为机电设备状态诊断研究中的一项重要内容[7-8]。

本文将高阶累积量理论应用于运行稳定性劣化特征提取，考察高阶累积量方法作为特征提取手段的性能，解决风电机组传动系统运行稳定性劣化的状态诊断、劣化趋势预测中特征提取方法的选择缺少理论依据的问题。

1高阶累积量的基本理论

1.1高阶累积量的定义

高阶累计量是指阶数大于2的累计量,包括高阶累积量、高阶累积量谱等。

令单个随机变量x具有概率密度f(x),定义其第一特征函数如下：

(1)

定义单个随机变量x的累积量生成函数(第二特征函数)如下：

ψ(ω)=lnΦ(ω)

(2)

定义单个随机变量x的k阶累积量为第二特征函数的k阶导数在原点的值：

(3)

将单个随机变量的高阶累积量定义进行推广,得到随机向量的高阶矩与高阶累积量的定义[9]:

令x=(x1,x2,…,xk)T是一随机向量,且ω=(ω1,ω2,…,ωk),则随机向量的第一特征函数为Φ(ω1,ω2,…,ωk)=E{ej(ω1x1+ω2x2+…+ωkωk)},对其求r=v1+v2+…+vk次偏导数,则有

(4)

若令ω1=ω2…=ωk=0,则由式(4)得到随机向量x的r阶矩的定义：

(5)

参照随机变量的第二特征函数定义,得到随机向量的第二特征函数：

ψ(ω1,ω2,…,ωk)=lnΦ(ω1,ω2,…,ωk)

(6)

则随机向量的r阶累积量定义为

(7)

其中,v1+v2+…+vk=r,特别地，取v1=v2=…=vk=1,得到k阶矩和k阶累积量，记作:mk=m1,1…,1=mom(x1,x2,…,xk),ck=c1,1,…,1=cum(x1,x2,…,xk)。

设数列{x(n)}为零均值k阶平稳随机过程，则其k阶矩定义为

mkx(τ1,τ2,…,τk-1)=mom(x(n),x(n+τ1),

…,x(n+τn-1))

(8)

式中,τ1,τ2,…,τk-1为延时。

其k阶累积量定义为

mkx(τ1,τ2,…,τk-1)=cum(x(n),

x(n+τ1),…,x(n+τn-1))

(9)

1.2高阶累积量谱的定义

理论上,高斯过程大于二阶的累积量谱为零,而非零累积量谱提供了一种非高斯性度量，因此工程上通常以高阶累积量谱作为分析非高斯随机过程的主要数学工具[9-10]。

若式(9)中高阶累积量ckx(τ1,τ2,…,τk-1)是绝对可和的，即

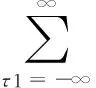
(10)

则k阶累积量谱定义为k阶累积量的k-1维Fourier变换，即

(11)

根据式(9),三阶累积量定义为

c3x(τ1,τ2)=cum(x(n),x(n+τ1)，x(n+τ2))

(12)

根据式(11)，三阶累积量谱定义为

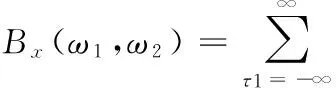
(13)

习惯上，高阶累积量谱简称高阶谱或多谱，我们称三阶谱为双谱，称四阶谱为三谱。特别地,S2x(ω)称为数列{x(n)}的功率谱。

2运行稳定性劣化的高阶累积量特征提取方法

高阶累积量及其高阶累积量谱是多维函数，维数的增加将导致计算复杂性大大提高，在对实际信号作高阶累积量估计时，多维的累积量计算起来非常复杂；同时对于三维以上的数据体难以用图形进行表示，因此必须降低高阶累积量的维数。Mendel[11]提出利用高阶累积量一维片段及其一维Fourier变换作为从高阶累积量中提取有用信息的方法,即对高阶累积量作切片处理，以降低高阶累积量及其高阶累积量谱的维数,这主要包括1.5维谱以及四阶累积量对角切片谱方法。

2.11.5维谱的定义及性质分析

考虑一个非高斯平稳随机过程x(n),它的三阶累积量为c3x(τ1,τ2)=cum(x(n),x(n+τ1),x(n+τ2)),定义三阶累积量一维切片为

(14)

式(14)称为三阶累积量一维对角切片[12]。

定义三阶累积量一维对角切片谱为

(15)

式(15)为三阶累积量一维对角切片的一维Fourier变换,定义为三阶累积量对角切片谱，或称为1.5维谱。

1.5维谱方法仅使用了三阶累积量的对角线切片，而且只进行了一维Fourier变换，因此可以大大减小计算量。

2.2四阶累积量对角切片谱的定义及性质分析

一个非高斯平稳过程x(n)的四阶累积量的一维切片定义如下：

(16)

x(n)的四阶累积量的对角切片C4x(τ,τ,τ)的Fourier变换,定义为x(n)的四阶累积量对角切片谱：

(17)

3高阶累积量特征提取方法的劣化特征提取性能实验

风电机组传动系统故障大部分是传动系统的趋势性故障，都会经历发生、发展直至恶化的阶段，其状态劣化过程对应着各个劣化状态之间的迁移过程。为了准确描述劣化状态之间的迁移过程，找到状态劣化发展趋势与劣化特征之间的对应关系，需要模拟传动系统的多种劣化类型，每一种劣化类型下需要包含不同劣化程度状态。为进行风场风电机组难以实施的各种劣化实验，基于典型传动形式构建转子实验台。

设置转子系统多种劣化类型下不同劣化程度状态，并采集振动数据。劣化类型包括：转子不平衡状态、基础松动状态、动静碰摩状态、转子不平衡与动静碰摩的耦合故障状态、基础松动与动静碰摩的耦合故障状态、转子不平衡与基础松动的耦合故障状态等，每种劣化类型下包含不同的劣化程度。

3.1实验设备及实验数据的采集

实验数据采集现场如图1所示，转子转速设定为1700 r/min,以近似模拟额定风速下某型风电机组齿轮箱输出轴的转速；数据采集系统选用丹麦B&K公司的PULSE系统,采集仪型号为3050-B-060,为六通道数据采集仪;通过加速度振动传感器采集振动信号,传感器型号为INV9832A,为三向加速度振动传感器;采样频率设定为10 240 Hz,每组振动数据包含2048个采样点。

3.1.1转子正常、转子不平衡运行状态

转子不平衡是风电机组中较常见的一种故障状态[13],故设置转子多个不平衡运行状态进行模拟实验。转子上固定有旋转圆盘，圆盘沿圆周均布着16个圆孔，通过在圆孔中拧入不同数量的配重螺钉实现转子不平衡状态下不同劣化程度的模拟：分别将两个、四个、六个配重螺钉拧入旋转圆盘，设定此时转子状态分别为轻度、中度、重度不平衡。给出每种状态下各自旋入配重螺钉的总质量与旋转圆盘质量的百分比，以此作为不平衡劣化程度的度量标准，见表1。通过实验得到转子正常运行状态、不平衡劣化类型下不同劣化程度状态的振动数据。

3.1.2基础松动状态

松动故障会使机械系统出现偏心而产生不平衡力,当不平衡力超过重力时,机器就会被不平衡力周期性地抬起,导致机械系统出现更严重的故障状态[14]。松动转子实验台上轴承座支撑架与底座的紧固螺钉，以减小支撑结构弹性刚度，模拟基础松动状态。将轴承座支撑架的一个紧固螺钉旋松一圈代表轻度基础松动状态；将紧固螺钉旋松两圈代表中度基础松动状态。采集得到基础松动状态下不同劣化程度状态的振动数据。

3.1.3动静碰摩状态

动静碰摩除了引起转子、定子之间的间隙增大,轴承支承磨损之外,更重要的是会引发转轴不稳定的反进动,导致接触面上产生很大的法向力和摩擦力,转子的反向涡动不收敛，反向涡动转速迅速增大,最终引发旋转机械的严重损坏[14]。在转子实验台中利用一个顶杆来进行动静碰摩实验[15],将动静件碰摩定性地分成四个阶段：刚开始碰摩、早期尖锐型触碰、中期半尖锐型碰摩和晚期平钝型碰摩,动静碰摩原理图如图2a所示。选择在转子实验台上固定一个可以旋入碰摩块的支撑架，碰摩块与转轴之间的间隙可通过螺纹调整，如图2b所示，其中，最左侧支撑架为可以旋入碰摩块的支撑架。

设置动静碰摩不同劣化程度的两个状态,将刚开始碰摩到早期尖锐型触碰作为轻度动静碰摩状态,将早期尖锐型触碰到中期半尖锐型碰摩作为中度动静碰摩状态,采集转子系统振动信号。

3.1.4耦合故障

在转子系统实际运行中,两种或者两种以上形式的故障有可能同时出现，即出现耦合故障，耦合故障的存在,会增加转子系统故障诊断、趋势预测的复杂性。

设置转子轻度不平衡与轻度动静碰摩状态为耦合故障轻度状态；中度不平衡与中度动静碰摩状态为耦合故障中度状态。同理，设置转子不平衡与基础松动的耦合故障的轻度与中度状态、动静碰摩与基础松动的耦合故障的轻度与中度状态。采集每种状态下的振动信号。

3.2特征提取方法的劣化特征提取性能分析

应用1.5维谱、四阶累积量对角切片谱方法对传动系统多种劣化类型不同劣化程度数据进行特征提取处理，显示特征提取结果，得到其劣化特征谱图。通过特征谱图分析不同特征提取方法的劣化特征提取性能。

作为劣化特征提取性能的分析依据，本文提出如下判断特征提取方法对于状态劣化是否具有差异性、一致性、敏感性、趋势性的标准：

(1)依据系统在正常运行状态下与不同劣化类型下的特征谱图是否具有明显区别，作为判断特征提取方法是否具有差异性的标准。

(2)依据同一种劣化类型下不同劣化程度的特征谱图中谱峰分布形态是否相似，作为判断特征提取方法是否具有一致性的标准。

(3)依据特征谱图中最大峰值在系统由正常运行状态迁移到轻度劣化状态时变化是否显著，作为判断特征提取方法对状态劣化是否具有敏感性的标准。

(4)依据特征谱图中最大峰值是否随着劣化程度的增大而不断增大，能否表现出趋势性信息,作为判断特征提取方法对系统由正常运行状态到逐渐劣化的全过程是否具有趋势性的标准。

显然,若特征提取方法对于状态劣化具有差异性、一致性，则这种方法适合用于劣化类型的诊断研究；若特征提取方法对于状态劣化具有敏感性、趋势性，则这种方法适合用于运行稳定性劣化趋势的预测研究。

3.2.11.5维谱劣化特征提取性能分析

单一劣化类型的劣化特征提取。对转子正常运行状态、不平衡运行状态的振动数据进行基于1.5维谱的特征提取操作，得到转子相关运行状态的特征谱图,如图3～图10所示。

由图3～图10的特征谱图可知：

(1)图4所示转子正常状态特征谱图中最大峰值位于224 Hz处，幅值为1942；图6所示轻度不平衡状态特征谱图中最大峰值位于224 Hz处,幅值急剧增大至4519。最大峰值在系统由正常状态劣化到轻度不平衡状态时变化十分显著,表明1.5维谱特征提取方法对状态劣化具有敏感性,这有利于揭示系统早期劣化进程。

(2)在转子不平衡状态特征谱图的最大峰值明显变化的同时，谱峰的分布形态并未出现明显变化，表明同一种劣化类型下的劣化特征具有一致性，这为风电机组传动系统的状态诊断研究提供了良好基础。

(3)随着转子系统不平衡状态的劣化,最大峰值经历了4519→5071→5505的变化,最大峰值均出现在224 Hz附近。转子系统同一劣化类型下不同劣化程度的最大峰值存在明显的趋势性。

(4)转子系统正常状态下频率成分比较单一,劣化到不平衡状态后,谱图中低频部分与高频部分的峰值数量明显增多,出现了多谱峰现象。正常运行状态下的特征谱图与不平衡运行状态下的特征谱图具有明显的差异性。

对基础松动状态数据、动静碰摩状态数据进行特征提取,结果表明,系统出现轻度劣化后，特征谱图中峰值数值变化明显，特征提取方法对系统由正常运行状态迁移到轻度劣化状态具有敏感性；同种劣化类型下不同劣化程度的特征谱图具有一致性；系统由正常运行状态逐渐劣化的过程能够表现出趋势性。同时，转子正常运行状态特征谱图中谱峰分布形态与不同劣化类型下特征谱图中谱峰分布形态具有比较明显的差异性。

耦合劣化类型的劣化特征提取。利用1.5维谱特征提取方法对转子轻度不平衡耦合轻度基础松动状态、转子中度不平衡耦合中度基础松动状态下的数据进行特征提取操作，得到图11、图12。

由转子系统正常运行状态下的特征谱图及图11、图12可看出：

(1)随着转子系统由正常运行状态劣化到耦合故障轻度状态,特征谱图中最大峰值由1942(位于224 Hz处)减小到1762(位于208 Hz处),这表明该特征提取方法对于系统耦合劣化状态的敏感性低于单一劣化状态的敏感性。

(2)特征谱图中谱峰的分布形态不尽相同：转子系统正常状态的特征谱图只有一个明显波峰;耦合故障中度劣化谱图出现了多个波峰，表明对于耦合故障类型，该方法提取的劣化特征的一致性低于单一劣化类型的一致性。

(3)随着转子系统逐渐劣化，特征谱图中最大峰值随着劣化程度的增加呈现不断减小的趋势，这表明，耦合故障状态下不同劣化程度的最大峰值的趋势性与劣化程度的趋势性相反。

分析不平衡耦合动静碰摩状态、动静碰摩耦合基础松动状态的特征谱图，结果表明：当耦合故障状态中某个单一劣化类型占主要成分时,该特征提取方法对于状态劣化的敏感性、一致性有所提高。

3.2.2四阶累积量对角切片谱劣化特征提取性能分析

三阶累积量是三阶中心矩,描述了概率分布的非对称性；四阶累积量是任意随机变量的矩与正态随机变量的同阶矩的差，描述了概率分布相比正态分布平坦或者尖锐的程度[16]。考虑到四阶累积量能够揭示不同于三阶累积量的信息，因此继续考察四阶累积量对角切片谱特征提取方法的性能。

(1)单一劣化类型的劣化特征提取。对转子正常、不平衡状态振动数据进行四阶累积量对角切片谱操作，得到各状态的谱图，如图13～图16所示。

由图13～图16可知：谱图中最大峰值在系统由正常运行状态劣化到轻度不平衡状态时变化显著，表明四阶累积量对角切片谱特征提取方法对于系统状态劣化具有敏感性；不同劣化程度的谱图中谱线的分布形态相似，且谱图表现出的频率成份较为单一，表明同一种劣化类型下的劣化特征具有一致性；谱图中最大峰值变化为：435→939→1575.3→705，可见随着不平衡状态的逐渐劣化，最大峰值没有表现出确定的趋势性信息。

对基础松动状态、动静碰摩状态的特征提取的研究结果表明，该特征提取方法对系统正常运行状态、不同劣化类型状态能够表现出一定的差异性；对系统由正常运行状态迁移到轻度劣化状态具有敏感性；同种劣化类型下不同劣化程度的谱图具有一致性；对系统由正常运行状态逐渐劣化的全过程没有表现出趋势性。

(2)耦合劣化类型的劣化特征提取。对轻度不平衡耦合轻度基础松动状态、中度不平衡耦合中度基础松动状态的振动数据进行四阶累积量对角切片谱操作，得到两种状态的四阶累积量对角切片谱图，如图17、图18所示。

由转子正常运行状态的谱图及图17、图18可知：四阶累积量对角切片谱方法对于系统状态劣化具有一定的敏感性；同种劣化类型下的特征谱图分布形态具有一致性；不具有表征状态劣化的趋势性；具有比较明显的差异性。

3.3特征提取方法的趋势预测适用性讨论

针对多种劣化类型下不同劣化程度状态数据，基于1.5维谱和四阶累积量对角切片谱方法进行了特征提取分析，得到了两种特征提取方法对状态劣化的差异性、一致性、敏感性、趋势性信息，见表2，其中方法1、2分别代表1.5维谱、四阶累积量对角切片谱。

从两种特征提取方法对于状态劣化的敏感性、趋势性、差异性、一致性的角度来讨论这两种特征提取方法作为稳定性劣化趋势预测的适用性[17-18]。

(1)对于单一劣化类型，1.5维谱特征提取方法与四阶累积对角切片谱特征提取方法都具有良好的差异性、一致性,因此可以考虑融合两种特征提取方法进行单一劣化类型状态的诊断研究;1.5维谱方法在敏感性、趋势性方面的性能要优于四阶累积对角切片谱方法，因此可以利用1.5维谱方法进行稳定性劣化趋势预测。

(2)对于耦合劣化类型,四阶累积对角切片谱特征提取方法在差异性、一致性方面的性能要优于1.5维谱特征提取方法,因此可以利用四阶累积对角切片谱方法进行耦合劣化类型状态的诊断研究;1.5维谱与四阶累积对角切片谱方法都不具有敏感性、趋势性，因此这两种方法都不适合用于耦合劣化类型稳定性劣化趋势预测。

4结语

本文针对风电机组变工况、非平稳运行特点，研究了1.5维谱以及四阶累积量对角切片谱方法用于特征提取的性能，基于敏感性、趋势性、差异性、一致性衡量了特征提取方法的趋势预测适用性，为风电机组传动系统运行稳定性劣化的状态诊断、劣化趋势预测中特征提取方法的选择提供了理论依据。

参考文献:

[1]能源发展“十二五”规划[R].北京: 国家能源局, 2013.

[2]风电发展“十二五”规划[R].北京:国家能源局,2012.

[3]Johan R,Margareta B L.Survey of Failures in Wind Power Systems with Focus on Swedish Wind Power Plants during 1997-2005[J].IEEE Transactions on Energy Conversion,2007,22(1):167-173.

[4]王国彪,何正嘉,陈雪峰，等.机械故障诊断基础研究“何去何从”[J].机械工程学报,2013,49(1): 63-72.

Wang Guobiao, He Zhengjia, Chen Xuefeng,et al. Basic Research on Machinery Fault Diagnosis-What Is the Prescription [J]. Journal of Mechanical Engineering, 2013,49(1): 63-72.

[5]于传洋,许宝杰,吴国新,等.一种风电机组的故障预测算法[J].北京信息科技大学学报,2013,28(4)：35-38.

Yu Chuanyang, Xu Baojie, Wu Guoxin,et al. A Fault Prediction Algorithm of Wind Turbine Generator[J].Journal of Beijing Information Science and Technology University, 2013,28(4): 35-38.

[6]王红军,左云波.基于局部线性降维拓扑空间的主轴故障诊断方法[J].北京信息科技大学学报, 2014,29(2):35-38.

Wang Hongjun, ZuoYunbo. Spindle Fault Diagnosis Method Based on Logal Linear Dimension Reduction Topological Space[J]. Journal of Beijing Information Science and Technology University, 2013,28(4):35-38.

[7]Montero F E H,Medina O C.The Application of Bispectrum on Diagnosis of Rolling Element Bearings:A Theoretical Approach[J].Mechanical Systems and Signal Processing,2008,22(3):588-596.

[8]Zhou Y,Chen J,Dong G M, et al. Application of the Horizontal Slice of Cyclicbispectrum in Rolling Element Bearings Diagnosis[J].Mechanical Systems and Signal Processing,2012,26(1):229-243.

[9]张贤达.时间序列分析——高阶统计量方法[M].北京:清华大学出版社,1996.

[10]邱天爽,张旭秀,李小兵,等.统计信号处理——非高斯信号处理及其应用[M].北京:电子工业出版社,2004.

[11]Mendel J M.Tutorial on Higher-order Statistics(Spectra) in Signal Processing and System Theory Theoretical Results and Some Application[J].Proceedings of the IEEE,1991，79(3):278-305.

[12]Nikias C L,Mendel J M.Signal Processing with Higher-order Spectra[J].IEEE Signal Processing Magazine,1993,10(3):10-37.

[13]Villa L F,Renones A,Peran J R,et al.Statistical Fault Diagnosis Based on Vibration Analysis for Gear Test-bench under Non-stationary Conditions of Speed and Load[J].Mechanical Systems and Signal Processing,2012,29(5):436-446.

[14]闻邦椿,武新华,丁千,等.故障旋转机械非线性动力学的理论与试验[M].北京:科学出版社,2004.

[15]胡茑庆,张雨,刘耀宗,等.转子系统动静件间尖锐碰摩时的振动特征试验研究[J].中国机械工程,2002,13(9): 777-780.

Hu Yuanqing,Zhang Yu,Liu Yaozong,et al.Experiment Research on Vibration Characteristics of Sharp Rup-impact between Rotor and Stator of a Rotor System[J]. China Mechanical Engineering,2002,13(9): 777-780.

[16]王书明,朱培民,李宏伟,等.地球物理学中的高阶统计量方法[M].北京:科学出版社,2006.

[17]左云波,王西彬,徐小力.DFAR模型在旋转机械故障预测中的应用[J].中国机械工程,2009,20(12):1460-1463.

Zuo Yunbo,Wang Xibin,Xu Xiaoli.Application of DFAR Model to the Trend Prediction of Fault in Rotary Machines[J].China Mechanical Engineering,2009,20(12):1460-1463.

[18]蒋章雷,徐小力.旋转机械运行稳定性劣化的1.5维谱特征提取方法[J].中国机械工程,2015,26(23):3208-3213.

Jiang Zhanglei,Xu Xiaoli.Feature Extraction Method of 1.5-dimensional Faced to Running Stability Deterioration of Rotating Machinery[J].China Mechanical Engineering,2015,26(23):3208-3213.

(编辑陈勇)

Feature Extraction Method Based on High Order Cumulant Faced to Running Stability Deterioration of Rotating Machinery

Jiang ZhangleiXu Xiaoli

Key Laboratory of Modern Measurement & Control Technology,Ministry of Education,Beijing Information Science and Technology University,Beijing,100192

Key words:wind turbine;stability deterioration;1.5-dimension spectrum;fourth-order cumulant diagonal slice spectrum;feature extraction

Abstract:This paper focused on feature extraction method based on high order cumulant like 1.5-dimension spectrum and fourth-order cumulant diagonal slice spectrum,and also its performance on running stability deterioration.Experimental data of varying degrees of deterioration under various types of deterioration were collected,and sensitivity property,trend property,difference property,and consistency property were proposed to evaluate different methods.It can provide theoretical basis for selecting feature extraction method for fault diagnosis and trend prediction of running stability deterioration.

收稿日期：2015-04-09

基金项目：国家自然科学基金资助项目(51275052);北京市自然科学基金资助重点项目(3131002);北京市教委科研计划资助重点项目(KZ201311232036);现代测控技术教育部重点实验室开放课题资助项目(KF20141123202)

作者简介：蒋章雷,男,1983年生。北京信息科技大学现代测控技术教育部重点实验室助理研究员、博士。主要研究方向为机电装备运行状态监控检测技术。发表论文10余篇。徐小力，男,1951年生。北京信息科技大学现代测控技术教育部重点实验室教授、博士研究生导师。

中图分类号：TH17

DOI：10.3969/j.issn.1004-132X.2016.02.004