基于单杆矢量的机构复合分离位置函数综合

王成志　张全明　王淑可　周　球　代　婷

1.集美大学,厦门,361021　　2.福建省永安市林业局,永安,366000



基于单杆矢量的机构复合分离位置函数综合

王成志1张全明1王淑可2周球1代婷1

1.集美大学,厦门,3610212.福建省永安市林业局,永安,366000

摘要：提出用单杆相对运动差单元构建平面机构函数综合方程式。首先建立单杆的相对位置运动差及高阶运动差通用单杆矢量公式,再通过引入变量和增加单杆矢量附加方程,消除了方程式中非独立的未知角变量及未知高阶角变量。然后用单杆矢量及其附加方程直接建立有限分离、无限接近分离及复合分离位置函数综合的统一通用的多项式方程组，且方程总次数低。讨论了在平面铰链四杆机构函数综合中的复合五位置问题及复合四位置问题上的应用，用实例计算了“实现函数”与“预期函数”的误差并作出误差波动图，结果表明在无限分离精确点及无限接近分离点上可以精确实现预期函数，但按高阶运动特性要求设计的机构不一定能使“实现函数”在所有0阶位置上更逼近“预期函数”。该方法比双杆组、三杆组法简单，模块性非常好，便于计算机自动建模与求解。

关键词：相对运动理论；单杆矢量；函数综合;复合分离位置;同伦法

0引言

刚体导引、函数生成和轨迹生成精确点运动综合代数法中,目前主要采用位移矩阵结合杆-副约束[1-5]和矢量环法结合双杆组(dyad)[6-7]、三杆组(triad)[8-9]组合推导,建立机构位置综合方程。以上方法几乎成为推导机构运动综合方程的标准方法,其他的还有几何代数化法,如转动极代数化法[10-12]等。新提出的方法有同向坐标法(isotropiccoordinates)[13]、指数法[14]等。一般情况下,将得到的位置综合方程对时间或输入参数求导,就得到了高阶综合方程，不同运动特性的搭配构成了有限分离位置、无限接近分离位置和复合分离位置(或混合“点阶”)问题[12,15](为了讨论方便,本文将这三类综合统一称为复合位置问题)。由于高阶综合相对复杂些,故讨论有限分离位置综合的文献比较多。在函数生成综合中,文献[1,2,9,16]讨论了有限分离位置函数综合;文献[17]根据相对运动转换法“刚化”四杆机构，将函数综合问题转化为刚体导引综合问题进行研究;文献[11-12]用相对极代数化法比较完整地分析了四杆机构函数综合的有限分离位置、无限接近分离位置和复合点阶分离位置问题，但没有给出五位置问题的方程，都是用求两条四位置问题的Burmester曲线的交点来解决四杆机构五位置函数综合问题。另外，双杆组法和三杆组法虽然可以获得比较低的多重齐次化Bezout数[18],但对兴趣点到机架所连接的杆数有限制，这在一定程度上限制了它们的应用。

本文提出用相对运动差建立运动综合方程,推导出的通用单杆矢量(monad)方程可以直接用来建立机构有限分离位置、无限接近分离位置和复合分离位置问题的五位置和四位置综合问题的方程。同时,通过建立单杆矢量分量相互关系的附加方程,技巧性地消除了三角函数,降低了求解非线性方程所需要跟踪的同伦路径数,在计算效率与保证模块性及通用性上找到了一种较好的折中方法。

1基本原理

1.1相对位置差

考虑图1中做平面运动的刚体Ω上A、B两点的运动(两点连线用矢量z1表示)。当刚体从位置1运动到位置j时,刚体转动了θ1j角,A、B两点分别从点A1、B1运动到了点Aj、Bj(两点连线用矢量zj表示)。如图1所示，有

(1)

Δz=z1j=zj-z1

其中,Δz是扣除A点的运动后(或者说,B点相对A点)B点在位置j相对位置1的位移差。将矢量z1j称为B点相对A点的相对位移差,或者称为位移单杆矢量。

如果把A点称为牵连点,B点称为兴趣点,则式(1)表明：兴趣点的位置差等于牵连点的位置差与B点相对A点的相对位移差的矢量和。例如,图2所示的铰链四杆机构,按式(1),当连杆机构从位置1运动到位置j时，由杆a、z组成的O1A1B1开环在B点的相对位移为

δB1j=δO11j+a1j+z1j=a1j+z1j

(2)

因O1是固定铰链,所以有δO11j=0。

同理，还可以列出由杆c组成的O2B1开环在B点的相对位移表达式。O1A1B1环和O2B1环在B点铰接在一起运动，因此,在连杆机构从初始位置1运动到位置j时，O1A1B1环在B点的相对位移差等于O2B1环在B点的相对位移差,即

a1j+z1j=c1j

(3)

显见,可以用这种相对位移关系建立机构有限分离位置的综合方程。

1.2相对高阶运动差

按照运动学理论，图1中刚体Ω在位置j时，兴趣点的n阶时间导数等于牵连点Aj的n阶导数与Bj点相对Aj点的n阶导数的矢量和。即

(4)

其中,在英文字母或希腊字母上标位置括号中的数字，表示该字母所代表的量对时间或对输入变量求导的次数。

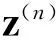
1.3通用相对运动关系式

综上所述,如果多个刚体用运动副连接并与机架相连,则输出构件上输出点相对机架的位置差等于机架到输出构件之间几个构件相对位移差的矢量和。例如，若一个开环由任意个矢量zi(i=1,2,…)组成,则开环末端点P相对机架的任意阶导数相对运动差为

(5)

式(5)表明,机构中各单杆矢量的相对运动差决定了参考点P输出运动的增量。显然，要根据分离位置点来运用式(5)。为了便于后文讨论，先明确以下两个概念。

一个在平面上的实际物理位置点j称为有限分离位置点。每两个有限分离位置,只能列出一个位置关系式。所以，式(5)中，当n=0时,j改成1j,则表示位置j(j>1)相对初始位置1；而1个位置j与1个“阶数”n(n≠0)的组合,其几何意义实际是两个位置无限接近。但由于这种组合只能用式(5)列出一个n阶导数关系式,所以将其称为位置j(j=1,2,…)上的1个无限接近分离位置。在1个实际有限分离位置点j上可以有多个无限接近分离位置。例如,对P1P2-P3P4P5情形，有2个有限分离位置点(即j=1,2),3个无限接近分离位置(其中,j=1时，n=0,1，有一个无限接近分离位置;j=2时，n=0,1,2,有2个无限接近分离位置)。用J表示综合问题中的有限分离位置总数,N表示无限接近分离位置总数。

由于单自由度机构函数综合中，常给出的是输入与输出构件的转角关系且输入杆匀速转动，而且在高阶函数综合中，给定的输入输出函数关系不一定是时间导数的关系，而可能是输出变量对输入变量的导数关系。所以，后文中各参数是对输入变量求导数。

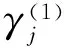
2单杆矢量基本公式

从上文中可以发现,本文是利用单杆的相对运动差建立综合方程的。容易推导出刚体上A、B两点长度不变时,各阶导数的单杆矢量通用公式(含0阶)：

(6)

位移单杠矢量的公式推导过程为

(7)

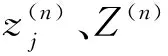
(8)

两变量与原参数的关系用增加一个附加位移约束方程来表示：

(9)

高阶单杆矢量的分量及其对应的附加方程见表2。显见,一个单杆矢量分量式要新增两个分量变量和一个方程。如果用分量式代入式(5)，则自然就消除了式(5)中的三角函数。笔者将这种消除方程中的三角函数的方法称为2变元修正法。

3四杆机构复合位置函数综合

3.1综合方程

对于图2的铰链四杆机构，可以将式(3)扩展为n阶函数综合方程：

(10)

即

(11)

式(11)有未知角变量的三角函数，增加了求解的复杂性。用数值同伦法求解方程时，处理未知角变量三角函数的方法主要有以下几种：①直接法[19]。即直接将角位移当一个变量使用;②1变元法。即每个角度引入一个变量t[20]，用三角函数的万能代换公式：t=tan(γ/2)，sinγ=2t/(1+t2)和cosγ=(1-t2)/(1+t2)消除方程中的三角函数；③2变元法。即每个角度引入两个变量x、y(x=cosγ,y=sinγ),再对应增加一个方程x2+y2=1；④消除未知角度变量法。 即分别列出未知角变量的正弦和余弦表达式，然后利用cos2γ+sin2γ=1消除角度变量γ。目前双杆组法[6]和三杆组法[8-9]等都采用方法4。例如,用方法④消除式(11)中的角度变量γ1j,得到铰链四杆机构函数综合的三杆组通用综合公式：

(12)

Aj=1-cosθ1jBj=sinθ1j

Cj=cosθ1j+cosψ1j-1-cos(θ1j-ψ1j)

Dj=sinθ1j-sinψ1j-sin(θ1j-ψ1j)

Ej=sinψ1jFj=1-cosψ1j

则四杆机构复合位置函数综合方程组由J-1+N个式(12)组成。方程组的6个未知变量分别是ax、ay、zx、zy、cx、cy。

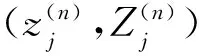
(13)

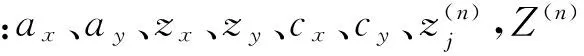
(14)

注意:如果机架d杆长及角度σ已知,则zx=dcosσ+cx-ax，zy=dsinσ+cy-ay可代入式(12)和式(13)中，表2中0阶的附加方程可改为

(dsinσ+cy-ay)2=0

(15)

比较式(12)和式(13)可以发现,式(13)推导简单方便,而且式(13)及其附加方程非常规整,模块性和通用性都非常好,便于计算机自动建立综合方程。同时，式(12) 限制所连接杆的数目是3，而单杆矢量法理论上可应用于任意复杂机构的建模(当然，如果用同伦法求解，则会受到计算时间的限制)。

3.2方程组总次数分析

式(11)的次数为n+2(在初始位置1时,是n+1次)。即:导数的阶数n越高，方程的次数越高。当为4阶导数时，是6次方程(在初始位置1时，是5次方程)。所以不同类型的复合位置综合，方程组总次数不同；式(12)的次数固定为2，综合方程组的总次数TD=2J+N-1;而用本文方法提出的式(13)是线性的,每个附加方程的次数都是2。所以，其总次数与引入附加方程的个数有关。若J+N个位置综合的机构中有K个杆的转角未知(四杆机构函数综合时K=1)，则要引入K(J+N-1)个附加方程。所以,方程组的总次数TD=2K(J+N-1)。

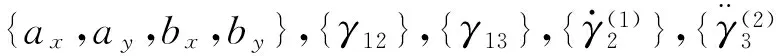
从表3可以看出,前三种方法(直接法、2变元法和1变元法)TD和BN值都比较大(其中,直接法与2变元法的TD和BN值相同,且前三种方法的BN值都相同)，而且对于不同复合位置情形，齐次化后方程组的BN值各不相同。第四种方法(即杆组法)BN值最小,但模块性有所降低。本文提出的2变元修正法直接消除了非独立角变量的三角函数,特别是还消除了非独立的高阶角变量，而前3种方法是没有办法直接消除高阶角变量的。本方法的总次数明显少于前三种方法，与杆组法得到的综合方程组在齐次化前的总次数TD相同。

总之,本方法构造的各种复合位置综合方程具有相同的方程结构，而且同伦路径数相同，所以，便于计算机自动构造初始方程，从而方便计算机自动求解。

3.3五位置综合问题

按前文讨论,只要满足J+N=5，就是复合五位置问题。这时式(13)及对应的附加方程的数目正好与未知变量的数目相等。

四杆机构复合五位置综合的组合数总共有16种情形。取不同的j和n组合重复式(13)四次,加上对应的附加方程4个，就可作为这16种复合分离位置情形的综合方程组。如前所述，方程组总次数TD=2K(J+N-1)=16，即用同伦法求解方程组要跟踪16条路径。

例1:分别按表3中的5种复合五位置综合情形设计铰链四杆机构，实现给定的函数y=ex-0.5x1.1(0.5≤x≤1.5)及其相应的导数函数。其中，输入、输出连架杆的最大摆角均为60°。

在给定的x区间，由各综合情形需要的有限分离位置按Chebyshev公式选精确点,并将要实现的函数转换为对应的转角关系，如表4所示。用同伦法求解前面讨论的综合方程组，最多有4组解。对本题预期函数，每种情形都只有一组有效的实数解(还有1组退化解、2组非实数解)，见表5。定义以下相对误差百分比：

(16)式中,y为要实现的“预期函数”值;Y为用铰链四杆机构实现的角位移转换为原来的y=f(x)关系后的“实现函数”值。

给定区间内各阶导数的相对误差百分比波动情况见图3(由于P1P2P3P4P5情形只有一个有限分离点，因此，没有画出其相对误差图)。图3的第一列图形是单纯0阶情况下的相对误差百分比波动情况，其最大值列于表5最后1行。

图3例1中各综合情形下相对误差百分比波动情况

从图3可以看出,精确综合在有限分离精确点上和在无限接近分离位置点上，确实分别精确满足其要求的0阶和高阶导数函数关系。但区间内的其他点只是近似满足0阶或高阶导数函数关系。这与有关文献的结果一致。另外，观察表5最后一行或图3的第一列图，也就是只对比0阶情况下“预期函数”与“实现函数”之间的误差，发现无限接近位置数越多，或者说导数的阶数越高，其0阶函数在区间内的最大误差并不一定会越小。例如，P1-P2P3P4P5含3阶导数逼近，但其0阶函数(即位置函数)的误差比前三种情形的误差更大。因此，如果只有位置要求，不必对机构盲目要求高阶运动特性。

3.4四位置综合问题

若J+N=4,就是复合四位置问题。四杆机构中,将不同的j及n组合，总共有8种复合四位置情形。取不同j及n重复式(13)三次,加上对应的3个附加方程,得到由9个方程组成的方程组,总次数为TD=2J+N-1=8,即复合四位置问题用同伦法求解要跟踪8条路径。但方程组有10个未知变量。可以在ax,ay,cx,cy中任选一个作为自由变量。可以假设ax=acosθ1,ay=asinθ1(0≤θ1≤180°),式(13)变成

(17)

当θ1变化时,将求得的ax,ay,cx,cy转化为动铰链点A、B的轨迹，就是Burmester圆点曲线。可以证明θ1在0°～180°区间变化求出的ax,ay,cx,cy值，与在180°～360°区间变化求出的值相同。因此，θ1∈[0°,180°]。

例2:按例1的函数关系画出实现PPPP(无限接近四分离位置)情形的Burmester圆点曲线。

为了与例1的结果对比，从复合五位置问题的5个位置(含无限接近位置)中选出4个位置来构成复合四位置问题。5个无限接近分离位置可以组合成4组无限接近四位置情形(有限分离情形下有5组),用Tesar标记法[15]大致表示为P1P2P3P4、P1P2P3P5、P1P2P4P5、P1P3P4P5。这种标记法显然有些模糊。笔者建议的标记方法是：分别用D(Displacement)、V(Velocity)、A(Acceleration)、J(Jerk)和S(Snap)字母分别代表0阶、1阶、2阶、3阶、4阶导数的方程，下标表示方程对应的有限分离位置。例如，上述4种组合情形可以分别表示为：V1A1J1、V1A1S1、V1J1S1和A1J1S1。这种表示方法含义比Tesar标记法更清晰。该标记法应用的其他例子见表4第一栏。

图4所示为在情形V1A1J1、V1A1S1下动铰链点A和B的Burmester圆点曲线(按d=1,σ=0°)。图中曲线上标记点附近的数值表示θ1的角度值(单位为“度”)。

也可以用求两条或多条复合四位置问题的Burmester曲线的交点来求解复合五位置问题[11-12]。例如，图4中的四杆机构O1A1B1O2就是例1中P1P2P3P4P5(V1A1J1S1)情形的解。其中，A1点是两条圆点曲线AV1A1J1、AV1A1S1的交点，其x、y坐标就是机构的ax、ay；而B1点是另两条圆点曲线BV1A1J1、BV1A1S1的交点，将其x、y坐标减去机架d在x、y轴上的投影就是机构的cx、cy。这个结果与表5中的P1P2P3P4P5情形的结果完全相同。在图4中,交点O1和O2是该问题的退化解。注意，只有所有可能的四位置Burmester曲线以相同对应的θ1角度值通过的共同交点，才是所要求的机构解。否则可能只是极点或镜点。同样，A、B圆点曲线上具有相同θ1值的动铰链点才能配对成两个动铰链。

4结语

(1)将0阶与高阶的相对运动公式合并为一个通用相对运动公式，得到了输出点的各阶导数的相对运动差等于组成开链中各相应阶导数单杆矢量的矢量和。建立了可用于有限分离、无限接近分离和复合分离位置问题的通用机构综合方程。

(2)单杆矢量有矩阵式和分量式，分别用于已知杆转角和未知杆转角的场合。用单杆矢量分量以及增加附加方程的方式，可以消除方程中的非独立的未知角变量及未知高阶角变量，简化方程结构。增加的各种阶数的附加方程也非常简单且结构相似。用同伦法求解时，可以构建相同结构的初始方程组。

(3)本方法得到的方程组总次数，明显低于其他方法,而与用双杆组或三杆组法得到的方程组总次数相同。但本方法用非常简单的过程就达到简化方程的目的。当然，本方法的总次数还高于双杆组或三杆组法采用齐次化后得到Bezout数。

(4)直接用杆的单杆矢量列方程，模块性好，方便用计算机自动建模与求解，便于编写通用的机构设计软件。理论上要比双杆组或三杆组法更容易建立任意复杂机构运动综合方程。当然，复杂机构最好是单杆与双杆组或三杆组联合使用。

(5)本方法得到的综合方程组也可再简化，得到双杆组或三杆组方程。

(6)无限接近位置数越多，或者说导数的阶数越高，其0阶函数在区间内的最大误差并不一定会越小。

本文试图找到一种模块性好、通用性好，但同伦路径数又不至于过大的一种新方法。根据上面的分析，单杆矢量法具有这方面的特点。文中举例讨论了在铰链四杆机构复合五位置和复合四位置函数综合问题中的应用。另外，本文讨论的公式也可推广到刚体导引和轨迹生成的机构综合问题。而且，从理论上来说，本方法也可用于复杂机构，但求方程组全部解的时间将会非常长。当然，除可用系数同伦法减少跟踪路径外,还可考虑用云计算形式来缩短计算时间。笔者用多核计算机进行并行计算，发现求解计算时间可明显缩短。

参考文献:

[1]SuhCH,RadeliffeCW.SynthesisofPlaneLinkagewithUseoftheDisplacementMatrix[J].ASMEJournalofEngineeringforIndustry, 1967,89(2):206-241.

[2]DhingraAK,ChengJC,KohliD.SynthesisofSix-link,Slider-crankandFour-linkMechanismsforFunction,PathandMotionGenerationUsingHomotopywithM-homogenization[J].JournalofMechanicalDesign,1994,116(4): 1122-1131.

[3]黄昔光, 廖启征, 魏世民,等. 基于代数法的平面四杆机构五精确点轨迹综合[J].北京邮电大学学报，

2008, 31(2):1-4.

HuangXiguang,LiaoQizheng,WeiShimin,etal.FivePrecisionPointsPathSynthesisofPlanarFour-barLinkageUsingAlgebraicMethod[J].JournalofBeijingUniversityofPostsandTelecommunications,2008,31(2):1-4.

[4]田忠辉，王淑芬. 基于位移矩阵的平面四杆机构运动综合[J]. 大连大学学报,2010(6):57-60.

TianZhonghui,WangShufen.TheKineticSynthesisofPlaneFourBarMechanismBasedonDisplacementMatrix[J].JournalofDalianUniversity, 2010(6):57-60.

[5]韩建友, 崔光珍, 杨通. 六杆机构四位置运动生成的解域综合理论与方法[J]. 北京航空航天大学学报,2014,40(9): 1170-1175.

HanJianyou,CuiGuangzhen,YangTong.SolutionRegionSynthesisTheoryandMethodofSix-barLinkageswith4-positionMotionGeneration[J].JournalofBeijingUniversityofAeronauticsandAstronautics,2014,40(9): 1170-1175.

[6]ErdmanAG.ThreeandFourPrecisionPointKinematicSynthesisofPlanarLinkages[J].MechanismandMachineTheory,1981,16(3): 227-245.

[7]ChenChao,BaiShaoping,JorgeA.TheSynthesisofDyadswithOnePrismaticJoint[J].JournalofMechanicalDesign,2008,130(3):034501-1-6.

[8]ChaseTR,ErdmanAG,RileyDR.TriadSynthesisforUptoFiveDesignPositionswithApplicationtotheDesignofArbitraryPlanarMechanisms[J].JournalofMechanisms,Transmissions,andAutomationinDesign, 1987, 109(4): 426-434.

[9]SubbianT,FlugradJrDR.FivePositionTriadSynthesiswithApplicationstoFour-andSix-barMechanisms[J].JournalofMechanicalDesign, 1993,115(2): 262-268.

[10]付金元, 陈永. 刚体导引的平面四杆机构综合的新解法[J]. 机械工程学报,1996,32(2):40-46.

FuJinyuan,ChenYong.NewApproachfortheSynthesisofPlanarPathGenerators[J].ChineseJournalofMechanicalEngineering，1996,32(2): 40-46.

[11]ChiangCH.SynthesisofFour-barFunctionGeneratorsbyMeansofEquationsofThreeRelativePoles—1.FinitelySeparatedPositions[J].MechanismandMachineTheory,1975,10(1):81-91.

[12]ChiangCH.SynthesisofFour-barFunctionGeneratorsbyMeansofEquationsofThreeRelativePoles—2.Mixed“Point-order”Synthesis[J].MechanismandMachineTheory,1975,10(1):93-109.

[13]PlecnikMM,McCarthyJM.NumericalSynthesisofSix-barLinkagesforMechanicalComputation[J].JournalofMechanismsandRobotics, 2014,6(3): 031012-1-12.

[14]PerezA,McCarthyJM.CliffordAlgebraExponentialsandPlanarLinkageSynthesisEquations[J].JournalofMechanicalDesign, 2005, 127(5): 931-940.

[15]TesarD,SparksJW.TheGeneralizedConceptofFiveMultiplySeparatedPositionsinCoplanarMotion[J].JournalofMechanisms, 1968, 3(1): 25-33.

[16]杨廷力.机械系统基本理论:结构学、运动学、动力学[M].北京:机械工业出版社,1996.

[17]钱卫香, 韩建友. 实现连架杆给定角位移的机构综合方法[J]. 农业机械学报, 2009,40(5):222-226.

QianWeixiang,HanJianyou.SynthesisMethodforPlanarFour-barLinkagesGivenAngleDisplacementsofRotatingLinks[J].TransactionsoftheChineseSocietyofAgriculturalMachinery,2009,40(5):222-226.

[18]WamplerCW,MorganAP,SommeseAJ.NumericalContinuationMethodsforSolvingPolynomialSystemsArisinginKinematics[J].JournalofMechanicalDesign,1990,112(1):59-68.

[19]DongBo,YuBo.HomotopyMethodforSolvingMixedTrigonometricPolynomialSystems[J].JournalofInformationandComputationalScience,2007,4(2):505-513.

[20]廖启征.连杆机构运动学几何代数求解综述[J].北京邮电大学学报, 2010,33(4):1-11.

LiaoQizheng.GeometryAlgebraMethodforSolvingtheKinematicsofLinkageMechanisms[J].JournalofBeijingUniversityofPostsandTelecommunications,2010,33(4):1-11.

(编辑陈勇)

MultiplySeparatedPositionSynthesisofFunctionGenerationMechanismBasedonMonadVectors

WangChengzhi1ZhangQuanming1WangShuke2ZhouQiu1DaiTing1

1.JimeiUniversity,Xiamen,Fujian,3610212.ForestryBureauofYongan,Yong’an,Fujian,366000

Keywords:relativemotiontheory;monadvector;functiongeneration;multiplyseparatedposition;homotopymethod

Abstract:Therelativemotiondifferencesofthemonadswerepresentedtomodelthesystemsofequationsforkinematicfunctionsynthesisofplanarlinkages.Theuniformformulaeoftherelativemotiondifferenceswith0-ordertohigher-orderderivativeswereconstructedfirstly,andthenthenewvariablesandcorrespondingspecialauxiliaryequationsofthemonadvectorswereusedtoeliminatetrigonometricfunction,theangularunknownsandeventheirhigherorderangularunknowns.Themonadvectorsandtheircorrespondingauxiliaryequationscouldbedirectlyusedtoconstructsynthesissystemsforfinitely,infinitesimallyandmultiplyseparatedprecisionpositions,andthesystemswerepolynomialequationswithsmallervaluesofthetotaldegrees.Applyingtheformulaetofiveandfourmultiplyseparatedpositionsoffunctionsynthesisforpin-jointedfour-barplanarlinkageswasdiscussed.Somecasesofthemultiplyseparatedpositionswereexemplifiedandtheirdifferencesbetweenthegeneratedy-valueandrequiredy-valuewerecalculatedandcharted.Theresultsshowthatthepositionsatfinitelyandinfinitesimallyseparatedpositionswerepassedthroughexactlyaccordingtotherequiredfunction.However,they-valuesgeneratedbythemechanismwiththehigher-orderfunctionalrequirementsmaybenomoreclosetotherequiredy-valuethanthosegeneratedbythemechanismwiththelower-orderfunctionalrequirementsatall0-orderpositionsintherequiredrange.Theprocedureissimplerandtheformulaeofmonadhavethebettermodularitythanthedyadandtriad,andcanbeeasilyadaptedtoautomaticmodelingandsolvingtheequationsinacomputer.

收稿日期：2014-09-28

基金项目：福建省自然科学基金资助项目(2012J01225)

作者简介：王成志,男,1962年生。集美大学机械与能源工程学院教授。主要研究方向为机构学、CAD、科学计算可视化、光学测量。张全明，男，1967年生。集美大学机械与能源工程学院副教授。王淑可，女，1972年生。福建省永安市林业局高级工程师。周球,男,1992年生。集美大学机械与能源工程学院硕士研究生。代婷,女,1990年生。集美大学机械与能源工程学院硕士研究生。

中图分类号：TH112.1

DOI：10.3969/j.issn.1004-132X.2016.02.008