落球冲击破碎下的非限制料层夹持形态

毛亚郎　孙　毅　计时鸣　单继宏　金晓航

浙江工业大学，杭州，310014



落球冲击破碎下的非限制料层夹持形态

毛亚郎孙毅计时鸣单继宏金晓航

浙江工业大学，杭州，310014

摘要：为提高球磨粉碎的效率，构建了球形介质对非限制料层的冲击粉碎模型，开展了落球冲击破碎下的料层夹持形态研究。通过石英砂料层的落球冲击破碎实验，分析了初始料层厚度、落球冲击能量、冲击速度、落球大小以及料层颗粒大小对料层夹持形态的影响。实验结果表明，夹持颗粒完全破碎时，料层夹持厚度为2层颗粒的堆叠厚度情况下，夹持范围受落球大小和夹持角度的影响较大。根据夹持角度与安息角的关联性，建立了料层夹持半径与落球大小、安息角的数学模型。

关键词：落球冲击；非限制料层；夹持厚度；夹持范围

0引言

在矿石、水泥、陶瓷等大规模粉体加工中，球形介质冲击料层是颗粒的主要破碎方式[1-3]。料层受球形介质冲击时，颗粒处于非限制状态，会快速滑移和飞溅，仅少量被夹持颗粒得以破碎。被夹持颗粒的数量与料层的夹持形态(夹持厚度、夹持范围)密切相关[4]，直接影响料层破碎质量和冲击破碎效率[5]。因此有必要建立非限制料层夹持形态的数学模型，构建料层破碎模型以提高粉磨效率。

非限制料层的静态挤压实验表明，受球形介质大小和颗粒粒度的影响，石英砂料层的夹持厚度约为1～3层颗粒的堆叠厚度[6]。非限制料层的冲击破碎实验表明，初始料层层数大于2时，颗粒的破碎质量保持不变[7]。Bourgeois[8]认为，料层颗粒只有被推挤到底层时才会被夹持破碎，提出了单层料层颗粒夹持面积计算公式。Barrios等[9]进一步分析了颗粒粒度、冲击能量、落球直径和料层排布对单层料层夹持面积的影响，但落球冲击下料层颗粒的破碎并不完全是单层料层夹持破碎[10-11]。笔者利用石英砂的落球冲击破碎实验分析了初始料层厚度、落球冲击能量、落球直径和颗粒粒度对多层料层夹持厚度和范围的影响，以构建非限制料层夹持形态的数学模型。

1非限制料层的夹持形态

落球对料层的夹持范围是以球心投影为中心的圆域，整个料层的夹持形态呈圆柱状[9]，如图1所示。当落球的冲击能量足以将夹持范围内颗粒完全破碎时，料层的夹持质量与破碎质量相等，通过实验可以获得冲击破碎质量：

(1)

式中，ρ为料层堆叠密度；hn为夹持厚度；rn为夹持半径。

由图1可得夹持半径：

rn=Dsinα/2

(2)

式中，D为落球直径；α为夹持角度。

因落球冲击料层的持续时间极短[6]，且可能存在颗粒飞溅，故料层夹持厚度和夹持范围的直接检测比较困难。笔者以常见的石英砂料层颗粒为破碎对象，通过分析颗粒破碎质量及其影响因素，间接建立了料层夹持厚度和夹持半径的数学模型。

2非限制料层落球冲击破碎实验

2.1实验装置

非限制料层落球冲击破碎实验装置如图2所示。钢球从预定高度沿着竖直的空心导柱下落冲击铁砧上的料层，收集被冲击的料层颗粒以分析破碎情况。装置的围板用于收集飞溅的颗粒，细线用于提升钢球，导向柱可使落球冲击后保持原位，减少落球滚动造成的二次破碎，便于对颗粒破碎形态的观察。

实验前，将石英砂颗粒进行筛分并称重，以确定被冲击料层颗粒粒度和数量。将实验颗粒在圆筒内轻压铺平后，移除圆筒得到非限制料层。收集单次冲击后的颗粒进行定时振动筛分，得到小于初始粒度大小的破碎颗粒，用精度为0.01 g电子称计重，同样的实验过程重复3次，取平均值。

2.2实验项目与结果

针对影响颗粒破碎质量的因素(初始料层厚度、冲击高度、冲击能量、落球大小和颗粒大小)，开展了5项单因素落球实验。落球直径根据球磨机钢球直径半理论公式计算[12]：

(3)

式中，Kc为量纲一的综合修正系数；φ为磨机转速率；σb为颗粒单轴抗压强度，kg/cm2；ρe为钢球的有效密度,kg/cm3；D0为球磨机筒体直径，mm；d为颗粒粒径，mm。

石英砂颗粒选取较大粒径以利于筛选和观察，初始料层范围为直径50 mm圆域。

3实验结果分析

3.1料层夹持厚度分析

对初始料层厚度为1～5 mm的料层开展了冲击破碎实验(实验1)，其中，石英砂颗粒粒径d=0.85 mm，根据式(3)计算得到钢球直径D=25 mm。为保证夹持料层内颗粒能够完全破碎，采用较大落球高度(H=265 mm)。实验1得到破碎质量随初始料层厚度的变化如图3所示。在相同的冲击能量下，单层料层(料层厚度为1 mm)的破碎质量小于多层料层的破碎质量。料层层数大于2(料层厚度大于2 mm)时，破碎质量趋于稳定；初始料层较厚时，受冲击能量的影响，破碎质量略有下降。可见在冲击能量充足时，多层料层的厚度对破碎质量的影响很小。Bourgeois[8]以120 mm的落球高度，80 mm钢球直径，对粒度为4.00～4.75 mm石英砂料层进行了冲击实验，得出了相近的结果，Göll等[11]的落球实验也得出了当料层数大于2时，破碎质量不再增大的结论。因此可确定落球冲击破碎下的非限制料层夹持厚度为2层颗粒的堆叠厚度，即hn=2d。

3.2落球高度与冲击能量的影响

对冲击高度在60～400 mm的多层料层开展了落球冲击破碎实验(实验2)，其中，料层高度h=3 mm，钢球直径和颗粒直径与实验1相同。结合实验2获得的破碎质量随落球高度的变化曲线(图4)和不同冲击高度下未飞溅颗粒的破碎形态(图5)，可将料层破碎分为两个阶段：第一阶段(H为60～150 mm)为低冲击能量阶段，夹持颗粒未完全破碎，破碎质量随着冲击高度的增大而显著增大，这种情况不适合采用破碎质量来分析夹持半径。第二阶段(H为150～400 mm)属于高冲击能量阶段，夹持区域内的颗粒完全破碎，破碎质量随着冲击高度缓慢增大。

落球高度的增加使冲击能量和冲击速度都增大，为区分两者对破碎质量的不同影响，开展了同一落球高度下不同冲击能量的落球实验(实验3)，实验通过在落球上方粘附不同质量块的方法改变冲击能量，其中，落球高度H=150 mm，钢球直径、颗粒粒径和料层厚度与实验2相同。实验3得到破碎质量随落球质量(冲击能量)的变化如图6所示。破碎质量在落球质量为200 g时略微偏大，其他的破碎质量基本相同，可见在冲击能量足够的情况下，料层破碎质量受冲击能量影响很小，冲击速度的增大会引起破碎质量的缓慢增加。

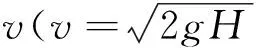
6.43 mm，并未随冲击高度(速度)的增大而线性增大，间接表明冲击速度的增大并不会引起夹持范围的增大。因此推断料层颗粒在被夹持前的滑移过程中发生了轻微破碎，冲击速度的增大加剧了该现象，使破碎质量出现细微增大。在计算料层破碎质量时，可考虑冲击速度的影响，并忽略其对夹持范围的影响。

3.3落球大小对夹持范围的影响

根据式(1)、式(2)与hn=2d 得到破碎质量与落球大小的关系：

m=πρ dD2sin2α/2

(4)

非限制料层静态夹持的角度α由料层颗粒特性决定[8]。对钢球直径在15～45mm的料层开展了冲击破碎实验(实验4)，其中，冲击高度、料层厚度和颗粒粒径与实验3相同。

实验4得到的破碎质量随落球直径变化的变化趋势(图7中离散点)与式(4)得到破碎质量变化趋势基本相似，因此忽略落球大小对夹持角度的影响，将实验结果用相应的抛物线拟合得到：

m=9.844×10-5D2

(5)

拟合的抛物线如图7中实线所示。

将粒度18～20目的石英砂参数ρ=1.43×10-3g/mm3，d=0.85mm代入式(4)，由式(4)与式(5)可得夹持角度α=14.26°，将其代入式(2)得该粒度下不同落球的夹持半径计算公式：

rn=Dsin14.26°/2

(6)

将D=25mm代入式(6)可得rn=6.16mm。在不同大小落球冲击下，未飞溅颗粒的破碎形态如图8所示，夹持区域的分布范围(直径)随着落球直径增大而线性增大，验证了上述的推论。图8所示的圆域直径远小于式(6)计算的夹持范围，是由于很大一部分颗粒破碎后飞溅到外围。

3.4颗粒粒度对夹持范围的影响

对颗粒粒径在0.24～1.09 mm的料层开展了冲击破碎实验(实验5)，其中，钢球直径、落球高度和料层厚度与实验3相同，不同颗粒粒径下的破碎质量如表1所示。

将表1的数据代入式(4)，得到不同粒度下的夹持角度，如图9所示。夹持角度受颗粒粒度的影响如下：粒径小于0.4 mm时，夹持角度变化不明显；粒径为0.4～0.85 mm时，夹持角度随着粒径增大而显著增大；粒径大于0.85 mm时，夹持角度范围略有减小。

不同粒度的非理想球形颗粒在形状和表面粗糙度上存在一定的差异[13]，这将导致料层夹持形态的差异。夹持料层层数为2时，最外沿颗粒O1的受力如图10所示。夹持角α≠0时，保证颗粒不滚动和不滑动的理论条件为

(7)

式中，F1、F2为颗粒所受正压力；Fs1、Fs2为颗粒与落球、颗粒间的摩擦力；μ1、μ2为颗粒与落球、颗粒间的摩擦因数；k为颗粒的滚动摩阻系数，与颗粒形状密切相关。

由式(7)可见，颗粒的形状和表面粗糙度对夹持角度存在显著的影响。通过分析石英砂颗粒图像可以发现，颗粒圆形度随着粒径的增大而减小，如图11所示。

被夹持的料层颗粒处于堆叠状态，颗粒间的接触点数量多，接触处的k、μ1、μ2难以直接测量，料层的夹持范围是众多接触力共同作用下平衡的结果。重力下颗粒自然堆叠的安息角能较好反映颗粒间的这种堆叠和接触状态。安息角的大小受颗粒形态的影响：通常颗粒球形度越高，表面越光滑，安息角越小[14]。通过固定圆锥法测得石英砂不同粒度下的安息角，如图12所示。

比较图12所示的安息角与图9所示的夹持角度可知，两者除了在粒度小于0.4 mm和大于0.85 mm有些差异外，整体的变化幅值和变化趋势基本相似，因此可用安息角来表示夹持角度：

α=ψ-θ

(8)

式中，θ为安息角和夹持角的平均差值，θ=23.61°。

将式(8)代入式(2)可得料层夹持半径：

rn=Dsin(ψ-23.61°)/2

(9)

结合式(4)，得到料层冲击破碎的质量：

m=πρ dD2sin2(ψ-23.61°)/2

(10)

选取在形状、表面粗糙度与石英砂略有差异的建筑砂，开展了落球冲击料层验证性实验。实验颗粒的破碎质量与式(10)的计算结果基本相符。

4结论

(1)通过不同厚度的非限制料层落球冲击破碎实验，确认了料层的夹持厚度为2层颗粒的堆叠厚度，简化了圆柱形夹持料层破碎质量的计算公式。

(2)不同高度和不同能量等级的落球实验表明，料层夹持范围受冲击能量的影响很小，落球的冲击速度对破碎质量略有影响。

(3)不同大小的落球实验表明，夹持范围随着落球直径的增大而增大，而落球大小对夹持角度影响很小，给出了石英砂落球直径与夹持半径计算公式。

(4)通过对不同粒度下的夹持角度、夹持颗粒受力和颗粒堆叠安息角的分析，建立了颗粒安息角与夹持角度的关系，给出了相应的料层夹持半径计算公式和料层冲击破碎质量的计算公式。

参考文献：

[1]陶珍东，郑少华. 粉体工程与设备[M]. 2版. 北京：化学工业出版社，2010.

[2]尹忠俊，张少军，李忠富. 振动磨筒体内部的能量传递规律[J]. 北京科技大学学报，2006，28(5)：471-474.

Yin Zhongjun，Zhang Shaojun，Li Zhongfu. Energy Transfer in a Vibrating Mill Tube[J]. Journal of University of Science and Technology Beijing，2006，28(5)：471-474.

[3]郑伟亮，盖国胜. 物料的不同粉碎方式和粉碎机理的研究[C]//2003年全国粉体设备-技术-产品信息交流会论文集. 上海，2003：127-134．

[4]Schönert K. The Influence of Particle Bed Configurations and Confinements on Particle Breakage[J]. International Journal of Mineral Processing，1996，44：1-16．[5]Tavares L M，Carvalho R M. Modeling Breakage Rates of Coarse Particles in Ball Mills[J]. Minerals Engineering，2009，22：650-659．[6]毛亚郎，孙毅，计时鸣，等. 介质球间非限制料层夹持形态研究[J]. 中国机械工程，2014，25(23):3212-3215．

MaoYalang, Sun Yi, Ji Shiming, et al. Nipped Configuration of Unconfined Particle Beds between Media Balls[J]. China Mechanical Engineering，2014，25(23)：3212-3215.

[7]Höfler A. Fundamental Breakage Studies of Mineral Particles with an Ultrafast Load Cell Device[D]．Salt Lake City：University of Utah，1990．

[8]Bourgeois F S. Single Particle Fracture as Basis for Microscale Modeling of Comminution Processes[D]. Salt Lake City：University of Utah，1993.

[9]Barrios G K P,Carvalho R M，Tavares L M. Modeling Breakage of Monodispersed Particles in Unconfined Beds[J]. Minerals Engineering，2011,24(3/4)：308-318.

[10]徐秉权. 料层粉碎研究的进展[J]. 湖南有色金属，1993，9(5)：278-281．

Xun Bingquan. Research Progress of Particle Beds[J]. Hunan Nonferrous Metals，1993，9(5)：278-281.

[11]Göll G，Hanisch J. 冲击应力和挤压应力对颗粒层的破碎效果的比较[J]. 岳守礼，译. 国外非金属矿，1988(4)：19-25．

[12]段希祥，曹亦俊. 球磨机介质工作理论与实践[M]. 北京：冶金工业出版社，1999．

[13]蒋阳，陶珍东. 粉体工程[M]. 武汉：武汉理工大学出版社，2008．

[14]谢洪勇，刘志军. 粉体力学与工程[M]. 2版. 北京：化学工业出版社，2007．

(编辑张洋)

Nipped Configuration of Unconfined Particle Beds under Falling Ball Impact Test

Mao YalangSun YiJi ShimingShan JihongJin Xiaohang

Zhejiang University of Technology，Hangzhou， 310014

Key words:falling ball impact; unconfined particle bed; nipped height；nipped range

Abstract:In order to establish the impact breakage model of unconfined particle beds and improve the grinding efficiencies in ball mill, a study of nipped configuration of unconfined particle beds was carried out on the basis of the falling ball impact test. The influence of bed height, impact energy, impact velocity, ball size, and particle size on nipped configuration were analyzed by the falling ball impact test. Experimental results show that on the conditions of sufficient impact energy, the bed height of the nipped particles is the stack height with 2 layers particles. The nipped range has a significant relationship with the falling ball size and the nipped angle. Finally, a mathematical model was built to analyze the relationship among nipped range radius, ball size and angle of repose.

收稿日期：2015-04-03

基金项目：国家自然科学基金资助项目(51275474，51505424)；浙江省自然科学基金资助项目(LZ12E05002，LY15E050019)

作者简介：毛亚郎，男，1978年生。浙江工业大学机械工程学院博士研究生。主要研究方向为粉磨机械与装备。发表论文3篇。孙毅，男，1966年生。浙江工业大学机械工程学院教授、博士研究生导师。计时鸣，男，1957年生。浙江工业大学机械工程学院教授、博士研究生导师。单继宏，男，1970年生。浙江工业大学机械工程学院副教授。金晓航，男，1981年生。浙江工业大学机械工程学院副教授。

中图分类号：TD921

DOI：10.3969/j.issn.1004-132X.2016.02.005