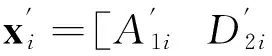一种基于几何特征的列车集尘器形状匹配算法

孙国栋　杨林杰　梅术正　赵大兴

湖北工业大学,武汉,430068



一种基于几何特征的列车集尘器形状匹配算法

孙国栋杨林杰梅术正赵大兴

湖北工业大学,武汉,430068

摘要：针对列车集尘器定位不准确的问题，提出了一种基于几何特征的形状匹配算法。该算法首先对轮廓点进行采样，基于极半径、局部曲率确定关键点的初始位置及点集的映射关系，然后以形心为基准，生成以角度和尺度为几何特征的双重描述子，并对其作标准量化处理。最后使用改进的曼哈顿距离计算描述子的相似性。实验结果表明,该形状匹配算法几乎不受伸缩、旋转、平移等几何变换的影响，具有一定的适应性和鲁棒性。

关键词：货车故障图像检测系统;集尘器;几何特征;形状匹配;描述子

0引言

货车故障图像检测系统(troubleofmovingfreightcardetectionsystem,TFDS)可有效克服人工列检的局限性，提高检测效率，对我国铁路货运事业的发展具有重要意义。轮廓作为一种高级别的视觉信息，其相关技术已被应用于多个领域，如目标识别、图像检索、医学图像分析、机器人导航等，但在TFDS中的应用相对较少，轮廓描述与匹配技术的研究一直是模式识别的热点问题[1-3]。最经典的是由Belongie等[4]提出的形状上下文(shapecontext,SC)描述方法,该方法主要描述轮廓序列上的某个点与其他所有点的空间分布关系,后续很多算法都对其作了改进，但实时性较差。孙晓鹏等[5]提出了一种基于耳廓点云形状特征匹配的路径跟随算法,该方法结合凸松弛方法与凹松弛方法,通过跟随凸凹问题的解路径，近似地求解图匹配问题。肖爱玲等[6]提出了一种基于标记的极半径极值红枣形状识别方法，主要通过边界追踪获取目标边界笛卡儿坐标，并将其转化为极坐标，从而完整地表达边界曲线。

本文研究的集尘器位于列车底部，主要用于从气体中收集悬浮粉尘与雾沫，防止粉尘进入制动管内，由于其存在较大的安装偏差，故难以通过一般的匹配算法定位所在区域。本文综合已有的研究成果，提出的集尘器形状匹配算法几乎不受伸缩、旋转、平移等几何变换的影响，具有较强的适应性。

1集尘器形状匹配流程

CCD相机采集到的列车集尘器如图1所示，矩形标记的部分为集尘器区域。集尘器形状匹配算法的总体流程如下：首先,通过预处理对采集图像进行轮廓提取，获得各部件的外轮廓并进行标记；然后,分别对各外轮廓进行关键点采样、确定每个轮廓的初始位置，以外轮廓形心为基准，生成以角度与尺度为几何特征的双重描述子，并对其作标准量化处理；之后，加载模板轮廓的描述子数据，使用改进的曼哈顿距离计算轮廓描述子间的相似性；最后确定集尘器所在区域。

2轮廓关键点

2.1轮廓关键点采样

由于轮廓邻近点之间的特征差异很小,所以没有必要计算每个轮廓点的特征。同时为了兼顾算法时间，采用沿轮廓链码方向对其进行均匀离散采样。本文约定初始点作为采样的起点,以逆时针为采样正方向,ls为采样步长,为处理简便和建立稳定的点集映射关系,设轮廓在任一几何变换下的采样点是一个常数N，本文取N=80，其值与轮廓的分辨率以及匹配精度有关。轮廓序列点集总数记为M，则ls的定义如下：

ls=M/N

(1)

按式(1)采样需注意一个问题：由于无法保证M正好是N的倍数,ls可能是一个属于[T,T+1)区间的小数且T∈N+。若以T作为步长会使部分轮廓无法参与采样，以T+1作为步长会产生点集越界，因此，单纯以T或T+1作为采样步长都是不合理的。于是，采取累加值求余的方式来计算采样步长，取其值的最邻近点为关键点，实验发现该采样方法更趋合理。集尘器外轮廓采样效果如图2所示，带圈的小点为关键点，与轮廓形心相连的点是采样的初始位置。可看出轮廓序列关键点并不是均匀分布的，而是随曲率大小而变化，轮廓变化明显处关键点相对更加密集。

2.2确定关键点初始位置

点集匹配通常采用动态规划算法，但其效率较低。因此,事先以同样的标准确定待匹配的采样点集的初始位置，选取关键点采样的顺序与方向，可避免点集匹配的动态搜索，显著提高形状匹配效率。但关键点初始位置的准确性直接影响了整个匹配的精度，因此，采用最大极半径与局部曲率约束来确定关键点初始位置。

首先计算标准轮廓的最大极半径及其对应点的局部曲率，分别记为ρsmax、ksmax。具体原理如下:设轮廓模型为L={vi|vi=(xi,yi),i=1,2,…,M},M为轮廓点集总数,其形心的坐标为O(x0,y0),计算公式为

(2)

轮廓最大极半径采用欧氏距离来度量,设其位置对应点为S(x,y),由下式可求出S的坐标：

(3)

`

i=1,2,…,N

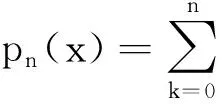
(4)

其中,ak为多元函数的系数,曲线拟合即可转化为求函数I=I(a0,a1,…,an)的极值问题,即

(5)

其对应的线性方程组用矩阵表示如下：

(6)

(7)

在列车集尘器形状匹配算法中,首先计算标准轮廓的ρsmax以及该点对应的ksmax,然后求取对应匹配轮廓的最大极半径,记为ρs,把极半径大于0.95ρs的点作为匹配轮廓初始位置的预选点,对预选点逐一遍历,计算其局部曲率km,若满足I=min(|km-ksmax||m=1,2,…,P),P为预选点的个数,km所对应的点S′(x′,y′)即匹配轮廓的初始点,该方法对于一般甚至复杂轮廓均能取得良好的实验效果。

3形状描述子

集尘器的形状轮廓线是由一系列具有特殊位置的点构成的,如何利用点集的空间信息形成稳定的描述子是其匹配算法的关键[7-8],本匹配算法以轮廓形心为基准，生成以角度与尺度为几何特征的双重描述子。

3.1角度描述子

对于轮廓上的任意一点，梯度向量并不是指向一个参考点，但梯度约束了轮廓可能的发展和走向，且其描述特征能够表达轮廓变化的重要信息。实验研究发现，以梯度为辅助基准，轮廓任意一点与形心的向量生成的角度描述子对轮廓具有稳定的描述特性，其生成原理如图3所示。

对于图3的轮廓模型任意一点ei(xi,yi),其对应的切向量和梯度向量分别为τi、fi，可知τi×fi=0,ei与形心生成的向量记为ri,角度描述子是以向量ri与fi的夹角作为描述特征的,其值可以通过向量的内积公式计算得到，即

θi=arccos

(8)

如图3所示,角度描述子的计算使用的不是绝对坐标，而是以向量ri为基准的相对坐标,其结果是一个具有完全旋转不变性的描述子。可以证明无论目标轮廓如何平移、旋转或缩放，梯度向量fi与向量ri的几何关系并没有发生变化,因此它们之间的夹角也始终保持不变。fi与τi的单位向量直线对应的斜率互为负倒数,又由式(8)可知fi与θi相关,则若切线τi存在偏差,θi定会存在等价的转动偏差,因此τi的求取也是一个重要的步骤,其结果直接影响着角度描述子的准确度。以上分析同时也表明θi更加侧重于描述轮廓切线方向的变化特征。

3.2尺度描述子

考虑到集尘器角度描述子更多描述的是其切向的发展趋势,不足以描述轮廓完整的变化信息,因此有必要附加一个纵向的尺度描述子。基于边界的极半径可以很好地表示集尘器轮廓在纵向的变化信息,随着边界点的移动，轮廓点与形心之间的距离(极半径)变化曲线是一个轮廓所特有的。设任意一点ei(xi,yi)对应的极半径记为Ri，从图3看出Ri=|ri|,由于ri使用的也是基于形心生成的相对坐标,所以其模值不受轮廓平移、旋转的影响。考虑到列车车体振动会引起物距的变化，造成集尘器轮廓的尺度变换，为保证尺度描述子的尺度不变性，对Ri作归一处理，以极半径的最大值作为归一化的基准，设最大距离为Rmax,归一化后的值为Di,尺度描述子的定义为

Di=Ri/RmaxDi∈(0,1]

(9)

通过上述方法建立了以形心为辅助基准的角度与尺度特征描述子，分别生成1×N的特征向量，记为A=(θ1,θ2,…,θN)和C=(D1,D2,…,DN)。图4～图8分别给出了集尘器部分外轮廓在几何变换下的采样效果图及对应的描述子曲线分布图，从图5～图8可以看出，角度与尺度描述子在集尘器几何变换下的各拟合曲线十分接近，表明该描述子具有较强的鲁棒性。

4集尘器形状描述子相似性度量算法

针对生成的集尘器角度和尺度描述子的量纲不同问题，采用了基于期望与方差的量化方法，并把曼哈顿距离作为匹配形状描述子之间的相似性度量方式。

4.1描述子标准化

参考形状和待匹配形状轮廓描述子分别记为

q*=(q-m)/s

(10)

其中,q为量化的输入值,m为量化类型均值,s为标准差,q*为标准量化后的值,分别将描述子X与X′中的分量代入式(10),则轮廓标准量化后对应值X*与X′*分别为

(11)

4.2描述子的相似性度量

描述子的相似性度量也是列车集尘器形状匹配的一个重要步骤，度量算法的优劣直接影响着匹配的准确度[9-10]。通过多种距离实验效果比对同时兼顾算法时间，发现曼哈顿距离更适合度量集尘器生成的形状描述子，从图5～图8可以看出使用向量式坐标轴投影的曼哈顿距离可有效抵制描述子曲线波形微小相位偏移引起的匹配误差，尤其对多维且独立的分量有比较好的度量效果。特征描述子X*与X′*度量公式为

(12)

其中,Rmat为匹配值,其值越小表明轮廓的相似度越高。

5实验分析与结论

为了验证算法的有效性，依次对检测目标图像进行伸缩、旋转、平移变换，计算轮廓之间的相似度，匹配值的结果见表1。其中,Ds、Rs分别表示尺度和角度几何变换系数,Av、Dv分别表示在单一角度描述子与尺度描述子的匹配值,各匹配值保留4位小数,其表达式为

从表1可看出,本文提出的列车集尘器形状匹配算法基本上不受几何变换的影响，匹配值的偏差也在很小的数量级内，标准量化后描述子的匹配值相比单一描述子显示出了更大的优越性，集尘器形状在尺度、旋转变换下的单一角度描述子匹配值Av与尺度描述子匹配值Dv的数量级在10-1至10-3内,而量化后的描述子的匹配值Rmat的数量级在10-3至10-5之间,因此该描述子受几何变换的影响很小。

同时可看出量化后的描述子在尺度变换下的匹配值比旋转变换低一个数量级，表明匹配值Rmat对旋转变换略敏感一点,主要是因为旋转会引起集尘器轮廓序列点微小变化,从而使点集间的映射关系发生细微偏移,因此偏差略大一些。

为了验证算法的效率和适应性,对样本以外具有不同几何变换的集尘器图像进行测试，实验运行时间t(不包括图像预处理[11])和匹配值Rmat见表2。

从表2可以看出,匹配值并没有受样本外采集图像的影响，说明匹配算法具有一定的适应性,匹配算法时间均值为0.4979ms，完全能够满足实时性检测要求。

综上，本算法仍然可在设置低阈值情况下，得到精确的匹配效果。实验环境为Xeon3.40GHz,内存8GB的PC机,操作系统为Windows7 32位,编程软件为VisualStudio2010+OpenCV2.4.4。

实验结果表明集尘器形状匹配方法几乎不受伸缩、旋转、平移等几何变换的影响，相对其他常见的匹配算法具有一定的优势，为TFDS故障识别提供了一种全新的思路。今后主要将使用动态规划算法对轮廓间的关键点集映射关系进行研究，进一步改进相似性度量方法。

参考文献:

[1]周瑜, 刘俊涛,白翔.形状匹配方法研究与展望[J].自动化学报, 2012, 38(6): 890-910.

ZhouYu,LiuJuntao,BaiXiang.ResearchandPerspectiveonShapeMatching[J].ActaAutomaticaSinica,2012, 38(6):879-910.

[2]孙国栋, 徐威, 梁永强, 等. 基于形状上下文的列车挡键丢失图像识别算法[J].铁道科学与工程学报, 2014, 11(6): 127-131.

SunGuodong,XuWei,LiangYongqiang,etal.ImageRecognitionAlgorithmforSideFrameKeyofTrainBasedonShapeContext[J].JournalofRailwayScienceandEngineering, 2014, 11(6):127-131.

[3]王英, 陈建能, 赵雄, 等. 基于NURBS曲线的凸轮廓线表达方法的研究及应用[J].中国机械工程，2013,24(10)：1375-1379.

WangYing,ChenJianneng,ZhaoXiong,etal.StudyonCamProfile’sExpressionMethodandItsApplicationsBasedonNURBSCurves[J].ChinaMechanicalEngineering, 2013 ,24(10)：1375-1379.

[4]BelongieS,MalikJ,PuzichaJ.ShapeMatchingandObjectRecognitionUsingShapeContexts[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2002, 24(4): 509-522.

[5]孙晓鹏, 李思慧, 王璐. 耳廓点云形状特征匹配的路径跟随算法[J].软件学报, 2015, 26(5): 1251-1264.SunXiaopeng,LiSihui,WangLu.ShapeFeatureMatchingAlgorithmofEarPointCloudUsingPathFollowing[J].JournalofSoftware, 2015, 26(5):1251-1264.

[6]肖爱玲, 潘斌. 基于标记的极半径极值红枣形状识别方法[J].农机化研究, 2015(7):61-65.

XiaoAiling，PanBin.IdentificationoftheShapeofChineseDateBasedonLabellingMethodandExtremumofPolarRadius[J].JournalofAgriculturalMechanizationResearch, 2015(7): 61-65.

[7]StegerC,UirichM,WeedemannC.MachineVisionAlgorithmsandApplication[M].Beijing:TsinghuaUniversityPress, 2008.

[8]王斌.一种不变的基于傅里叶变换的区域形状描述子[J].电子学报, 2012, 40(1): 84-88.

WangBin.AnInvariantRegion-shapeDescriptorBasedonFourierTransform[J].ActaElectronicaSinica, 2012, 40(1): 84-88.

[9]崔峰, 汪雪林, 彭思龙.近似欧氏距离变换的一种并行算法[J].中国图象图形学报,2004,9(6):693-698.

CuiFeng,WangXuelin,PengSilong.AParallelAlgorithmforQuasiEuclideanDistanceTransform[J].JournalofImageandGraphics, 2004, 9(6): 693-698.

[10]徐少平, 张华, 江顺亮, 等. 基于直觉模糊集的图像相似性度量[J].模式识别与人工智能,2009,22(1):156-161.

XuShaoping,ZhangHua,JiangShunliang,etal.ImageSimilarityMeasureBasedonIntuitionisticFuzzySet[J].PatternRecognitionandArtificialIntelligence, 2009, 22(1): 156-161.

[11]赵大兴, 王璜, 朱锦雷, 等.高精度自适应阈值分割算子的设计[J].计算机应用, 2008, 28(7): 1742-1743.

ZhaoDaxing,WangHuang,ZhuJinlei,etal.DesignofThresholdingSegmentationOperatorwithHighPrecisionSelf-adaptiveCapacity[J].ComputerApplications, 2008, 28(7):1742-1743.

(编辑陈勇)

AShapeMatchingMethodforTrainDustCollectorBasedonGeometricalFeatures

SunGuodongYangLinjieMeiShuzhengZhaoDaxing

HubeiUniversityofTechnology,Wuhan,430068

Keywords:troubleofmovingfreightcardetectionsystem(TFDS);dustcollector;geometricfeature;shapematching;descriptor

Abstract:Duetotheproblemofinaccuratepositioningofthetraindustcollector,ashapematchingmethodwasproposedbasedongeometricfeatures.Firstly,thecontourpointsweresampledandinitiallocationofcriticalpointsandmappingrelationsofpointsetsweredeterminedbasedonpolarradiusandlocalcurvature.Thentakingcentroidasabenchmark,dualdescriptorswithgeometricfeaturesofanglesandscalesweregeneratedandprocessedbystandardquantification.Finally,thesimilarityofthedescriptorswascalculatedwithmodifiedManhattandistance.Theexperimentalresultsshowthattheproposedshapematchingmethodisharldyinfluencedbygeometrictransformationsuchasscale,rotation,andtranslation,whichdemonstratesitsadaptabilityandrobust.

收稿日期：2015-09-09

基金项目:国家自然科学基金资助项目(51205115)

作者简介：孙国栋,男,1981年生。湖北工业大学机械工程学院副教授、博士。主要研究方向为产品质量视觉检测与机器学习等。杨林杰,男,1990年生。湖北工业大学机械工程学院硕士研究生。梅术正,男,1991年生。湖北工业大学机械工程学院硕士研究生。赵大兴,男，1962年生。湖北工业大学机械工程学院教授、博士。

中图分类号：TP29

DOI：10.3969/j.issn.1004-132X.2016.02.014