基于时间常数外圆切入磨削砂轮钝化的监测方法

迟玉伦　李郝林

上海理工大学，上海，200093



基于时间常数外圆切入磨削砂轮钝化的监测方法

迟玉伦李郝林

上海理工大学，上海，200093

摘要：基于外圆切入磨削力模型研究，提出了一种在线监测功率信号的时间常数算法，并利用时间常数对外圆切入磨削砂轮钝化状态进行识别。为提高计算准确性，选取了进给阶段稳定功率信号和驻留阶段功率信号变化率对时间常数进行计算。通过不同磨削工艺参数和不同修整工艺参数实验，验证了利用功率信号的时间常数方法对砂轮钝化监测的有效性。

关键词：砂轮钝化；功率信号；时间常数；实验

0引言

在精密磨削加工中，砂轮的钝化状态是砂轮磨削性能的重要指标之一，它直接影响着磨削加工的生产效率和加工质量[1]。砂轮钝化后，磨粒逐渐失去切削能力，若继续磨削则可能会产生磨削烧伤和磨削颤振等现象。在实际磨削加工过程中，为了避免砂轮钝化影响加工表面质量，大都采用定时修整策略，即在砂轮尚未达到工作寿命极限时，提前对其进行修整[2-3]。频繁修整砂轮不仅会降低加工效率，也会加快砂轮的损耗，特别是一些价格昂贵砂轮的损耗，会严重增加企业的经济负担[4]。因此，如何有效地在线监测砂轮的钝化状态，根据实际砂轮钝化情况确定修整时间，对提高磨削效率和磨削表面质量有着重要意义。

近年来国内外学者对砂轮钝化监测进行了大量研究。孔亚东等[5]利用多传感器信息融合技术，通过模糊分类的方法对不同的磨削条件进行模糊化处理，构建了砂轮钝化监测多传感器融合系统结构，实验结果证明它比使用单一传感器方法识别率高，监测效果更好；王强等[6]提出了基于声发射信号归原处理法及能量系数法相结合的砂轮磨损状态检测方法，实验结果表明该检测方法能够有效地判断砂轮磨损的状态；李德广等[7]通过对磨削力进行谐波小波包分解，得到无频谱混叠的磨削力的时频分布图，分析了通过时频分布图提取砂轮状态特征的可行性；Sutowski等[8]基于声发射均方根(RMS)信号提出了一种新的能量系数对砂轮钝化进行监测，实验验证了该方法的有效性；Liao等[9-10]利用小波包对声发射信号进行提取，根据砂轮锋利和钝化时的特征参数，利用自适应遗传聚类算法对砂轮不同钝化状态进行识别，在不同磨削去除率条件下该方法聚类精度达到76.7%以上；Yang等[11]提出了基于声发射信号的小波包和支持向量机方法对磨削砂轮钝化进行识别，通过不同磨削实验验证该方法的分类精度达到99.39%以上。上述研究虽能对砂轮钝化状态给予准确判别，但其模型过于复杂且对实验条件有较高要求，很难应用于实际加工过程。

本文基于外圆切入磨削力模型研究，提出了一种在线监测功率信号的时间常数算法，并根据时间常数对外圆切入磨削砂轮钝化状态进行识别。为提高计算准确性，本文选取了进给阶段稳定功率信号和驻留阶段功率信号变化率对时间常数进行计算。通过不同磨削工艺参数和不同修整工艺参数实验，验证了利用功率信号的时间常数方法对砂轮钝化监测的有效性，该方法为选取磨削工艺参数和修整工艺参数提供了参考依据，对提高磨削工件表面质量和磨削效率有重要意义。

1外圆切入磨削力模型与时间常数

磨削过程中产生的切削力使机床、砂轮和工件发生了弹性变形和较大的位移。如图1所示，外圆切入磨削力模型可以简化成三个弹簧系统，分别为砂轮刚度ks，工件刚度kw，砂轮与工件接触刚度ka。

图1所示系统的等效刚度ke可表示为

(1)

外圆切入磨削进给过程中，砂轮工件接触点的法向磨削力Fn产生的弹性变形δ可表示为

(2)

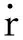
(3)

(4)

砂轮的径向磨损可以用磨削比G来表示。磨削比是指被切除的切屑体积与砂轮损耗体积之比。对于外圆切入磨削，有

(5)

(6)

式中，b为砂轮厚度;ds为砂轮直径；dw为工件直径。

联立式(1)、式(3)、式(4)和式(6)可得磨削系统控制公式[14]：

(7)

经变换整理得

(8)

其中，τ为磨削系统时间常数，可表示为

(9)

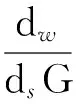
(10)

(11)

对上述常系数非齐次微分方程进行求解，可获得外圆切入磨削进给阶段和驻留阶段的磨削去除率公式[15]：

(12)

式中，t1为进给时间。

时间常数τ与系统等效刚度ke、磨削力系数kc及工件转速nw有关。由式(1)可知，等效刚度ke由砂轮刚度ks、工件刚度kw、砂轮与工件接触刚度ka组成。假设磨削加工时砂轮刚度ks与工件刚度kw不变，当磨削砂轮逐渐钝化时，磨削力系数kc会逐渐增大，时间常数τ随着磨削砂轮钝化而增大[16]。因此，本文利用功率信号的时间常数τ的变化对砂轮钝化进行监测研究。

2基于功率信号的时间常数计算方法

根据外圆切入磨削原理，磨削过程中砂轮和工件都在转动，传统的磨削力传感器无法安装到有效位置来直接测量切入磨削力。磨削功率信号对砂轮磨削切向力变化非常灵敏，有很好的线性关系，故本文利用功率信号计算时间常数τ。

(13)

式中，vs为砂轮线速度。

则砂轮磨削主轴的功率为

P=kPFtvs

(14)

式中，kP为功率系数，其大小取决于磨削条件；Ft为切向磨削力。

切入磨削过程中，法向磨削力Fn与切向磨削力Ft的关系为

Fn=kntFt

(15)

式中，knt为法向磨削力与切向磨削力的比例系数。

联立式(3)、式(12)、式(14)和式(15)得外圆切入磨削的功率信号理论模型为

(16)

(17)

(18)

式中，Ks为常数系数。

根据式(17)和式(18)，通过稳定阶段的功率信号和功率信号变化率可计算出时间常数τ，即

(19)

3实验研究

本文基于功率信号对砂轮切入磨削过程进行监测,采用实验验证式(19)对砂轮钝化过程监测的有效性。

3.1实验设置

如图2所示，实验机床为德国斯莱福临公司STUDERK-C33精密外圆磨床，机床主轴转速为1～1500r/min，最小进给量为0.1μm；砂轮型号为53A80L15V，厚度b为62mm，直径ds为440mm；工件材料为45钢，直径dw为50mm。磨削时砂轮线速度为35m/s，工件转速为120r/min。磨削冷却液为嘉实多HysolR水基磨削液。

本文利用功率传感器在线监测外圆切入磨削加工过程。功率传感器安装在机床电器柜中，在线测量磨削加工砂轮主轴电机功率变化，采用LOADCONTROL公司的PH-3型功率传感器，响应时间为0.015s，量程为50kW；本文记录功率信号的数据采集卡型号为SpectrumM1.3120(2通道，12位A/D转换)，采集软件使用DEWESoft。

本实验是利用功率信号在线监测砂轮钝化过程，为验证上述理论方法的有效性，本文使用3D显微镜在机检测砂轮表面磨损情况，如图3所示，砂轮切入磨削结束后，将3D显微镜安装在台面上对砂轮表面进行分析验证。

对表1和表2所示的6组参数，分别进行多次重复进给磨削直至砂轮钝化，同时记录功率信号，对砂轮钝化过程进行分析。

3.2结果讨论

如图4所示，一个外圆切入磨削加工循环过程的功率信号分为进给阶段和驻留阶段。进给阶段的功率信号由于磨削弹性变形从开始逐渐增大直到稳定阶段，进入驻留阶段后功率信号逐渐减小，磨削弹性变形逐渐恢复。

本文利用磨削功率信号P在进给阶段的稳定功率信号P′计算常数系数Ks，如图4所示。

为了验证上述方法的有效性，利用计算后的常数系数Ks和时间常数τ对磨削功率进行预测，如图5所示，可看出，预测的功率信号和测量的功率信号非常接近，证明利用最小二乘法计算时间常数τ是比较准确的。

3.2.1修整工艺参数不变，改变磨削工艺参数

对表1所示的第1组工艺参数进行多次重复切入式磨削直至砂轮完全钝化。基于上述利用功率信号计算时间常数的方法，对每一次切入磨削循环驻留阶段的时间常数进行计算，并整理时间常数随磨削次数的变化曲线，如图6所示。

由图6可以看出，砂轮整个钝化过程可分为三个阶段，即自锐阶段、逐渐磨损阶段和完全钝化阶段。当砂轮开始磨削时，由于新修整后的砂轮并不是锋利的，所以需要一个自锐过程，该过程磨削力逐渐减小，因此自锐阶段功率信号时间常数值变小。当砂轮继续磨削时，砂轮开始逐渐磨损钝化，磨削力逐渐增大，时间常数值随着砂轮逐渐磨损而变大，如图6中第2至第7次磨削循环曲线所示。当砂轮完全钝化后，磨削发生颤振，磨削力也非常不稳定，所以时间常数也不再继续增大而是不规则变化，如图6中第8次磨削循环后曲线所示。

为了验证上述时间常数监测方法的有效性，本实验利用3D显微镜分别对自锐阶段、逐渐磨损阶段和完全钝化阶段的砂轮表面特征进行分析，图7为砂轮表面3D显微镜图。由图7a可知，砂轮自锐阶段的磨粒较为锋利，对应图6中自锐阶段时间常数；由图7b和图7c可知，砂轮逐渐磨损阶段磨粒逐渐磨损且残留在砂轮表面上的切屑也逐渐增多，对应图6中逐渐磨损阶段时间常数；由图7d可知，砂轮完全钝化阶段的砂轮磨粒已经严重磨损且砂轮堵塞较为严重，对应图6中完全钝化阶段时间常数。

图6所示的基于时间常数对砂轮钝化监测分析结果与图7所示利用3D显微镜观测的砂轮磨损过程一致，证明了本文利用功率信号时间常数监测砂轮钝化过程的有效性。

利用类似实验方法，分别对表1中第2组和第3组工艺参数进行实验，并计算其时间常数随磨削次数的变化，如图8和图9所示。

3.2.2磨削工艺参数不变，改变修整工艺参数

利用表2中一组修整工艺参数对砂轮进行修整，修整后的砂轮进行多次重复切入式磨削直至砂轮完全钝化。

分别完成表2中3组修整参数的砂轮钝化磨削实验，利用上述方法同样计算其时间常数变化，结果如图10～图12所示。可以看出，随着砂轮修整深度的增大，时间常数逐渐减小，砂轮达到完全钝化的磨削次数逐渐增加。砂轮修整深度越大，砂轮表面形成的有效磨粒数越多，砂轮越锋利，即时间常数逐渐减小；修整深度较大的砂轮在磨削加工过程中不容易钝化，所以，砂轮达到完全钝化的磨削次数随着修整深度增大逐渐增加。

通过上述不同磨削工艺参数和不同修整工艺参数的实验研究，验证了利用功率信号的时间常数方法对砂轮钝化监测的有效性。实验结果也为如何选取磨削工艺参数和修整工艺参数提供了参考依据，对后续提高磨削工件表面质量和磨削效率有重要意义。

4结论

(1)基于外圆切入磨削力模型分析，研究了功率信号的时间常数与砂轮钝化的关系，提出了利用功率信号的时间常数对磨削砂轮钝化过程进行监测的方法。

(2)建立了磨削功率信号与磨削力关系模型，通过在线监测外圆切入磨削的功率信号对时间常数进行识别。为了提高计算准确性，本文选取了进给阶段稳定功率信号和驻留阶段的功率信号变化率对时间常数进行计算。

(3)利用3D显微镜分别对自锐阶段、逐渐磨损阶段和完全钝化阶段的砂轮表面特征进行分析，并与基于时间常数对砂轮钝化的监测结果进行对比，证明了上述利用功率信号时间常数监测砂轮钝化过程的有效性。

参考文献：

[1]WegenerK,HoffmeisterHW,KarpuschewskiB,etal.ConditioningandMonitoringofGrindingWheels[J].CIRPAnnals-ManufacturingTechnology,2011,60:757-777.

[2]刘贵杰,唐婷,刘立静,等.基于声发射信号的砂轮钝化在线检测方法[J].仪器仪表学报,2005, 26(8):13-14.

LiuGuijie,TangTing,LiuLijing,etal.AcousticEmissionSignalsBasedOn-lineMonitoringMethodforWheelDull[J].ChineseJournalofScientificInstrument, 2005, 26(8):13-14.

[3]KarpuschewskiB,WehmeierM,InasakiI.GrindingMonitoringSystemBasedonPowerandAcousticEmissionSensors[J].AnnalsoftheCIRP, 2000, 49(1):235-240.

[4]KwakJae-Seob,HaMan-Kyung.NeuralNetworkApproachforDiagnosisofGrindingOperationbyAcousticEmissionandPowerSignals[J].JournalofMaterialsProcessingTechnology,2004, 147:65-71.[5]孔亚东,吕洋,王宛山,等.基于多传感器融合的磨削砂轮钝化的智能监测[J].东北大学学报(自然科学版),2003,24(3):248-251.

KongYadong,LüYang,WangWanshan,etal.IntelligentMonitoringforGrindingWheelPassivationBasedonMulti-sensorFusion[J].JournalofNortheasternUniversity, 2003, 24(3):248-251.

[6]王强,刘贵杰,王宛山.基于小波包能量系数法的砂轮状态监测[J].中国机械工程,2009, 20(3): 285-287.

WangQiang,LiuGuijie,WangWanshan.MonitoringMethodforGrindingWheelBasedonCapacityCoefficientoftheWaveletPackets[J].ChinaMechanicalEngineering,2009,20(3): 285-287.

[7]李德广,刘淑琴.基于谐波小波的磨削砂轮状态特征提取[J].振动、测试与诊断,2012,32(5): 750-755.LiDeguang,LiuShuqin.WheelStateFeatureExtractionBasedonHarmonicWaveletAnalysis[J].JournalofVibrationMeasurement&Diagnosis, 2012, 32(5): 750-755.[8]SutowskiP,PlichtaS.AnInvestigationoftheGrindingWheelWearwiththeUseofRoot-mean-squareValueofAcousticEmission[J].ArchivesofCivilandMechanicalEngineering,2006, 6(1):87-98.[9]LiaoTW,TingCF,QuJ,etal.AWavelet-basedMethodologyforGrindingWheelConditionMonitoring[J]InternationalJournalofMachineTools&Manufacture， 2007，47:580-592.

[10]LiaoTW.FeatureExtractionandSelectionfromAcousticEmissionSignalswithanApplicationinGrindingWheelConditionMonitoring[J].EngineeringApplicationsofArtificialIntelligence,2010，23:74-84.

[11]YangZhensheng,YuZhonghua.GrindingWheelWearMonitoringBasedonWaveletAnalysisandSupportVectorMachine[J].Int.J.Adv.Manuf.Technol.,2012,62:107-121.

[12]MarshER,MoerleinAW,DeakyneTRS,etal.In-processMeasurementofFormErrorandForceinCylindrical-plungeGrinding[J].Precis.Eng., 2008,32:348-352.

[13]马尔金S.磨削技术与理论[M].蔡光起，巩亚东，宋贵亮,译.沈阳：东北大学出版社，2002.

[14]ChenX,RoweWB,MillsB,etal.AnalysisandSimulationoftheGrindingProcess.PartⅢ.ComparisonwithExperiment[J].InternationalJournalofMachineToolsandManufacture, 1996, 36(8):897-906.

[15]HeckerRL,LiangSY,XiaoJianwu,etal.GrindingForceandPowerModelingBasedonChipThicknessAnlaysis[J].Int.J.Adv.Manuf.Technol.,2007,33:449-459.

[16]AlexWM,ErcRM,TheodoreRS,etal.In-processForceMeasurementforDiameterControlinPrecisionCylindricalGrinding[J].Int.J.Adv.Manuf.Technl.,2009, 42:93-101.

(编辑苏卫国)

MonitoringMethodofCylindricalPlungeGrindingWheelWearBasedonTimeConstant

ChiYulunLiHaolin

UniversityofShanghaiforScienceandTechnology,Shanghai,200093

Keywords:grindingwheelwear;powersignal;timeconstant;experiment

Abstract:Basedoncylindricalplungegrindingforcemodel,anewalgorithmoftimeconstantwasproposedbyusingpowersignals,andthetimeconstantwasusedtoidentifygrindingwheelwearstatus.Inordertoimprovecalculationaccuracy,grindingpowersignalsintheinfeedstageanddwellstagewereselectedtocalculatethetimeconstant.Atlast,throughexperimentsofdifferentgrindingprocessparametersanddifferentdressingparameters,thevalidityofmonitoringmethodwasproved.

收稿日期：2015-04-28

基金项目：国家科技重大专项(2013ZX04008-011)

作者简介：迟玉伦，男，1982年生。上海理工大学机械工程学院博士研究生。研究方向为精密测量技术。李郝林，男，1961年生。上海理工大学机械工程学院教授。

中图分类号：TG581.1

DOI：10.3969/j.issn.1004-132X.2016.02.011