课例：认识三角形

代德容

一、教学设计

课题：认识三角形

教学目标：

知识与技能：

1.了解三角形的基本元素与主要线段.，边角对应关系。

2.能区分不同形状的三角形，按角、按边分类的两种方法.

3.理解等腰三角形、等边三角形的概念.

过程与方法：联系已学过的有关知识，经历探索三角形基本知识的过程，通过几何画板从动态的角度研究问题。

情感态度：结合实践与应用，充分感受三角形的有关概念，体会三角形按角、按边的分类方法.，体会分类讨论的思想。

教学重点：三角形内角、外角，等腰三角形、等边三角形等概念.

教学难点：三角形的外角

教学过程：

（一）创设情境

问题与情境：播放PPT，展示各种生活中铺设的瓷砖

教师活动：利用多媒体展示问题

学生活动：观察从中找到数学问题

设计意图：从学生的实际生活出发，创设情境，激发学生的求知欲望。

（二）探究新知

问题与情境：利用几何画板学习以下知识：

1、三角形的相关概念：定义，顶点，边，内角，外角，对角，对边

2、三角形的分类：按角、按边

教师活动：应用几何画板展示三角形的相关概念，并对某些知识进行引导讲解。

学生活动：首先阅读教材，自主学习，然后在教师的点拨下，结合几何画板的动态演示解决预习中存在的问题，学生动手画三角形的外角，形成概念，最后互助学习，以優带差，督促后进生的学习。

设计意图：三角形是本章多边形学习的基础，掌握了它的有关概念，以后就可以用类比的方法学习其它多边形的相关内容。采用几何画板来演示，动态的画面更能吸引学生的兴趣，让学生数形结合，符合学生的认知水平，全面观察动态变化，有利于学生归纳，形成概念。初步体会分类讨论的思想。

3、例题解析

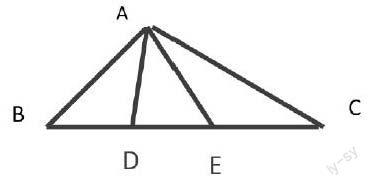
例、图中以BC为边的三角形共有_____个；它们分别_________.在△ABD中，∠A是_____边的对角，∠ADB是△_____的内角，又是_____的一个外角。

教师活动：多媒体展示，抽学生回答，根据学生回答的结果，在图形上再描述，辅助其他学生理解，便于其他学生发现问题。

学生活动：个别学生起立回答问题，其余学生在教师的语言动作的引导下完成本部分学案

设计意图：学生学习知识的目的是最终形成能力。而巩固、消化一个新的数学概念、数学基础知识，需要消化一些典型的例题，最终才能掌握这些知识概念。同时例题可以把知识、学习技能、思想方法综合在一起。例题是把具体知识点转化为学习能力的桥梁。

（三）课堂精练

1、基础过关

请同学们任画一个三角形，标记它的名字，回答以下问题：

（1）说出三角形的顶点、三条边、三内角的名字。

（2）画出它的一个外角，并标记名字。

（3）分别从边、角的分类说出此三角形的形状，为什么？

2、拓展提升

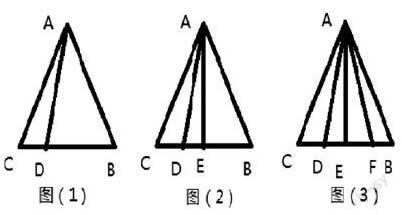
（1）在⊿ABC中，有一条线段AD时，如图（1）所示，图中有——个三角形；

（2）在⊿ABC中，有两条线段AD、AE时，如图（2）所示，图中有———个三角形；

（3）在⊿ABC中，有三条线段AD、AE、AF时，如图（3）所示，图中有———个三角形；

（4）在⊿ABC中，有n条线段时，猜想图形中有————个三角形，由此得出，在⊿ABC中，有2015条线段时，图形中有————个三角形。

教师活动：多媒体展示，对于学生不会的题目进行点拨、引导。

学生活动：先独学，在群学完成练习

设计意图：课堂练习是数学教学的重要组成部分，是使学生掌握知识、形成技能、发展智力的重要手段。这组练习分基础过关和拓展提升，实现了新课标的要求，“数学要面向全体学生，人人学有价值的数学，人人都获得必需的数学，不同的人在数学上得到不同的发展。”

（四）小结展示

师生活动：师生合作补充完成本节课的简单的思维导图

设计意图：使学生对本节课的学习内容有一个清晰的认识。为后续画思维导图打下基础。

（五）当堂检测

师生活动：1、如图所示的图中，以E为顶点的三角形有———个，分别是————；

在⊿ABC中，∠B的对边是———；在⊿ADE中，AD所对的角是_______

2、已知⊿ABC的一个外角为500，那么⊿ABC一定是（）

A、锐角三角形B、直角三角形

C、钝角三角形D、锐角三角形或钝角三角形

设计意图：在课堂教学中，教师并不能全面了解学生的学习情况，通过检测教师就能知道哪些同学完成了本节课的学习目标，哪些没有，便于之后教师进一步实施有效的教学措施。

二、本节课教学反思

（1）学习目标以及教学重难点把握准确、恰当，符合课标要求和学生认知水

（2）教学过程环环相扣，循序渐进，每个内容的设计合理，①.充分体现学生是学习活动的主体，教师是学习活动的引导者。②.体现了新课标的要求，“数学要面向全体学生，人人学有价值的数学，人人都获得必需的数学，不同的人在数学上得到不同的发展。”本环节尊重学生的个体差异，题目由易到难，一步步引导学生将问题深化，揭示解题规律，发展思维能力，使不同的学生各自都有收获。

（3）本节课采用了在PPT中插入几何画板演示学习内容，使教学的表现内容与形式更加形象化、生动化、多样化、趣味化，使数与形完美结合，有利于学生建构数学知识，培养了学生数形结合的数学。