数字系统中的几种编码定义问题讨论

丘洪伟

（广州工商学院 计算机科学与工程系，广州 510850）

数字系统中的几种编码定义问题讨论

丘洪伟

（广州工商学院 计算机科学与工程系，广州 510850）

本文讨论数字系统特别是计算机中几种二进制和十进制机器码即原码、反码、补码和移码的定义及其定义域问题；给出它们的精确定义，并通过实例加以说明.

真值；原码；反码；补码和移码；定义和定义域问题；精确定义

1 引言

通常，人们用正负符号加上一组数字的集合来表征一个数.在计算机中,数的“+”、“-”符号常用 0和 1表示；这种符号数字化后按一定规则产生的数称为机器数.机器数代表的实际值称为真值.把真值转换为机器数的方法就是所谓的编码方法.原码、反码、补码和移码就是机器数的基本编码形式.

对机器数的求取，文献［1］用列表和举例的方式给予了说明；对机器数编码的定义，文献［2—6］进行了很好的论述.本文则对每种编码的求取给出了精确的定义和定义域；在定义域中,用+0和-0表示 0的两种编码形式；补码和移码的定义，分别采用三段和二段函数来解决定义域内最小负值即端点之值的求取问题.

现考察一个 n位二进制数 x（含 1位符号位）的相关定义：

整数补码定义

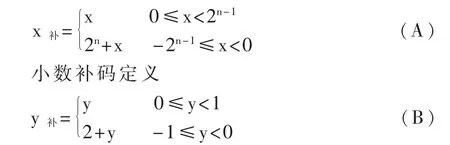
上述定义中，(A)式未界定整数补码的最大正值2n-1-1；而按定义求得的最小负值应为-2n-1+ 1，并非-2n-1；就是说用(A)式的第二段定义是无法求得最小负值-2n-1的.(B)式则未界定小数补码的最大正值 1-2-(n-1).对于其它编码的定义也有类似情形，不再赘述.

用定义求取机器数是学习和掌握各类编码的基础.因此定义应该是严谨的,根据定义求出的结果应该是唯一的,否则就会产生错误,误导读者.上述问题，恐怕是没有引起人们的重视或疏漏之故所致.致使许多学者根据给定的真值求取定义域端点处的某种编码值时，经常患难或失误.这就是为什么要讨论这一问题的原因.

2 原码、反码、补码和移码的精确定义

在实际中,所给定的整数或小数真值的数位长度(包括符号位)都是确定的.人们通常根据真值的长度求取相关机器数的编码，显然已假定机器的字长与真值的字长是相同的.只有当求值的结果超出真值的长度时,才考虑对结果的“最高位”进行处理的问题.因此，机器数在其定义域的端点之值是完全确定的.为使讨论问题方便，现设定真值的形式如下：

x=x0x1x2…xn是一个包括 1位符号位的 n+1位整数真值（注意：x0是符号位）；

y=y0.y1y2…yn是一个包括 1位符号位的 n+1位小数真值（注意：y0是符号位）.

当设定式的长度标注方式不同时 （如 n-1，n位），将导致定义及定义域的表达式各异.显然x和y的数值部分均为n位.对以上设定,以下不再说明.

据此可给出原码、反码、补码和移码的精确定义如下：

2.1 二进制数编码定义

定义1 整数原码

2.2 十进制数编码定义

定义 11 小数反码(“9的补数”)

3 说明和示例

例1 已知二进制真值x=-0000，求其补码.

解 x共 5位：符号位为 1位，数值位 n为4，则

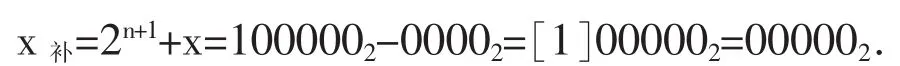
补码基于 “同余” 概念， 此处模为 2n+1= 1000002应丢掉，即最高位［1］应该丢掉,故其结果为 00000.该数连同符号位一起共5位数.这就是上述提到的对定义域“端点”之值进行处理的问题.结果说明，在补码系统中，0有唯一的表示，即+0=-0=0.但获得相同结果的实现方法是不同的.

例2 已知二进制真值x=-000,-001…-111, -1000，求其对应的补码.

解 x的前 8个数中,数值位n=3；后 1个数中，数值位n=4，则

当x=-000～-111时,由定义5第二段求得并简记为

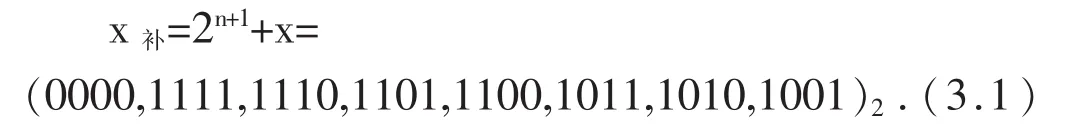
当x=-1000时,可根据定义5第三段求得

当x=-1000时,又可根据定义5第二段求得

把已知真值转换成其它编码,都可用相应定义求得,并可将所得结果制成表格,如表 1.该表十分直观地反映了真值与相应编码的对应关系，从例题和表 1可知：1000.因 为 -1000补=2n+1+x=1000002-10002= 110002，此处“模”为 100000，不可仿效例 1，这与实际是相悖的.

表1 四位二进制整数真值与原码、反码、补码和移码的对应表

4 结论

1）本文给出了四种编码的精确定义及其定义域，据此可求得任何真值的机器数.

2）补码和移码的定义分别由三段和二段函数组成,克服了以往补码用二段定义式、移码用一段定义式无法求出定义域端点处的编码值问题.

3）在定义域中，对 0标明了“+0”或“-0”，以示相应编码中，0的两种求取方法和表示形式，这样不但一目了然，还有警示作用.对“±0”，其补码和移码都有唯一的表示，但求取的方法则不同；“±0”的原码和反码，求取方法和表示形式均不相同.

4）必须说明：在求一个给定真值的相应编码时,通常是根据定义产生的“规则”去求的.对机器数编码的定义确实存在 “理论含糊纷乱”、“定义不精准”的问题，并似有续衍之势，导致了少数编码值无法用定义求取,也难于用 “规则”实现，笔者以为不妥.本文的目的是澄清并纠正这些问题，维护定义的严格性和精准性.

［1］Yarbrough,John M..Digital Logic Applications and Design.Original copyright 1997 by PWS Publishing Company, 28～32

［2］周南良.数字逻辑［M］.长沙：国防科技大学出版社, 1992,10-16

［3］毛法尧.数字逻辑［M］.北京：高等教育出版社, 2001,10-17

［4］王克义.数字逻辑［M］.北京：北京大学出版社, 1999,15-18

［5］王爱英.计算机组成与结构［M］.北京：清华大学出版社,1999,27-32

［6］俸远祯,阎慧娟,罗克露.计算机组成原理［M］.北京：电子工业出版社,1996,27-31

［7］王茜等,数字逻辑［M］.北京：人民邮电出版社,2011.

［责任编辑：刘向红］

Discussion on the Definition Problem of Several Codes in Digital Systems

QIU Hongwei
（Guangzhou College of Technology and Business，Guangzhou Guangdong 510850）

In this paper,the definitions and their definition domain problems of the machine codes.(true form, radix-1 complement,radix complement and frame shift)for binary and decimal in digital systems were discussed. The precise definition for these codes were provided,and explained by some examples.

truth value;true form;radix-1 complement;radix complement and frame shift;problem of definition and its definition domain;precision definition

TP 393

A

1672-402X（2016）08-0008-03

2016-01-08

丘洪伟（1980-），男，广东梅州人，广州工商学院讲师，网络工程师.研究方向：计算机网络、计算机应用.