基于增强蚁群优化算法与排序的MIMO检测算法

2016-07-04叶卓映

重庆邮电大学学报(自然科学版) 2016年2期

关键词：误码率

叶卓映

(厦门城市职业学院电子与信息工程系，福建厦门 361008)

基于增强蚁群优化算法与排序的MIMO检测算法

叶卓映

(厦门城市职业学院电子与信息工程系，福建厦门 361008)

摘要：基于最大似然比的多输入多输出(multiple input multiple output,MIMO)检测算法的计算复杂度随着天线阵的规模呈指数级增加，提出一种计算复杂度较优的MIMO检测算法。采用基于对数似然比的排序QR分解技术将信道矩阵分解为正交矩阵与上三角矩阵，相应地修改信号的发射顺序，降低错误判断引起的错误传播效应；为传统人工蚁群优化算法的信息素更新策略引入负信息素概念，有效地控制系统的拥塞；根据优化路径的距离积累了信息素。该方法设计了基于负信息素的信息素更新策略，增加MIMO系统的拥塞控制能力，考虑信道的衰落本性，基于路径的距离积累信息素。为了测试该算法的性能，进行了多组对比实验，结果表明，误码率性能优于其他智能优化算法，且对于64×64等大规模天线阵，该算法的计算复杂度随天线规模增长较小。

关键词：蚁群优化；多输入输出系统；检测排序；计算复杂度；误码率

0引言

多输入多输出(multiple input multiple output,MIMO)系统采用2N×2N的天线阵发送与接收信号，MIMO具有较高的频谱、能量利用率，应用较为广泛[1]。若天线阵的规模较大，信号检测算法的复杂度呈指数级增加，因此，MIMO系统对信号检测的计算复杂度要求极高[2]。

文献[3]提出一种低复杂度最大似然(maximum likelihood,ML)信号检测算法——双向最大似然检测算法，该算法通过建立可双向最大似然检测的候选发射向量集来缩小ML向量的搜索范围，从而降低信号检测的复杂度。文献[4]提出了一种接近最优检测性能的低复杂度并行MIMO检测算法，该算法基于信道分组检测的思想，对通过受噪声干扰严重的子信道信号采用遍历所有空间映射点的方式进行检测，对其余信号则采用新的基于格基约减的线性并行检测算法进行检测。文献[5]提出了一种基于改进蚁群优化算法与减格辅助技术获得检测性能与计算复杂度的权衡，获得了较好的性能，称为格规约-蚁群优化(lattice reduction-ant colony optimization, LR-ACO)。文献[6]提出了一种基于改进粒子群优化的MIMO检测优化算法—修改的粒子群优化(changed particle swarm optimization, CPSO)，该算法在保持较低误码率的前提下，具有较低的计算复杂度。

文献[3]的算法针对2×2的天线阵，具有较好的效果，但是对于大规模天线阵效果较差。文献[4-6]的信号检测算法则可应用于大规模MIMO系统，但其性能仍有改进的空间。

本文针对MIMO系统的检测技术，为人工蚁群算法引入负信息素的更新策略，并采用基于对数似然比的排序QR分解技术对信号检测流程进行排序，提出了一种低误码率的MIMO信号检测算法。仿真试验结果表明，本文算法信号检测性能优于其他的MIMO信号检测算法。

本文算法与其他基于人工智能的优化算法差异主要有以下3点：①针对MIMO系统的拥塞控制，设计了基于负信息素的信息素更新策略；②采用排序的检测来降低错误传播现象；③考虑信道的衰落性质，基于路径的距离积累信息素。

1系统模型

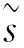
(1)

(1)式中:H表示Nr×Nt的信道矩阵；矩阵的元素{hj,i}设为均值为0、方差为1的复高斯分布，{hj,i}表示第i个发送天线与第j个接收天线之间信道的增益；n表示Nr×1大小的复高斯白噪声向量，其每个元素设为均值为0、方差为σ2的高斯分布。可将接收端的复数向量y转换为实数形式

y=Hs+n

(2)

(3)

(3)式中，Α表示信号星座图的实数分量，对于16-QAM信号，Α={-3,-1,1,3}。然后，可使用QR分解法将信道状态信息矩阵H分解处理，从而将(2)式改写为

y=QRs+n

(4)

QHy=QHQHs+QHn

(5)

(6)

(4)式中：Q表示2Nr×2Nt的正交矩阵；R表示2Nr×2Nt的上三角矩阵[8]。

上述模型对接收端的信道估算没有考虑误差，然而，对信道系数的估算存在不可忽略的误差，其误差模型可表示为[9]

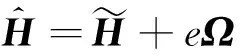
(7)

图1　离散MIMO系统模型Fig.1　Discrete MIMO system model

2基于改进蚁群优化的MIMO检测算法

2.1MIMO检测问题的模型

本文将MIMO检测问题建模为路径搜索问题，以便于使用蚁群优化算法求解。此外，本文借鉴文献[10]的旅行商问题(travellingsalesmnproblem,TSP)模型建立求解模型，可将MIMO的发送天线视为TSP问题中的城市，将第i个天线所有可能发出的信号看作到达第i个城市的可行路径。图2为借鉴TSP问题的MIMO检测的模型，表示了二进制相移键控(binaryphaseshiftkeying,BSPK)调制的4×4MIMO系统，问题可简化为搜索一次性遍历所有城市的最便宜解，即搜索最小化成本函数f(s)的向量s，成本函数可定义为

(8)

图2　BPSK调制的MIMO检测模型(Nt=Nr=4)Fig.2　BPSK modulated MIMO detection model(Nt=Nr=4)

2.2蚁群优化与本文方法

本文基于文献[7]的ACO算法进行增强，ACO使用一定数量的人工蚂蚁(Nants)搜索蚁窝N与食物源F之间的最短路径，如图3所示。其中，线条虚实线分别表示信息素浓度的高低。蚂蚁采用协同机制与环境交互，蚂蚁在N与F间移动时，在路径上洒下信息素，信息素随时间衰减，蚂蚁始终选择信息素最浓的路径，即从N开始、到达F的最短路径，其返回路径也选择该最短路径，导致同一条最短路径上积累的信息素增加较快。ACO是一种迭代搜索算法，在每轮迭代中，蚂蚁在其选择的路径上洒下信息素，每只蚂蚁检查路径中已有的信息素，根据之前蚂蚁选择最优路径。算法1为基本的蚁群算法流程。

图3　蚂蚁选择信息素最浓的路径Fig.3　Ants select the path with most pheromone

算法1蚁群优化算法。

初始化系统参数

WHILE未达到结束条件DO

建立蚁群解

局部搜索

更新信息素

ENDWHILE

在本文基于蚁群优化的MIMO信号检测中，使用人工蚁群搜索问题的解，设为Nants。假设共有M个到达目标城市i的路径(16-QAM的调制中，M=4)，将每条路径表示为sik(k=1,2,…,M;i=1,2,…,2Nt)。一个蚂蚁在每个路径sik上的移动表示了蚂蚁将符号sk选为第i个发送天线估算的信号。每轮迭代中，同时仅有一个蚂蚁移动，基于路径上的信息素浓度随机地搜索估算的发送向量。

每轮迭代选择最优向量的方法为

(9)

对(9)式进行扩展，可得

(10)

将路径sik到第i个城市的距离设为dik，即dik表示第k个路径至第i个城市的距离。

(11)

(12)

因为ηik与dik成反比，ηik随dik增加而降低，因此，积累的信息素将降低；而ηik随dik降低而增加，因此，累积的信息素将升高。

基于路径中的信息素浓度计算路径选择的概率，因此，路径选择概率pik的矩阵定义为

(13)

(13)式中，τik表示路径sik(蚂蚁的目标城市为i)的信息素等级(表示第i个天线发送的信号)。参数α是一个正的常量，表示了信息素等级的权重。当蚂蚁经过某条路径时，将信息素置于该路径中，基于当前的信息素等级更新路径的总信息素值。本文算法设计了一种新的信息素更新策略，本策略使用了负信息素。本信息素更新方法为

(14)

(14)式中，ρ∈(0,1]为一个常量，该常量用于减少对应路径的信息素，即控制路径中负信息素的量，以此实现拥塞控制。信息素基于参数ω积累，ω值不能设置过高，否则会导致早熟收敛且缩小搜索空间；ω值也不可设置过小，否则导致收敛速度过慢，因此，本文将ω设置较为适中。计算方法为

(15)

(15)式中，Δτik表示了路径sik上累积的信息素(第i个天线的第k个信号)。

因为本算法按顺序检测信号，所以，如果初始化阶段出现判断错误将导致剩余天线发送信号的检测错误，即错误传播现象。为了防止错误传播，本算法按顺序进行天线检测，本文使用文献[11]的基于对数似然比(log likelihood ratio,LLR) 的排序QR分解技术(sorted QR decomposition, SQRD)，将本文蚁群算法的信道矩阵H进行QR分解。算法2为本文算法，首先对输入参数进行初始化，执行LLR-SQRD算法将H分解为正交矩阵Q与上三角矩阵R，并且相应地修改信号的发射顺序，从而降低错误判断引起的错误传播效应。

本文算法与其他的人工蚁群优化算法存在3点主要差异：①针对MIMO系统的拥塞控制，设计了基于负信息素的信息素更新策略；②采用排序的检测来降低错误传播现象；③考虑信道的衰落性质，基于路径的距离积累信息素，如(15)式所示。

算法2本文蚁群优化的MIMO检测算法。

输入：y,H,Nt,Nant,α,ρ,ω

输出：最优解向量x(sol)

3x(int)：初始化解向量

4 WHILEj≤NantDO

5FORi≤2NtDO

6 FORk≤MDO

10END FOR

11FORk≤MDO

12 计算Δτik

13τik=τik-ρτik+ωΔτik//更新信息素

14ENDFOR

15 ENDFOR

18x(sol)=x(j)// 最优解向量

19x(int)=x(j)

21 ELSE

22x(sol)=x(int)

23 ENDIF

24ENDWHILE

3仿真实验与结果分析

对本文算法进行仿真实验，测试了算法的误码率性能、算法的计算复杂度变化情况。实验中，MIMO系统均采用4-QAM，天线阵分别设为6×6，8×8，16×16，32×32。假设本文算法中H的元符合均值为0、方差为1的高斯分布。基于MATLAB进行仿真，每组实验共计数2 000个错误比特来获得平均误码率。

3.1误码率性能的比较

首先，将本文算法与LR-ACO，CPSO，基本ACO算法的误码率进行比较，结果如图4、图5所示，其天线阵为6×6。从图4可看出，本文算法优于其他3种算法，在10-3的误码率处，本算法的信噪比比LR-ACO高出5dB左右，且明显优于其他2种算法，从图5中可看出，本算法也具有明显优势。本文的排序检测、负信息素方案有效地控制了系统拥塞以及错误传播效应，从而获得了较低的误码率性能。

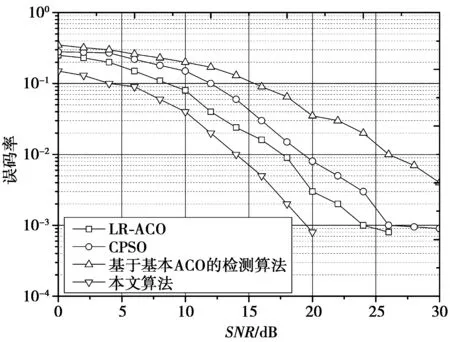
图4　4-QAM与6×6天线阵下的误码率比较Fig.4　Bit error rate for 4-QAM and 6×6 antenna matrix

图5　4-QAM与8×8天线阵下的误码率比较Fig.5　Bit error rate for 4-QAM and 8×8 antenna matrix

然后，测试了蚁群大小与信道估算误差(e)对算法性能的影响，结果分别如图6和图7所示。可看出，蚁群大小越大，算法的优化性能越好，误码率越低。从图7中可看出，算法的误码率性能与蚂蚁数量Nants的关系，对于SNR=14dB,Nt=Nr=8，16，32,3种情况，结果可看出，0≤Nants≤250下的误码率变化比Nants≥300剧烈，可基于目标误码率来设置本算法的蚁群大小。同时亦可看出，天线数量越多，收敛速度越快。

3.2计算复杂度性能分析

图8为本算法的计算复杂度与天线数量的关系,图8中,比较了8×8,32×32,64×64,3种天线阵下排序与未排序的计算次数比较,结果可看出,当Nants较小时,排序算法对本算法的计算复杂度有少量的影响,当Nants较大时,则几乎无影响。此外，天线越多，计算复杂度越高。

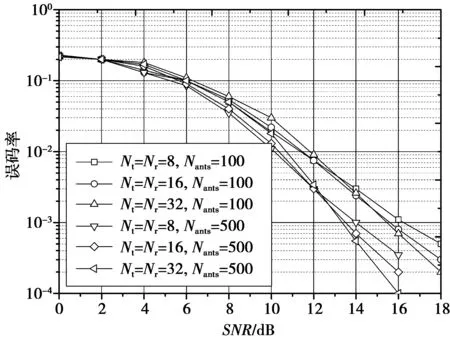
图6　4-QAM下8×8,16×16,32×32的MIMO系统(蚁群大小为100,500)Fig.6　Bit error rate of 8×8,16×16,32×32 MIMO system for 4-QAM(ant colony size is 100 and 500)

图7　Nt=Nr=8,16,32,SNR=14 dB,4-QAM的MIMO系统收敛性分析Fig.7　Converge analysis for MIMO system for Nt=Nr=8,16,32,SNR=14 dB,4-QAM

图8　4-QAM,SNR=14 dB下计算复杂度与蚁群大小的关系Fig.8　Relationship between computational complexity and ant colony size for MIMO system with 4-QAM,SNR=14 dB

4结论

本文针对MIMO系统的检测技术，为人工蚁群算法引入负信息素的更新策略，并采用基于对数似然比的排序QR分解技术对信号检测流程进行排序，提出了一种低误码率的MIMO信号检测算法。本文设计的信息素更新策略充分考虑了MIMO系统的拥塞控制，是网络保持较低的拥塞，从而进一步降低系统的误码率。最终，本算法获得了较好的误码率性能，且对于大规模的天线阵，本算法的计算复杂度增长较慢，具有一定的优势。

未来，将针对人工蚁群算法的收敛速度做进一步研究，以期在保持较高误码率性能的同时，加速收敛，从而进一步降低算法的复杂度。

参考文献：

[1]陈发堂, 侯彦庄. 基于MIMO-OFDM系统的一种低复杂度球型译码检测算法[J]. 计算机应用研究, 2011, 28(9):3436-3438.

CHEN Fatang,HOU Yanzhuang.Low complexity sphere decoding detection algorithm based on MIMO-OFDM system[J].Application Research of Computers,2011,28(9):3436-3438.

[2]郑俊松, 周晓方. 一种格缩减辅助MIMO检测的组合量化误差校正方法[J]. 小型微型计算机系统, 2013, 34(8):1926-1929.

ZHENG Junsong, ZHOU Xiaofang.Quantization Error Correction Scheme for Lattice-reduction Aided MIMO Detection[J].Mini-micro Systems,2013,34(8): 1926-1929.

[3]赵新雪, 李琼, 肖维杰,等. 低复杂度最大似然MIMO信号检测算法[J]. 计算机工程与设计, 2014, 35(1):144-147.

ZHAO Xinxue, LI Qiong, XIAO Weijie, et al. Low-complexity ML signal detection algorithm for MIMO system[J]. Computer Engineering and Design, 2014, 35(1):144-147.

[4]芮国胜, 张海波, 张洋,等. 接近最优检测性能的低复杂度线性并行MIMO检测算法[J]. 通信学报, 2013(2):8-14.

RUI Guosheng,ZHANG Haibo,ZHANG Yang,et al. Low complexity linear parallel detection algorithm for near ML detection of MIMO systems[J].Journal on Communications,2013(2):8-14.

[5]MARINELLO J C, TAUFIK A. Lattice Reduction Aided Detector for MIMO Communication Via Ant Colony Optimisation[J]. Wireless Personal Communications, 2014, 77(1):63-85.

[6]KNIEVEL C, HOEHER P A. On Particle Swarm Optimization for MIMO Channel Estimation[J]. Journal of Electrical & Computer Engineering, 2012, 2012(9):1-10.

[7]DORIGO M, STÜTZLE T. Ant Colony Optimization: Overview and Recent Advances[J]. International, 2010, 17(5):227-263.

[8]HENRICI P. Bounds for iterates, inverses, spectral variation and fields of values of non-normal matrices[J]. Numerische Mathematik, 1962, 4(1):24-40.

[9]AU E K S, WANG C, SFAR S, et al. Error probability for MIMO zero-forcing receiver with adaptive power allocation in the presence of imperfect channel state information[J]. IEEE Transactions on Wireless Communications, 2007, 6(4):1523-1529.

[10] LAIN J K, CHEN J Y. Near-MLD MIMO Detection Based on a Modified Ant Colony Optimization[J]. Communications Letters IEEE, 2010, 14(8):722-724.

[11] KIM S. Transmit Antenna Selection for Spatial Multiplexing UWB MIMO Systems Using Sorted QR Decomposition[J]. Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences, 2012, 95(E95.A):1426-1429.

Enhanced ant colony optimization and ordering based MIMO system symbol detection algorithm

YE Zhuoying

(Department of Electronics and Information Engineering, Xiamen City University, Xiamen 361008, P.R. China)

Abstract:Maximum likelihood MIMO(multiple-input-multiple-output) detection algorithm has best symbol detection performance, but it’s computation complexity increases in exponential order with the scale of antenna matrix, so a MIMO detection algorithm with lower computational complexity is proposed for that problem. Firstly, log maximum likelihood based sorted QR decomposition algorithm is used to decompose channel matrix into an orthonormal matrix and the upper triangular matrix, and the transmit order is changed accordingly, and the error propagation is improved by error decision; then, negative pheromones are introduced to ant colony algorithm, and the system congestion is controlled efficiently; lastly, the pheromones are updated according to the distance of the path. The negative pheromone based pheromone updating strategy is designed to improve the ability of congestion control, and considering the faded character of channel, the pheromone is accumulated based on the distance of the path. Some compared simulation experiments are setup to test the performance of the proposed algorithm. The results show that, the bit error rate performance of the proposed algorithm is better than other artificial intelligence algorithm; the computation complexity of the proposed algorithm increase is lower with antenna number for big scale antenna matrix.

Keywords：ant colony optimization; multi-input multi-output system; detection order; computation complexity; bit error rate

DOI：10.3979/j.issn.1673-825X.2016.02.004

收稿日期：2015-06-23

修订日期：2016-03-06通讯作者：叶卓映ye_zhuoying@163.com

基金项目：厦门城市职业学院科研项目(KYKJ2015-4)

Foundation Item：The Scientific Research Project of Xiamen City University (KYKJ2015-4)

中图分类号：TN914;TP393

文献标志码：A

文章编号：1673-825X(2016)02-0162-06

作者简介：