欧式复杂任选期权定价公式推广

王海叶

（宁德师范学院数学系，福建宁德352100）



欧式复杂任选期权定价公式推广

王海叶

（宁德师范学院数学系，福建宁德352100）

摘要：在股票价格服从对数正态分布的条件下，利用热传导方程，对系数是常数的标准任选期权的价值进行扩展，得到当无风险利率和股价的波动率随机时，任意时刻任选期权价值的计算公式.

关键词：欧式任选期权；对数正态分布；热传导方程；股票看涨；股票看跌

任选期权的持有者经过一段时期T，能选择是看涨或是看跌期权.标的两个期权的执行价格和期满日可以一样也可以不一样，如果一样则称为标准任选期权.如果任选期权基于的两个期权执行价格和到期日都不一样，则称为复杂任选期权.如果任选期权标的两个期权都是欧式的，则称欧式复杂任选期权. Rubinstein推导了欧式标准任选期权的价值，文献［1］研究了分数布朗运动下欧式复杂任选期权的定价，并通过数值模拟验证了它的合理性，文献［2］假定股票价格服从分数跳-扩散运动，推导了欧式复杂任选期权的解析定价公式，但这些模型的系数都是常数.而模型中系数无风险利率和股价波动率都是变化的，因此有必要建立一个更加合理的市场模型.本文在Rubinstein研究基础上，假设系数随时间变化，应用热传导方程，推导原生资产为股票，在任意时刻t∈［0， T］的欧式复杂任选期权价值的计算公式.

假设对于欧式任选期权，其持有者做出选择的日期为T，基于标的股票看涨期权，其行权价格是K1，期满日是T1≥ T；标的股票看跌期权，其行权价格为K2，期满日为T ≥ T.股价的变化用随机微分方程表示因此，欧式复杂任选期权，在T时刻的价值为这里表示在T时刻股票看涨期权的价值，而）表示在T时刻股票看跌期权的价值.

1　欧式复杂任选期权的价值

引理1［3］1）假设欧式任选期权标的股票看涨期权，其行权价格为K1，期满日为T1≥ T，基于标的股票看跌期权，其行权价格为K2，期满日为T2≥ T，则仅存在一个S*＞0，使成立；2）Bch（ T，ST）=

引理2［4］已知热传导方程满足u（0， x）=φ（ x），则

引理3［5］可表示为即N（ h，k； ρ）.这里ρ是二维正态分布中变量的相关系数，N（ h，k； ρ）是联合分布.

定理1假设原生资产为股票，当无风险利率、股价的波动率变化时，则在任意时刻t∈［0， T］，欧式复杂任选期权的价值为

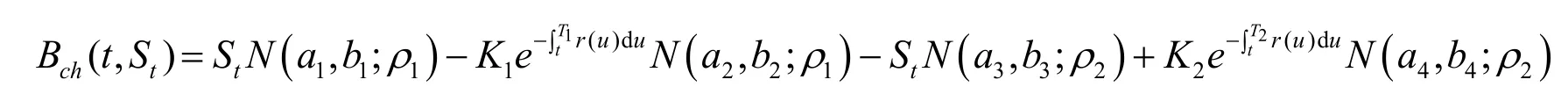
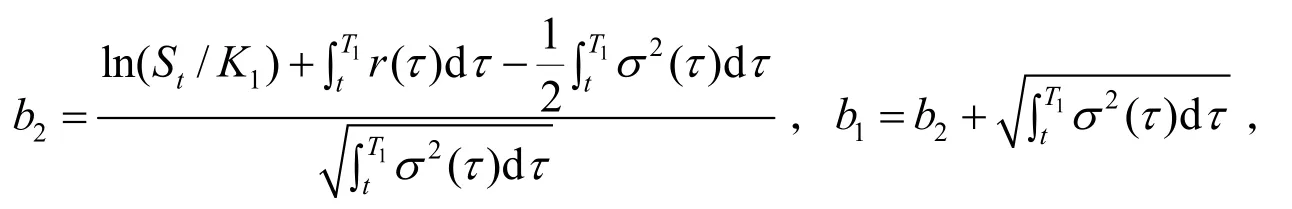
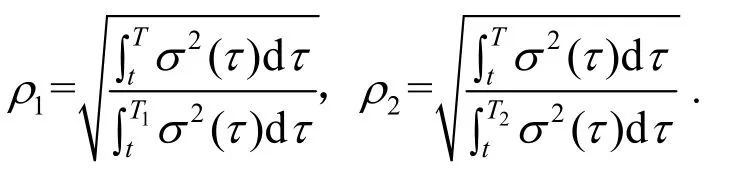
证明：设股价行为服从

其中zt遵循维纳过程.

由Black-Scholes方程可得标的期权的价值

其中（）

r t为无风险利率.

在T1时刻，股票看涨期权的收益为

方程（2）和（3）的解为［6］

在T2时刻，股票看跌期权的收益为

方程（2）和（4）的解为：

欧式任选期权在时刻T的收益为

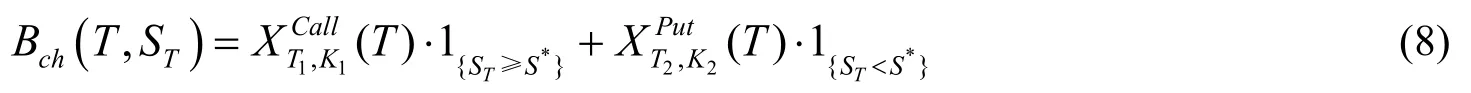
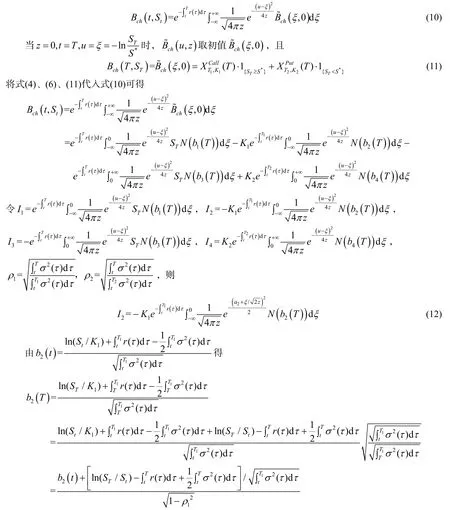
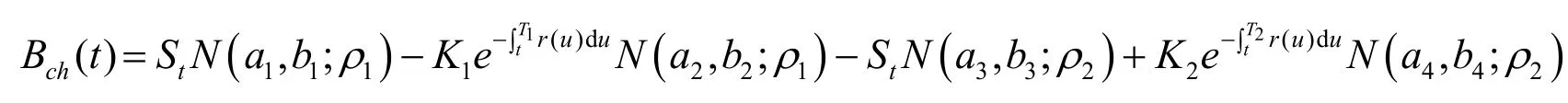
2　结语

假设标的资产股价服从对数正态分布，在无风险利率、股价的波动率变化的市场模型中，将任选期权满足的微分方程转化为热传导方程，推导得出原生资产为股票时，在任意时刻t∈［0， T］，欧式复杂任选期权价值的计算公式.

参考文献：

［1］詹颖心，徐云.分数布朗运动下欧式复杂任选期权定价［J］.数学理论与应用，2010，30（3）∶78-82.

［2］牛淑敏，徐云.分数跳-扩散运动下欧式复杂任选期权定价［J］.数学理论与应用，2012，32（2）∶39-46.

［3］KORN RALF，KORN ELKE. Option Pricing and Portfolio Optimization∶Modern Methods of Financial Mathematics［M］.［S. l.］∶American Mathematical Society，2000.

［4］STOJANOVIC SRDJAN. Computational Financial Mathematics using mathematica∶Optimal Trading in Stocks and Options［M］. Boston∶Birkhuser，2003.

［5］GESKE R. The valuation of corporate liabilities as compound options［J］. Journal of Financial & Quantitative Analysis，1977，12（4）∶541-552.

［6］MERTON R C.Application of option-pricing theory∶twenty-five years later［J］. The American Economic Review，1998，88（3）∶323～349.

(责任编辑：饶超)

Promotion of Pricing Formula for European Complex Chooser Options

WANG Haiye
（School of Mathematics，Ningde Normal University，Ningde 352100，China）

Abstract∶On condition that the stock price obeys lognormal distribution，using the heat conduction equation，the value of standard chooser options with constant coefficient is generalized，the calculation formula of the chooser optional value at any moment is derived when the risk-free rate of interest rate and stock price volatility is random.

Key words:European chooser options；Lognormal distribution；Heat conduction equation；Stock call option；Stock put option

中图分类号：O22

文献标志码：A

文章编号：2095-4476（2016）05-0005-04

收稿日期：2016-03-24

基金项目：宁德师范学院青年教师专项课题（2014Q62）

作者简介：王海叶（1981—），女，山西朔州人，宁德师范学院数学系讲师.