基于Taylor-Edgeworth级数的结构可靠性分析*

孟广伟　冯昕宇　周立明　李锋

(吉林大学 机械科学与工程学院， 吉林 长春 130025)

基于Taylor-Edgeworth级数的结构可靠性分析*

孟广伟冯昕宇周立明李锋†

(吉林大学 机械科学与工程学院， 吉林 长春 130025)

摘要:为了解决工程实际中高维非线性或功能函数为隐式的情况给结构数值分析带来的困难，文中提出了一种新型结构可靠性直接分析方法.首先利用降维算法将维函数展开为个一维函数的形式，再将各一维函数中的变量运用变量转换方法进行变换，并结合Gauss-Hermite数值积分方法，计算得到个一维函数的原点矩及中心矩，将所得矩信息与Taylor展开计算出的结构功能函数的中心矩结合，再借助Edgeworth级数法推导出结构功能函数的累积分布函数表达式，并运用结构可靠性理论计算得到结构功能函数的失效概率.该方法在计算过程中无需进行多重积分计算功能函数的统计矩.数值算例结果表明该方法正确可行.

关键词：结构可靠性；降维算法；Taylor展开；Edgeworth级数；矩方法

目前工程结构可靠性分析[1- 3]大多数采用概率统计理论进行研究，且研究的主要内容之一是求解结构的失效概率，但在多数工程实际问题中无法明确获得显式结构功能函数或所得功能函数的非线性程度较高.通常情况下运用数值计算方法来计算结构的响应,但在具体求解过程中时会遇到各种困难.例如，梯度计算的可靠性分析方法，传统的一次二阶矩法[4]和二次二阶矩法[5]，结构功能函数为隐式或在验算点附近的非线性程度较高，很难获得梯度函数而难以实施；对于基于数字模拟的可靠性分析方法，如蒙特卡洛法[6- 7]等，由于其不断模拟结构响应的工作量太大使得其在工程实际中的应用范围受到一定的限制；对于基于构建拟合真实函数的可靠性方法，如响应面法[8- 9]和人工神经网络方法[10- 11]等，前者受到函数形式和抽样点位置的限制，后者受到参数选择、局部最优、拓扑结构等因素的限制.

有鉴于此，文中结合降维算法、变量转换法、Gauss-Hermite数值积分、Taylor展开及Edgeworth级数[12- 13]进行结构的可靠性分析.采用降维算法，将n维函数展开为n个一维函数，利用变量转换法与Gauss-Hermite数值积分计算得到n个一维函数的原点矩及其相应的中心矩，且由Taylor展开计算得到结构功能函数的统计矩信息，再将所得的前4阶中心矩作为系数代入到Edgeworth级数展开式中，从而计算得到结构的失效概率.最终，利用算例验证了文中方法的正确性与合理性.

1降维算法

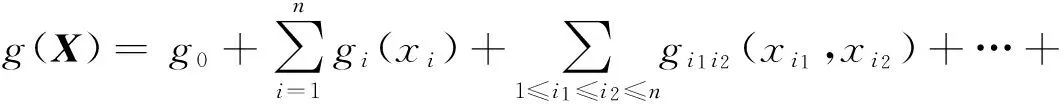
g12…n(x1,x2,…,xn)

(1)

式中，g0为常量，gi(xi)仅为变量xi对函数的一阶表达，gi1i2(xi1,xi2)为变量xi1和xi2两者共同对函数作用的二阶表达，gi1i2…ik(xi1,xi2,…,xik)为前k阶项共同对函数作用的表达，g12…n(x1,x2,…,xn)为所有变量共同对函数作用的表达.

为不失一般性，任取空间中的任意一个参考点c={c1,c2,…,cn}，而仅考虑式(1)的一阶项，则所得函数可由下式表达为

gi(xi)=gi-g(c)

(2)

式中，gi=g(c1,c2,…,ci-1,xi,ci+1,…,cn).文献[16]中指出参考点c的最优点值为各变量的均值，则式(2)中的g(c)，μxi为xi的均值.gi可分别改写为g(c)=g(μx1,μx2,…,μxn)、gi=g(μx1,μx2,…,μxi-1,μxi,μxi+1,…,μxn).

由此知n维函数g(X)的单变量(降维)表达形式也可由n个一维函数g(xi)来表达，可写为

(3)

式中：g(xi)=g(μx1,…,μxi-1,xi,μxi+1,…,μxn)，为一维函数；g(x0)=g(μx1,μx2,…,μxi,…,μxn)，为常数项.

2一维函数的统计矩

由式(3)得到功能函数的单变量近似表达，可通过传统的直接高斯积分方法求解一维函数g(xi)的统计矩信息，但在计算过程中会带来较大的误差.

不失一般性地任意选取一组相互独立且分布类型不限的向量X=[X1,X2,…,Xn]T转换成一组服从正态分布且独立的向量U=[u1,u2,…,un]T.经转换后可得

(4)

式中,Φ-1[*]为标准正态分布的累积分布函数的逆函数，变量Xi的累积分布函数为FXi(Xi).经转换后的概率密度函数fUi(ui)和累积分布函数FUi(ui)可分别表达为

(5)

(6)

(7)

式中，ωi为高斯权重，f(xi)为xi的概率密度函数，k为矩的阶数.

因而，文中在计算一维函数g(xi)的统计矩时，首先将变量均转换为服从N(0,0.5)的变量，即可不受到变量分布类型的限制，再选用Gauss-Hermite数值积分方法推导出式(7)，避免了传统的高斯积分的指数项带来的计算误差.

由式(7)计算得到一维函数的各阶原点矩，借助于中心矩与原点矩间关系式，可得一维函数前四阶中心矩表达式为

(8)

(9)

(10)

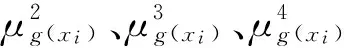
3功能函数的统计矩

在得到各一维函数的统计矩后，文中借助于Taylor展开，并且仅展开其至1阶项，其他阶次项所带来的误差暂且不计，可得n维函数Z=g(X)的前四中心阶矩表达式.

一阶矩(均值)表达式为

(11)

式中,E[·]为期望算子.

二阶中心矩(方差)表达式为

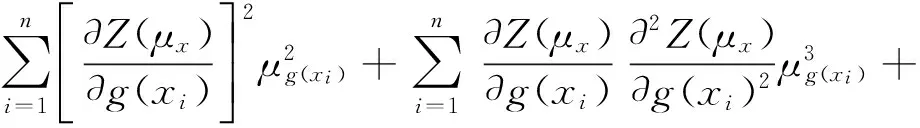
(12)

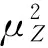
三阶中心矩(偏度)表达式为

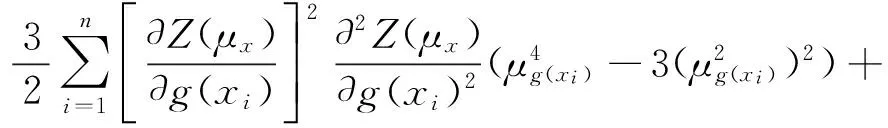
(13)

四阶中心矩(峰度)表达式为

(14)

4Edgeworth级数

由式(11)-(14)得到结构功能函数的前四阶中心矩后，Edgeworth级数可以任意精确地逼近随机变量的真实分布，且通常取其前4项便可获得较好的精度，将四阶矩作为Edgeworth级数展开式中的系数来拟合功能函数相应的累积分布函数F(g)及其概率密度函数f(g).

由Edgeworth级数展开法知，结构功能函数的概率密度函数f(g)和累积分布函数F(g)可分别表达为

(15)

结合矩方法与Edgeworth级数展开式来拟合功能函数相应的累积分布函数，简化了求解的复杂程度.

5数值算例

5.1算例1

考虑一个乘积形式的非线性功能函数g(x1,x2,x3,x4)，4个随机变量相互独立，计算其失效概率.随机变量统计参数见表1.功能函数为在结构可靠度计算中，蒙特卡洛(MCS)被认为是一种准确的计算方法，可将其结果作为精确解来进行对比，在文中未给出相对误差比较.文中方法计算的失效概率相对误差仅为0.56%，与MCS结果偏差较小.表2中列举了采用其他几种计算方法的结果，通过表2的比较，体现了文中方法的正确性与合理性，在计算精度方面也具有一定的优越性.

(17)

表1基本随机变量统计特征值

Table 1Statistical characteristic values of basic random variables

随机变量分布类型均值变异系数偏态系数峰度系数x1正态1.20.3003x2正态2.40.0303x3正态50.00.0603x4正态25.00.3003

表2　算例1的失效概率结果

5.2算例2

自行车车架的尺寸和关键点的位置如图1所示.其中泊松比μ=0.3，弹性模量E=0.7×109Pa，L1杆是车头前叉位置，3号点是车座位置，4号点是脚踏中轴位置，5号点和6号点是后轮所在位置，它们位于车架对称面的两侧，z3=50 mm，由这两点引出后叉水平杆L5和L6、后叉斜杆L7和L8，各杆件长如图1所示.利用空间管单元PIPE16，P1=750 N，P2=240 N.在节点3处施加竖直向下车架载荷P1，节点4处同时施加竖直向下脚踏载荷P2，参数统计特征值列于表3.自行车车架的屈服应力为σs,自行车车架的最大Mises应力为σ，可得到功能函数为

g=σs-σ

(18)

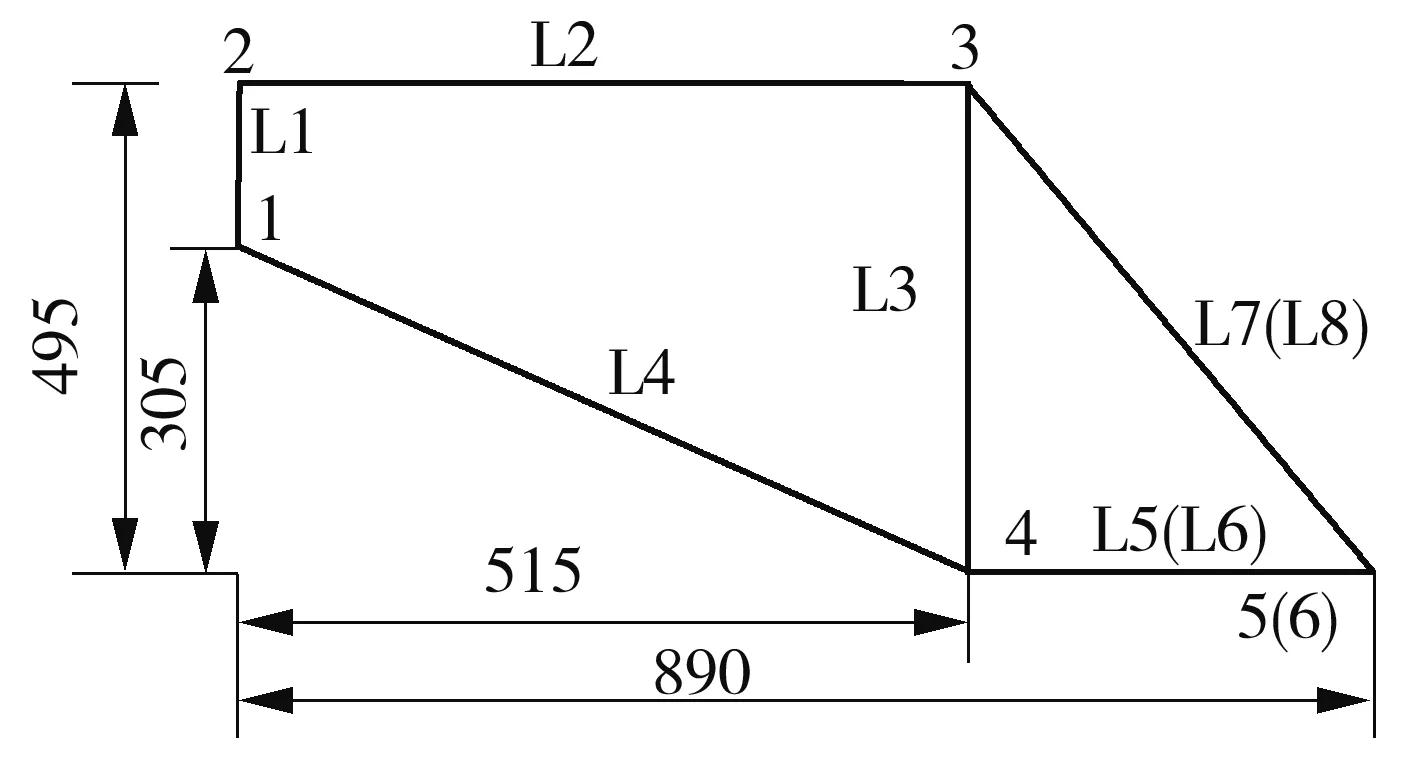
图1　自行车车架尺寸、关键点和线的布置

Fig.1Dimension of the bicycle and distribution of keypoints and lines

表3自行车车架参数统计特征值

Table 3Statistical characteristic values of the bicycle frame parameters

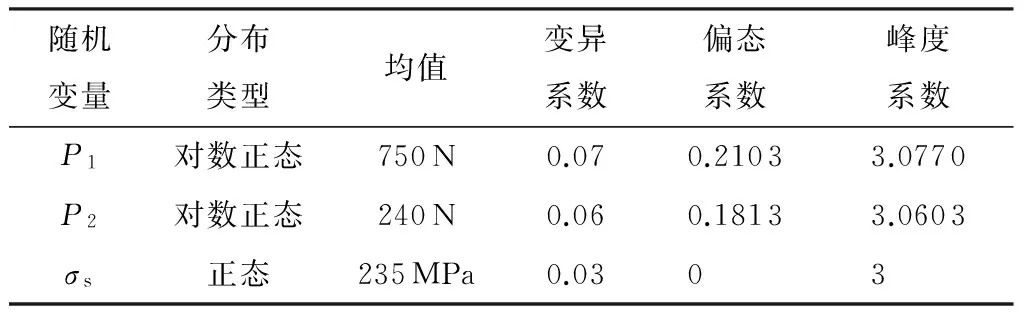
随机变量分布类型均值变异系数偏态系数峰度系数P1对数正态750N0.070.21033.0770P2对数正态240N0.060.18133.0603σs正态235MPa0.0303

文中首先由式(1)可知，n维结构功能函数g(X)可由单变量降维表达式来近似表达，为计算其统计矩信息，则需结合变量转换法和Gauss-Hermite数值积分方法计算一维函数g(xi)的原点矩及其相应的中心矩信息，调用自行车车架结构的有限元程序，即获得自行车车架的最大Mises应力的样本点，再运用Taylor级数推导出的式(11)-(14)来计算结构功能函数的前四阶中心矩，借助Edgeworth级数展开法将所得的统计矩信息作为系数代入式(16)，可得自行车车架最大Mises应力(即结构功能函数)的累积分布函数及结构的失效概率.

由式(18)给出的自行车车架结构的功能函数为隐函数，不能通过基于梯度计算的FORM与SORM来直接计算获得式(18)的梯度.文中利用ANSYS软件中的PDS模块进行有限元分析，采用MCS直接抽样方法并与之相比较，抽样次数为2×105次，所需计算时间为45 950.844 s，而文中方法仅需0.489 7 s,重分析次数为9；文中方法的失效概率为0.004 8，MCS的失效概率为0.004 9，相对误差仅为0.184%.图2为自行车车架实体模型.该算例方法实现简单，计算功能函数的前四阶中心矩结果列于表4，图3为其与MCS法对比的概率密度函数图，图4为其与MCS法对比的累积分布函数图,从上图中可看出文中方法与MCS法的吻合度较好.

图2　自行车车架实体模型

中心矩MCS文中方法相对误差/%一阶35.096935.09480.006二阶170.4425170.44830.003三阶-256.4940-253.41931.198四阶8.8209×1048.7344×1040.980

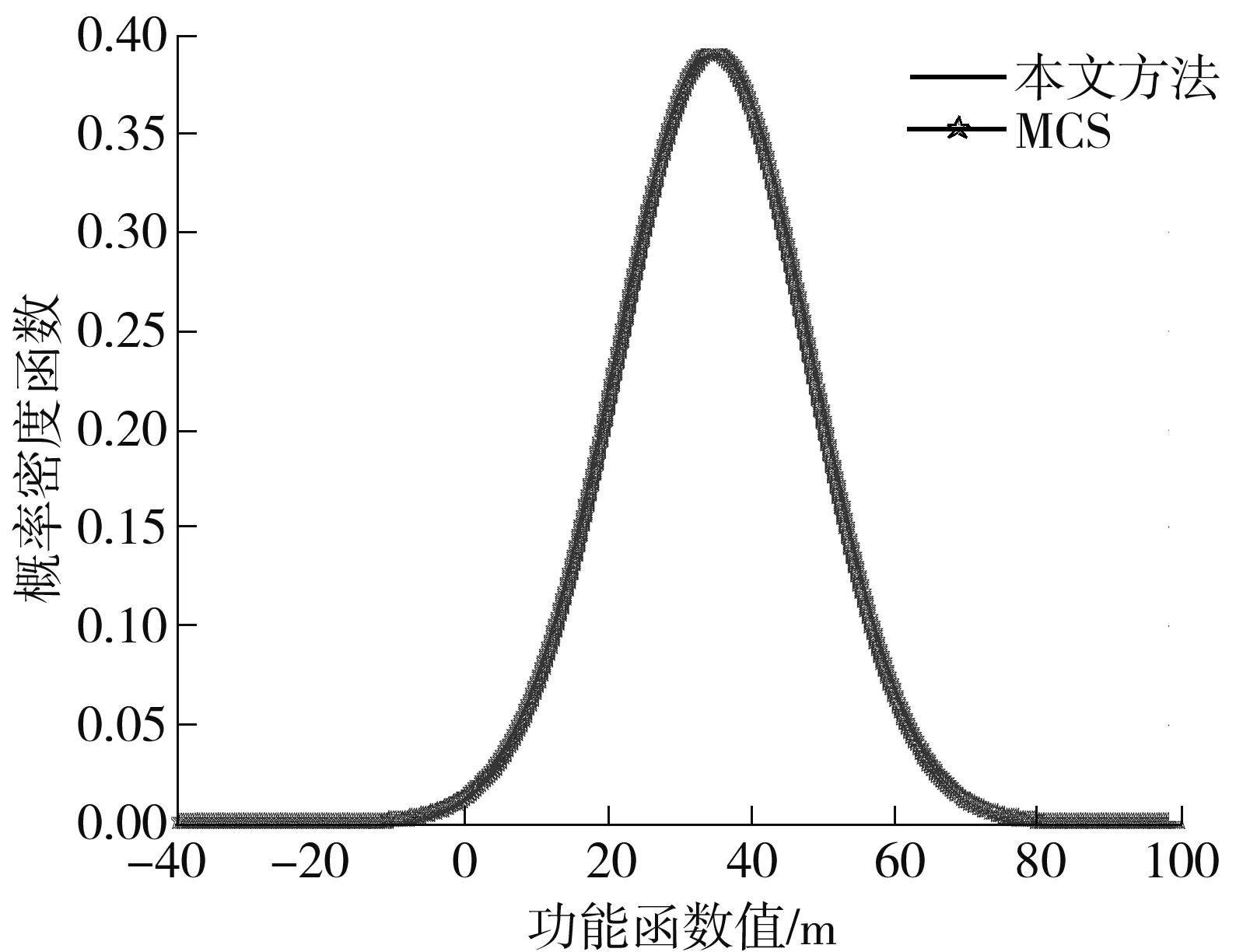
图3　功能函数的概率密度

文中方法在计算过程中无需进行多重积分的计算，无需求解功能函数的逆矩阵，无需寻找结构的最可能失效点，说明该方法具有正确性和可行性.

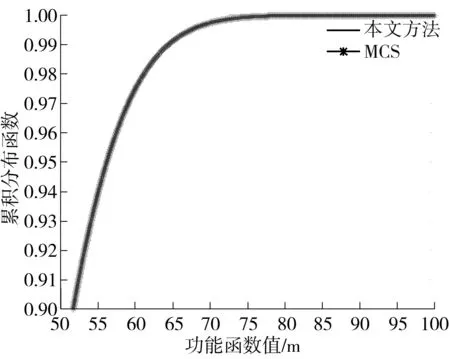
图4　功能函数的累积分布

6结论

文中提出了一种基于降维算法、变量转换法、Gauss-Hermite数值积分方法、Taylor级数及Edgeworth级数展开法的直接结构可靠性分析方法.降维算法变繁为简,可以降低多重积分的工作量,无需求解功能函数的逆矩阵;变量转换法、Gauss-Hermite数值积分方法相结合保证了一维函数的统计矩信息的计算精度;利用Taylor级数推导并简化了功能函数统计矩的求解;借助于Edgeworth级数展开法与所得统计矩信息可推导出结构功能函数的累积分布函数.文中方法降低了多重积分的工作量,简化了结构功能函数统计矩的求解过程,算法简单且易于编程.数值算例结果表明文中方法具有正确性与合理性.

参考文献：

[1]郑灿赫,孟广伟,李锋,等.基于 PSO-DE 混合算法的结构可靠性优化设计 [J].华南理工大学学报(自然科学版),2014,42(9):41- 45.

ZHENG Can-he,MENG Guang-wei,LI Feng,et al.Structural reliability-based optimization design using PSO-DE hybrid algorithm [J].Journal of South China University of Technology(Natural Science Edition),2014,42(9):41- 45.

[2]李方义,荣见华,胡林,等.基于概率-凸集混合模型的汽车正面碰撞结构可靠性优化设计 [J].振动与冲击,2016,35(3):215- 220.

LI Fang-yi，RONG Jian-hua,HU Lin,et al.Reliability-based optimization design of structure subjected to vehicle frontal impact based on probability-convex hybrid model [J].Journal of Vibration and Shock,2016,35(3):215- 220.

[3]MELCHERS R E.Progression of pitting corrosion and structural reliability of welded steel pipelines [J].Oil and Gas Pipelines:Integrity and Safety Handbook,2015,7(23):327- 342.

[4]HUANG X Y,ALIABADI M H.A boundary element method for structural reliability [J].Key Engineering Materials,2015,627:453- 456.

[5]LOW B K,PHOON K K.Reliability-based design and its complementary role to Eurocode 7 design approach [J].Computers and Geotechnics,2015,65:30- 44.

[6]CHOI M J,CHO H,CHOJ K K,et al.Sampling-based RBDO of ship hull structures considering thermo-elasto-plastic residual deformation [J].Mechanics Based Design of Structures and Machines,2015,43(2):183- 208.

[7]MENG D,LI Y F,HUANG H Z,et al.Reliability-based multidisciplinary design optimization using subset simulation analysis and its application in the hydraulic transmi-ssion mechanism design [J].Journal of Mechanical Design,2015,137(5):051402.

[8]SHI X,TEIXEIRA A P,ZHANG J,et al.Structural reliability analysis based on probabilistic response modelling using the maximum entropy method [J].Engineering Structures,2014,70:106- 116.

[9]BAI Y,TANG J,XU W,et al.Reliability-based design of subsea light weight pipeline against lateral stability [J].Marine Structures,2015,43:107- 124.

[10]FERLITO S,ATRIGNA M,GRADITI G,et al.Predictive models for building’s energy consumption:an Artificial Neural Network(ANN) approach [C]∥Proceedings of AISEM Annual Conference.[S.l]:IEEE,2015:1- 4.

[11]MENTZ R J,BABYAK M A,BITTNER V,et al.Prognostic significance of depression in blacks with heart failure insights from heart failure:a controlled rrial investigating outcomes of exercise training [J].Circulation:Heart Failure,2015,8(3):497- 503.

[12]KONG C,SUN Z,NIU X,et al.Moment methods for C/SiC woven composite components reliability and sensitivity analysis [J].Science and Engineering of Composite Materials,2014,21(1):121- 128.

[13]LV C,ZHANG Y,WANG X,et al.Frequency reliability-based robust design of the suspension device of a jarring machine with arbitrary distribution parameters [J].Mechanics Based Design of Structures and Machines,2015,43(4):487- 500.

[14]RAHMAN S,XU H.A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics [J].Probabilistic Engineering Mechanics,2004,19(4):393- 408.

[15]CHO H,BAE S,CHOI K K,et al.An efficient variable screening method for effective surrogate models for reliability-based design optimization [J].Structural and Multidisciplinary Optimization,2014,50(5):717- 738.

[16]LI G,ZHANG K.A combined reliability analysis approach with dimension reduction method and maximum entropy method [J] Structural and Multidisciplinary Optimization,2011,43(1):121- 143.

Structural Reliability Analysis Based on Taylor-Edgeworth Series

MENGGuang-weiFENGXin-yuZHOULi-mingLIFeng

(School of Mechanical Science and Engineering, Jilin University, Changchun 130025, Jilin, China)

Abstract:In order to overcome the difficulties in structural numerical analysis caused by the high-dimension nonlinearity or the implicit performance functions in engineering practice, a numerical method to directly analyze the structural reliability is proposed. In this method, the n-dimension function is changed into n single-dimension functions via the dimension reduction, and the origin moment and the central moment of each single-dimension function are calculated through the variable transformation of the single-dimension functions and the Gauss-Hermite numerical integration. Then, the moment information is combined with the central moment of the structural performance function obtained by Taylor expansion, the cumulative distribution function of the structural performance function is deduced with the help of Edgeworth series, and the failure probability of the structural performance function is calculated based on the structural reliability theory. The proposed method avoids the multiple integrations for the statistical moment calculation of the performance function. Numerical examples show that this method is correct and feasible.

Key words:structural reliability; dimensionality reduction algorithm; Taylor expansion; Edgeworth series; moment method

收稿日期:2015- 09- 24

*基金项目:吉林省科技厅基金资助项目(201205001,201215048)；国家重大科学仪器设备开发专项(2012YQ030075)

Foundation item:Supported by the Jilin Provincial Department of Science and Technology Fund Project(201205001,201215048) and the National Key Scientifc Instrument and Equipment Development Projects(2012YQ030075)

作者简介:孟广伟(1959-)，男，博士，教授，主要从事疲劳与断裂研究.E-mail:mgw@jlu.edu.cn †通信作者: 李锋(1977-)，男，博士，副教授，主要从事疲劳与断裂研究.E-mail:fengli@jlu.edu.cn

文章编号:1000- 565X(2016)04- 0130- 05

中图分类号：TB 114.3

doi：10.3969/j.issn.1000-565X.2016.04.019