基于粒子群优化支持向量机的电缆温度计算*

牛海清　叶开发　许佳　吴炬卓　罗健斌　陆国俊

(1.华南理工大学 电力学院， 广东 广州 510640; 2.广州供电局有限公司电力试验研究院， 广东 广州 510410)

基于粒子群优化支持向量机的电缆温度计算*

牛海清1叶开发1许佳1吴炬卓1罗健斌2陆国俊2

(1.华南理工大学 电力学院， 广东 广州 510640; 2.广州供电局有限公司电力试验研究院， 广东 广州 510410)

摘要:导体温度是影响运行电缆使用寿命和材料利用率的最主要因素，也是反映电缆运行状态的参数.由于技术上尚难以实现对运行电缆导体温度的直接测量，因此有必要进行导体温度计算.文中以电流和外皮温度作为模型输入，以导体温度作为模型输出，构建基于支持向量机的电缆暂态导体温度的数学模型；为提高该模型计算的精度，避免盲目选取训练参数，引入粒子群算法对其惩罚因子C和核参数γ进行寻优.仿真与试验对比结果表明：基于粒子群优化的支持向量机模型(PSO-SVM模型)可以用于电缆暂态导体温度计算，且计算误差小于热路模型和BP神经网络；模型具有良好的泛化能力.

关键词：电缆；导体温度；支持向量机；粒子群优化；暂态计算

随着我国城市化进程的不断推进，新增电缆走廊日益困难，而用电负荷却不断提高，两者之间的矛盾日趋突出，因此确定准确的载流量从而最大化现有电缆线路输送能力正逐渐被电力企业所重视.如果载流量过大导致导体温度长期超过电缆主绝缘长期耐热温度，将直接影响到电缆的安全运行和使用寿命；如果载流量过小，电缆导体长时间低温运行，线芯材料没有得到充分利用[1- 3].载流量由电缆绝缘(与导体温度相同)的温度决定.由于结构上的原因，目前在技术上尚难实现对运行中电缆导体实时温度的直接测量，只能在监测外皮温度、环境温度、电流等的基础上进行计算[4- 5].因此对电缆导体温度计算方法进行研究具有重要的意义.

电缆实际运行过程中，对导体温度影响最大的负荷电流和周围环境温度都是实时变化的，这使得电缆导体温度总是处于暂态过程.电缆暂态导体温度计算方法主要有：根据IEC 60287和IEC 60853标准，采用热电类比的方法将电缆热传导过程类比电路模型建立电缆热路模型[6- 8]，进而运用数学方法从外皮温度反推出导体温度，该方法计算结果受到电缆本体传热参数及环境的影响；文献[9]中运用数值计算方法建立了电缆的理论热模型，模型同样面临传热参数难以确定的问题，此外，复杂运行情况下(如集群敷设)电缆的温度场是一个传导、对流、辐射3种传热方式的耦合过程，模型的构建复杂.近年来，已有研究人员应用人工智能方法建立电缆暂态导体温度模型，文献[10]中基于电缆实时外皮温度和运行电流，运用BP神经网络(BPNN)实时计算单芯电缆的导体温度.该方法具有较高的精度，且计算结果不受电缆本身参数和环境影响，然而，神经网络存在易陷入局部极小值、“过拟合”等方面的问题.而应用支持向量机(SVM)可以很好地克服神经网络的这些问题.

文中使用支持向量机建立电缆暂态导体温度计算模型，并引入粒子群算法(PSO)对模型的参数进行优化.

1电缆暂态导体温度计算原理

1.1支持向量机的基本思想

支持向量机是Vapnik及其合作者在研究统计学习理论中的VC维理论和结构风险最小化原则基础上提出的一种机器学习方法[11- 13]，它通过在模型的学习能力和复杂度之间寻求最佳结合点，克服了其他机器学习方法(如人工神经网络)过学习、欠学习、维数灾难、局部极小值等问题[14- 16].目前支持向量机已在小样本、非线性及高维模式识别等诸多领域中取得了良好效果[17- 19].

支持向量机的核心思想是通过非线性映射φ(x)函数将l个训练样本输入xi(i=1,2,…,l)映射到高维特征空间Hilbert，继而在高维特征空间中建立线性回归函数

f(x)=wφ(x)+b

(1)

式中，w为权值向量，b为偏置.最佳的w和b可使所建立的模型期望风险最小，而统计学习理论认为结构风险(由经验风险和表示模型复杂度的罚项组成)是期望风险的一个上界，因此极小化结构风险便可得到最优参数w和b：

(2)

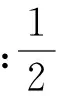
(3)

核函数k(xi,xj)为满足Mercer理论的任意对称函数，k(xi,xj)=φ(xi)φ(xj).选用不同的核函数可构造出不同的SVM.目前，应用较多的核函数有线性核函数、Sigmoid核函数、径向基核函数等，其中，径向基函数(RBF)表示形式简单，解析性好[20]，因此文中选用径向基函数作为核函数，其公式为

k(xi,xj)=e-γ‖xi-xj‖2

(4)

求解式(3)可得到由训练样本表示的w：

(5)

进而可求得非线性回归函数为

(6)

(7)

在构建支持向量机模型的过程中，惩罚因子C和核参数γ取值恰当与否直接决定了模型的性能.C太大或者γ太小易造成过学习而导致模型泛化性能变差，C太小或γ太大则易产生欠学习现象.为了得到性能最优的支持向量机模型，同时避免盲目选取训练参数，文中采用粒子群算法对支持向量机模型的惩罚因子C和核参数γ进行寻优.

1.2粒子群算法原理

粒子群算法是是由Eberhart和Kennedy提出的一种具有很强寻优能力的智能优化算法，其基本思想是通过个体之间的协作与竞争来实现多维空间的最优解搜寻[21- 25].

PSO首先在n维解空间初始化一个含有m个粒子的种群，每个粒子的位置都代表寻优问题中的一个可行解，粒子的优劣程度通过其对应的适应度值来表示.在寻优过程中，粒子根据式(8)、(9)进行迭代，更新自己在解空间中的飞行速度与空间位置并计算适应度值，直到满足迭代终止条件.

(8)

(9)

式中:N为当前迭代次数；i=1,2,…,m,表示第i个粒子；j=1,2,…,n,表示第j维空间；v为粒子的速度；x为粒子的位置；Pij为第i个粒子第j维空间的局部极值，Pgj为第j维空间的全局极值，ω为惯性权重系数，它使粒子保持运动惯性；c1和c2为两个学习因子，c1表示粒子对自身的认识程度，c2表示粒子对整个群体知识的认识程度；r1、r2为[0，1]的随机数.

1.3基于PSO-SVM的电缆暂态导体温度计算流程

采用粒子群算法与支持向量机相结合的方法对电缆暂态导体温度进行计算的流程如下.

步骤1确定合适的模型输入、输出

由于电缆内部热容的存在，导体温度不能发生突变，其变化总是滞后于电流变化.因此，为计算某一时刻的导体温度，需要考虑该时刻前小时的电流和外皮温度(与电缆的热时间常数有关)，因此文中以t-kΔt，t-(k-1)Δt，…，t-Δt共k个时刻的电流和外皮温度作为模型的输入，电缆t时刻导体温度作为模型的输出,其中Δt为15 min.

步骤2将训练样本输入及输出归一化

为加快训练程序的计算速度并消除量纲的影响，将输入及输出均按照式(10)归一化到[-1,1]区间：

(10)

步骤3PSO寻优SVM参数惩罚因子C和核参数γ

将训练样本均方误差(MSE)作为粒子群的适应度函数；初始化粒子群，基于训练样本用每个粒子的位置[C,γ]训练支持向量机回归模型，并计算适应度；根据式(8)和(9)更新粒子速度和位置，进行种群迭代，直至适应度值小于均方误差eMSE的阈值或者迭代一定的次数时，输出最优参数[C,γ]，其中，

(11)

步骤4根据步骤3得到的最优参数[C,γ]建立基于支持向量机的暂态导体温度回归计算模型.

步骤5暂态导体温度计算

将实时监测到的外皮温度和电流归一化后输入到训练好的支持向量机回归模型，进行暂态导体温度的计算，将计算结果反归一化即可得到实时导体温度.

2电缆温升试验

为研究文中所建基于PSO-SVM的电缆导体暂态温度计算模型的有效性及准确性，选取交联聚乙烯钢带铠装三芯电力电缆(型号为YJV22- 8.7/15- 3×240)分别进行电缆沟敷设单回路、排管敷设六回路电缆温升试验.考虑到热电偶的测量误差，在每根试验电缆中部选取3个截面(相邻截面之间距离1 m)，并用电钻在每个截面针对三相导体钻3个孔，将热电偶插入到孔洞直至与导体接触；在每根电缆表面敷设4个热电偶测量其外皮温度[2].实际负荷调度中一般每15 min改变一次电流值，因此试验过程中每隔15 min采集一次温度和电流数据.将导体温度平均值和外皮温度平均值作为后续分析的依据，图1(a)为电缆沟敷设单回路的试验结果，图1(b)为排管敷设六回路中温度最高的电缆的试验结果.

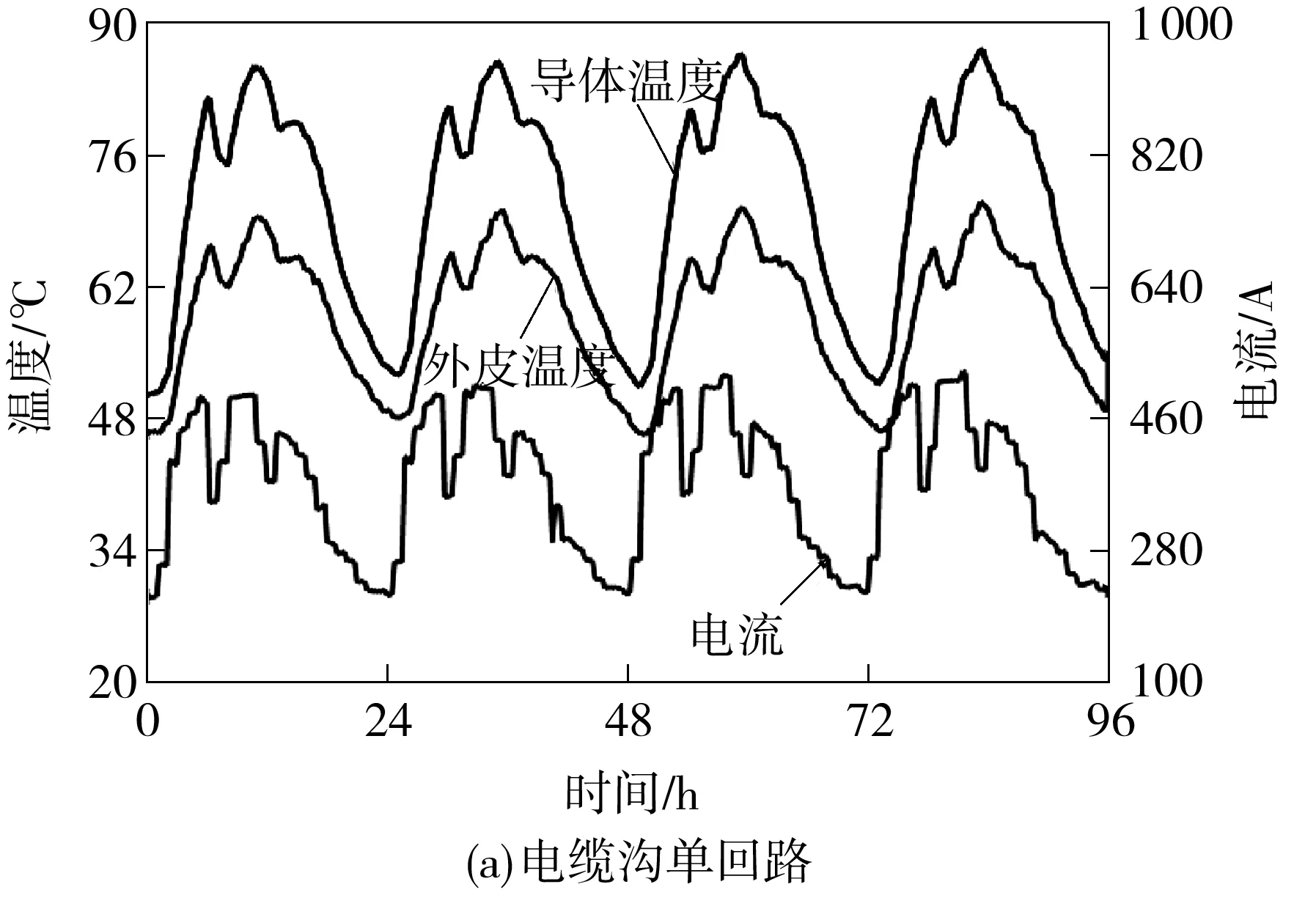
图1　温升试验结果图

从图1可以看出，在整个试验过程中，电缆导体温度和外皮温度、电流有很强的相关性，三者的变化趋势基本一致.因此可以根据测量的电缆外皮温度和加载的电流来计算电缆暂态导体温度.

3基于PSO-SVM的电缆暂态导体温度计算模型训练

3.1参数设置

从图1可知，三芯电缆导体温度滞后电流约1.25 h，因此文中以t-5Δt，t-4Δt，t-3Δt，t-2Δt，t-Δt共5个时刻的电流和外皮温度作为模型的输入，电缆t时刻导体温度作为模型的输出.

文中选择电缆沟敷设温升试验的75个小时(共300组)数据作为训练样本构建暂态导体温度支持向量机模型，并设定训练样本均方误差eMSE的阈值为10-3，最大迭代次数Nmax=100，种群的粒子数m=20，学习因子c1=c2=2，C的范围为[0,200],粒子在代表C的空间的速度区间为[-60,60]，γ范围为[0,1]，粒子在代表γ的空间的速度区间为[-0.6,0.6].

PSO算法的速度更新公式中的惯性权重系数ω决定了粒子先前速度对当前速度的影响程度，从而起到平衡算法全局搜索和局部搜索能力的作用[26].在迭代开始阶段，ω取值较大可以使算法不容易陷入局部最优；迭代末期，ω取值较小可以增强粒子局部搜索能力，加快收敛速度.文中ω设置为随迭代次数增加而减小的函数：

ω(t)=ωmin+(ωmax-ωmin)(Nmax-N)/Nmax

(12)

式中，N为当前迭代数，Nmax为最大迭代次数，惯性权重系数最大值ωmax=0.8，最小值ωmin=0.5.

当在某次迭代中出现适应度值小于10-3的粒子或者迭代次数达到Nmax时，退出粒子群算法.

3.2模型性能评价指标

为更直观地展示所建立模型的性能，采用均方误差(RMSE)、平均绝对误差(MAE)以及平均相对误差(MAPE)来评价模型的计算精度.RMSE、MAE以及MAPE由如下表达式定义：

(13)

3.3模型训练结果

文中基于训练样本、采用粒子群算法得到的最优训练参数为c=111.71和γ=0.010.粒子群算法的eMSE曲线见图2.由图2可见，eMSE在第11代趋于稳定，此时适应度值2.85×10-3，训练结果见图3，训练样本误差用式(13)来表示.

均方误差、平均绝对误差、平均相对误差分别为0.60 ℃、0.48 ℃、0.74%，因而PSO-SVM模型有较好的拟合能力，能够准确地反映导体温度与外皮温度及电流的非线性关系.

图2　适应度曲线

图3　训练样本计算结果

4模型计算性能的分析

4.1不同算法对比及分析

为体现文中建立的模型在计算精度的优越性，分别采用BP神经网络[10]、热路模型[6]和PSO-SVM模型对电缆沟敷设温升试验的48组数据(与训练样本数据不存在交集)进行计算.BP神经网络的训练样本与文中PSO-SVM模型训练样本一致；热路模型的热阻、热容、损耗均采用IEC推荐公式计算；3种模型的计算结果见图4，计算误差如表2所示.

图4　不同模型下的计算值与实测值比较

Fig.4Contrast of the measured and calculated values of diffe-rent models

表2　不同模型下的计算误差

从图4和表2可以看出，相对于热路模型和BP神经网络模型，PSO-SVM模型的计算结果与实测值吻合性更好，PSO-SVM模型的均方误差、平均绝对误差、平均相对误差均小于热路模型和BP神经网络的对应误差值.这主要是因为热路模型的计算准确度受到电缆本体各层传热参数及外部环境参数的影响较大，一方面计算所用参数与实际可能存在较大差别，另一方面一些参数会随温度而变化，若将这些参数简单的考虑为常数则容易产生较大的计算误差；BP神经网络模型过于追求训练误差的最小，导致模型对训练样本以外的测试样本的误差反而增大，即出现所谓的“过拟合”现象，同时，BP神经网络初始神经元之间的权值和阈值一般随机选择，容易陷入局部最小值点.而基于粒子群优化的支持向量机模型采用结构最小化原则，可以在保证计算精度的同时最大限度地克服“过拟合”问题，此外，粒子群算法的引入能够很好地避免模型陷入局部最小值.

4.2模型的泛化能力

为检验基于电缆沟敷设单回路温升试验训练样本得到的模型是否适用于其他环境下电缆暂态导体温度计算，选择排管敷设六回路试验6×240组数据对该模型的泛化能力进行检验.其中温度最高的回路(回路4)计算值和实测值对比如图5所示，各回路误差结果如表3所示.

图5　排管敷设6回路下计算值与实测值比较

Fig.5Contrast of measured valued and calculated valuetof six-circuit cables laid in pipes

表3排管敷设6回路下导体温度计算误差

Table 3Calculation error of conductor temperature of six-circuit cables laid in pipes

回路数RMSE/℃MAE/℃MAPE/%10.750.540.7720.710.500.7230.820.530.8040.780.530.7550.770.520.7560.840.580.83平均值0.780.530.77

从图5及表3可以看出：虽然检验样本与训练样本试验环境差异很大，但排管敷设六回路电缆暂态导体温度计算值曲线几乎逼近导体温度的实测值曲线；排管敷设六回路的均方误差、平均绝对误差、平均相对误差平均值分别为0.78 ℃，0.53 ℃，0.77%.对比表2和3可以看出，用电缆沟敷设单回路样本训练得到的模型用于排管敷设六回路的导体温度计算时，误差并没有明显上升，表明文中所建模型有很强的泛化能力.

5结论

文中引入粒子群算法对支持向量机中的惩罚因子和核参数进行寻优，建立电缆暂态导体温度计算的PSO-SVM模型；以三芯电缆为例，计算电缆导体暂态温度，并与电缆温升试验结果进行比较，以验证模型计算的准确性；将该模型与热路模型、BP神经网络的计算结果进行比较，以比较不同算法的精度；将电缆沟敷设单回路的试验数据训练的模型应用于排管敷设6回路电缆暂态导体温度计算，以验证模型的泛化能力.通过上述研究，文中得到以下结论：

1)基于粒子群优化的支持向量机的计算模型可以准确计算电缆暂态导体温度.

2) 该PSO-SVM计算模型以电缆导体电流和外皮温度作为输入参数，以电缆暂态导体温度作为输出，无需考虑电缆的各层传热参数和敷设环境.

3)电缆温升试验证明该PSO-SVM模型具有较高的计算精度，且其计算误差小于热路模型和BP神经网络模型.

4)PSO-SVM模型具有很强的泛化能力.将电缆沟敷设单回路试验数据训练得到的模型用于排管敷设六回路的导体温度计算时，误差没有明显上升.

参考文献：

[1]梁永春,李延沐.利用模拟热荷法计算地下电缆稳态温度场 [J].中国电机工程学报,2008,28(16):128- 134．

LIANG Yong-chun,LI Yan-mu.Calculation of the static temperature field of underground cables using heat charge simulation method [J].Proceedings of the CSEE,2008,28(16):128- 134．

[2]马国栋.电线电缆载流量 [M].北京：中国电力出版社,2003.

[3]张尧,周鑫,牛海清,等.单芯电缆热时间常数的理论计算与试验研究 [J].高电压技术,2009(11):2801- 2806.

ZHANG Yao,ZHOU Xin,NIU Hai-qing,et al.Theoretical calculation and experimental research on thermal time constant of single-core cables [J].High Voltage Engineering,2009(11):2801- 2806.

[4]梁永春,柴进爱,李彦明,等.基于FEM的直埋电缆载流量与外部环境关系的计算 [J].电工电能新技术,2007,26(4):10- 13.

LIANG Yong-chun,CAI Jin-ai,LI Yan-ming,et al.Calculation of ampacity reduction factors for buried cables with surroundings based on FEM [J].Advanced Technology of Electrical Engineering and Energy,2007,26(4):10- 13.

[5]闫澜锋.10kV 三芯电缆温度场分布特性及导体温度计算的仿真与实验研究 [D].广州:华南理工大学,2012.

[6]周鑫.单芯电力电缆导体温度计算及试验研究 [D].广州:华南理工大学电力学院,2010.

[7]刘毅刚,罗俊华.电缆导体温度实时计算的数学方法 [J].高电压技术,2005,31(5):52- 54.

LIU Yi-gang,LUO Jun-hua.Mathematical method of temperature calculation of power cable conductor in real time [J].High Voltage Engineering,2005,31(5):52- 54.

[8]Olsen R S,Holboll J,Gudmundsdottir U S.Dynamic temperature estimation and real time emergency rating of transmission cables [C]∥Proceedings of Power and Energy Society General Meeting.[S.l.]:IEEE,2012:1- 8.

[9]郑雁翎,仪涛,张冠军,等.分散式排管敷设电缆群温度场的流固耦合计算 [J].高电压技术,2010,36(6):1566- 1571.

ZHENG Yan-ling,YI tao,ZHANG Guan-jun,et al.Fluid-solid coupling computation on temperature field of decentralized pipe cable system [J].High Voltage Enginee-ring,2010,36(6):1566- 1571.

[10]雷成华,刘刚,李钦豪.BP 神经网络模型用于单芯电缆导体温度的动态计算 [J].高电压技术,2011,37(1):184- 189.

LEI Cheng-hua,LIU Gang,LI Qin-hao.Dynamic calculation of conductor temperature of single-cable using BP neural network [J].High Voltage Engineering,2011,37(1):184- 189.

[11]Vapnik V.The nature of statistical learning theory [M].[S.l.]:Springer Science & Business Media,2013.

[12]邓乃扬,田英杰.支持向量机——理论、算法与扩展 [M].北京:科学出版社,2009.

[13]李国政,王猛,曾华军.支持向量机导论 [M].北京:电子工业出版社,2004.

[14]张学工.关于统计学习理论与支持向量机 [J].自动化学报,2000,26(1):32- 42.

ZHANG Xue-gong.Introduction to statistical learning theory and support vector machines [J].Acta Automatic Sinica,2000,26(1):32- 42.

[15]邓万宇,郑庆华,陈琳,等.神经网络极速学习方法研究 [J].计算机学报,2010,33(2):279- 287.

Deng Wan-yu，Zheng Qing-hua，Chen Lin，et al．Research on extreme learning of neural networks [J]．Chinese Journal of Computers，2010,33(2)：279- 287.

[16]许建华,张学工,李衍达.支持向量机的新发展 [J].控制与决策,2004,19(5):481- 484.

XU Jian-hua,ZHANG Xue-gong,LI Yan-da.Advances in support vector machines [J].Control and Decision,2004,19(5):481- 484.

[17]陈伟根,滕黎,刘军,等.基于遗传优化支持向量机的变压器绕组热点温度预测模型 [J].电工技术学报,2014,29(1):44- 51.

CHEN Wei-gen,TENG Li,LIU Jun,et al.Transformer winding hot-spot temperature prediction model of support vector machine optimized by genetic algorithm [J].Transactions of China Electrotechnical Society,2014,29(1):44- 51.

[18]戴栋,黄筱婷,代洲,等.基于支持向量机的输电线路覆冰回归模型 [J].高电压技术,2013,39(11):2822- 2828.

DAI Dong,HUANG Xiao-ting,DAI Zhou,et al.Regre-ssion model for transmission lines icing based on support vector machine [J].High Voltage Engineering,2013,39(11):2822- 2828.

[19]鞠鲁峰,王群京,李国丽,等.永磁球形电机的支持向量机模型的参数寻优 [J].电工技术学报,2014,29(1):85- 90.

JU Lu-feng,WANG Qun-jing,LI Guo-li,et al.Parameter optimization for support vector machine model of permanent magnet spherical motors [J].Transactions of China Electrotechnical Society,2014,29(1):85- 90.

[20]李晓宇,张新峰,沈兰荪.一种确定径向基核函数参数的方法 [J].电子学报,2006,33(B12):2459- 2463.

LI Xiao-yu,ZHANG Xin-feng,SHEN Lan-sun.A selection means on the parameter of radius basis function [J].Acta Electronica Sinica,2005,33(B12):2459- 2463.

[21]温玉锋.材料实验数据的支持向量回归分析及应用 [D].重庆:重庆大学数理学院,2009.

[22]FEI S,WANG M J,MIAO Y,et al.Particle swarm optimization-based support vector machine for forecasting dissolved gases content in power transformer oil [J].Energy Conversion and Management,2009,50(6):1604- 1609.

[23]DEL Valle Y,VENAYAGAMOORTHY G K,MOHAGH-

EGHI S,et al.Particle swarm optimization:basic concepts,variants and applications in power systems [J].IEEE Transactions on,Evolutionary Computation,2008,12(2):171- 195.

[24]宋风忠.基于粒子群算法风力发电系统风速预测研究 [J].电气应用,2011,24:024.

SONG Feng-zhong.Wind speed prediction research of wind power generation system based on particle swarm optimization [J].Electrotechnical Application,2011,24:024.

[25]徐刚,瞿金平,杨智韬.一种改进的自适应粒子群优化算法 [J].华南理工大学学报(自然科学版),2008,36(9):6- 10.

XU Gang,QU Jin-ping,YANG Zhi-tao.An improved adaptive particle swarm optimization algorithm. [J] Journal of South China University of Technology(Natural Science Edition),2008,36(9):6- 10.

[26]吴杰康,熊焰.风水气互补发电优化的云模型自适应粒子群优化算法 [J].中国电机工程学报,2014,34(增刊):17- 24.

WU Jie-kang,XIONG Yan.An cloud model theory based adaptive particle swarm optimization algorithm for complementary power generation optimization of wind-energy,hydro-energy and natural gas [J].Proceedings of the CSEE,2014,34(Suppl):17- 24.

Calculation of Cable Temperature Based on Support Vector Machine Optimized by Particle Swarm Algorithm

NIUHai-qing1YEKai-fa1XUJia1WUJu-zhuo1LUOJian-bin2LUGuo-jun2

(1.School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China;2.Tests and Research Institute of Guangzhou Power Supply Bureau Co.,Ltd., Guangzhou 510410,Guangdong, China)

Abstract:Cable conductor temperature is a main factor affectingthe life and material utilization of the cable, and is an important parameter reflecting cable's operation state. However, it is difficult to directly measure the conductor temperature of in-use cables, so that a temperature calculation is necessary. In this paper, a model to calculate the transient temperature of cable conductor based on the support vector machine(SVM) is proposed. In this model, both the load current and the skin temperature are used as the inputs and the conductor temperature is taken as the output. Moreover, in order to improve the calculation accuracy and avoid blind selection of training parameters, the particle swarm optimization (PSO)algorithmis introduced in the model for optimizing the punishment index C and the core parameter γ. In addition, a comparison between the simulated and the experimental results is made, finding that the proposed PSO-SVM model is superior to the thermal circuit model and the BP neural network because it helps to obtain more accurate transient temperature and possesses good generalization ability.

Key words:cable;conductor temperature; support vector machine; particle swarm optimization; transient calculation

收稿日期:2015- 09- 11

*基金项目:国家高技术研究发展计划(863计划)项目(2015AA050201)

Foundation item:Supported by the National High Technology Research and Development of China(863Program)

作者简介:牛海清(1969-)，女，博士，副教授，主要从事高压输电线路及高压电气设备等的研究.E-mail:niuhq@scut.edu.cn

文章编号:1000- 565X(2016)04- 0077- 07

中图分类号：TM 726.4

doi：10.3969/j.issn.1000-565X.2016.04.012