基于相空间重构和RELM的短时交通流量预测*

商强　杨兆升,2,3†　李志林　李霖　曲鑫

(1.吉林大学 交通学院， 吉林 长春 130022； 2.吉林大学 汽车仿真与控制国家重点实验室， 吉林 长春 130022；

3.吉林大学 吉林省道路交通重点实验室， 吉林 长春 130022)

基于相空间重构和RELM的短时交通流量预测*

商强1杨兆升1,2,3†李志林1李霖1曲鑫1

(1.吉林大学 交通学院， 吉林 长春 130022； 2.吉林大学 汽车仿真与控制国家重点实验室， 吉林 长春 130022；

3.吉林大学 吉林省道路交通重点实验室， 吉林 长春 130022)

摘要:为了提高短时交通流量预测的精度，构建了基于相空间重构和正则化极端学习机的短时交通流量预测模型.首先采用C-C算法求解交通流量时间序列的最佳时间延迟和嵌入维数，进行相空间重构；然后选用G-P算法计算序列关联维数，判断出短时交通流量序列具有混沌特性.在此基础上，将重构数据作为正则化极端学习机的输入和输出来训练模型，并采用网格搜索法优化模型参数.最后以实测数据为基础，对模型的预测效果进行对比分析.结果表明，新构建模型的预测效果良好，能够有效提高短时交通流量预测精度.

关键词：交通工程；短时交通预测；相空间方法；极端学习机

实时准确的交通流量预测是智能交通控制和诱导的前提.交通控制的最大周期一般为2.5～3.0 min,交通诱导的周期一般为5 min，因此，5 min内的短时交通流预测已成为研究热点.短时交通流量预测模型和方法大致分为3类：①经典数理方法模型，如卡尔曼滤波、非参数回归模型[1- 3]；②人工智能模型，如神经网络、支持向量机[4- 6]；③非线性系统理论方法，如小波分析、混沌理论[7- 8].其中，混沌理论、神经网络和支持向量机在分析复杂的、不确定的非线性系统方面有较大优势.然而传统神经网络模型采用梯度下降学习算法，存在学习速度慢、易陷入局部最优的问题.极端学习机(ELM)是一种新发展的神经网络学习方法，能够克服传统神经网络的缺陷，提升训练速度[9- 10].为改善ELM 的泛化能力，减少过拟合现象，与支持向量机类似，借鉴统计学习理论中的结构风险最小化原理，提出了正则化极端学习机(RELM)，并且在预测和模式识别中得到应用[11- 12].短时交通流自身的非线性、随机性和不确定性等特征，在很大程度上增加了预测的难度.经典数理方法模型通常预先给定模型结构和诸多假设(如残差服从正态分布、交通流时间序列平稳)，难以取得满意的预测效果.RELM模型没有预先给定模型结构，而是以实际数据为驱动，并且具有较高的训练速度和良好的泛化能力.

有鉴于此，文中提出一种将混沌理论中的相空间重构(PSR)与RELM相结合的短时交通流量预测模型(PSR-RELM)，并通过实测数据对模型预测效果进行了对比验证.

1相空间重构

相空间重构是分析混沌时间序列的前提和基础，能够将一维时间序列转化到多维相空间，把混沌时间序列预测问题转化为相空间的短期演化问题，从而合理地确定模型的输入和输出，有利于提高模型预测的精度.根据Takens嵌入延时定理[13]，如果嵌入维数m和时间延迟选择恰当，则重构相空间与原系统等价，具有相同的拓扑结构.

设长度为N的一维交通流量时间序列为：x={xi|i=1,2,…,N}，那么重构后的相空间为

(1)

其中，M=N-(m-1)为相点数.在重构相空间中，每个相点包括m个元素，每两个相邻元素的间隔为.

嵌入维数m和时间延迟的选取决定了相空间重构的质量.传统观点认为m和是相互独立的，需要单独或依次求解，近年研究表明m和有着密切关系，可通过延迟时间窗w=(m-1)建立两参数之间的关系.C-C算法[14]使用关联积分构成统计量，通过统计量和时间延迟的关系同时求得和w，进而得到嵌入维数，关联积分定义如下：

(2)

式中：M为相点数；r为邻域半径；dij为相空间中两点间的欧氏距离，dij=‖Xi-Xj‖；H(z)为Heaviside阶跃函数，其定义为

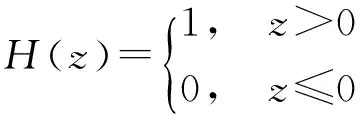
(3)

将时间序列{x(t),t=1,2,…,N}划分为t个不相交的子序列.对于每个子序列，有

(4)

对全部S(m,N,r,t)取平均值：

(5)

式中，M为嵌入维数，J为r的数目.定义ΔS(m,t)为关于r的最大偏差，则

ΔS(m,t)=max{S(m,rj,t)}-min{S(m,rj,t)}

(6)

根据文献[15]中有关几种重要渐进分布的统计结论，在实际中常取m=2,3,4,5，ri=iσ/2,i=1,2,3,4,其中σ为序列的标准差.分别计算以下3个统计量：

(7)

(8)

(9)

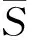
2交通流混沌特性分析

交通流量时间序列具有混沌特性，是采用相空间重构方法构建预测模型的前提.吸引子关联维数是判断序列是否具有混沌特性的重要指标.对于随机序列，关联维数随着嵌入维数的增加而增大，不会达到饱和；而对于混沌序列，关联维数随着嵌入维数的增加而逐渐趋于饱和.G-P算法是计算关联维数的常用方法，其计算步骤如下[16]：

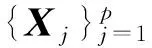
(10)

对所有的Xi(i=1,2,…,p)重复这一过程，得到关联积分函数:

(11)

式中,θ(u)={1,u≥0;或0,u<0}，r为无标度观测尺度.当r充分小时,式(11)逼近下式：

lnCm(r)=lnC+D(m)lnr

(12)

则相空间Rm中奇异吸引子的关联维数D可表示为

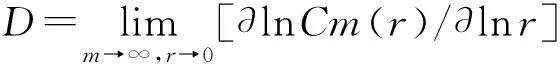
(13)

3基于RELM的预测模型

3.1RELM基本原理

RELM基本原理如下：对于时间序列集合:G={(x1,t1),…,(xi,ti),…,(xN,tN)}.其中，xi=[xi1,…,xin]∈Rn，ti=[ti1,ti2,…,tim]∈Rm，i=1,2,…,n，隐含层节点数为L，激励函数为g(x)的RELM回归模型为

(14)

Hβ=T

(15)

式中，H为隐含层输入矩阵，具体形式为

RELM模型求解优化问题如下：

(16)

s.t.

(17)

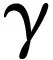
译文： Third，starting from childhood means that children need to start with themselves，and make every possible effort to cultivate good morality．“A young idler，an old beggar．” and “A journey of one thousand miles begins with the first step．”[1]203

(18)

式中，ω=[ω1,ω2,…,ωN]，表示Lagrange乘子.分别求参数偏导，令Lagrange函数偏导数为0，解得

(19)

式中，I为单位矩阵.最后得到RELM预测模型为

(20)

3.2RELM模型输入和输出

为了提高RELM模型的预测精度，将模型设计为单步预测模型，即模型的输入为重构相空间的一个相点：Xi=[xi,xi+,…,xi+(m-1)]T，i=1,2,…,M,模型输出为下一时刻i+(m-1)+1的交通流量xi+(m-1)+1.

为了消除原始数据形式不同带来的影响，提升模型训练速度和预测性能，在模型训练和测试前，需要将输入和输出样本归一化到区间[0,1]，其公式为

(21)

式中，xi为原始数据，yi为归一化数据，xmax为原始数据的最大值，xmin为原始数据的最小值.

4实际应用

实验数据来源于上海快速路布设的感应线圈检测器，能够记录经过检测器的车辆数，每20 s输出一次统计结果.考虑到交通控制周期和交通诱导周期的需求，将20 s间隔交通流量合成为2 min间隔的交通流量.选取连续5个工作日(2008年9月8日至9月12日)6:00-18:00时段内的2 min交通流量序列作为分析对象.所得交通流量时间序列如图1所示，由图可知交通流量变化复杂，表现出非线性、时变性和不确定性.将前4天交通流量数据作为训练集，构建预测模型；将第5天交通流量数据作为测试集，对比分析模型的预测效果.

图1　5天交通流量时间序列

4.1相空间重构

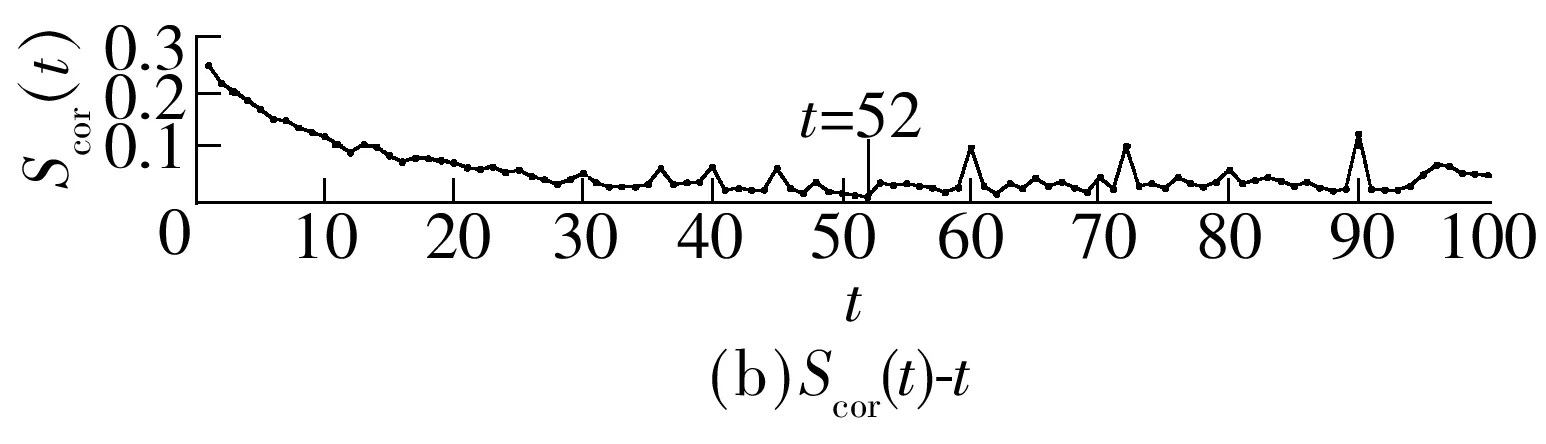
使用C-C算法计算交通流量时间序列的最佳嵌入维数m和最佳时间延迟.(t)与t、Scor(t)与t的关系曲线如图2所示.当t=6时(图中箭头标注位置)，(t)取得第1个极小值，即最佳时间延迟=6.当t=52时(图中箭头标注位置)，Scor(t)取得最小值，即延迟时间窗w=52，从而求得最佳嵌入维数m=10.

4.2交通流混沌特性分析

通过G-P算法求解交通流量序列的饱和关联维数，lnC(r)-lnr关系曲线如图3所示.由图可见，lnC(r)-lnr曲线随嵌入维数m增大逐渐平行，即关联维数逐渐达到饱和.拟合m=15时，lnC(r)-lnr关系曲线的近似直线部分.所得拟合直线斜率为2.807 2，可认为交通流量序列的吸引子饱和关联维数D=2.807 2.随着嵌入维数的增加，关联维数逐渐趋于饱和.这一现象说明2 min采样间隔的交通流量时间序列具有混沌特性.

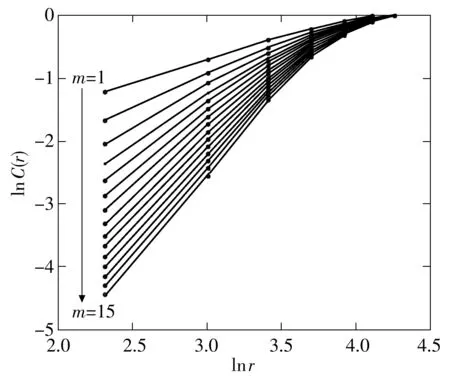
图3　交通流量时间序列的ln C(r)-ln r曲线

4.3模型训练和参数优化

前4个工作日的交通流量时间序列包括1 440个数据，其重构相空间为

(22)

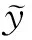
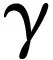
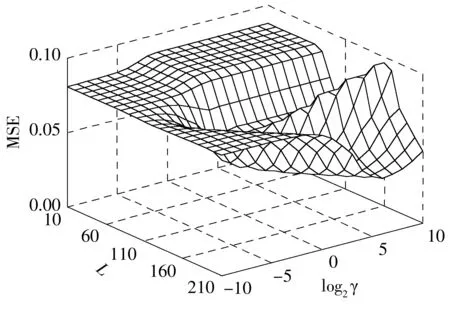
图4　网格搜索RELM的最优参数组合

4.4模型预测性能分析

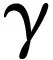
为了更加精确地评价各模型预测效果，除了式(22)给出的MSE指标，再引入平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均等系数(EC)3个评价指标，评价各个模型的预测效果.

(1)平均绝对误差(MAE)

(23)

(2)平均相对百分比误差(MAPE)

(24)

(3)均等系数(EC)

(25)

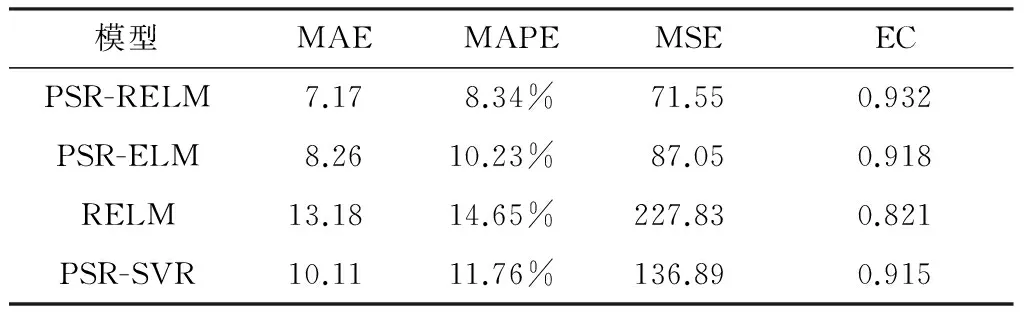
使用第5天交通流量(包括360个2 min交通流量数据)构建测试集.图5为各模型交通流量预测值和实际值的对比曲线.表1为各模型预测的4个指标值.由图5可知，PSR-RELM模型预测流量与实际流量的拟合效果最好.从6:20至7:30，交通流量在波动中迅速增加，早高峰出现.交通流量的急剧变化增大了预测难度.从图5给出的各模型预测效果曲线可以看出，在该时段内PSR-RELM模型拟合效果同样超过其他预测模型.由表1可知，PSR-RELM模型EC值为0.932，比其他模型EC值更加接近1，也说明该模型预测值与实际值拟合最佳.在3个误差指标(MAE、MAPE和MSE)方面，PSR-RELM模型预测误差均低于其他模型，表明该模型具有更高的预测精度.其中，未经相空间重构的RELM模型预测效果最差(EC值低于0.9，3项误差指标均大于其他预测模型)，说明合理的相空间重构能够有效提高交通流量混沌时间序列的预测精度.综上所述，文中构建的短时交通流量预测模型(PSR-RLEM)预测效果良好，能够进一步提高短时交通流量预测精度.

图5　不同模型预测结果

Table 1Comparison of prediction results based on multiple evaluation indexes

模型MAEMAPEMSEECPSR-RELM7.178.34%71.550.932PSR-ELM8.2610.23%87.050.918RELM13.1814.65%227.830.821PSR-SVR10.1111.76%136.890.915

5结论

文中提出了一种基于相空间重构和RELM的短时交通流量预测模型(PSR-RELM).将交通流量时间序列进行相空间重构，并通过关联维数逐渐趋于饱和，判定原序列具有混沌特性；根据重构相空间的相点确定RELM输入-输出，采用网格搜索法优化模型参数，完成模型的构建.基于相同的实测数据，将新建模型与PSR-ELM模型、RELM模型、PSR-SVR模型的预测效果进行多指标对比，得出以下结论：

(1)基于相空间重构与正则化极端学习机的预测模型(PSR-RELM)具有最佳的预测效果，预测精度优于基于相空间重构与极端学习机的预测模型(PSR-ELM)、基于相空间重构和支持向量回归的预测模型(PSR-SVR)、未经相空间重构的正则化极端学习机预测模型(RELM).

2)未经相空间重构的极端学习机模型(RELM)预测性能均低于其他经过相空间重构的预测模型(PSR-RELM、PSR-ELM、PSR-SVR)，说明相空间重构能够提高混沌交通流量时间序列的预测精度.

参考文献：

[1]WANG Y,PAPAGEORGIOU M.Real-time freeway traffic state estimation based on extended Kalman filter:a gene-ral approach [J].Transportation Research Part B:Metho-dological,2005,39(2):141- 167.

[2]赵建东,王浩,刘文辉.高速公路旅行时间的自适应插值卡尔曼滤波预测 [J].华南理工大学学报(自然科学版),2014,42(2):109- 115.

ZHAO Jian-dong,WANG Hao,LIU Wen-hui.Prediction of expressway travel time based on adaptive interpolation kalman filtering [J].Journal of South China University of Technology(Natural Science Edition),2014,42(2):109- 115.[3]张晓利，陆化普.非参数回归方法在短时交通流预测中的应用 [J]．清华大学学报(自然科学版)，2009,49(9):1471- 1475.

ZHANG Xiao-li,LU Hua-pu.Non-parametric regression and application for short-term traffic flow forecasting [J].Journal of Tsinghua University(Science and Technology),2009,49(9):1471- 1475.

[4]HONG W C,DONG Y C,ZHENG F F,et al.Forecasting urban traffic flow by SVR with continuous ACO [J].Applied Mathematical Modelling,2011,35(3):1282- 1291.

[5]杨兆升,王媛,管青.基于支持向量机方法的短时交通流量预测方法 [J].吉林大学学报(工学版),2006,36(6):881- 884.

YANG Zhao-sheng,WANG Yuan,GUAN Qing.Short-time traffic prediction method based on SVM [J].Journal of Jilin University(Engineering and Technology Edition),2006,36(6):881- 884.

[6]傅贵,韩国强,逯峰,等.基于支持向量机回归的短时交通流预测模型 [J].华南理工大学学报(自然科学版),2013,41(9):71- 76.

FU Gui,HAN Guo-qiang,LU Feng,et al.Short-term traffic flow forecasting model based on support vector machine regression [J].Journal of South China University of Technology(Natural Science Edition),2013,41(9):71- 76.

[7]张玉梅，曲仕茹，温凯歌．交通流量的混沌特性分析及预测模型研究 [J].土木工程学报，2009，42(1):119- 123.

ZHANG Yu-mei,QU Shi-ru,WEN Kai-ge.Chaotic pro-perty analysis and prediction model study for traffic flow time series [J].China Civil Engineering Journal,2009,42(1):119- 123.

[8]杨立才,贾磊,孔庆杰,等.粗正交小波网络及其在交通流预测中的应用 [J].系统工程理论与实践,2005,25(8):124- 129.

YANG Li-cai,JIA Lei,KONG Qing-jie,et al.Rough orthogonal wavelet network and its applications to the traffic flow forecast [J].Systems Engineering-Theory & Practice,2005,25(8):124- 129.

[9]HUANG G B,ZHU Q Y,SIEW C K.Extreme learning machine:theory and applications [J].Neurocomputing,2006,70(1):489- 501.

[10]SINGH R,BALASUNDARAM S.Application of extreme learning machine method for time series analysis [J].International Journal of Intelligent Technology,2007,2(4):256- 262.

[11]邓万宇，郑庆华，陈琳，等．神经网络极速学习方法研究 [J].计算机学报，2010,33(2):279- 287.

DENG Wan-yu,ZHENG Qing-hua,CHEN Lin,et al.Research on extreme learning of neural networks [J].Chinese Journal of Computers,2010,33(2):279- 287.

[12]ZHENG W,QIAN Y,LU H.Text categorization based on regularization extreme learning machine [J].Neural Computing and Applications,2013,22(3/4):447- 456.

[13]TAKENS F.On the numerical determination of the dimension of an attractor [M].Berlin:Spring-Verlag,1985:366- 381.

[14]KIM H S,EYKHOLT R,SALAS J D.Nonlinear dynamics,delay times,and embedding windows [J].Physica D:Nonlinear Phenomena,1999,127(1):48- 60.

[15]BROCK W A,HSIEH D A,LEBARON B D.Nonlinear dynamics,chaos,and instability:statistical theory and economic evidence [M].Cambridge:MIT press,1991.

[16]GRASSBERGER P,PROCACCIA I.Characterization of strange attractors [J].Physical Review Letters,1983,50(5):346.

Short-Term Traffic Flow Prediction Based on Phase Space Reconstruction and RELM

SHANGQiang1YANGZhao-sheng1,2,3LIZhi-lin1LILin1QUXin1

(1.College of Transportation,Jilin University,Changchun 130022, Jilin, China;2.State Key Laboratory of Automobile Simulation and Control, Jilin University,Changchun 130022,Jilin,China;3.Jilin Province Key Laboratory of Road Traffic,Jilin University, Changchun 130022,Jilin,China)

Abstract:In order to increase the accuracy of short-time traffic flow prediction, a flow prediction model based on the phase space reconstruction and the regularized extreme learning machine is put forward. In this method, the C-C method is used to calculate the best time delay and embedding dimension of traffic flow time series for phase space reconstruction,and the G-P algorithm is used to calculate the correlative dimension of the seriesthat is an important judgment index ofthe chaotic characteristics of traffic flow series. Then, the reconstructed phase point data are taken as the inputs and outputsto trainthe regularized extreme learning machine model, and the main parameters of the model are determined by means of grid searching. Finally, a comparative analysis is carried out based on the actual measured traffic flow data. The results show that the proposed model possesses high performance and is effective in improving the accuracy of short-time traffic flow prediction.

Key words:trafficengineering; short-term traffic prediction; phase space method; extreme learning machine

收稿日期:2015- 06- 17

*基金项目:国家科技支撑计划项目(2014BAG03B03)；国家自然科学基金资助项目(51308249,51308248,51408257)；山东省省管企业科技创新项目(20122150251- 5)

Foundation items: Supported by the National Key Technology Reserch and Development Program the Ministry of Science and Technology of China(2014BAG03B03) and the National Natural Science Foundation of China(51308249,51308248,51408257)

作者简介:商强(1987-)，男，博士生，主要从事智能交通信息处理与应用研究.E-mail:shangqiang14@mails.jlu.edu.cn †通信作者: 杨兆升(1938-)，男，教授，博士生导师，主要从事智能交通系统关键理论与技术研究.E-mail:yangzs@jlu.edu.cn

文章编号:1000- 565X(2016)04- 0109- 06

中图分类号：U 491

doi：10.3969/j.issn.1000-565X.2016.04.016