基于局部切空间排列与WSVM的滚动轴承故障诊断*
2016-07-04陈法法肖文荣钟先友
陈法法,李 冕,肖文荣,钟先友
(三峡大学 a.新能源微电网湖北省协同创新中心;b.水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002)
基于局部切空间排列与WSVM的滚动轴承故障诊断*
陈法法a,b,李冕b,肖文荣b,钟先友b
(三峡大学 a.新能源微电网湖北省协同创新中心;b.水电机械设备设计与维护湖北省重点实验室,湖北 宜昌443002)
摘要:针对滚动轴承的多类故障特征非线性难以有效辨识的问题,提出基于局部切空间排列和小波支持向量机的滚动轴承故障诊断方法。在由集成经验模式分解(Ensemble Empirical Mode Decomposition,EEMD)处理后的频带能量组成的故障特征集中,首先采用局部切空间排列进行约简降维,提取其中的低维敏感特征,随后将获取的低维敏感特征输入给小波支持向量机进行滚动轴承的多类故障辨识。实验结果表明,基于局部切空间排列(local tangent space arrangement,LTSA)和小波支持向量机(wavelet support vector machine,WSVM)的滚动轴承故障诊断方法能够有效提取多类故障的低维敏感特征,并且相对传统诊断方法而言故障诊断精度更高。
关键词:局部切空间排列;小波支持向量机;滚动轴承;故障诊断
0引言
滚动轴承是旋转机械中起动力支撑作用的关键部件,一旦出现故障将严重影响设备的正常运行[1]。建立滚动轴承故障诊断系统来监测和定位故障,可以有效提高旋转机械的运行可靠性。
在滚动轴承的故障诊断过程,从时频域提取故障特征构造故障特征集可以扩大信息量,使得诊断结果更为准确[2-3]。然而,由于时频域特征集中的故障信息往往并不是孤立的,它们往往存在一定的关联,或依赖、或重叠,从而导致故障特征集中存在大量冗余信息,大大增加了故障诊断的复杂度[4]。依据故障特征之间的关联特点,采用非线性流形学习方法—局部切空间排列(local tangent space alignment,LTSA)进行优化融合,可以剔除大量冗余信息,提高故障特征的敏感性[5-6]。
在获取了滚动轴承的敏感特征之后,则需采用合理的智能诊断方法实现故障的可靠辨识。支持向量机(support vector machine,SVM)作为一种模式识别方法,能够在有限的故障特征信息中挖掘出隐含的故障类别信息,具有比神经网络等传统故障诊断方法更强的泛化推广能力[7]。支持向量机通过核函数将输入特征映射到高维特征空间,从而实现故障样本的线性可分,小波函数作为一种优良的时频分析工具,理论上可以逼近任意函数,为此以小波函数为基础,构造小波核支持向量机(wavelet support vector machine,WSVM)作为智能诊断模型[8-9]。
综上,本文提出基于局部切空间排列与小波核支持向量机的滚动轴承故障诊断方法,首先基于典型的时频信号处理方法—集成经验模式分解(Ensemble Empirical Mode Decomposition,EEMD)构造故障样本特征集,再利用局部切空间排列对故障样本特征集进行约简降维处理,提取其中的敏感特征输入给WSVM实现滚动轴承的智能故障诊断。
1局部切空间排列
LTSA的基本思想是通过无限逼近每一样本点的切空间来构建低维流形的局部几何空间,并利用局部切空间排列得到低维流形的嵌入坐标。在这个过程中,有两个关键步骤:拟合局部坐标和构建全局坐标。
1.1拟合局部坐标
给定一个高维样本数据集X=[x1,x2,…xn],xiRm,对于每个样本点xi,利用欧式距离确定其k个近邻点,以这k个近邻点为元素组成邻域矩阵Xi=[xi1,xi2,…xik],随后在样本点xi的邻域内选择一组正交基向量Qi构成xi的d维切空间,计算邻域Xi中每个样本点xij(j=1,2,…,k)到切空间上的正交投影距离i),其中xij,为邻域数据点xij的均值,Qi取Xi(I-eeT/k)的前d个最大的左奇异向量,其中I是单位矩阵,e是单位向量。则Xi在切空间的坐标矩阵θ=[θ1i,θ2i…,θki],该矩阵是对xi邻域内的局部几何结构信息的最佳逼近。
1.2构建全局坐标
构建全局坐标的目的是为了使各个样本数据点邻域信息的局部坐标进行统一映射,即构建的全局坐标应该反映Xi在切空间的坐标矩阵θ=[θ1i,θ2i…,θki]的局部几何结构。设全局坐标Ti=[Ti1,Ti2,…,Tik]是由样本点xi的局部坐标矩阵θ转换得到,即:
(1)
其中,Li是局部映射转换矩阵,Eij为邻域数据的转换误差,由此局部重构误差矩阵可表示为:
Ei=Ti(1-eeT/k)-Liθij
(2)
为了使重构误差最小,则:
Li=Ti(1-eeT/k)θi+
(3)
Ei=Ti(1-eeT/k)(I-θi+θi)
(4)
式中,θi+是θi的广义逆,设B=SWWTST,S=[S1,S2,…,SN],TSi=Ti,则其权值矩阵为:
W=diag[W1,W2,…,WN]
(5)
且有Wi=(I-eeT/k)(I-θi+θi),满足约束TTT=Id。取B的第2到(d+1)个最小的特征值对应的特征向量组成的矩阵,即为高维数据集X对应的低维全局坐标映射矩阵T。
2小波支持向量机
支持向量机的基本思想是通过一个非线性映射函数将输入空间中的数据映射到高维特征空间中去,然后在高维特征空间中进行分类辨识。
y(x)=wTφ(x)+b
(6)
其中:φ(x)为非线性映射函数,支持向量机通过φ(x)将输入空间中的数据映射到高维特征空间中。w和b分别为权值向量和阈值向量,w和b的求取可归结为如下的二次规划问题:
(7)
约束条件为|yi-

(8)
根据KKT条件,以函数L(w,b,e,α)分别对w,b,e,α求偏导并令其等于0,消除变量w,ek。根据统计学习理论通过变换可以求得α和b,进而得到支持向量机的拟合函数为:
(9)
其中k(xk,x)为支持向量机的核函数,通过该函数可以使原始空间中的数据映射到高维空间中,在高维空间实现数据的线性可分,由于小波核函数理论上可以逼近平方可积空间中的任意非线性函数,因此,采用Morlet小波核函数,构建小波支持向量机实现对齿轮箱故障的分类辨识,其中核函数的表达形式如下:
(10)
3基于LTSA与小波支持向量机的滚动轴承故障诊断模型
在滚动轴承的故障诊断中,构造合理的敏感特征集对故障的可靠诊断十分必要。故障特征提取太多则导致诊断模型运算复杂、收敛速度慢,故障特征提取太少则导致诊断信息不完整,故障诊断精度低。为此采用LTSA从高维特征集中提取出适合于小波支持向量机的低维敏感特征。
基于LTSA与小波支持向量机的滚动轴承故障诊断模型如图1所示,其诊断的具体步骤如下:
(1)特征提取。对滚动轴承的振动故障信号进行预处理,并对预处理后的信号进行EEMD分解,提取分解的IMF分量能量构造高维特征集。
(2)特征降维。采用LTSA流形学习算法对高维特征集进行约简降维处理,获取其中的低维敏感特征集。
(3)参数寻优。为了保证小波支持向量机的优良特性,采用粒子群算法对小波支持向量机的惩罚参数和核函数参数进行优化处理,获取最优的模型参数[10]。
(4)故障诊断。基于低维敏感特征集分别构造训练集和测试集,将训练集输入给参数优化的小波支持向量机进行模型训练,随后利用测试集数据进行故障诊断测试,输出诊断结果。

图1 基于LTSA与WSVM的滚动轴承故障诊断模型
4实例分析
4.1实验设置
滚动轴承的振动故障数据来源于实验室实测的滚动轴承实验数据,测试设备的布置及测试系统如图2所示,实验对象为单级齿轮箱电机输入端的端部轴承,轴承型号为6206-2RS,电机通过输入轴带动主齿轮以710r/min的速度旋转,齿轮箱上的4个端部轴承都经过良好的润滑。

图2 滚动轴承测试装置示意图
在每个轴承上分别安装石英ICP加速度传感器进行振动故障信号的测量,采样频率为10kHz,空载模式实际测试过程中共获取了实验轴承的正常状态、内圈损伤、外圈损伤、混合故障(内圈和外圈同时损伤)共4种运行状态下的振动信号,轴承在不同状态下的振动信号时域波形如图3所示。

图3 滚动轴承不同状态下的时域波形图
从图3可以看出轴承的不同状态其时域波形有一定的区别,但是仅依据此对轴承进行故障诊断不具说服力,需要对滚动轴承的振动状态数据进一步分析确定其定量的特征指标。
4.2故障诊断及结果分析
(1) 特征提取
集成经验模式分解EEMD在传统EMD分解原理的基础上,通过引入高斯白噪声,能够将原始振动信号准确的分解到不同的尺度上[11]。当轴承在不同位置出现故障时,不同尺度上对应振动信号的频率分布和幅值能量均会发生改变[12]。图4为轴承外圈故障的振动信号进行EEMD分解的结果(N=100,白噪声的标准偏差取振动信号标准偏差的0.2倍),通过EEMD分解之后得到了8个IMF分量。从图4可以看出,EEMD把非平稳的轴承故障信号分解成了有限个平稳的IMF分量之和,不同的IMF分量包含了不同的时间尺度。

图4 轴承外圈故障振动信号的 EEMD 分解结果
在此,引入Shannon信息熵来捕获这种变化。轴承在某种故障状态下的振动信号x(t)经过EEMD分解得到了n个IMF,相应的可计算出各自的幅值能量E={E1,E2,…,En},由此可以定义EEMD的能量熵为:

表1 轴承在不同工作状态下的EEMD能量熵
从表1可以看出,轴承在不同运行状态下其对应的EEMD熵值也不同,轴承正常状态时的EEMD熵值要大于轴承故障时的EEMD熵值。由于轴承在正常状态下,其振动信号的能量分布相对平均,当轴承出现外圈故障或内圈故障时,相应的振动信号其对应的特征频带内其幅值特征会明显增强,此时振动信号分布的不确定性减少,熵值增大。当轴承在外圈和内圈同时出现故障时,在各自特征频段内的幅值能量均有聚集,因此,此时的EEMD能量熵最小。由此可以看出,轴承的不同故障在其对应的振动信号经过EEMD分解后的不同尺度上的IMF分量幅值能量会有明显改变。经过实验分析,各状态下的振动信号前8个内禀模态函数分量已经涵盖了原始振动信号的关键特征,为此选取EEMD分解后的前8个内禀模态分量能量特征,将它们综合起来构造滚动轴承故障诊断过程中的故障样本特征集如表2所示,由于篇幅所限,只列举部分样本。
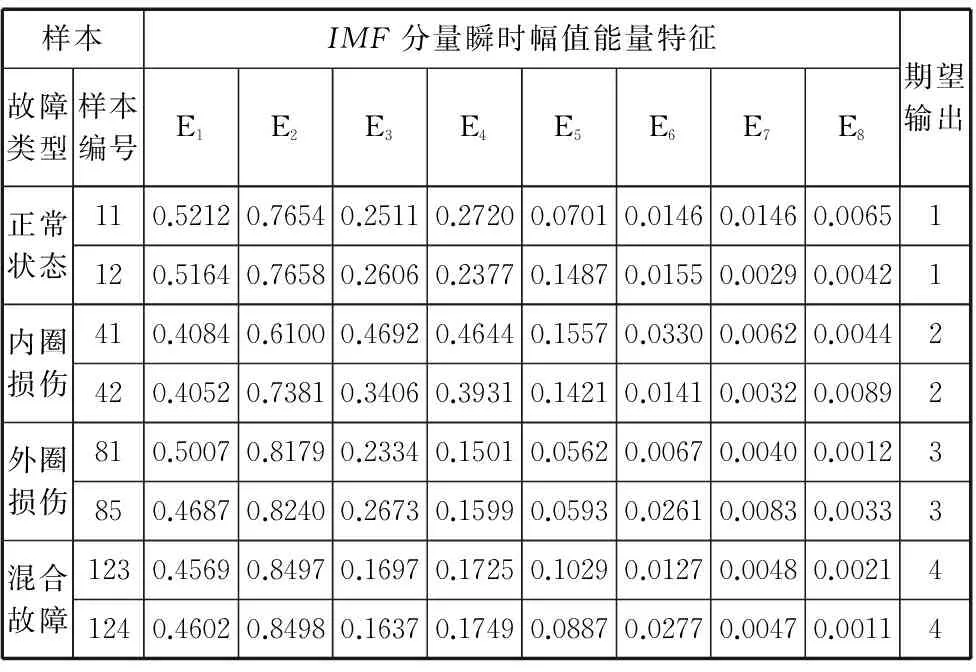
表2 滚动轴承故障诊断特征信息表
(2) 特征约简
针对滚动轴承不同类故障构造的故障样本特征集,分别采用核主成分分析KPCA、等距映射ISOMAP、局部切空间排列LTSA进行约简降维处理,其处理结果如图5所示。
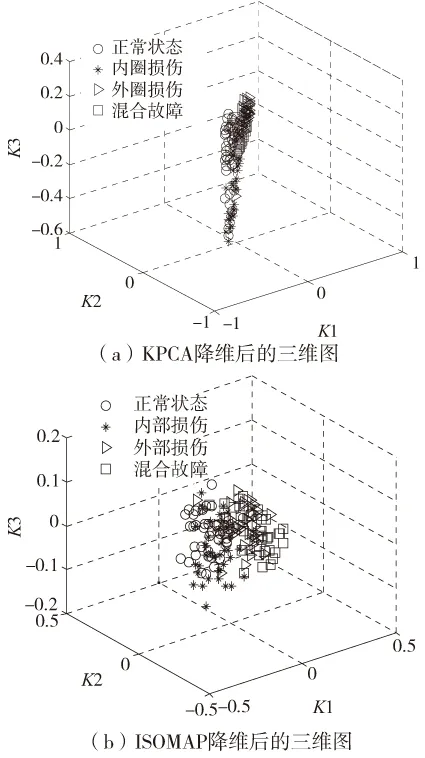

图5 故障特征集在不同降维方法下的投影图
从图5可以看出,三种降维方法对故障样本约简降维之后,均能够将故障样本聚类在一个小的区域内,相比较而言,核主成分分析KPCA对三类故障样本区分度比较弱,各类样本之间存在交叉混叠现象比较严重。同为非线性流形学习的ISOMAP算法和LTSA算法相比较而言,ISOMAP降维后的同类样本之间散度较大,不同类别的故障样本之间的类间距较小,直接导致有效识别不同类故障的难度增大。而通过LTSA降维后不同类故障的低维敏感特征都几乎聚集在一个小的趋于范围内,聚类效果明显优于PCA和ISOMAP,因此,综合比较而言,LTSA算法的约简降维效果最好。
(3) 故障诊断
在得到低维敏感特征之后,则是将该故障特征输入给WSVM实现对滚动轴承故障的智能辨识。为了比较不同核函数对诊断结果的影响,分别采用RBF和小波函数作为核函数对故障样本进行学习,得到相应的SVM模型。惩罚参数值γ和核函数参数值α采用粒子群算法选取,最终确定γ=22.66,α=0.24。
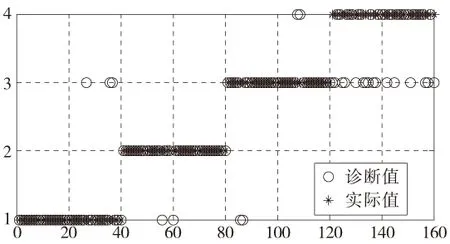
图6 故障样本集在WSVM下的实际诊断效果图
图6是故障样本集在WSVM下的实际诊断效果图,圆圈为WSVM根据输入的低维敏感特征得到的诊断结果显示,星号为故障样本对应的轴承的实际运行状态,WSVM的实际输出1、2、3、4分别对应于轴承的正常状态、内圈损伤、外圈损伤、混合故障。图6中,轴承在不同状态下的样本数量均为40,最终的综合诊断结果为85.56%。通过该种方法可以很好的统计出不同的诊断模型对滚动轴承的故障诊断准确率。不同诊断模型的诊断结果如表3所示。
由表3可以看出,相对于RBF支持向量机,小波核函数支持向量机其诊断精度更高,尤其对轴承混合故障的辨识精度得到很大提高,而参数优化的WSVM其诊断精度又优于随机参数的WSVM,说明参数的合理选择对支持向量机的性能有一定影响,采用粒子群对WSVM进行参数寻优是十分必要的。
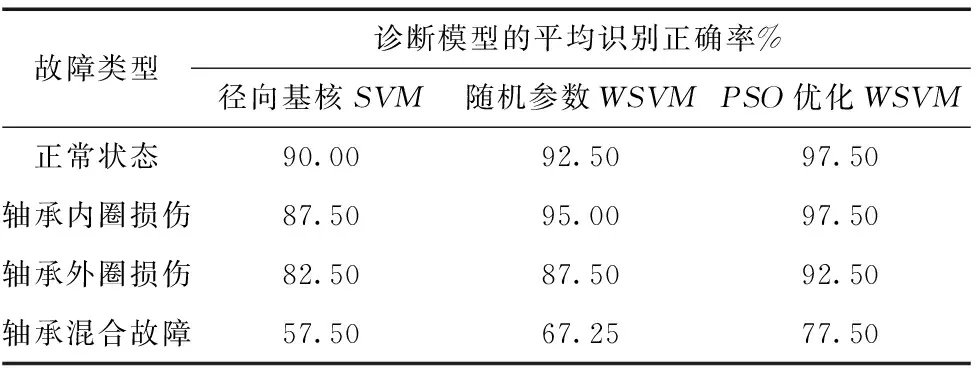
表3 不同模型的故障诊断精度对比
5结论
本文提出的基于局部切空间排列与小波支持向量机的滚动轴承故障诊断模型,通过典型的时频信号分析方法EEMD分解后的IMF分量能量构造故障样本特征集,扩大了特征空间范围,提高了特征信息的完整性。利用LTSA对故障样本特征集进行约简降维处理,提取的低维敏感特征较之传统的约简降维方法其聚类性更强,更加容易实现故障诊断。采用粒子群优化的小波支持向量机能更好的拟合故障特征与故障模式之间的非线性映射关系,从而大大提高滚动轴承的故障诊断精度。
[参考文献]
[1] 任学平,辛向志,庞震,等.基于IMF熵的多传感器网络融合滚动轴承故障诊断方法研究[J].组合机床与自动化加工技术,2015(6):78-82.
[2] 任学平,辛向志,庞震,等.小波包样本熵灰色关联度轴承故障诊断[J].组合机床与自动化加工技术,2015(7):128-130.
[3]ChenFafa,TangBaoping,SongTao.Multi-faultdiagnosisstudyonrollerbearingbasedonmulti-kernelsupportvectormachinewithchaoticparticleswarmoptimization[J].measurement,2014,47(1):576-590.
[4] 董冀媛,穆志纯,欧阳定恒.基于改进的局部切空间排列算法的多姿态人耳识别[J].北京科技大学学报,2010,32(12):1637-1642.
[5] 张熠卓,徐光华,梁霖.基于非线性流形学习的喘振监测技术研究[J].西安交通大学学报,2009,43(7):44-48.
[6] 陈法法,汤宝平,苏祖强.基于局部切空间排列与MSVM的齿轮箱故障诊断[J].振动与冲击,2013,32(5):38-42.
[7]DuyguCalisir,EsinDogantekin.AnautomaticdiabetesdiagnosissystembasedonLDA-WaveletSupportVectorMachineClassifier[J].ExpertSystemswithApplications,2011,38(7):8311-8315.
[8] 汪洪桥.孙富春,蔡艳宁,等.多核学习方法[J].自动化学报,2010,36(8):1037-1050.
[9]郭创新,朱承治,张琳,等.应用多分类多核学习支持向量机的变压器故障诊断方法[J].中国电机工程学报,2010,30(13):128-133.
[10]JZWang,SLZhu,WGZhao,etal,Optimalparametersestimationandinputsubsetforgreymodelbasedonchaoticparticleswarmoptimizationalgorithm[J].ExpertSystemswithApplications, 2011,38(7):8151-8158.
[11] 张敏,崔海龙,陈曦晖,等.基于IMF能量矩和HSMM模型的滚动轴承故障诊断方法[J].组合机床与自动化加工技术,2015(10):101-103.
[12] 张超,陈建军,郭迅.基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J].中南大学学报(自然科学版),2012,43(3):932-939.
(编辑赵蓉)
The Roller Bearing Fault Diagnosis Based on Local Tangent Space Alignment and WSVM
CHEN Fa-faa,b,LI Mianb,XIAO Wen-rongb,ZHONG Xian-youb
(a.Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance;b. Hubei Provincial Collaborative Innovation Center for New Energy Microgrid,China Three Gorges University,Yichang Hubei 443002,China)
Abstract:Aimed at the problem that the multi-class fault feature of rolling bearings are difficult to be effectively identified,a fault diagnosis method of rolling bearing based on local tangent space arrangement(LTSA)and wavelet support vector machine(WSVM)is proposed.The feature sets are constituted of the frequency band energy decomposed by Ensemble Empirical Mode Decomposition(EEMD).Firstly,it uses the local tangent space alignment for high dimension reduction.Then,the low-dimensional sensitive fault features are extracted from the original fault feature set.Finally,those low dimensional sensitive fault features are inputted into the wavelet support vector machine for rolling bearing multi-class fault identification.The experimental results show that the rolling bearing fault diagnosis method based on the LTSA and WSVM can effectively extract more low-dimensional sensitive fault features,and the fault diagnosis accuracy is higher than that of the traditional diagnosis method.
Key words:local tangent space alignment;wavelet support vector machine;roller bearing;fault diagnosis
文章编号:1001-2265(2016)06-0106-05
DOI:10.13462/j.cnki.mmtamt.2016.06.028
收稿日期:2015-11-16
*基金项目:国家自然科学基金(51405264,51205230);三峡大学人才启动基金(KJ2014B007);湖北省教育厅项目(B2015248)
作者简介:陈法法(1983—),男,湖北秭归人,三峡大学副教授,硕士生导师,博士,研究方向为机电系统动态测试与故障诊断,(E-mail)chenfafa2005@126.com。
中图分类号:TH165;TG65
文献标识码:A
