阀控缸式液压电梯的振动响应分析

刘　忠，高站伟，刘军军，霍沅明，赵　飞

（1.常熟理工学院机械工程学院，江苏常熟215500；2.苏州大学机电工程学院，江苏苏州215021）

阀控缸式液压电梯的振动响应分析

刘忠1，2，高站伟2，刘军军1，霍沅明2，赵飞1

（1.常熟理工学院机械工程学院，江苏常熟215500；2.苏州大学机电工程学院，江苏苏州215021）

摘要：阀控式液压电梯系统作为机械与液压的耦合体，振动现象不可避免.然而液压电梯的振动经常被忽略，本文针对液压电梯系统，通过建立两自由度的振动模型，分析了液压电梯轿厢的振动响应特性，综合考虑了惯性力和油液脉动力对轿厢振动位移与振动加速度的影响.在分析惯性力对轿厢振动响应影响时，主要考虑了不同载荷变化以及不同的速度曲线轿厢的振动情况；以油液脉动力作为外部激振力时，分析了不同固有频率的激振力对液压系统轿厢振动响应情况.通过理论分析和仿真实验，为解决液压电梯振动问题提供了理论依据和设计参考.

关键词：阀控缸；液压电梯；仿真；振动响应

1　液压电梯振动模型分析

对液压电梯进行振动分析时，由于系统具有较大的动态负载，液压油的刚度对系统具有重要的影响，所以不可忽略；并且轿厢架与轿厢之间的橡胶减震垫一般均匀分布在轿厢底框上，可等效为一个作用弹簧，因此，阀控式直顶液压电梯的结构可简化为两自由度的振动模型［1］，如图1所示.

图1　阀控式直顶式液压电梯振动分析模型

根据图1所建立的振动分析模型，对系统中的m1、m2进行受力分析，取两质量块静平衡位置为坐标原点，x1、x2为两质量块振动位移，两个外力F1和F2分别作用在m1和m2上，m1和m2的受力分析分别如图2所示.

根据牛顿第二定律可得，两个质量块的运动微分方程：

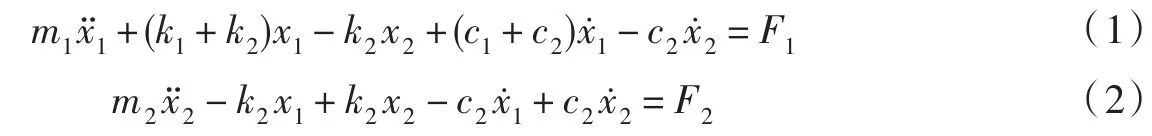
可以看出，方程（1）中含有x2项，同时方程（2）中含有x1项，所以它们是一个耦合的微分方程；m1的运动情况将会影响m2的运动状态，m2的运动反过来同时也会影响m1的运动.可将式（1）和（2）整理成如下矩阵形式的振动微分方程［2-4］：

｛X｝ =｛x1,x2｝T，是振动位移向量；｛F｝ =｛F1,F2｝T，是系统外部激振力向量；

图2　质量m1、m2的受力分析

2　液压电梯系统的振动响应分析

在分析计算液压电梯的振动响应特性时，液压电梯受到的外部激励较为复杂，外部激励的幅值、相位以及频率都很难确定.因此，对液压电梯进行振动响应特性分析的主要意义在于系统在定性的情况下，研究外界各种激励下系统振动的运动规律，而且阻尼参数对这种规律影响较小［3］.

将系统中的阻尼视为比例粘性阻尼，根据［C］ =α×［K］ +β×［M］可计算阻尼参数，式中α、β为瑞利阻尼系数，由于系统阻尼较小，可取α= 0.01、β= 0，因此可确定［C］ = 0.01×［K］ .本文主要研究液压电梯系统在外部变化的激振力下，轿厢产生的振动位移和振动加速度［5-6］.

在计算液压电梯系统的振动响应时，由于液压油液的刚度随轿厢的位置在不断变化，外部的激振力也是时变的，所以需要借助计算机来进行编程求解.利用MATLAB中微分方程的龙格-库塔数值解法，即“ode”函数可进行求解.将两个耦合的二阶微分方程（3）应改写成一个耦合的一阶微分方程.为此需引入新的变量：y1= x1，y2=̇1，y3= x2，y4=̇2；据此，式（1）和（2）可写成如下形式：

所以式（3）可以重写为：

3　电梯在惯性力激励下轿厢振动响应仿真分析

电梯在启动或制动的过程中，需要有一段加速段后才能进入匀速行驶或是有一段减速段后才能静止停靠.在此过程中产生的惯性力即为电梯系统外部激振力的一种形式，针对惯性力对电梯系统的振动响应进行仿真分析.此时，F1= m1a（t），F2= m2a（t），a（t）为电梯运行的加速度.由此可见，外部惯性力与加速度的大小有关，因此需要合理选取电梯的速度曲线［8］.

3.1电梯速度曲线的选择

电梯速度曲线的设计对电梯运行时的效率和舒适性有重要影响，所以应该合理设计电梯速度曲线.在曳引电梯的GB/T 10058-2009《电梯技术条件》中规定：电梯在起动加速度和制动减速度时，其最大值不大于1.5 m/s2；另外，人们的舒适感受加速度变化率的影响也较大，其规定加速度变化率最大值不得大于1.3 m/s3.虽然对液压电梯没有具体的规定要求，但《电梯技术条件》中对电梯速度的要求同样适用于液压电梯［9-10］.

电梯的上行、下行曲线一般由加速段、匀速段、减速段组成.目前速度曲线的主要形式有梯形速度曲线、抛物线速度曲线和抛物线直线速度曲线，还有加速度变化连续较为复杂的正弦速度曲线.

3.1.1抛物线-直线速度曲线

采用抛物线-直线速度曲线，其速度曲线、加速度曲线、加速度变化曲线如图3所示.

根据所研究的电梯设计要求，阀控式液压电梯最大匀速度为0.4 m/s，最大加速度为0.4 m/s2，加速度的变化率为0.8 m/s3，运行高度为2.62 m，可计算出电梯的速度和加速度：

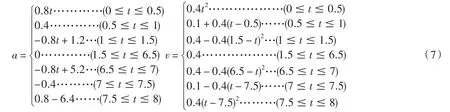
1）由于轿厢的振动会直接影响到轿厢内的乘客乘梯舒适性，所以主要分析轿厢的振动位移和振动加速度.电梯空载工况运行时，电梯在惯性力作用下轿厢产生的振动位移和振动加速度如图4所示.电梯满载工况运行时，电梯在惯性力作用下轿厢产生的振动位移和轿厢振动加速度如图5所示.

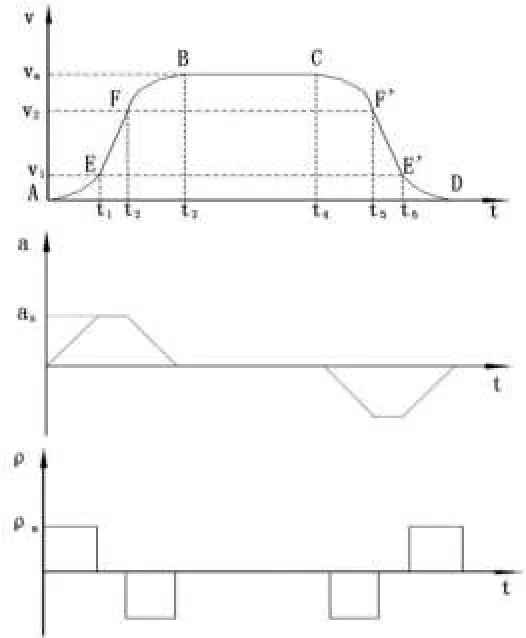
图3　抛物线-直线速度综合曲线

图4　空载工况轿厢振动情况仿真结果

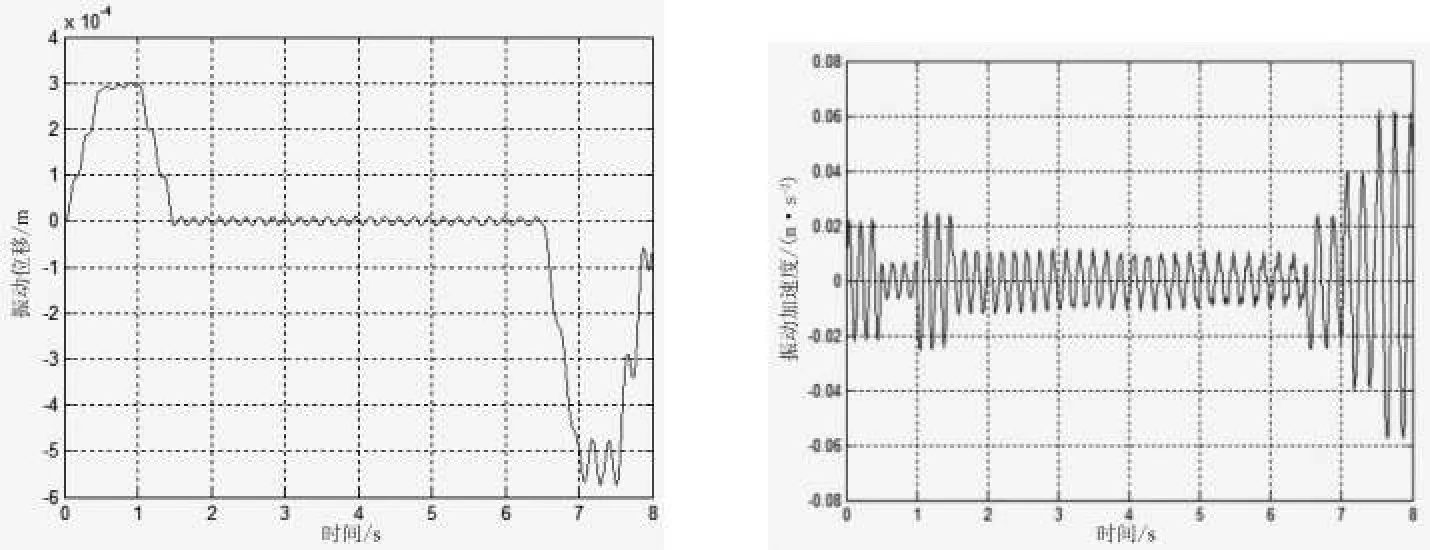
图5　满载工况轿厢振动情况仿真结果

为了能够更好地分析电梯在不同载荷下对轿厢振动位移和振动加速度的影响，对空载与满载的振动情况进行对比仿真，如图6所示.

3.1.2抛物线速度曲线

采用抛物线速度曲线，系统在惯性力的作用下，轿厢所产生的振动响应曲线如图7所示.

确定电梯的最大匀速度vm为0.4 m/s；最大加速度am为0.4 m/s2；加速度的变化率为0.4 m/s3；则可计算出电梯的速度和加速度如式（8）所示.

以这种速度曲线为例，轿厢空载时在惯性力的作用下轿厢产生的位移和振动加速度如图8所示.

3.2仿真实验结果

根据上述仿真实验，可得如下结果：

1）从仿真结果图4、图6进行分析：电梯轿厢的振动位移主要受电梯运行加速度的影响，在启动和制动过程的振动位移较大，电梯匀速运行时振动位移很小.在前面已经得知，液压油液刚度系数会随着电梯的上升有所减小；由此，导致电梯上升在减速段时轿厢的振动位移相对加速段时轿厢的振动位移有所增大.

2）从仿真图6可以看出电梯满载时的振动位移相比空载工况时轿厢的振动位移大一些.造成这样的仿真结果，可能是由于轿厢质量的增大使轿厢受到的惯性力有所增加，因此在启动或制动时导致轿厢的振幅变大.

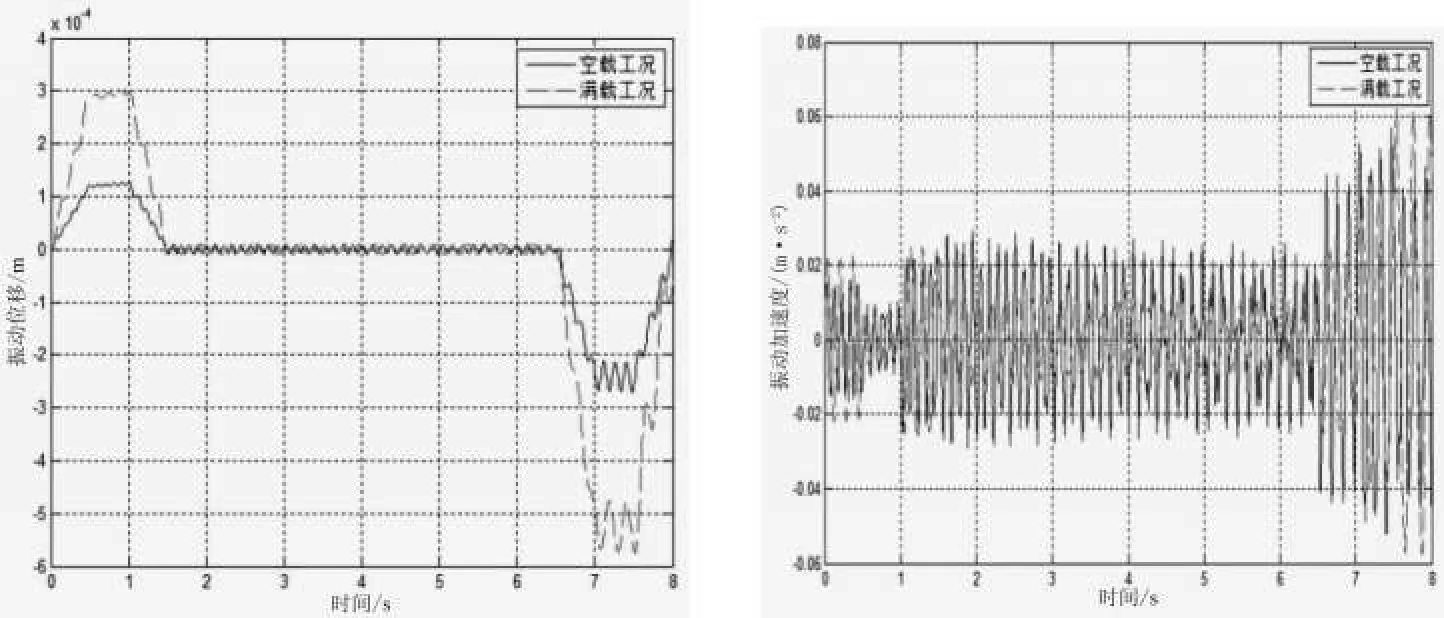
图6　不同载荷下轿厢振动对比仿真结果

图7　抛物线速度综合曲线

图8　抛物线速度曲线下的轿厢振动响应

3）从仿真结果图4、图5可看出轿厢在制动时的振动加速度较大，最大值在0.06 m/s左右.电梯在空载工况匀速运行时，轿厢的振动加速度与满载工况匀速运行时相比较大，这说明载重增加可以减小液压电梯匀速运行时轿厢的振动加速度.

4）从图6两种工况下振动加速度的对比情况来看，电梯空载与满载时相比轿厢的振动加速度变化频率较大，此时的轿厢振动较为强烈.

5）仿真结果图8与仿真结果图4进行对比分析，在工况条件相同情况下，采用不同的速度曲线，对轿厢的振动位移和振动加速度都有影响；采用第二种速度曲线方式，轿厢的振动位移与振动加速度都有减少，虽然振动位移减少得不是特别明显，但是轿厢的振动加速度有较大的降低，最大值为0.03 m/s2；与第一种速度曲线产生的振动加速度最大值0.06 m/s2相比有了较大的改善.所以，为了提高液压电梯的平稳性，减少制动时的振动，应合理选择速度曲线并设置合理的速度曲线参数.

4　电梯轿厢在液压脉动力激励下振动响应仿真分析

在对曳引电梯进行振动分析时，电梯系统的驱动装置是一个主要的激振源.所以在对液压电梯分析时，同样考虑驱动装置作为一个主要的激振源来进行分析.在该系统中液压电梯的速度是由比例阀控制进入油缸内的流量来达到理想速度的控制，故比例阀与油缸容腔构成了一个压力区，其流量连续性方程为

式中：p为液压油缸内的压力；E为液压油的弹性模量；V为容腔体积；Q为流入液压缸的流量；v为柱塞的速度；A为油缸柱塞的有效作用面积.

由式（9）可知，比例阀在控制流量时产生的流量脉动最终体现在液压缸内的压力变化.因此，液压电梯驱动装置作为外界激励源主要来自油缸内油液压力的脉动.为了简化分析，假设油液脉动力满足简谐规律，油液对柱塞缸的激振力为F1= F sin ωt .

以电梯空载工况为例，探寻不同固有频率的简谐激振力对系统振动响应的影响.为了分析液压系统油液脉动力作为外部激振源对电梯振动的影响，采用不同频率的激振力对系统进行仿真分析.

4.1振动位移与振动加速度仿真结果

1）当液压脉动力的固有角频率为10 rad/s，简谐激振力F1=50sin10t作用时，轿厢的振动位移与振动加速度仿真结果如图9所示.

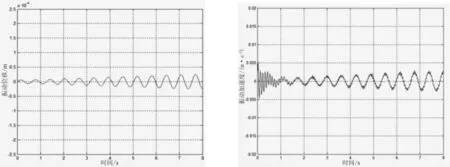
图9　激振力F1=50sin10t作用下，轿厢的振动响应

2）当液压脉动力的固有角频率为50 rad/s，简谐激振力F1=50sin50t作用时，轿厢的振动位移与振动加速度仿真结果如图10所示.

图10　激振力F1=50sin50t作用下，轿厢的振动响应

3）当液压脉动力的固有角频率为90 rad/s，简谐激振力F1=50sin90t作用时，轿厢的振动位移与振动加速度仿真结果如图11所示.

4）当液压脉动力的固有角频率为150 rad/s，简谐激振力F1=50sin150t作用时，轿厢的振动位移与振动加速度仿真结果如图12所示.

5）当液压脉动力的固有角频率为300 rad/s，简谐激振力F1=50sin300t作用时，轿厢的振动位移与振动加速度仿真结果如图13所示.

4.2仿真实验结果分析

1）当外部激振力的角频率为10 rad/s时，此时外部激振力的角频率在系统1、2阶固有角频率变化的范围之外，轿厢的振动位移很小，最大值为0.03 mm.当外部激振力的角频率为50 rad/s时，此时外部激振力的角频率在系统1阶固有角频率43～62 rad/s范围内，导致轿厢的振动位移较大，最大振动位移在0.3 mm左右.当外部激振角频率为90 rad/s时，此时的激振角频率在系统1阶固有角频率最大值与系统2阶固有角频率最小值之间，避开了系统的1阶与2阶固有频率，使轿厢的振动位移同样很小，最大值为0.02 mm.当外部激振力的角频率为150 rad/s时，虽然此时激振力的角频率在系统2阶固有角频率变化范围内，但是轿厢的振动位移没有明显增大，在激振力角频率与系统2阶固有频率接近时略有增大，但最大值为约0.01 mm.当外部激振力的角频率为300 rad/s时，远远大于系统的固有角频率，轿厢的振动位移变化非常小，可以忽略不计.

系统的1阶固有频率对轿厢的振动位移影响较大，当外部激振力的角频率在系统的1阶固有角频率变化范围内时，轿厢的振动位移会有明显的增大.随着外部激振力角频率的增加，远离系统1阶固有频率时，可以降低轿厢的振动位移，且系统2阶固有频率对轿厢振动位移的影响较小.

图11　激振力F1=50sin90t作用下，轿厢振动加速度

图12　激振力F1=50sin150t作用下，轿厢的振动响应

图13　激振力F1=50sin300t作用下，轿厢的振动响应

2）油液激振力的角频率对轿厢振动加速度的影响：当油液激振力角频率为10 rad/s时，轿厢振动加速度很小，不到0.005 m/s2；当油液激振力角频率为50 rad/s时，其激振力频率在系统1阶固有频率变化范围内，轿厢振动加速度有明显增大，轿厢最大振动加速度可达到0.7 m/s2；当油液激振力角频率为90 rad/s时，轿厢的振动加速度也较小为0.1 m/s2左右；但是当油液激振角频率为150 rad/s时，其激振力角频率在系统2阶固有角频率变化范围内，激振力角频率在接近与系统固有角频率相同位置时，轿厢的振动加速度达到最大值约为0.2 m/s2；当外部激振力角频率为300 rad/s时，其远远大于系统的各阶固有角频率，对系统轿厢的振动加速度影响同样很小，可以忽略.

油液激振角频率在系统固有角频率变化范围内时，会大大增加轿厢的振动加速度，尤其是与系统1阶固有频率相同时；系统的1阶固有角频率对轿厢的振动加速度影响较大.当外部激振力的角频率远离系统各阶固有角频率变化范围时，大大减缓了对轿厢振动加速度的影响.

通过以上分析可知，由于液压缸油液等效刚度的连续性，使得液压电梯系统的固有频率在一个连续的范围内变化；当油液的激励角频率与系统固有角频率接近时，容易引起系统的共振，使得轿厢的振动位移和振动加速度都有明显增加.为了减少压力脉动对轿厢的振动影响，应使激励的频率远离这一特定的范围.

5　结语

对液压电梯的振动特性进行了理论分析，首先建立了两自由度的振动模型，考虑到液压缸柱塞行程的变化使液压缸内的油液等效刚度发生变化，分析了液压缸内油液等效刚度变化、载重变化对系统固有频率的影响.在对液压电梯轿厢的振动响应分析时，重点考虑了惯性力和油液脉动力对轿厢振动位移与振动加速度的影响.在分析惯性力对轿厢振动响应影响时，主要考虑了不同载荷变化以及不同的速度曲线下轿厢的振动情况.在分析油液脉动力作为外部激振力时，重点分析了不同固有频率的激振力对系统轿厢振动响应情况.这些理论分析为解决液压电梯实际运行时产生的振动问题提供了一定的理论参考.

参考文献：

［1］沈娇，汪军.基于Simulink的单缸驱动液压电梯振动分析［J］.机械研究与应用，2012（6）：23-25.

［2］张长友，朱昌明.电梯系统动态固有频率计算方法及减振策略［J］.系统仿真学报，2007，19（16）：3856-3859.

［3］于德介.机械振动学［M］.长沙：湖南大学出版社，2010：25-30.

［4］刚宪约.曳引电梯系统动态理论及动力学参数优化方法研究［D］.杭州：浙江大学，2005.

［5］INABA H, SHIGETA M. Attitude control system of a super-high speed elevator car based on magnetic guides［J］. IECON Proceedings, 1994（2）：1028-1033.

［6］LORSBACH G P. Analysis of elevator ride quality［J］. Vibration Elevator World, 2003,51（6）：108, 110-111, 113.

［7］武丽梅，巩煜琰，李雪枫.曳引式电梯机械系统垂直振动动态特性分析［J］.机械设计与制造，2007，10：16-18.

［8］刘希花，任勇生，单淮波.电梯系统垂直振动动态特性研究［J］.山东科技大学学报，2010，29（1）：62-66.

［9］KIM C S, HONG K S, KIM M K. Nonlinear robust control of a hydraulic elevator：experiment-based modeling and two-stage Lyapunov redesign［J］. Control Engineering Practice, 2005（13）：789-803.

［10］贺文海.液压电梯垂直振动特性仿真分析［J］.机床与液压，2010，38（2）：81-82.

A Vibration Response Analysis of Hydraulic Elevator with Valve Control Cylinder

LIU Zhong1,2, GAO Zhanwei2, LIU Junjun1, HUO Yuanming2, ZHAO Fei1
（1. School of Mechanical Engineering, Changshu Institute of Technology, Changshu 215500, China；2. School of Mechanical Engineering, Soochow University, Suzhou 215021, China）

Abstract：As a mechanical and hydraulic coupling, the vibration phenomenon of the valve controlled hydraulic elevator system is inevitable. However, the vibration of hydraulic elevator is often ignored. According to the researched hydraulic elevator system, the vibration response characteristics of the hydraulic elevator car are analyzed through building a two-degree-of- freedom vibration model. The influence of inertia force and oil pressure on the vibration displacement and acceleration of the car is comprehensively considered. Based on the analysis of the influence of the inertia force on the vibration response of the car, the vibration of the car with different loads and different speed curves is mainly considered. When the oil pulse is used as the external exciting force, an analysis is made of the influence of the exciting force of different natural frequencies on vibration response of the hydraulic elevator car. Through theoretical analysis and simulation experiments, a theoretical basis and design reference is provided for solving the vibration problem of hydraulic elevator.

Key words：valve control cylinder；hydraulic elevator；simulation；vibration response

中图分类号：TU857

文献标识码：A

文章编号：1008-2794（2016）02-0009-07

收稿日期：2015-12-26

基金项目：国家自然科学基金“中深孔液压凿岩设备设计理论与若干关键技术研究”（51275060）；苏州市科技计划项目“自激励液压凿岩机关键技术研究”（SYG201325）；常熟理工学院自制仪器科研项目（cg201411）

通信作者：刘忠，教授，工学博士，研究方向：现代工程装备设计、机电液压系统集成与节能控制，E-mail：liuzhong678@ 163.com.