汽车四轮转向的最优控制研究

陈庆樟，孟　杰，刘臣富

（1.常熟理工学院机械工程学院，江苏常熟215500；2.天津职业技术师范大学，天津300222）

汽车四轮转向的最优控制研究

陈庆樟1，孟杰1，刘臣富2

（1.常熟理工学院机械工程学院，江苏常熟215500；2.天津职业技术师范大学，天津300222）

摘要：为提高四轮转向汽车的操纵稳定性，提出一种最优控制方法.建立了汽车四轮转向二自由度模型，同时基于二次型最优控制理论，建立了四轮转向系统的最优控制模型.在MATLAB/ Simulink环境下进行了仿真.仿真结果表明：相比传统的前轮转向，采用基于最优控制的的四轮转向系统能改善车辆的行驶姿态，实现了零侧偏角控制目标，同时横摆角速度的控制误差也很小，使得汽车具有更好的行驶轨迹、速度保持能力和稳定状态，进一步提高了车辆的操纵性能.

关键词：四轮转向汽车；最优控制；操纵稳定性

1　引言

四轮转向（Four-wheel steering，4WS）汽车的转向任务是由前轮和后轮共同完成.如果在汽车转弯时只靠两个前轮转向，车尾就会产生较大的侧滑和摆尾，这对汽车的安全行驶相当不利. 4WS的实现使得在低速行驶时可以使前轮与后轮转角方向相反，从而改善汽车的操作性；在中高速行驶时可以使前轮与后轮的转角方向相同，从而减小汽车的侧滑和摆尾，提高汽车转向时的操纵稳定性.

近年来随着电子技术、测试技术、系统动力学等学科的快速发展，车辆4WS系统的控制技术发展很快.迄今为止，人们针对主动后轮转向的4WS控制问题，提出了前后轮转角成比例的前馈控制、横摆角速度反馈控制、神经网络控制等方法［1-4］.直接横摆力矩控制（DYC）也是当前汽车动力学系统稳定控制中一种较为有效的汽车底盘控制技术，它通过对轮胎纵向力的分配产生横摆力矩以调节车辆的横摆运动，从而确保汽车行驶稳定性.目前，有关采用横摆力矩控制汽车稳定性的报道也较多，其中包括神经网络控制、模糊控制等.采用常规模糊控制在控制精度上不够理想，且模糊规则难以建立；而以神经网络为代表的智能控制技术的高度复杂性使得不可能精确分析它的各项性能指标，大大限制了其应用范围，且体系通用性差，每种神经网络只适应于一种或几种类型.同时神经网络还需要在训练样本的获取、网络模型的具体构造以及学习训练策略等方面不断加以完善.

现代控制理论中的最优控制应用范围较广泛，其理论基础也比较完善，其中的线性二次型调节器1inear quadratic regulator，LQR）的控制算法能够通过给出所需的最优性能指标，确定系统状态变量和控制变量的加权矩阵，为设计者提供了一定的设计空间. LQR方法应用在车辆四轮转向设计中，可以由不同的性能需要来提出不同的目标函数，确定相应的加权矩阵，即LQR方法可以通过综合考虑车辆四轮转向系统中的各种因素达到对车辆操纵性能的改善.

2　汽车四轮转向二自由度模型

根据自由度不同，汽车的4WS模型可以分为二自由度、三自由度以及多自由度模型.低自由度车辆模型研究比较简单，但不能很好反应出汽车的运动状态，而高自由度模型虽然能较好反映出汽车的运动状况，但是研究的难度也相应变大了.因此选取适合的自由度作为研究对象建立汽车动力学模型显得十分重要.本文主要以4WS二自由度模型为研究对象.

如图1所示，不考虑悬架的影响，假定汽车只做平行于地面的平面运动，即汽车只有绕质心的横摆运动和沿y轴的侧向运动.另外，汽车的侧向加速度控制在0.5 g以下.

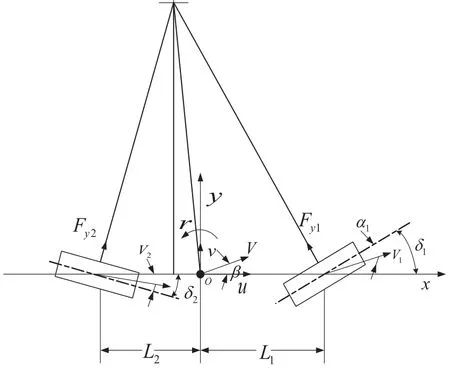
图1　二自由度四轮转向汽车模型

运动微分方程为：

式（1）和图1中：M为整车质量；V为车速；u为沿x轴方向的前进速度；v为沿y轴方向的侧向加速度；β= v/u为质心处的侧偏角；r为横摆角速度；IZ为绕质心的横摆转动惯量；δ1和δ2分别为前、后轮转角；L1和L2分别为质心至前、后轴的距离；Fy1和Fy2分别为前、后轮侧偏力.

因为前、后轮转角较小，可近似认为cos δ1= 1，cos δ2= 1，则式（1）可写为：

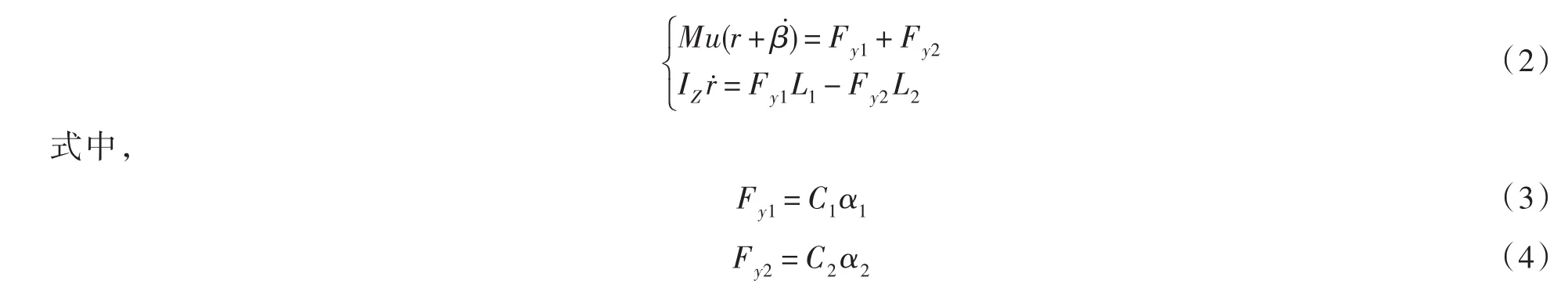
其中，C1、C2分别为前、后轮的轮胎侧偏刚度，取负值；α1、α2分别为前、后轮胎侧偏角. α1=β+（L1/u）r-δ1，α2=β+（L2/u）r-δ2.

将式（3）、式（4）代入式（2）中、得到如下运动微分方程：

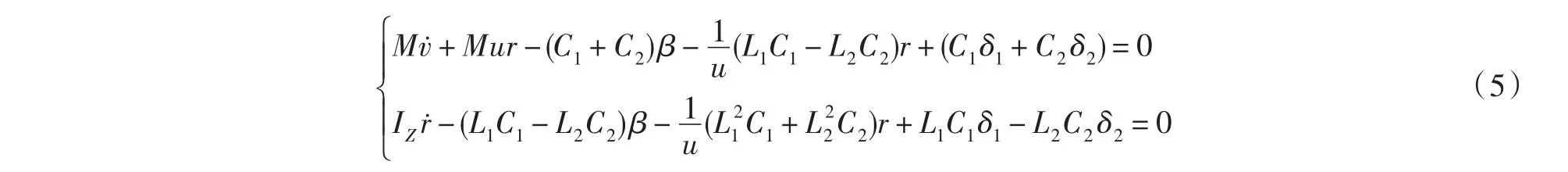
当后轮转角δ1= 0时，该系统即为二轮转向系统.

定义i为前后轮转向比［5］

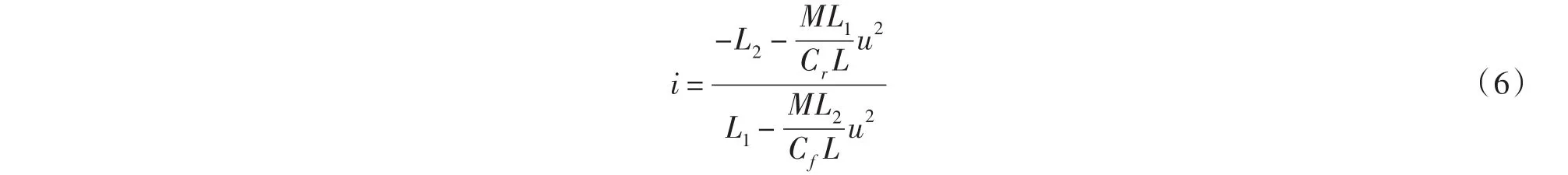
则4WS汽车后轮转角δ2= iδ1，且|i|＜1.当i为正时，即0＜i＜1时为前后轮同方向转向；当i为负时，即-1＜i＜0时为前后轮反方向转向.则式（5）可变化为：

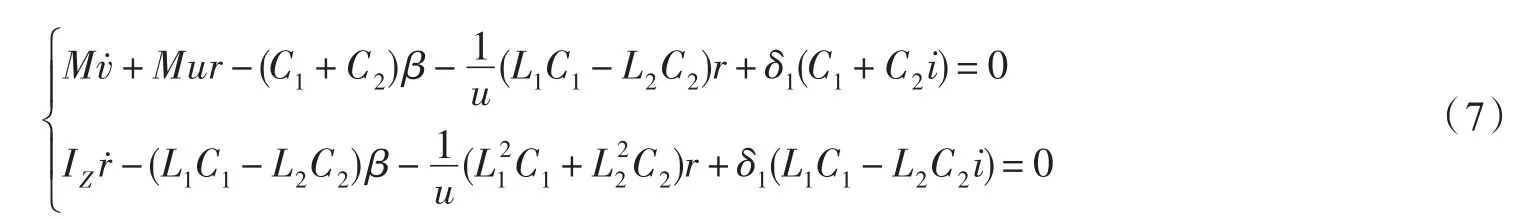
式（7）形式虽然简单，却考虑了轮胎的侧偏刚度、汽车质量、质心位置和绕质心的转动惯量这些重要参数，能够对4WS汽车转向运动的基本特征进行正确描述.

3　4WS系统状态空间方程的建立

汽车四轮转向系统的最优控制的实现，必须以建立四轮转向模型的状态空间表达式为前提.

采用同样的二自由度汽车四轮转向模型，汽车可被视为投影在地面的忽略高度的两轮车.假设汽车行驶速度不变，忽略汽车的俯仰和侧倾运动的影响，只研究它的横摆和侧向运动.则所建立模型的运动微分方程如式（2）所示.

运动方程表明：车辆的侧向运动主要受前、后轮转角的影响；车辆的横摆运动主要受前、后轮差的影响.控制器是根据横摆速度和质心侧偏角来协调前后轮转角.

前、后轮的转角可以由以下公式给出：

式（8）中，δs为驾驶员通过方向盘传给前轮的角阶跃输入；δc为控制器输入的起反馈作用的转角；Kc为控制器对前、后轮的输入分配比.如果Kc变化，前、后轮转角的和仍保持不变.因此Kc的变化对车辆的侧向运动基本不会产生影响.

选取状态变量X =［β,r］T，输出变量Y =［β,r］T，由微分方程式（2），并将式（8）代入，可以写出状态方程为：

4　4WS系统最优控制模型的建立

最优控制（optimal control）是指根据系统的现有条件，采取综合方法，实现各项性能指标的最优化.对于汽车4WS系统而言，最优控制能够很好地适应.

4WS的最优控制问题是：在已知系统参数和初始条件的情况下，寻找一个最优控制，使4WS系统工作性能指标达到理想值.

可以视汽车4WS的最优控制器为一个终了时间tf→∞的线性调节器，在这样的规定下，得出的是线性定常的最优反馈规律，要求求解的黎卡提（Riccati）方程也是代数方程.

最优控制的性能参数指标应取二次函数积分型.控制的目标是使侧偏角达到最小值，因此性能指标就可以写为：

由最优控制理论可知，若控制输入

则性能指标J为最小，其中K = R-1BTL，称为最优反馈增益矩阵，这里L是下列Riccati矩阵方程的解.

5　模拟仿真与结果

本文选取Kc= 0.5，权系数q = 50，V=20 km/h，前轮转角δs为单位阶跃输入进行MATLAB仿真.具体模型数值设置如表1所示.

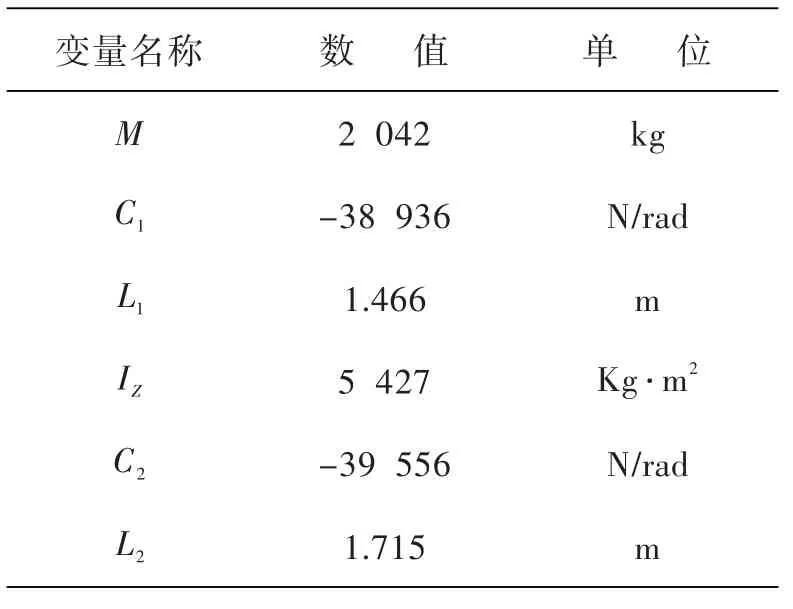
表1　汽车模型参数设置

由图2和图3可以看出，采用最优控制的4WS车辆的质心偏侧角瞬态响应性能得到很大改善，到达稳态值所消耗的时间较短，超调量明显减少，很好地控制了汽车的运动姿态，而4WS汽车的横摆角速度响应与2WS汽车基本保持一致，这样可以使驾驶员原有的转向感觉得到很好的保持.

同时，采用最优控制的4WS汽车的质心偏侧角比较小，可以有效地保证质心偏侧角接近于零. 4WS汽车的横摆角速度响应迅速，驾驶员的转向意图得到很好的实现，同时准确地跟踪了希望获得的横摆角速度.

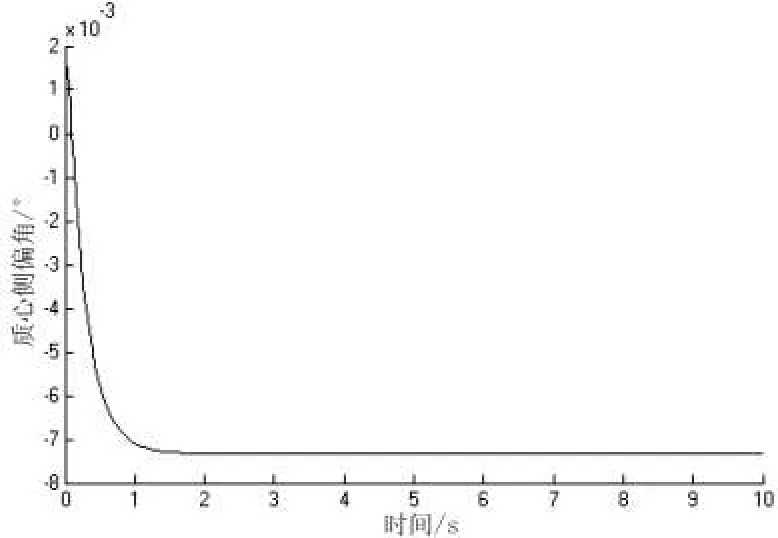
图2　质心偏侧角响应曲线

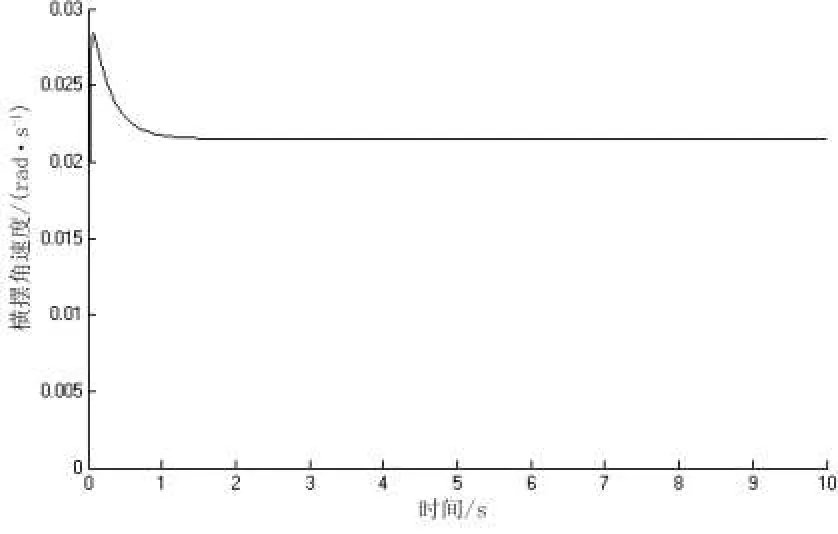
图3　横摆角速度响应曲线

6　结论

通过建立汽车四轮转向二自由度模型，基于二次型最优控制理论，建立四轮转向系统的最优控制模型，根据系统的现有条件，采取综合方法，对各项性能指标进行最优化.改善了车辆的行驶姿态，实现了零侧偏角控制目标，同时横摆角速度的控制误差也很小，使得汽车具有更好的行驶轨迹、速度保持能力和稳定状态，进一步提高了车辆的操纵性能.

该方法可以有效地保证极小的质心偏侧角.使得4WS汽车的横摆角速度响应迅速，驾驶员的转向意图得到很好的实现，同时准确地跟踪了希望获得的横摆角速度.

参考文献：

［1］王振刚，范健文，高远，等.四轮转向车辆操纵稳定性的最优控制策略研究［J］.广西科技大学学报，2015，26（1）：1-5.

［2］SANO S, FURUKAWA Y, SHIRAISHI S. Four Wheel Steering System with Rear Wheel Steer Angle Controlled as a Function of Steering Wheel Angle［J］. SAE Technical Paper, 1986：860625.

［3］FURUKAWA Y, YUHARA N, SANO S, et al. A Review of four Wheel Steering Studies from the Viewpoint of Vehicle Dynamics and Control［J］. Vehicle System Dynamics, 1989, 18：151-186.

［4］韩振南，陈光.基于神经网络三自由度非线性四轮转向汽车控制仿真［J］.机械设计与制造，2011（11）：224-227.

［5］刘竞一.汽车四轮转向模式及智能控制技术研究［D］.重庆：重庆交通大学，2008.

An Optimal Control of the Vehicle Active Suspension Based on the Simulated Annealing Algorithm

CHEN Qingzhang1, MENG Jie1, LIU Chenfu2
（1. School of Mechanical Engineering, Changshu Institute of Technology, Changshu 215500, China；2. Tianjin Vocational Technology Normal University, Tianjin 300222, China）

Abstract：Aiming at improving the steering stability of four-wheel-steering（4WS）vehicle, an optimal control method is presented in this paper. A 4WS vehicle model is set up, together with optimal control model based on a simplified linear model. Under the circumstances of MATLAB/Simulink, simulation is provided. And the results show that, under the driving cycles, the 4ws system can get better characteristics compared to the 2ws, such as zero slip angle and the smaller error of yaw velocity, and can also further enhance the path tracking ability and steering stability of 4WS vehicle.

Key words：four-wheel-steering vehicle；optimal control；steering stability

中图分类号：U463

文献标识码：A

文章编号：1008-2794（2016）02-0004-05

收稿日期：2015-12-26

基金项目：江苏省自然科学基金“电机再生制动与液压制动防抱死耦合机理研究”（BK20151259）

通信作者：陈庆樟，教授，博士，研究方向：汽车机电一体化技术，E-mail：cqz@cslg.cn.