改进的自适应小波阈值去噪新算法

辛元超　张君安　方　舟

(西安工业大学机电工程学院　西安　710021)

改进的自适应小波阈值去噪新算法

辛元超张君安方舟

(西安工业大学机电工程学院西安710021)

摘要针对软硬阈值去噪算法中存在的边缘模糊等问题,分析含噪图像中噪声的分布特点,提出了基于最小均方算法的自适应去噪新算法。该算法基于分层理想阈值保留图像细节并抑制噪声,确定各个尺度级的自适应最佳阈值,提高峰值信噪比。实验对比表明:自适应小波阈值去噪新算法处理后图像的信噪比均提升了12%,图像去噪效果明显。

关键词小波变换; 自适应去噪; 阈值函数; 阈值去噪

Class NumberTP391.41

1引言

图像在拍摄过程中光线、灰尘等影响以及在图像的传输过程中都会产生噪声影响图像的质量,严重影响图像的处理以及分析,因此对图像进行小波去噪很有必要[1]。小波变换去噪的原理是根据图像噪声分布在不同频域的特点,选择合适的阈值,对小波系数进行调整,从而实现小波变换去噪。如式(1)所示,小波变换去噪是去噪函数在平移变换过程中不断逼近含噪信号,从而保留原始信号,去除噪声信号[2]。

(1)

其中,fs为原始信号,fn为噪声信号,opt为最优解。

由于噪声信号往往存在于高频通道中,所以用传统方法解决小波往往用低通滤波器对图像信号做低通道滤波,但是这种方法对小波原始信号损失较大。为了完好保留原始信号,现在往往先对含噪声信号进行特征提取获取信号中的特征信息,在通过低通滤波去除噪声信号,最终对信号进行重构[3]。如图1所示。

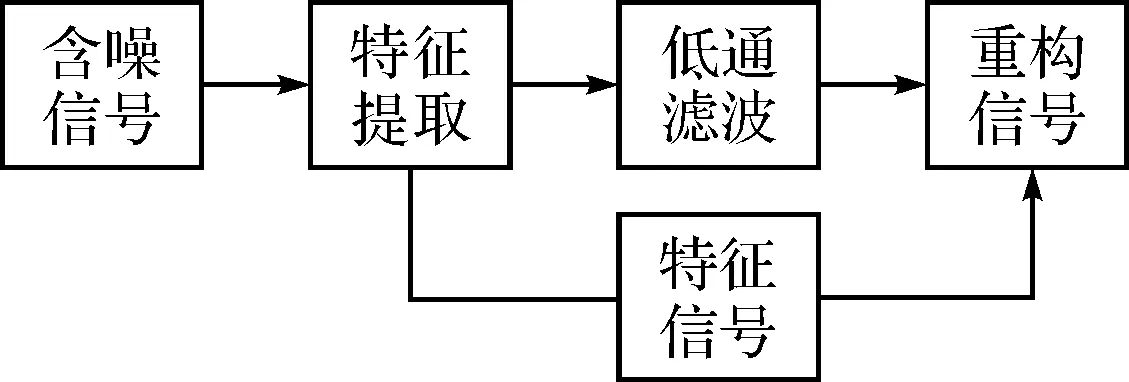
图1　小波去噪框架图

2小波阈值去噪

小波阈值去噪的的原理是根据信号s(k)和白噪声n(k)分布的不同,提出了阈值去噪法。阈值去噪法是将含噪信号进行小波分解,对存在于大尺度下的小波系数,保留低分辨率下的小波系数。而不同尺度下高分辨率的小波系数,设定一个合适的阈值λ,将小波系数Wj,k的绝对值与阈值λ数值做比较,若小波系数Wj,k的绝对值小于阈值λ,则小波系数Wj,k为0;若小波系数Wj,k的绝对值大于阈值λ,则对其做适当的收缩或者不做处理,得到估计小波系数Wj,k[4]。进而将小波系数通过小波逆变换处理做信号重构,得到去噪的信号,如图2所示为阈值收缩去噪的流程图。

图2阈值去噪流程图

小波阈值去噪的关键是选取合适的阈值以及用哪种方法进行阈值门限的处理。阈值门限的处理方法通常有硬阈值法和软阈值法。硬阈值是比较信号的绝对值与阈值之间的大小。如式(2)所示,比阈值λ大的点数值不变,反之则会变为0。

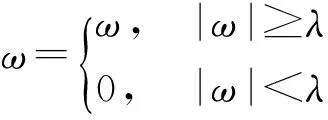
(2)

软阈值同样是比较信号值的绝对值与阈值之间的大小,如式(3)所示,只是当信号值的绝对值大于或等于阈值时,该点的值为信号值的绝对值与阈值的差。

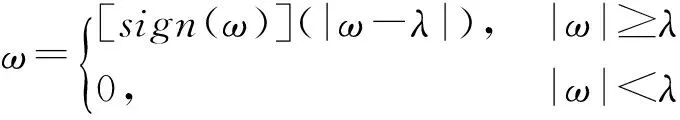
(3)

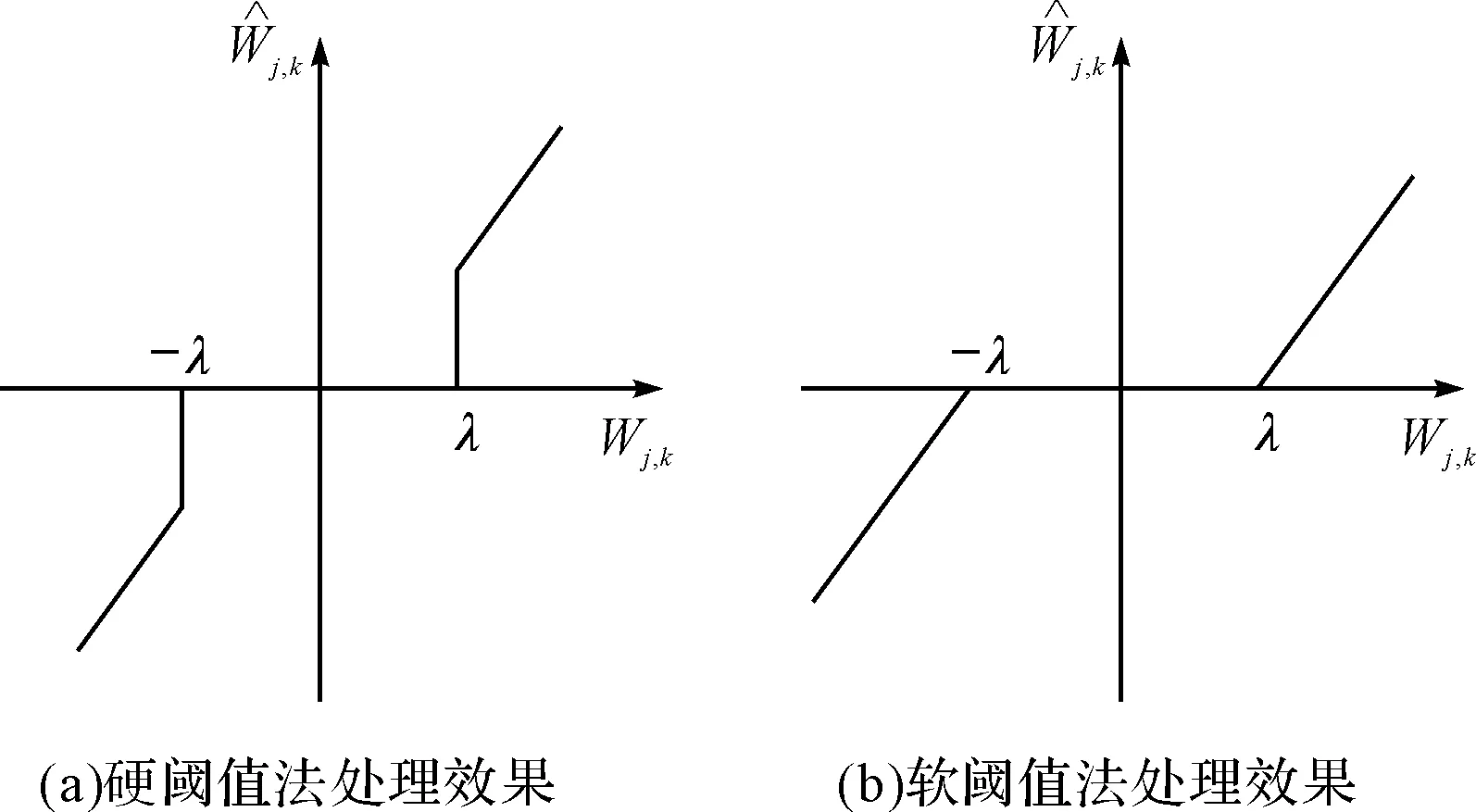
图3　两种阈值处理效果对比

3基于LMS准则的自适应去噪算法

基于LMS准则的小波去噪方法是基于小波阈值去噪法,通过最小均方误差LMS算法和Stein算法,构造一个可进行多阶连续求导的阈值函数[6],通过对阈值的迭代运算,计算最佳阈值。

3.1阈值函数的构造

(4)

因此,构建的阈值函数既要能进行函数连续求导,也要具有软硬阈值函数的优点,构造阈值函数为

(5)

由上式知,当β=0时,阈值函数去噪效果接近硬阈值函数。当β趋近无穷大时,阈值函数去噪效果与软阈值函数类似。构造的函数可连续求导。通过实验证明,当β取4,5,6时,可获得比较好的去噪效果。

3.2自适应去噪新算法

通过之前的分析知,噪声多存在于小波系数的高频部分,故只要对小波系数的高频部分做去噪处理就可去除噪声。因此,本文提出的去噪算法如下:

1) 对含噪图像X进行离散小波分解,得到系数向量。

Y=[AJ,HJ,DJ,HJ-1,VJ-1,DJ-1,…,H1,D1,V1]

2) 计算的各小波系数的长度,记为向量L。L(1)为低频系数A的长度,L(i)是水平高频系数H,垂直高频系数V和对角线高频系数D的长度之和(i=2,3,…,J+1),L(J+2,∶)是X的长度[8]。

3) 对小波系数的高频部分进行阈值处理。

(2)将高频系数存储在向量Cj中Cj=[Hj,Vj,Dj]

(3)按照式(6)计算Δλj(k)[9]。

(6)

(4)由式(4)得到λj(k)。

(5)用小波逆变换法将低频系数Aj与处理后的高频系数进行图像重构。

4实验结果及分析

图4中,令x轴为阈值λ=20,y轴分别为三种去噪算法的阈值函数,其中本文算法中的阈值函数β=5。由图中三种算法的阈值函数可知,本文算法在连续性上优于软阈值和硬阈值两种算法。

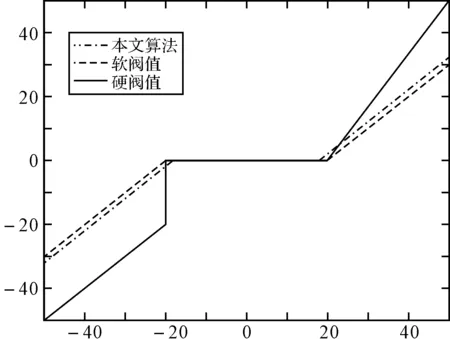
图4　三种算法阈值函数的对比

图5　三种去噪算法的对比

将噪声方差为0.02的Lena图像分别用软阈值去噪法,硬阈值去噪法和本文提出的去噪法进行对比。如图5所示,本文所提的去噪方法在图像细节的保留上比其他两种去噪法效果更好。

分别计算三种算法的峰值信噪比,通过数值比较三种算法的图像去噪质量。

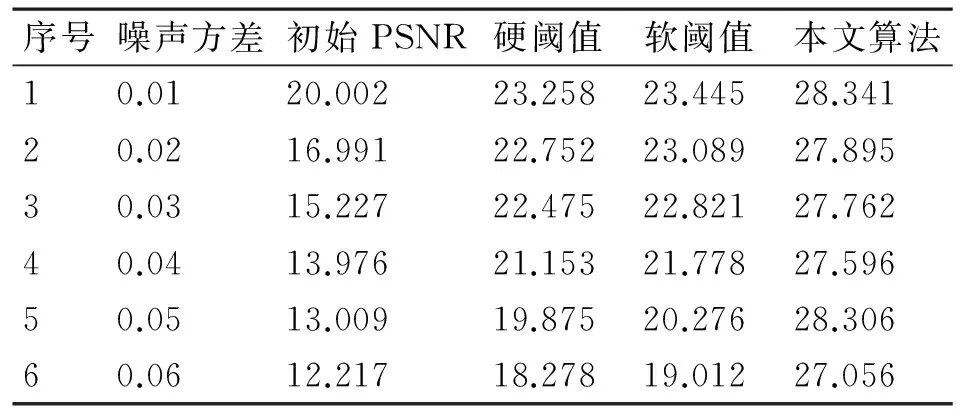
(7)其中I′(i,j)为含噪图像在(i,j)处的灰度值,I(i,j)是理想图像在(i,j)处的灰度值。m是图像的行数,n是图像的列数[10]。表1为三种去噪算法对lena图像的峰值信噪比PSNR对比。

5结语

针对软硬阈值去噪算法中存在的边缘模糊等问题,本文提出的去噪算法基于最小误差均方理论,使每层的阈值是最理想的阈值,从而保证图像细节信息的保留[11],并抑制了噪声,弥补了软阈值和硬阈值在去噪上的不足。通过处理效果对比以及实验结果证明,本文提出的算法在视觉效果以及信噪比等方面,都优于软硬阈值去噪算法,证明本文算法是完全可行的。

参 考 文 献

[1] 乔林峰,王俊.一种改进小波阈值的图像去噪算法[J].舰船电子工程,2013,33(1):55-56.

QIAO Linfeng, WANG Jun. An Image Denoising Algorithm Based on Improving Wavelet Thresholding[J]. Ship Electronic Engineering,2013,33(1):55-56.

[2] Patil P M, Sontakke T R. Rotation, scale and translation invariant handwritten Devanagari numeral character recognition using general fuzzy neural network[J]. Pattern Recognition,2007,40(7):2110-2117.

[3] Goyal M, Garg N K. Techniques for Recognition of Handwritten Devanagari Numeral[J]. International Journal of Advanced Research in Computer Science,2013,4(9).

[4] Verma K, Sharma R K. Performance Analysis of Zone Based Features for Online Handwritten Gurmukhi Script Recognition using Support Vector Machine[J]. Progress in Systems Engineering. Springer International Publishing,2015,330(6):747-753.

[5] 朱锡芳.一种基于连续小波阈值的图像去噪新算法[J].微电子学与计算机,2007,24(11):181-182.

ZHU Xifang. A Novel Algorithm for Image Denoising Based on Continual Wavelet Threshold Methods[J]. Microelectronics & Computer,2007,24(11):181-182.

[6] 李根强,黄永东,蒋肖.基于小波变换和脊波变换的自适应图像去噪算法[J].计算机应用研究,2012,29(8):3192-3194.

LI Genqiang, HUANG Yongdong, JIANG Xiao. Adaptive image denoising method based on wavelet transform and ridgelet transform[J]. Application Research of Computers,2012,29(8):3192-3194.

[7] Luisier F, Blu T. SURE-LET Multichannel Image Denoising: Interscale Orthonormal Wavelet Thresholding[J]. IEEE Transactions on Image Processing,2008,17(4):482-492.

[8] Kadiri M, Djebbouri M, Carré P. Magnitude-phase of the dual-tree quaternionic wavelet transform for multispectral satellite image denoising[J]. Eurasip Journal on Image & Video Processing,2014,2014(1):1-16.

[9] 李柯材,张曦煌.基于邻域阈值萎缩法的图像去噪方法的优化[J].计算机应用,2010,30(1):78-81.

LI Kecai, ZHANG Xihuang. Optimized image denoising method based on neighborhood threshold shrinkage approach[J]. Journal of Computer Applications,2010,30(1):78-81.

[10] 黄一鹤.一种基于新的小波阈值函数的图像去噪方法[J].传感器与微系统,2011,30(9):76-78.

HUANG Yihe. A method for image denoising based on new wavelet thresholding function[J]. Transducer and Microsystem Technologies,2011,30(9):76-78.

[11] Zhong J. Image denoising based on wavelets and multifractals for singularity detection and multiscale anisotropic diffusion: US, US 7515763 B1[P]. 2009.

Improved Adaptive New Wavelet Threshold Denoising Algorithm

XIN YuanchaoZHANG Jun’anFANG Zhou

(School of Mechanical and Electronic Engineering, Xi’an Technological University, Xi’an710021)

AbstractExisted in the work of hard and soft threshold denoising algorithm of fuzzy edge and other issues, the distribution characteristics of noise in the image noise are analyzed, a new adaptive denoising algorithm based on least mean square algorithm is proposed. The algorithm is based on hierarchical ideal valve preserving image detail and suppress noise, the level of dimensions adaptive best threshold value is determined, the peak signal to noise ratio is improved. Experimental comparison shows that the new adaptive wavelet threshold denoising algorithm processing image signal to noise ratio are increased by 12%, image denoising effect is obvious.

Key Wordswavelet transform, adaptive denoising, threshold function, signals denoise

收稿日期:2015年12月16日,修回日期:2016年1月24日

作者简介:辛元超,男,硕士,研究方向:图像处理。

中图分类号TP391.41

DOI:10.3969/j.issn.1672-9722.2016.06.035