生物神经网络的建模与仿真
2016-06-29刘剑钊董朝轶冯丽斐
刘剑钊, 董朝轶, 冯丽斐
(1.内蒙古工业大学 电力学院, 呼和浩特 010080; 2. 内蒙古机电控制重点实验室, 呼和浩特 010080)
生物神经网络的建模与仿真
刘剑钊1, 2, 董朝轶1, 2, 冯丽斐1, 2
(1.内蒙古工业大学 电力学院, 呼和浩特 010080; 2. 内蒙古机电控制重点实验室, 呼和浩特 010080)
摘要生物神经网络系统是由许多的神经元之间通过突触相互连接起来,通过突触传递电信号,并且具有相当复杂的非线性网络系统。通过人工构造生物真实性的脉冲神经网络(Spiking Neural Networks, SNN)模型来模拟真实的神经元放电行为。首先,建立基于积分点火(Integrate-and-Fire, IF)机制的SNN模型;然后,确定模型中的参数,并对一个神经元和多个神经元网络进行仿真;最后,对比模型仿真的放电行为和真实神经元放电行为。仿真结果表明:基于IF模型的生物神经网络仿真能较好地逼近真实的生物神经网络。
关键词生物神经网络;脉冲神经网络;积分点火模型;脉冲序列
生物神经网络中最基本的组成单元是神经元,对于单个神经元而言,其功能相当于一个开关作用,而将众多神经元之间通过物理层相互连接,并且相互传递信息,这就构成一个完整和复杂的生物神经网络系统[1-5]。为了更准确地建立生物神经网络系统,SNN的提出对生物神经元生理机制有了很好的诠释。SNN是将真实生物神经元在接受刺激时的放电行为用数学建模的方式描述出来的一种人工构造的生物神经网络,其模拟神经元更加接近实际,并且它也考虑了时间信息的影响。基于人工构造的生物神经网络被称为第3代人工神经网络[6],常见的SNN模型有HH模型[7],IF模型[8],SRM模型[8],Izhikevich模型[9]等,这些模型是在不同的建模精度上对生物神经网络生理机制的一种描述,并可以通过仿真来观测神经元之间的动态特性,本文将通过基于IF模型的SNN来对生物神经网络进行仿真实验。
1IF模型建模
1907年,Lousi Lapicque提出了第一个生物神经网络模型,即IF模型[8]。当时人们并不了解神经元的动作电位形成机制,IF模型的提出展示了神经元的动作电位放电行为。一个典型的生物神经元的放电行为如图1所示。

图 1 IF模型放电行为[8]

IF模型可以看作为一个存在阈值特性的激活系统,具体表现为:当膜电位小于阈值时,神经元不会产生动作电位,且膜电位会随着指数衰减到静息值;而当膜电位大于或者等于阈值时,神经元立即产生兴奋,即发放脉冲,伴随动作电位的传导。IF模型非常直观地描述了神经元的膜电位和其输入电流之间的关系。当神经元未产生动作电位时,IF模型的一阶微分方程如下表示:
(1)
可简化为:
(2)
其中τm为膜电压时间常量,Cm为膜电容,Rm为膜电阻,Em为静息电位,I(t)为各个突触前神经元放电行为势所产的突触电流之和。I(t)与单个突触的连接强度有关,假设wij表示为第j个突触前神经元对突触后神经元i的权重,那么总的输入电流如下表示:
(3)
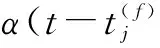
t(f):V(t(f))=ϑ
(4)
并且,当发放脉冲之后,膜电位V立刻重设为复位值Vr,且Vr<ϑ,
(5)
神经元膜电位复位之后将进入一个时间约为2 ms绝对不应期,处于绝对不应期时刻的神经元有任何刺激时,不再积累膜电势。绝对不应期时刻过后,神经元则可以重新按式(1)积累膜电势,进入下一轮的电压积累、放电的动态特性。
2仿真结果
给出重要参数初始化数据Em=-70 mV,ϑ=-55 mV,Vr=-75 mV,Rm=10 kΩ,τm=10 ms。
2.1 单神经元脉冲动态特性
在100 ms~400 ms内,I= 1.0 μA,仿真如图2所示,可以看到神经元膜电位最高为-60 mV,并没有达到阈值-55mV,所以不会产生脉冲输出。
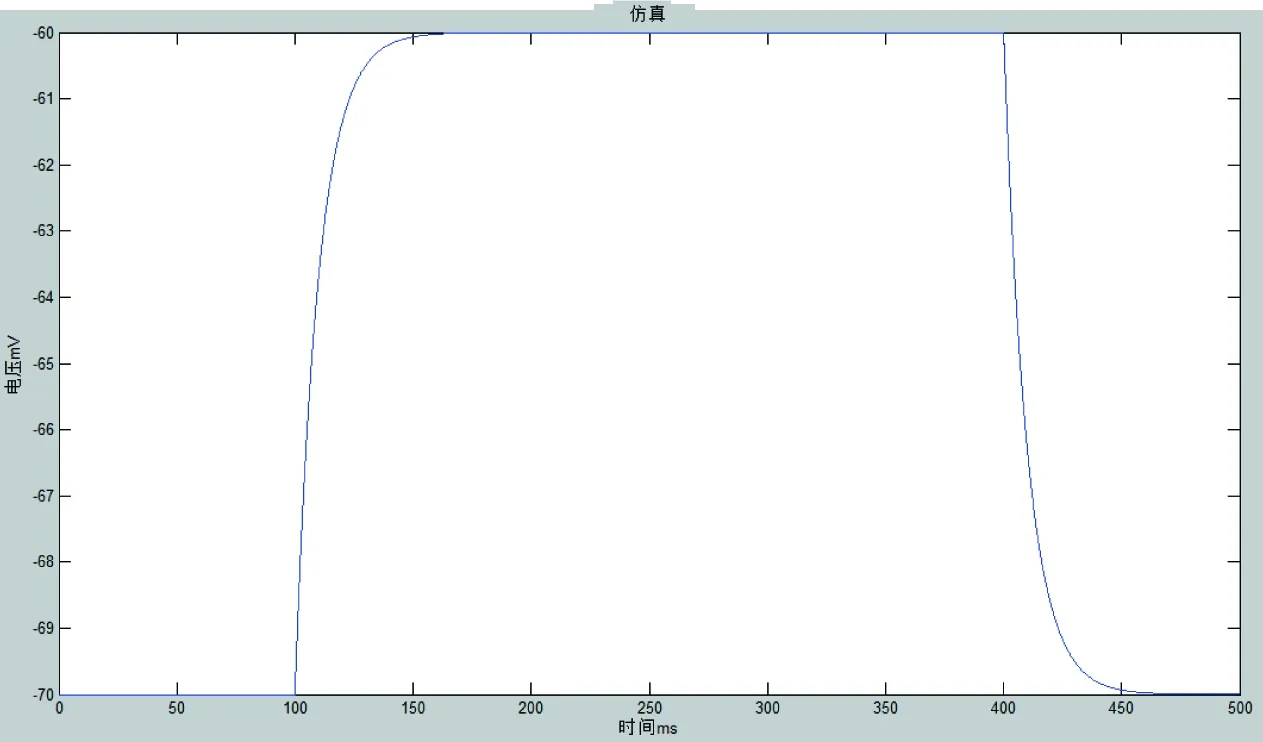
图 2 I = 1.0 μA时仿真结果
当I= 1.55 μA时,仿真如图3所示,神经元膜电位达到了阈值-55 mV,所以立即产生脉冲序列,并且达到峰值电压20 mV,之后迅速重置为复位电压-75 mV,经过2 ms的绝对不应期,开始新一轮的电压积累点火。
当I= 2.0 μA时,仿真如图4所示,通过加大电流,仿真得出脉冲点火频率也随着增大了。
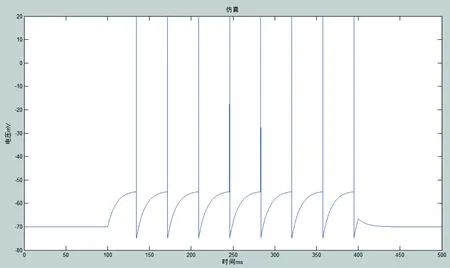
图 3 I = 1.55 μA时仿真结果

图 4 I = 2.0 μA时仿真结果
2.2多神经元脉冲网络
下面以10个神经元来进行仿真,其中每个神经元的输入电流不再是常量,而是随机高斯白噪声。如图5所示,神经元不再以固定的频率产生脉冲序列,而是随着随机的噪声电流也呈现了不规则的脉冲序列。

图 5 10个神经元网络仿真结果
3结论
通过上述建模仿真结果可知,IF模型是一种简单,并且能够较准确地模拟真实生物神经元网络的动态特性。未来可以通过改变神经元之间的连接强度产生的脉冲序列,运用脉冲序列对网络连接结构进行反向辨识[10,11],然后通过生物神经网络电生理实验,如多电极阵列(Multi-electrode Array, MEA)可获得体外培养网络的多通道脉冲响应数据[12-14],将真实的生物神经网络数据运用到模型上辨识网络动态结构,这将会对生理、病理上有更深地理解和认识。
参考文献:
[1]寿天德. 神经生物学[M]. 北京:高等教育出版社, 2013.
[2]STERRATT D, GRAHAM B, GILLIES A, et al. Principles of computational modelling in neuroscience[M]. Cambridge: Cambridge University Press, 2011.
[3]陆启韶, 刘深泉, 刘 锋, 等. 生物神经网络系统动力学与功能研究[J]. 力学进展, 2008, 38(6):766-793.
[4]郑鸿宇, 罗晓曙, 吴 雷. 变权小世界生物神经网络的兴奋及优化特性[J]. 物理学报, 2008, 57(6):3380-3384.
[5]陈后金, 袁保宗. 生物神经网络仿真中数据表达和并行处理[J]. 系统仿真学报, 2003, 15(5):649-652.
[6]MAASS W. Networks of spiking neurons: The third generation of neural network models[J]. Neural Networks, 1997, 10(4):1659-1671.
[7]HODGKIN A L, HUXLEY A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. J Physiol, 1952, 117(4):500-544.
[8]GERSTENER W, KISTLER W. Spiking neuron models[M]. Cambridge University Press, 2002.
[9]IZHIKEVICH E M. Which model to use for cortical spiking neurons?" Neural Networks[J]. IEEE Trans Neural Netw, 2004, 15(5):1063-1070.
[10]DONG C Y, SHIN D, JOO S, et al. Identification of feedback loops in neural networks based on multi-stepGrangercausality[J]. Bioinformatics, 2012, 28(16):2146-2153.
[11]ZHANG X, ZHAO X M, HE K, et al. Inferring gene regulatory networks from gene expression data by pc-algorithm based on conditional mutual information[J]. Bioinformatics, 2012, 28(1):98-104.
[12]MAROM S, SHAHAF G. Development, learning and memory in large random networks of cortical neurons: lessons beyond anatomy[J]. Quarterly Reviews of Biophysics, 2002, 35(1):63-87.
[13]WEI W, SONG Y, SHI W, et al. A high sensitivity MEA probe for measuring real time rat brain glucose flux[J]. Biosensors & Bioelectronics, 2014, 55:66-71.
[14]ASAKURA K, HAYASHI S, OJIMA A, et al. Improvement of acquisition and analysis methods in multi-electrode array experiments with iPS cell-derived cardiomyocytes[J]. Journal of Pharmacological & Toxicological Methods, 2015, 75:17-26.
Modeling and simulation of biological neural networks
LIU Jian-zhao1, 2, DONG Chao-yi1, 2, FENG Li-fei1, 2
(1. College of Electric Power, Inner Mongolia University of Technology, Hohhot 010080;2. The Key Laboratory of Electromechanical Control, Inner Mongolia, Hohhot 010080, China)
AbstractBiological neural networks system is composed of a number of neurons through synapses between each other, transmitting electrical signals through the synapse, and has a very complex nonlinear network system. In this paper, the Spiking Neural Networks (SNN) model is constructed to simulate the real neuron discharge behavior. First, the SNN model is established based on the Integrate-and-Fire (IF) mechanism. Then, the parameters of the model are determined, and then the simulation of a neuron and a plurality of neurons is carried out. Finally, compare between model simulation and real neuron discharge behavior. The simulation result shows that the biological neural networks based on the IF model can be used to approximate the real biological neural networks.
Key wordsbiological neural networks; spiking neural networks; IF model; spiking series
收稿日期:2015-09-02;修回日期:2015-09-30
基金项目:国家自然科学基金地区基金项目(61364018);教育部留学回国人员科研启动基金(第45批);内蒙古自治区高等学校“青年科技英才计划”-青年科技领军人才;内蒙古工业大学青年学术骨干项目
作者简介:刘剑钊,硕士,研究方向为生物信息处理,E-mail:liuxxxxliu@qq.com; 通信作者:董朝轶,教授,博士,研究方向为系统生物学、飞行器控制,E-mail: dongchaoyi@hotmail.com。
中图分类号Q6-33
文献标识码B
文章编号2095-1736(2016)03-0104-03
doi∶10.3969/j.issn.2095-1736.2016.03.104
