基于高性能磁链算法的永磁同步电动机无位置传感器控制

李　彪　李黎川

(西安交通大学电气工程学院　西安　710049)

基于高性能磁链算法的永磁同步电动机无位置传感器控制

李彪李黎川

(西安交通大学电气工程学院西安710049)

摘要准确的磁链辨识是基于磁链观测法永磁同步电动机无位置传感器控制的关键，传统电压型磁链辨识算法消除了纯积分存在漂移问题，对圆形磁场的磁链可以准确辨识，但对实际中电机内普遍存在的椭圆形磁场的磁链辨识时存在稳态幅值和相位误差。分析了椭圆形磁场时磁链矢量与反电动势矢量的空间关系。对传统算法辨识椭圆形磁链的误差进行了分析，提出一种改进的新型磁链算法。改进后的新算法运算量与传统算法相当，但对圆形与椭圆形磁场的磁链均能准确辨识。将新算法应用于一台表贴式永磁同步电动机无位置传感器控制系统的转子位置估算，仿真证明，在稳态及转速突变时新算法均具有良好的位置和转速跟踪效果。利用数字信号处理器TMS320F2812DSP对其进行了数字化实现。实验结果表明，在中高速范围内，调速系统在稳态与电机转速突变时具有良好的动静态特性，但在低速区会出现系统不稳定。仿真与实验证明了新算法的有效性和实际可应用性。

关键词：磁链辨识椭圆形旋转磁场永磁同步电动机无位置传感器控制

0引言

永磁同步电动机因具有效率高、功率因数高以及控制简单等优点，在工业中得到了广泛应用。对永磁同步电动机进行精确控制需要转子的位置和转速信息。但传统机械式传感器的使用会增加系统的成本和尺寸，使系统易受干扰，且不适于恶劣的工作环境。因此无位置传感器控制技术得到了广泛研究。基于永磁同步电动机凸极效应的高频注入法可应用于较宽的速度范围，特别是在低速时可取得相对较好的效果，但该方法需要电机具有凸极效应。磁链观测法根据永磁同步电动机的电磁关系，通过电机的定子绕组反电动势来实时辨识定子磁链进而获得转子位置信息，不需要凸极效应，且简单、高效、易实现，从而在工业中获得了广泛应用。但电压型磁链算法中存在的纯积分环节会在辨识的磁链中引入初始相位误差和直流偏置误差，从而产生积分漂移，导致转矩脉动，影响系统运行稳定性。

为了解决电压型磁链算法中纯积分环节存在的问题，常用一阶低通滤波器(LPF)来代替纯积分环节，由于移除了纯积分在原点处的极点，从而可解决漂移问题，但又引入稳态误差，尤其当电机运行在低通滤波器截止频率以下时，电机控制准确度很低。文献[1-6]采用一阶低通滤波器代替纯积分，用一个补偿环节来补偿稳态幅值和相位误差。文献[4，7]指出交换低通滤波环节与补偿环节的相对位置，可增强动态过程中磁链辨识准确度。文献[8]采用一阶高通滤波器(HPF)代替纯积分有效解决了输出中直流偏置问题，用一个坐标变换环节来补偿稳态幅值和相位误差，但高通滤波器对系统中高频干扰抑制力较弱，不利于系统稳定。文献[9-12]采用一阶低通滤波器与一阶高通滤波器串联代替纯积分用于消除初始相位误差与直流偏置误差，再用串联的补偿环节补偿稳态幅值和相位误差。文献[13]采用带通滤波器(BPF)代替纯积分环节，并对辨识结果稳态时的幅值和相位误差进行了补偿。文献[14]采用五阶低通滤波器串联一阶高通滤波器和一个逻辑转换模块的算法，有效消除了积分漂移，同时抑制了系统中的高频干扰。

上述算法中关于滤波器截止频率选取，相对于截止频率取某一固定值，文献[3-5，8-11，14]中采用截止频率是同步角频率某一倍数的可编程滤波器，从而使算法在低速时兼顾了对磁链中直流偏置抑制的能力与动态过程中磁链辨识的准确度。关于稳态时幅值和相位误差的补偿，文献[2-6，11，13]中的补偿环节采用旋转空间矢量的方法；文献[1，7，9，10，12，14]中补偿环节基于相关时间相量间的关系实现；文献[8]中补偿环节通过坐标变换实现。通过分析时间相量移相、空间矢量旋转及坐标变换之间的关系可知，上述补偿方法本质相通。文献[6]中还引入定子磁链的电流模型和电压模型之间的误差对定子感应电动势进行补偿。文献[15]用低通滤波器代替纯积分，并用另一个低通滤波器进行稳态幅值相位的补偿，两个低通滤波器截止频率要求严格，需满足一定关系。同时低速时无法使两个滤波器时间常数同时较低，大的时间常数导致输入变化时又出现漂移问题。

传统的滤波器串联补偿环节的这类算法[1-14，16]，实现简单，可以在较宽的转速范围内实现磁链准确辨识。但对这类算法分析发现，稳态时算法辨识磁链准确性必须基于以下条件之一：①在时域α、β两相对称；②在空间磁链矢量滞后于反电动势矢量π/2(电机反转时则超前π/2)。分析可知这两个条件只在圆形磁场时成立。

通常电机本体设计和实时控制都期望电机中的磁场呈圆形。而实际中，由于电机电阻和电感参数的不对称、逆变器电压-电流的非线性特性、逆变器开关量所加死区的影响、各相电流检测电路及调理电路的不对称、AD采样转换电路的不对称、负载不对称等各种因素的影响以及调速系统动态调整过程中，电机磁场都会呈椭圆形。此时前述算法就不再有效，图1为α、β两相反电动势存在5%幅值误差和10%相位误差时(具体参数见本文仿真部分)传统典型算法稳态辨识结果，存在明显稳态误差。

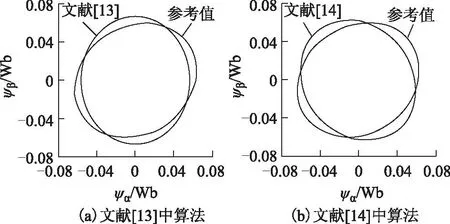
图1　椭圆形磁链时传统磁链算法辨识结果Fig.1　Estimation results of traditional flux algorithms when elliptical flux

基于滤波器加补偿环节的这类传统电压型磁链算法，结构简单，有利于工业实际应用，但算法基于圆形磁场，从而对普遍存在的椭圆形磁场磁链辨识存在稳态误差。本文首先分析了椭圆形磁场时，磁链矢量与反电动势矢量的空间关系，然后对传统算法辨识椭圆形磁链时的误差进行了分析，并对传统算法进行了改进。改进后的新算法对圆形、椭圆形磁链均能准确辨识，同时给出了椭圆形磁链的逆时针圆形旋转分量与顺时针圆形旋转分量的辨识算法。将改进的新型磁链算法应用于永磁同步电动机无位置传感器调速系统的转子位置估算。通过仿真与实验证明了新算法的有效性和实用性。

1新算法原理

在静止两相αβ坐标系下，交流电机电压模型磁链表达式为

(1)

式中，ψα,β、eα,β、vα,β、iα,β分别为磁链、反电动势、端电压与电流的α、β轴分量；Rs为绕组电阻。

为方便理解，本文采用空间矢量作为数学工具对新算法进行推导描述。

1.1磁链矢量与反电动势矢量空间关系

圆形磁场是椭圆形磁场的特例，本文将椭圆形磁场作为一般情况推导空间磁链矢量与反电动势矢量的关系。三相不对称时磁场将呈椭圆形，根据对称分量法可将一组不对称的三相某物理量分解成正序、负序、零序三组对称分量。零序分量对空间矢量贡献为零，因此只考虑各相正序与负序分量[17]。从三相自然坐标系变换到两相静止αβ坐标后，设有两相量

(2)

(3)

(4)

=X++X-

(5)

由式(5)可知，椭圆形矢量由两个转速相等、转向相反的圆形矢量分量合成，其中逆时针旋转分量X+的实部与虚部对应于时域相量正序分量的α、β相分量；顺时针旋转分量X-的实部与虚部对应于时域相量负序分量的α、β相分量。

若在时域，对各相量滞后相移φ，如式(6)所示。

(6)

将式(6)代入式(5)可得

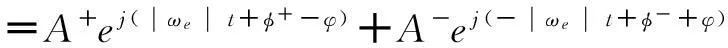
=X+e-jφ+X-ejφ

(7)

由式(7)可知，当时域各相量相位滞后相移φ，对应空间矢量的逆时针旋转分量将在空间顺时针旋转φ角度，顺时针旋转分量将在空间逆时针旋转φ角度。

(8)

1.2改进的新型磁链算法

对于圆形磁场，根据文献[5]中总结的传统磁链辨识思想，用低通滤波器代替纯积分，调整增益补偿稳态幅值误差，再通过旋转矢量补偿稳态相位误差。图2a为文献[5]中算法框图，由图所示经过补偿环节的矢量旋转后，无论电机正转或反转，磁链矢量在空间均滞后反电动势矢量π/2。经本文分析可知，电机正转时，磁链矢量滞后反电动势矢量π/2；电机反转时，磁链矢量超前反电动势矢量π/2。因此，对于圆形磁场正确的矢量旋转补偿环节框图应为图2b所示。图2b所示传统磁链算法推导均基于圆形磁链，对椭圆形磁链辨识则存在稳态误差。

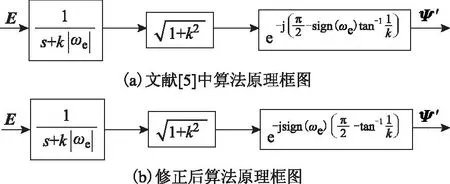
图2　传统磁链算法原理框图Fig.2　Block diagram of traditional flux algorithm

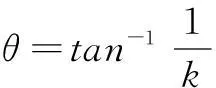
(9)

将式(9)展开整理可得到

(10)

相对于式(8)所示磁链实际值Ψ，Ψ ′存在的误差为

(11)

为了准确辨识椭圆形磁链，对图2b所示传统算法进行改进。

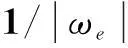
(12)

首先推导ωe≥0，即电机逆时针旋转时的情况。

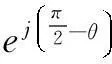
(13)

再根据矢量关系Ψ=2Ψ+-(Ψ+-Ψ-)，可得到ωe≥0时椭圆形磁链算法

(14)

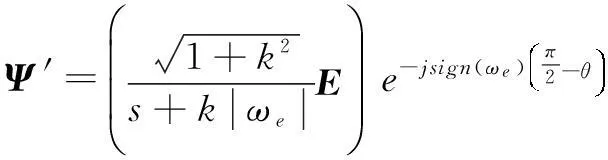
(15)

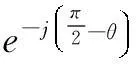
(16)

再根据矢量关系Ψ=2Ψ-+(Ψ+-Ψ-)，可得到ωe<0时椭圆形磁链算法

(17)

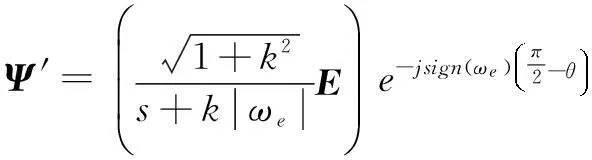
(18)

式(15)所示电机逆时针旋转(ωe≥0)的磁链算法与式(18)所示电机顺时针旋转(ωe<0)的磁链算法可统一表达形式仍如式(18)所示，所以改进后新磁链算法不需要判断电机转向。新算法两相独立辨识磁链，不存在耦合，运算量与原算法相当。

由式(12)和式(18)可得椭圆形磁链的逆时针旋转分量与顺时针旋转分量辨识算法

(19)

(20)

改进后的新磁链算法原理框图如图3a所示，椭圆形磁链的两个圆形分量的辨识算法原理框图如图3b、图3c所示。

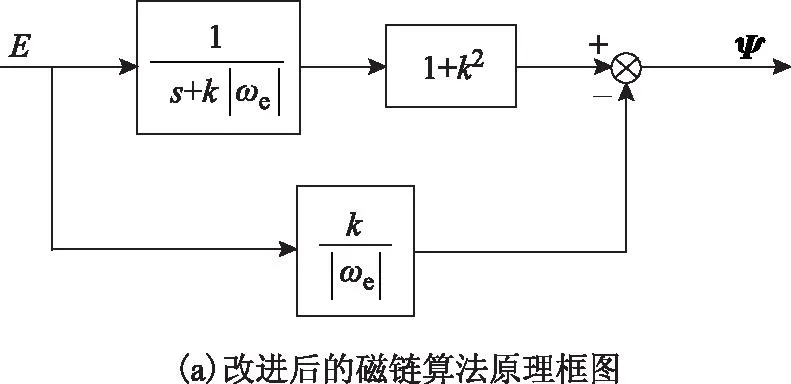
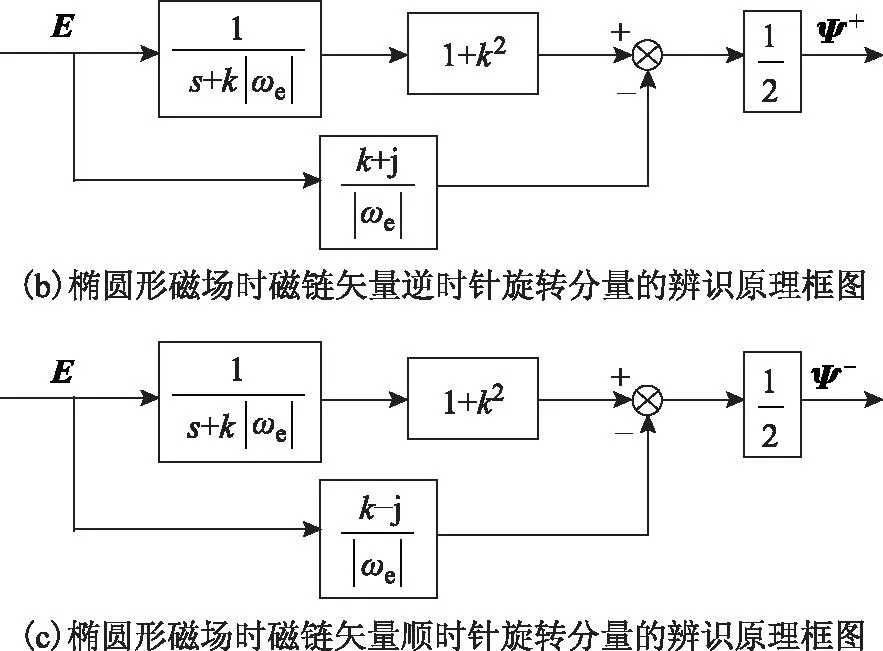
图3　新磁链算法原理框图Fig.3　Block diagram of the new flux algorithms

2仿真与实验

为了验证改进后新磁链算法的有效性，在Matlab/Simulink中进行了离散系统仿真，采样频率为12 kHz，低通滤波器截止频率系数k=1.5。

图4a为仿真所加反电动势波形。从0～0.2 s，反电动势幅值从0 V线性增加到7.97 V，频率为20 Hz。从0.2～0.3 s，反电动势幅值和频率保持不变。在0.3 s反电动势幅值跃变为15.94 V，频率跃变为40 Hz。从0～0.5 s，反电动势均叠加了大小为幅值1%的直流偏置。新算法辨识结果如图4b所示。从仿真结果可知，新算法有效解决了积分漂移问题，同时不引入稳态误差，具有良好的动静态性能。

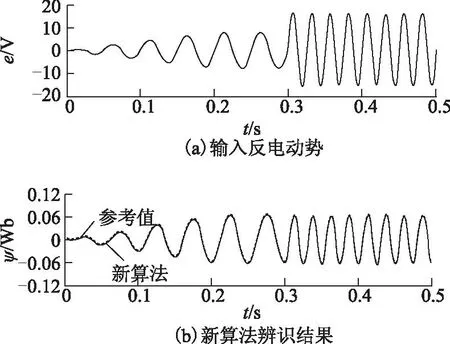
图4　新磁链算法辨识结果Fig.4　Result of the new flux algorithm

图5为两相反电动势不对称、磁链矢量轨迹为椭圆形时，不同算法辨识的稳态仿真结果。反电动势频率为20 Hz，α相幅值为7.97 V，β相幅值为α相的0.95倍，β相反电动势相位滞后于α相9π/20，同时两相反电动势均叠加了大小为各自幅值1%的直流偏置。图5a为纯积分法辨识结果，存在明显的漂移。图5b为原算法与改进后新算法磁链辨识结果，原算法与新算法均消除了积分漂移，但原算法相对参考值存在明显的稳态误差，而改进后新算法不存在稳态误差。文献[13，14]中算法辨识结果如图1所示，消除了漂移，但存在稳态误差。图5c、图5d为椭圆形磁链的逆时针旋转分量与顺时针旋转分量稳态辨识结果。

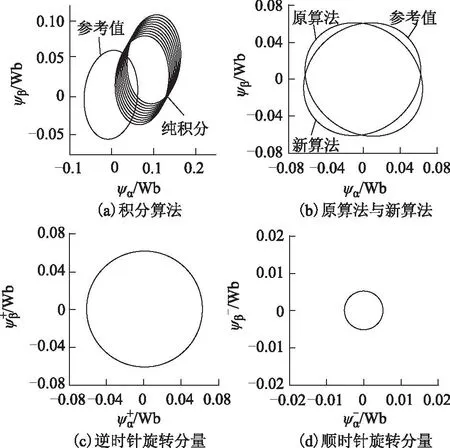
图5　椭圆形磁链时不同磁链算法辨识结果比较Fig.5　Comparison of different flux estimation algorithms when elliptical flux

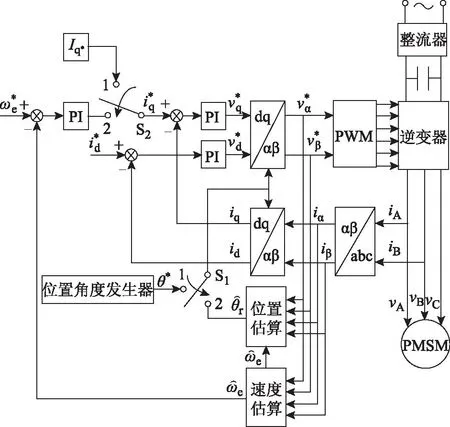
图6　永磁同步电动机无位置传感器矢量控制系统框图Fig.6　Position sensorless vector control of PMSM schematic diagram

将本文磁链算法应用于一台表贴式永磁同步电动机无位置传感器调速系统的转子位置估算。矢量系统控制框图如图6所示。系统采用速度-电流双闭环矢量控制，电流环采用id=0控制策略。电机电流采用霍尔传感器实时检测。系统控制周期，电流采样及调节周期，磁链、位置与速度的估算周期均为Ts=83.3 μs，速度环调节周期为10Ts。电流环与速度环均采用PI调节器[18]。实验平台实物图如图7所示，逆变器主电路由MOSFET构成，主控芯片采用TI公司的TMS320F2812 DSP，片内集成有A-D转换模块。电机参数见附录。

图7　实验平台实物图Fig.7　Experimental platform

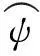
(21)

(22)

(23)

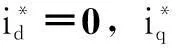
为了验证基于新磁链算法的转子位置估算算法的效果，图8为永磁电机处于无位置传感器控制运行状态，当参考转速在35 s从450 r/min跃变到1 000 r/min及在37.5 s从1 000 r/min跃变到450 r/min时，转子位置估算值与实际值对比仿真结果。图中转子位置空间角度为电角度。由图可看到，稳态时，位置估算算法可以很好地估算转子位置，误差在2.4°(电角度)以内；在转速突变时，转子位置估算会出现较大误差，但会在一个电周期内收敛到实际值。

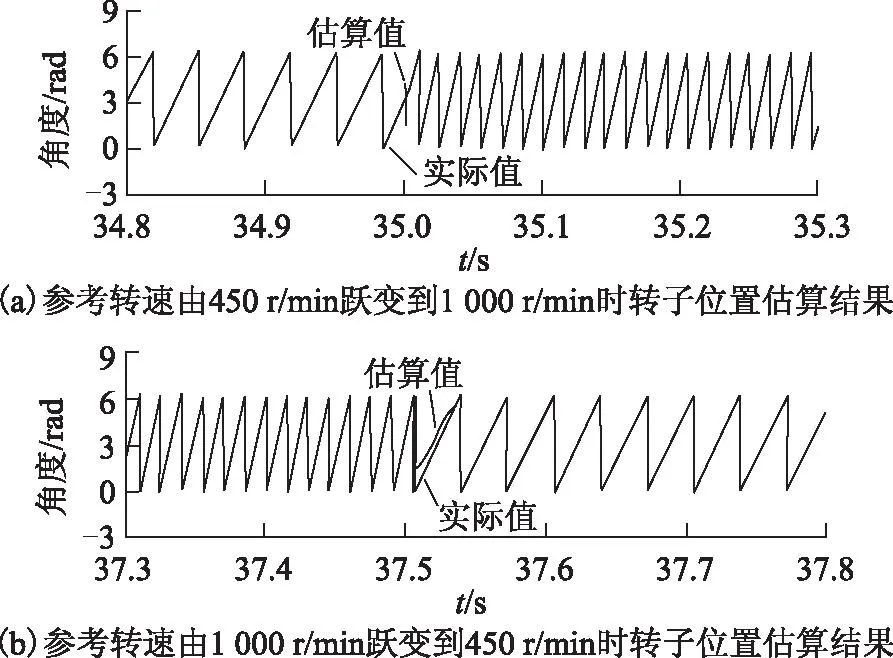
图8　参考转速在450 r/min与1 000 r/min之间跃变时，转子位置估算结果Fig.8　Rotor position estimated when the reference speed is step changed between 450-1 000 r/min

为了验证转速估算算法对转子实际转速的追踪性能，图9为永磁电机处于无位置传感器控制运行状态，当参考转速在35 s从450 r/min跃变到1 000 r/min及在37.5 s从1 000 r/min跃变到450 r/min时，转速估算值与实际值对比仿真结果。由图可看到，稳态时，转速估算算法可以很好地追踪实际转速；在转速突变时，由于对用于估算转速的反电动势进行了低通滤波，从而使转速动态追踪存在较小的滞后与误差。

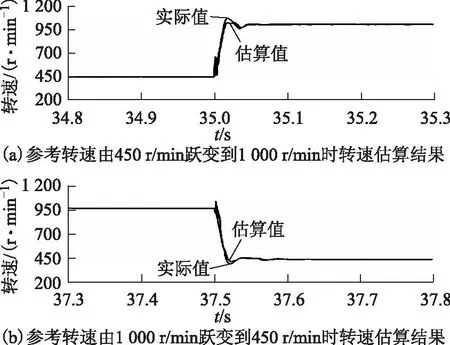
图9　参考转速在450 r/min与1 000 r/min之间跃变时，转速估算结果Fig.9　Speed estimated when the reference speed is step changed between 450-1 000 r/min

实验时，为了用示波器观察相关变量，将要输出的数据作为调制波，通过DSP的PWM算法模块以一系列脉冲输出，经过RC低通滤波器后，供示波器观察。

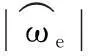
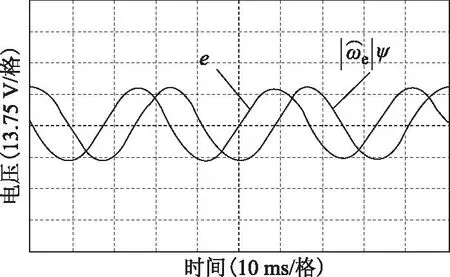
图10　转速为450 r/min时，反电动势与新算法辨识的磁链波形Fig.10　EMF and flux estimated by the new algorithms at n=450 r/min

图11为当电机参考转速在450 r/min与1 000 r/min之间跃变时，电机转速估算值与新算法辨识的定子磁链实验波形。由图可见，当电机转速突变时，新算法具有良好的磁链辨识效果，从而使系统具有良好的动态性能。

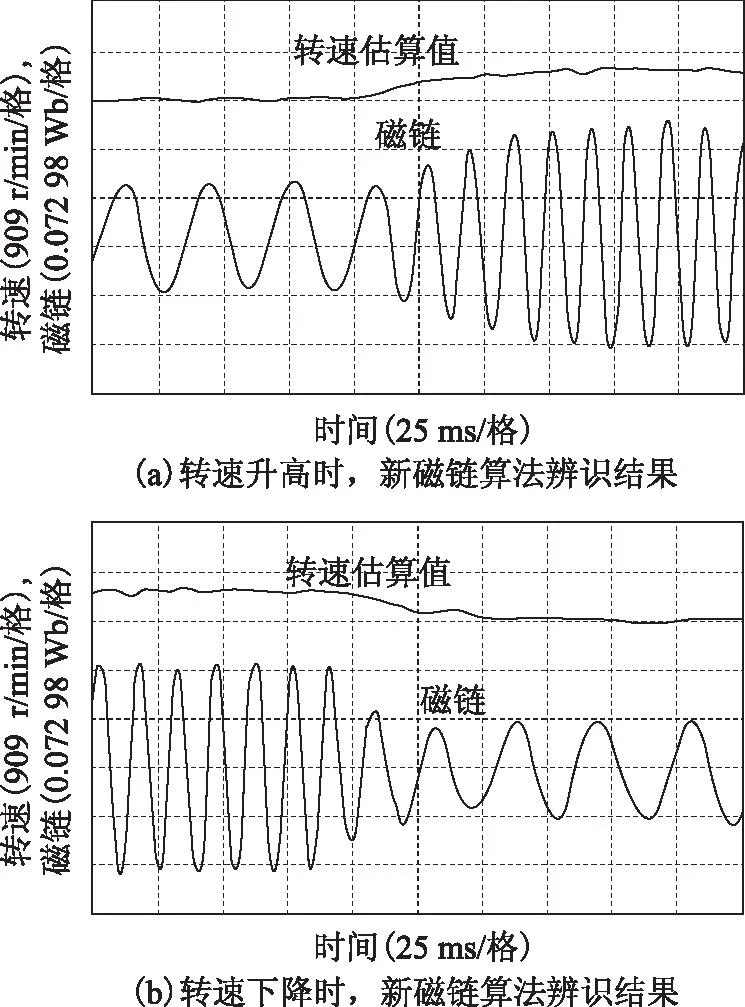
图11　转速在450r/min与1 000 r/min跃变时，新磁链算法辨识结果波形Fig.11　Flux estimated by the new algorithm when the speed is step changed between 450-1 000 r/min

图12为当电机参考转速在450 r/min与1 000 r/min之间跃变时，电机转速估算值与基于新磁链算法估算的转子位置角度实验波形。

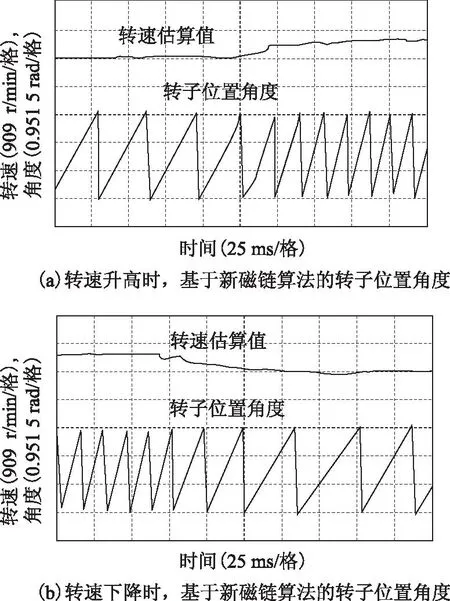
图12　转速在450 r/min与1 000 r/min之间跃变时，基于新磁链算法的转子位置角度波形Fig.12　Rotor position estimated based on the new flux algorithmwhen the speed is step changed between 450-1 000 r/min

3结论

1)基于磁链观测法的永磁同步电动机无位置传感器控制系统，简单高效，易于实现，不需要电机具有凸极性，但电压模型磁链算法中纯积分存在漂移问题。传统的滤波器串联补偿环节的磁链算法，基于α、β两相对称或空间磁链矢量与反电动势矢量正交，所以只适合圆形磁场，而对实际中普遍存在的椭圆形磁场磁链辨识则存在稳态误差。

2)分析了磁链矢量与反电动势矢量的空间关系后，在传统磁链算法基础上提出一种改进的新型磁链算法。新算法运算量与传统算法相当，但对圆形和椭圆形磁场磁链均能准确辨识。同时得到了椭圆形磁场磁链的逆时针旋转分量与顺时针旋转分量的辨识算法。新磁链算法编程实现简单，运算量小，适合于工业实时控制系统。

3)将新磁链算法应用于一台表贴式永磁同步电机无位置传感器调速系统中的转子位置估算。由于本文磁链与转速的估算均基于感应的反电动势信号，在低速区，因为无法获取足够大的反电动势信号而会出现磁链、位置及转速估算不准确。实验中发现，在低速区(额定转速10%以下)转子位置估算会出现较大的误差波动，系统会出现不稳定甚至失步；而在中高速区运行时，系统在稳态与电机转速突变时具有良好的动、静态特性。

附录

仿真与实验电机参数：

额定功率PN=0.4 kW；额定电流IN=2.5 A；额定转速nN=3 000 r/min；直、交轴电感Ld=Lq=5.55 mH；定子电阻Rs=1.4 Ω；极对数p=4；永磁体磁链ψf=0.063 417 9 Wb。

参考文献

[1]Idris N R N，Yatim A H M.An improved stator flux estimation in steady-state operation for direct torque control of induction machines[J].IEEE Transactions on Industry Applications，2002，38(1)：110-116.

[2]Li Yong，Huang Wenxin，Hu Yuwen.A low cost implementation of stator-flux-oriented induction motor drive[C]//Proceedings of the Eighth International Conference on Electrical Machines and Systems，Piscataway，NJ，2005：1534-1538.

[3]Shin M H，Hyun D S，Cho S B，et al.An improved stator flux estimation for speed sensorless stator flux orientation control of induction motors[J].IEEE Transactions on Power Electronics，2000，15(2)：312-318.

[4]Hinkkanen M，Luomi J.Modified integrator for voltage model flux estimation of induction motors[J].IEEE Transactions on Industrial Electronics，2003，50(4)：818-820.

[5]Comanescu M，Xu L.An improved flux observer based on PLL frequency estimator for sensorless vector control of induction motors[J].IEEE Transactions on Industrial Electronics，2006，53(1)：50-56.

[6]陈振锋，钟彦儒，李洁，等.基于改进磁链观测器的感应电机转速辨识[J].电工技术学报，2012，27(4)：42-47.

Chen Zhenfeng，Zhong Yanru，Li Jie，et al.Speed identification for induction motor based on improved flux observer[J].Transactions of China Electrotechnical Society，2012，27(4)：42-47.

[7]何志明，廖勇，何大为.定子磁链观测器低通滤波器的改进[J].中国电机工程学报，2008，28(18)：61-65.

He Zhiming，Liao Yong，He Dawei.Improvement of low-pass filter algorithm for stator flux estimator[J].Proceedings of the CSEE，2008，28(18)： 61-65.

[8]王宇，邓智泉，王晓琳.一种新颖的电机磁链辨识算法[J].中国电机工程学报，2007，27(6)：39-44.

Wang Yu，Deng Zhiquan，Wang Xiaolin.A novel algorithm of motor flux estimation[J].Proceedings of the CSEE，2007，27(6)：39-44.

[9]张星，瞿文龙，陆海峰.一种能消除直流偏置和稳态误差的电压型磁链观测器[J].电工电能新技术，2006，25(1)：39-43.

Zhang Xing，Qu Wenlong，Lu Haifeng.Method for elimination of DC offset and steady state error for voltage module flux observer[J].Advanced Technology of Electrical Engineering and Energy，2006，25(1)：39-43.

[10]李彪，刘新正，李黎川.具有低通滤波的改进电压模型磁链观测器[J].西安交通大学学报，2009，43(12)：91-95.

Li Biao，Liu Xinzheng，Li Lichuan.Modified algorithm for voltage module flux estimation with low pass filter[J].Journal of Xi’an Jiaotong University，2009，43(12)：91-95.

[11]孙大南，林文立，刁利军，等.改进型感应电机电压模型磁链观测器设计[J].北京交通大学学报，2011，35(2)：94-98.

Sun Danan，Lin Wenli，Diao Lijun，et al.Improved voltage model flux observer design of induction machine[J].Journal of Beijing Jiaotong University，2011，35(2)：94-98.

[12]史黎明，王珂，李耀华.基于改进磁链观测器的直线异步电动机直接牵引力控制[J].电工技术学报，2008，23(9)：45-50.

Shi Liming，Wang Ke，Li Yaohua.Direct thrust control of linear induction motor based on improved flux observer[J].Transactions of China Electrotechnical Society，2008，23(9)：45-50.

[13]李红，罗裕，韩邦成，等.带通滤波器法电压积分型定子磁链观测器[J].电机与控制学报，2013，17(9)： 8-16.

Li Hong，Luo Yu，Han Bangcheng，et al.Voltage integral model for stator flux estimator based on band-pass filter[J].Electric Machines and Control，2013，17(9)：8-16.

[14]Wang Yu，Deng Zhiquan.An integration algorithm for stator flux estimation of a direct-torque-controlled electrical excitation flux-switching generator[J].IEEE Transactions on Energy Conversion，2012，27(2)：411-420.

[15]文晓燕，郑琼林，韦克康，等.带零漂补偿和定子电阻自校正的磁链观测器[J].中国电机工程学报，2011，31(12)：102-107.

Wen Xiaoyan，Zheng Qionglin，Wei Kekang，et al.Flux observer with offset compensation and stator resistance self-correction[J].Proceedings of the CSEE，2011，31(12)：102-107.

[16]何志明，廖勇，向大为.基于改进层叠式可编程低通滤波器的磁链观测方法[J].电工技术学报，2008，23(4)：53-58.

He Zhiming，Liao Yong，Xiang Dawei.A new flux estimation method based on modified programmable cascaded low-pass filter[J].Transactions of China Electrotechnical Society，2008，23(4)：53-58.

[17]张桂斌，徐政，王广柱.基于空间矢量的基波正序、负序分量及谐波分量的实时检测方法[J].中国电机工程学报，2001，21(10)：1-5.

Zhang Guibin，Xu Zheng，Wang Guangzhu.Study and simulation of real-time detecting method for fundamental positive sequence，negative sequence components and harmonic components based on space vector[J].Proceedings of the CSEE，2001，21(10)：1-5.

[18]王莉娜，朱鸿悦，杨宗军.永磁同步电动机调速系统PI控制器参数整定方法[J].电工技术学报，2014，29(5)：104-117.

Wang Lina，Zhu Hongyue，Yang Zongjun.Tuning method for PI controllers of PMSM driving system[J].Transactions of China Electrotechnical Society，2014，29(5)：104-117.

[19]王子辉，叶云岳.反电势算法的永磁同步电机无位置传感器自启动过程[J].电机与控制学报，2011，15(10)：36-42.

Wang Zihui，Ye Yunyue.Research on self-startup states process of back-EMF based sensorless vector control of PMSM[J].Electric Machines and Control，2011，15(10)：36-42.

[20]黄科元，周李泽，周滔滔，等.一种增强可靠性的永磁同步电机初始角检测[J].电工技术学报，2015，30(1)：45-51.

Huang Keyuan，Zhou Lize，Zhou Taotao，et al.An enhanced reliability method for initial angle detection on surface mounted permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society，2015，30(1)：45-51.

[21]鲁家栋，刘景林，卫丽超.永磁同步电机转子初始位置检测方法[J].电工技术学报，2015，30(7)：105-111.

Lu Jiadong，Liu Jinglin，Wei Lichao.Estimation of the initial rotor position for permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society，2015，30(7)：105-111.

Position Sensorless Control of Permanent Magnet Synchronous Motor Based on High Performance Flux Estimation Algorithm

Li BiaoLi Lichuan

(School of Electrical EngineeringXi’an Jiaotong UniversityXi’an710049China)

AbstractAccurate flux estimation is the key to position sensorless control of permanent magnet synchronous motor based on flux observation.Traditional flux estimation algorithms,based on the voltage model,can effectively solve the problems associated with a pure integrator,and can estimate the flux exactly in the round rotating magnetic field situation.But in real motors,the elliptical rotating magnetic field will introduce magnitude and phase errors in the steady state.The relationship between the back electromotive force(EMF)vector and the flux vector in the elliptical rotating magnetic field is analyzed.After an error analysis of the traditional flux estimation algorithms in the elliptical rotating magnetic field,an improved flux estimation algorithm is proposed.The new algorithm can estimate the flux exactly either in the round rotating magnetic field or in the elliptical rotating magnetic field with similar computational complexity to traditional algorithms.The new algorithm has been used for rotor position estimation in position sensorless vector control of a surfacermounted permanent magnet synchronous motor.Simulation results show that,the new algorithm has good speed and position tracking effect either in the steady state or when the motor speed has step changes.The experiment is implemented using the digital signal processor TMS320F2812DSP.Experimental results show that,in the medium and high speed region,the speed control system has good steady state performance as well as dynamic performance when the motor speed has step changes.But it will be unstable in the lowrspeed region.Both simulation and experiment results show the validity and applicability of the new algorithm.

Keywords：Flux estimation，elliptical rotating magnetic field，permanent magnet synchronous motor，position sensorless control

收稿日期2015-02-13改稿日期2015-06-12

作者简介E-mail：biao.li@stu.xjtu.edu.cn(通信作者) E-mail：lcli@mail.xjtu.edu.cn

中图分类号：TM359

李彪男，1983年生，博士研究生，研究方向为永磁同步电机无位置传感器控制。

李黎川男，1963年生，博士，教授，博士生导师，研究方向为磁悬浮轴承与精密运动控制等。